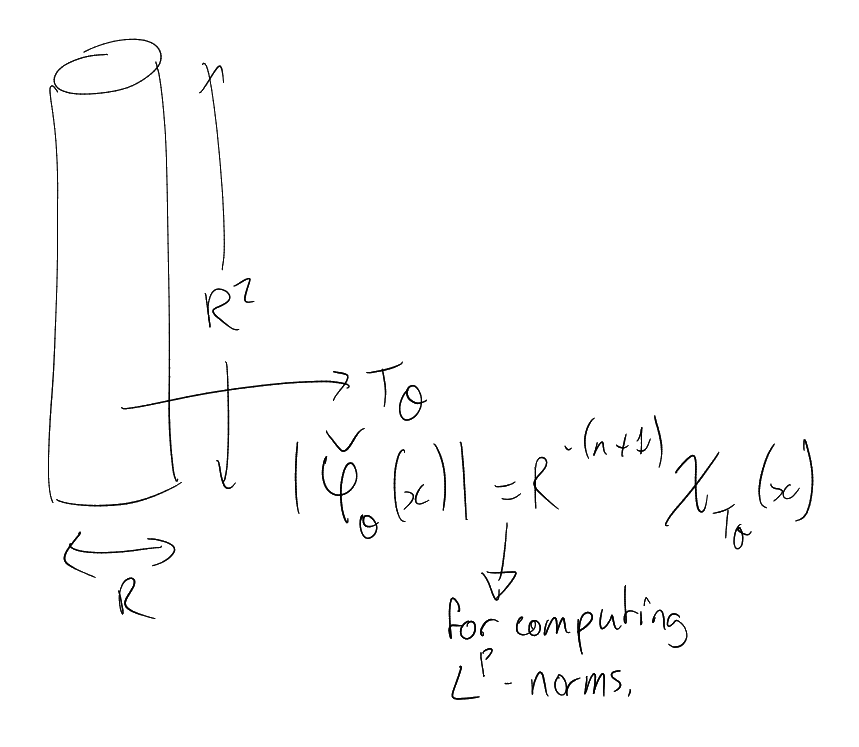Introduction to Fourier Restriction - Fourier Restriction Theory

4 Introduction to Fourier Restriction

Theorem (Hausdorff-Young inequality). Assuming that:

$1 \leq p \leq 2$
$\frac{1}{p} + \frac{1}{q} = 1$

Then

∥ \hat{f} ∥_{q} \leq ∥ f ∥_{p} .

Proof. The inequality is true for $p = 1$ , $q = \infty$ and for $p = 2$ , $q = 2$ the inequality is true since we have equality (Plancherel).

For values in between we can interpolate. □

Are there any other $(p, q)$ for which

∥ \hat{f} ∥_{q} ≲ ∥ f ∥_{p} ? (∗)

We saw that $1 \leq p \leq 2$ was necessary (translations / modulations, Khinchin’s inequality).

Scaling: Plug in $f_{λ} (x) = f (λ x)$ which is $L^{\infty}$ -normalised ( $∥ f_{λ} ∥_{\infty} = ∥ f ∥_{\infty}$ ). Then $\hat{f_{λ}} (ξ) = λ^{- n} \hat{f} (λ^{- 1} ξ)$ which is $L^{1}$ -normalised ( $∥ \hat{f_{λ}} ∥_{1} = ∥ \hat{f} ∥_{1}$ ).

{(LHS of (*))}^{q} = \int_{ℝ^{n}} | \hat{f_{λ}} (ξ) |^{q} d ξ = λ^{- n q + n} \int | \hat{f} (ξ) |^{q} d ξ .

{(RHS of (*))}^{p} = \int_{ℝ^{n}} | f_{λ} (x) |^{p} d x = λ^{- n} \int | f (x) |^{p} d x .

So we need for all $λ > 0$ :

λ^{- n + \frac{n}{q}} ∥ \hat{f} ∥_{q} ≲ λ^{- \frac{n}{p}} ∥ f ∥_{p} .

So we need $- n + \frac{n}{q} = - \frac{n}{p}$ , i.e. $\frac{1}{p} + \frac{1}{q} = 1$ .

Classical questions

What is $C_{p, q}$ the smallest constant such that $∥ \hat{f} ∥_{q} \leq C_{p, q} ∥ f ∥_{p}$ ?

Which functions $f$ satisfy $\frac{∥ \hat{f} ∥_{q}}{∥ f ∥_{p}} = C_{p, q}$ ?

2014:

∥ \hat{f} ∥_{q} \leq C_{p, q} ∥ f ∥_{p} - {dist}_{p} (f, maximisers (Gaussian)) .

Fourier restriction asks which $(p, q)$ permit estimates $∥ \hat{f} ∥_{L^{q} (R)} ≲ ∥ f ∥_{L^{p} (ℝ^{n})}$ ( $R$ is the restricted frequency set, $R \subseteq ℝ^{n}$ ).

Example. $R = B_{1} (0) \subseteq ℝ^{n}$ , unit ball $\to$ : Basically, sitll governed by Hausdorff-Young inequality.

Example. $R = B_{1} (0) \cap {x_{n} = 0}$ (measure $0$ subset of $ℝ^{n}$ ).

$R_{R} (p \to q)$ means

∥ \hat{f} ∥_{L^{q} (R)} ≲ ∥ f ∥_{L^{p} (ℝ^{n})} \forall f : ℝ^{n} \to ℂ Schwartz

Always: $R_{R} (1 \to \infty)$ true for all $R$ .

In the second example, only this trivial statement is true (i.e. $R_{R} (p \to q)$ is false for all other values for $p, q$ ).

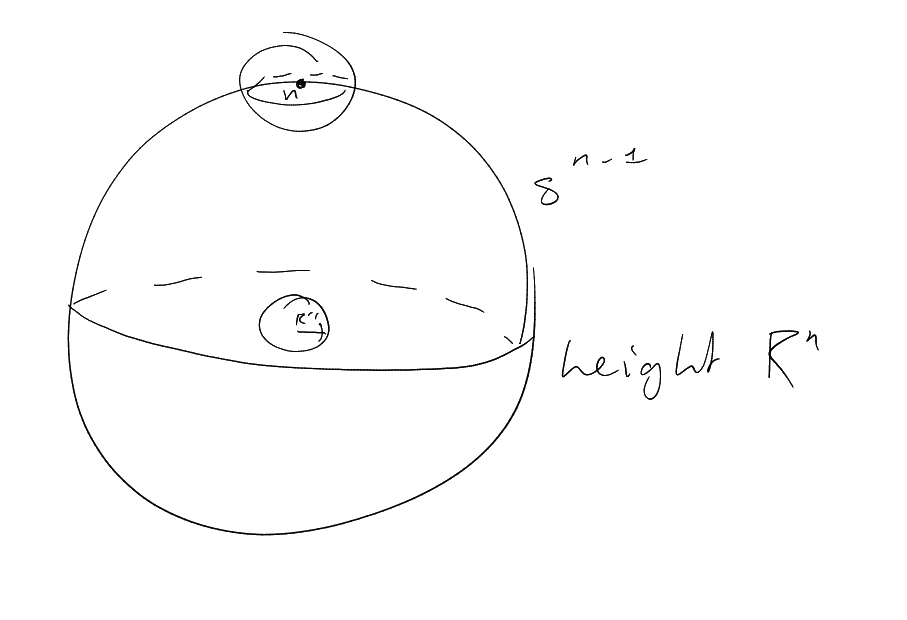
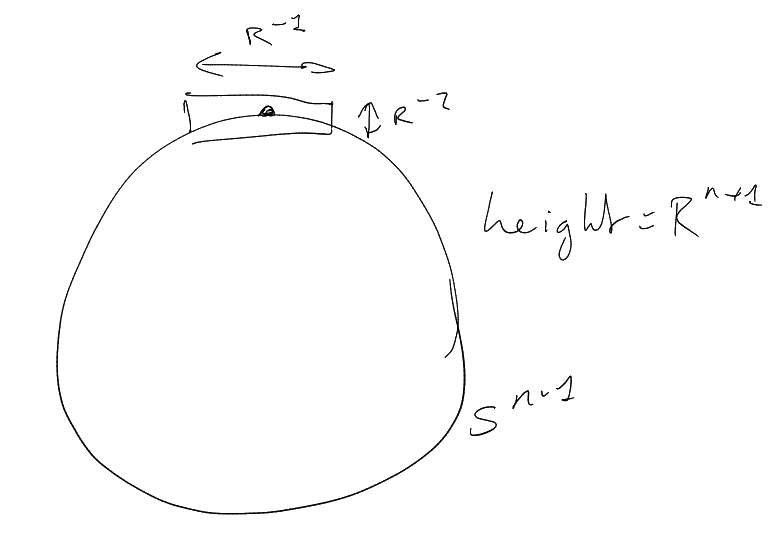
Let $R = S^{n - 1}$ be the unit sphere in $ℝ^{n}$ . Consider

∥ \hat{f} ∥_{L^{q} (S^{n - 1})} ≲ ∥ f ∥_{L^{p} (ℝ^{n})}

where $L^{q} (S^{n - 1})$ uses the usual surface measure $d σ$ on $S^{n - 1}$ .

Notation.

We may call $ˇ$ the “inverse Fourier transform”.

Let $φ \in C_{c}^{\infty} (ℝ^{n})$ , $ℝ$ -valued, $\geq \frac{1}{2}$ on $B_{1} (0)$ , with support in $B_{2} (0)$ .

May also assume $ˇ φ$ is $ℝ$ -valued, $ˇ φ ≳ 1$ on $B_{c} (0)$ . $ˇ φ$ bounded, $| ˇ φ (x) | ≲_{m} {(| x |^{2} + 1)}^{- m} \forall m$ . $| ˇ φ (x) |$ behaves like $χ_{B_{1} (0)}$ in $L^{p}$ .

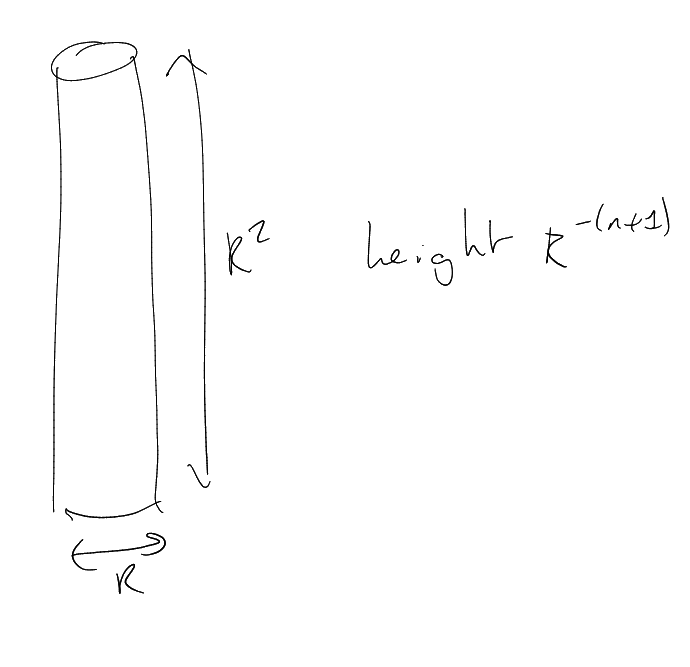
Consider dilates $f_{R} (x) = ˇ φ (R^{- 1} x) e^{2 π i x \cdot v_{r}}$ , $R ≫ 1$ .

Frequency side $| \hat{f_{R}} (ξ) | \sim R^{n} χ_{B_{R^{- 1}} (0)} (x)$ ( $L^{1}$ -norm).

\int_{S^{n - 1}} | \hat{f_{R}} (ξ) |^{q} d σ (ξ) \sim \underset{\to σ (B_{R^{- 1}} (n) \cap S^{n - 1})}{\underset{⏟}{R^{n q} R^{- (n - 1)}}} .

$B_{R^{- 1}} (n) \cap S^{n - 1}$ cap of radius $R^{- 1}$ . Spacial side $| f_{R} (x) | \sim χ_{B_{R} (0)} (x)$ (in $L^{\infty}$ -norm).

height $1$ , $\int_{ℝ^{n}} | f_{R} (x) |^{p} d x \sim R^{n}$ .

$R^{n - \frac{n - 1}{q}} ≲ R^{\frac{n}{p}}$ , $n - \frac{n - 1}{q} \leq \frac{n}{p}$ .

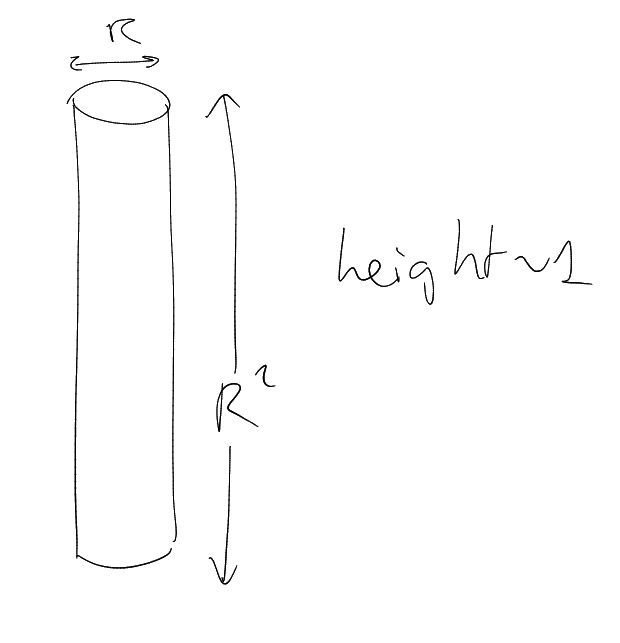
Consider: $g_{R} (x) = e^{i x \cdot w_{r}} ˇ φ (R^{- 1} x_{1}, \dots, R^{- 1} x_{n - 1}, R^{- 2} x_{n})$ .

Frequency: $| \hat{g_{r}} (ξ) | \approx | c y l i n d e r |^{- 1} χ_{c y l i n d e r} (ξ)$ . $| c y l i n d e r |^{- 1} |$ $\to$ ${(R - 1 \cdot R^{- 1} R^{- 2})}^{- 1} = R^{n + 1}$ .

\int_{S^{n - 1}} | \hat{g_{R}} (ξ) |^{q} d σ (ξ) \sim R^{(n + 1) q} σ (cap of radius R^{- 1}) = R^{(n + 1) q - (n - 1)} .

Spatial side: $| g_{R^{'}} (x) | \approx χ_{c y l i n d e r} (x)$ ( $L^{\infty}$ -norm).

$\int | g_{R} (x) |^{p} = R^{n - 1 + 2} = R^{n + 1}$ .

$\to$ $R^{n + 1 - \frac{n - 1}{q}} ≲ R^{\frac{n + 1}{q}}$ , $⟹ n + 1 - \frac{n - 1}{q} \leq \frac{n + 1}{p}$ . Implies B.

On Monday, we will build examples $h$ such that $\hat{h}$ sees all of $S^{n - 1}$ .

$R = S^{n - 1} \subseteq R^{n}$ .

Consider the statement

∥ \hat{f} ∥_{L^{q} (S^{n - 1})} ≲ ∥ f ∥_{L^{p} (ℝ^{n})} .

(recall that we called this $R_{S^{n - 1}} (p \to q)$ ).

Fix $φ \in C_{c}^{\infty} (ℝ^{n})$ , $φ \sim χ_{B_{1} (0)}$ . For computing $L^{p}$ norms, $| \hat{φ} | \sim χ_{B_{c} (0)}$ .

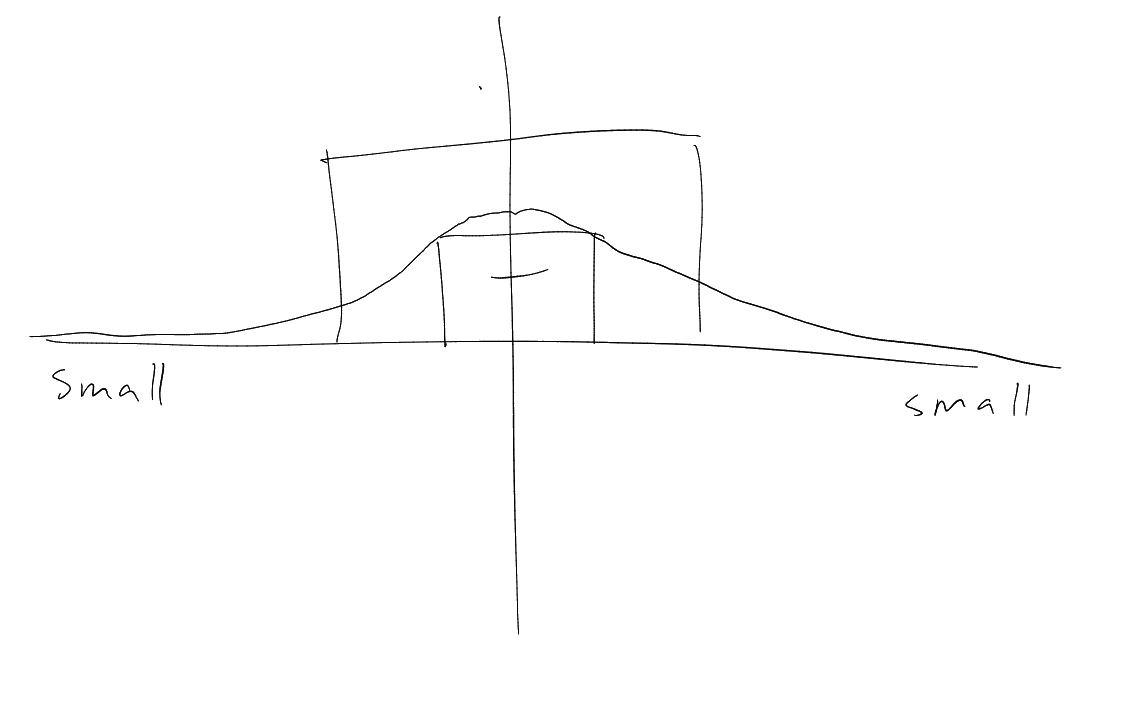
Wave packet function with localised spatial and frequency behaviour.

Last time: $f_{R} (x) = e^{i x \cdot v_{R}} ˇ φ (R^{- 1} x_{1}, \dots, R^{- 1} x_{n - 1}, R^{- 2} x_{n})$ .

Frequency: $| \hat{f_{R}} (ξ) |$

$\int_{S^{n - 1}} | \hat{f_{R}} |^{q} d σ$

n + 1 - \frac{n - 1}{q} \leq \frac{n + 1}{q}

Spatial: $| f_{R} (x) |$

$\int_{ℝ^{1}} | f_{R} |^{p}$

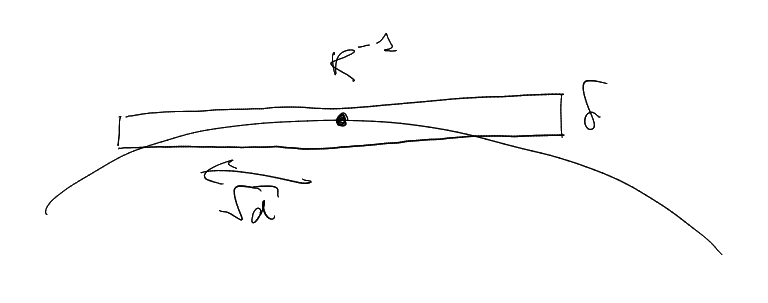
Note: sphere near $n$ looks like $(ξ^{1}, 1 - \frac{1}{2} | ξ^{'} |^{2})$ , $S^{n - 1} \cap supp \hat{f_{R}} \sim cap of radius R^{- 1}$ .

Naive attempt: $g_{R} (x) = R^{n} ˇ φ (R x)$

Frequency: $| \hat{g_{R}} (ξ) |$

$\int_{S^{n - 1}} | \hat{g_{R}} (ξ) |^{q} d ξ \sim 1$

Spatial: $| g_{R} (x) |$

$\int | g_{R} |^{p} \sim R^{- n} \cdot R^{n p}$ .

Deduce: $1 ≲ R^{- \frac{n}{p} + n}$ , so

p \geq 1

(trivial).

$| \hat{g_{R}} | \sim 1$ on $S^{n - 1}$ made $∥ \hat{g_{R}} ∥_{L^{q} (S^{n - 1})}$ easy to compute.

Could we improve things?

Could think about $R \sim 1$ : then $∥ \hat{g_{R}} ∥_{L^{q} (S^{n - 1})} \sim 1$ , $∥ g_{R} ∥_{p} \sim 1$ . This is more efficient, but we can’t take a limit. So not so useful.

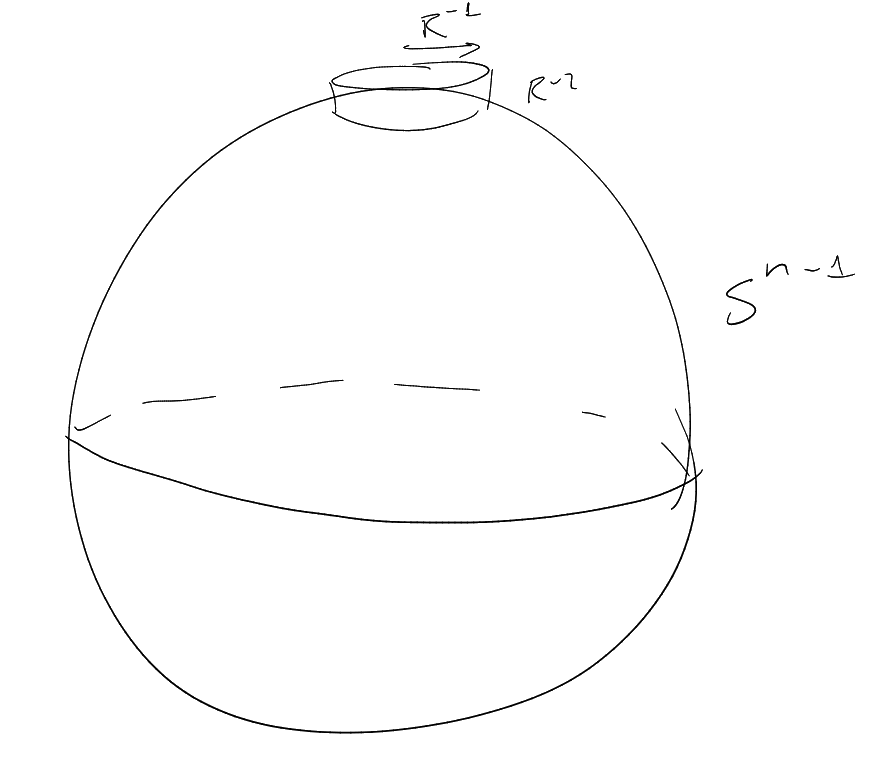
Build a function $H (x)$ which satisfies $| \hat{H} (ξ) | \sim 1$ on $S^{n - 1}$ .

Let ${𝜃}$ be a maximal collection of $\sim R^{- 1}$ -spaced points on $S^{n - 1}$ ( $# {𝜃} \sim R^{n - 1}$ ).

For each $𝜃$ , let $A_{𝜃}^{- 1} : ℝ^{n} \to ℝ^{n}$ be an affine map which sends

B_{1} (0) \to R^{- 1} \times \dots \times R^{- 1} \times R^{- 2} ellipsoid centered at 𝜃, tangent to S^{n - 1} at 𝜃 .

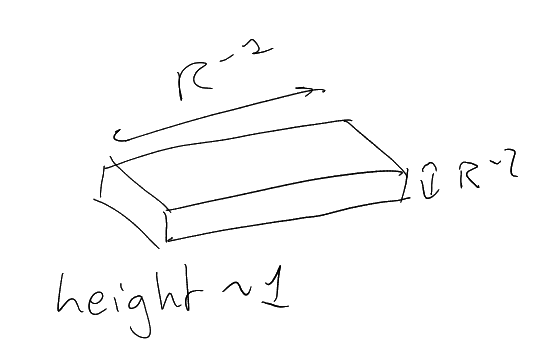
Define $φ_{𝜃} = φ \circ A_{𝜃}$ , $H (x) = \sum_{𝜃} ˇ φ_{𝜃} (x)$ .

$\hat{H} (ξ) = \sum_{𝜃} φ_{𝜃} (ξ) \sim 1$ on $S^{n - 1}$ (actually on $R^{- 2}$ -neighbourhood of $S^{n - 1}$ ).

$\int_{S^{n - 1}} | \hat{H} (ξ) |^{q} d σ \sim 1$ .

$H (x) = \sum_{𝜃} ˇ φ_{𝜃} (x)$ .

$| φ_{𝜃} (x) |$ Frequency:

$| ˇ φ_{𝜃} (x) |$ Spatial:

$ess supp H \supseteq ⋃_{𝜃} ess supp ˇ φ_{𝜃}$ .

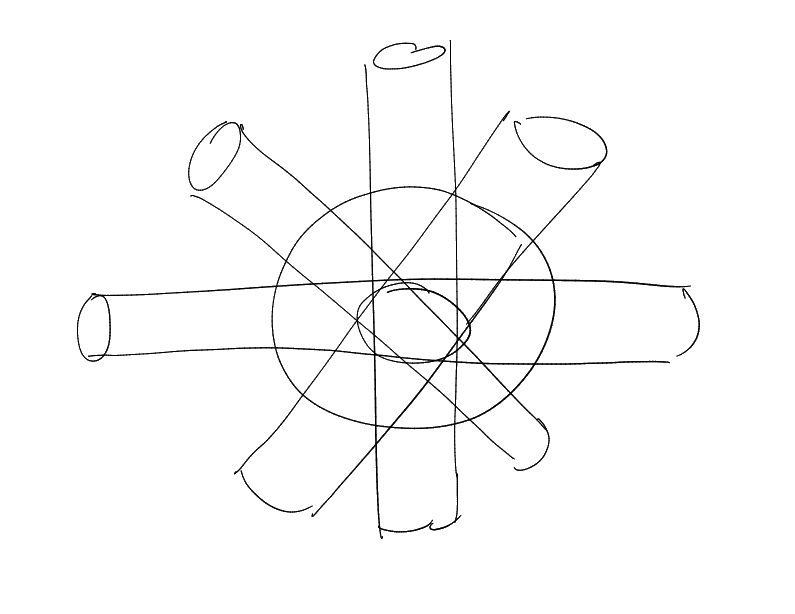
“bush of tubes”

$\sim R^{n - 1}$ many $R \times \dots \times R \times R^{2}$ tubes in $R^{- 1}$ -separated directions

\int_{ℝ^{n}} | H (x) |^{p} d x = \int_{ℝ^{n}} {| \sum_{𝜃} \underset{ℂ -valued function}{\underset{⏟}{ˇ φ_{𝜃} (x)}} |}^{p} d x

Compute

\begin{array}{l} \int_{ℝ^{n}} {| \sum_{𝜃} χ_{T_{𝜃}} {(x)}^{2} |}^{\frac{p}{2}} & = \int_{ℝ^{n}} {| \sum_{𝜃} χ_{T_{𝜃}} (x) |}^{\frac{p}{2}} \\ = \underset{{(R^{n - 1})}^{\frac{p}{2}} \cdot R^{n}}{\underset{⏟}{\int_{B_{R}} {| \sum χ_{T_{𝜃}} |}^{\frac{p}{2}}}} + \underset{(*)}{\underset{⏟}{\int_{R_{R^{2}} ∖ B_{R}} {| \sum χ_{T_{𝜃}} |}^{\frac{p}{2}}}} \end{array}

Consider overlap of $T_{𝜃}$ on $λ S^{n - 1}$ ( $λ \in (R, R^{2})$ ).

Average overlap on $λ S^{n - 1}$ :

- \int_{λ S^{n - 1}} \sum_{𝜃} χ_{T_{𝜃}} \sim λ^{- (n - 1)} \sum_{𝜃} \int_{λ S^{n - 1}} χ_{T_{𝜃}} \sim λ^{- (n - 1)} \sum_{𝜃} R^{n - 1} = λ^{- (n - 1)} R^{2 (n - 1)} .

Not too hard to check that the number of active $T_{𝜃}$ on $λ S^{n - 1}$ is $\sim λ^{- (n - 1)} R^{2 (n - 1)}$ .

Now calculate:

(*) \sim \sum_{R < λ < R^{2}} \int_{λ < | x | < 2 λ} \underset{{[λ^{- (n - 1)} R^{2 (n - 1)}]}^{\frac{p}{2}} λ^{n}}{\underset{⏟}{{| \sum_{𝜃} χ_{T_{𝜃}} |}^{\frac{p}{2}}}} d x .

1 ≲ R^{- (n + 1) p} [R^{2 n} + R^{(n - 1) \frac{p}{2}} R^{n}] .

Two cases: either $R^{2 n}$ dominates or the other term dominates. So $p \leq \frac{2 n}{n + 1}$ .

[next] [prev] [prev-tail] [front] [up]