
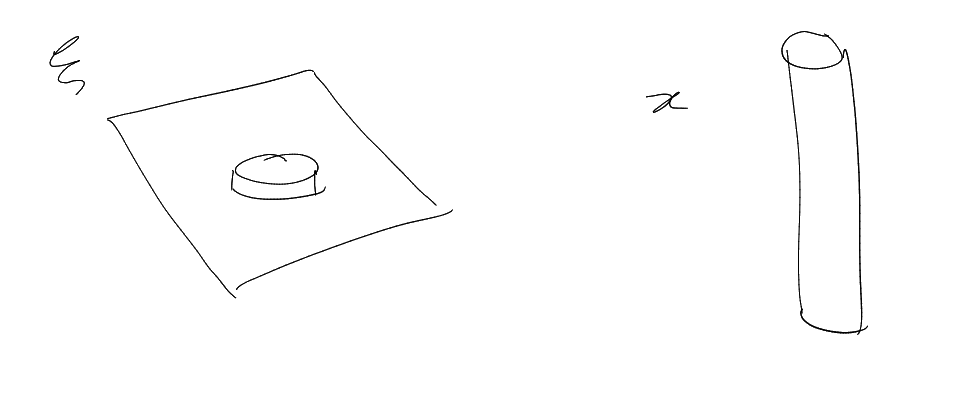

integral equals
“fractal geometry”.
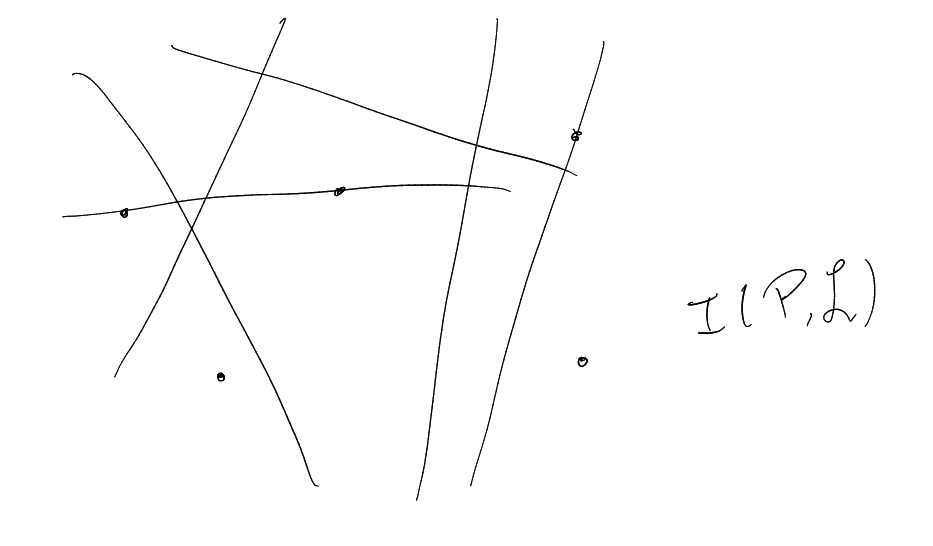
Searching for
|
|




integral equals
“fractal geometry”.

Reminder:
|
|
Conjecture (Restriction Conjecture).
First proved for
Special things happen in
Same conjecture for
|
|
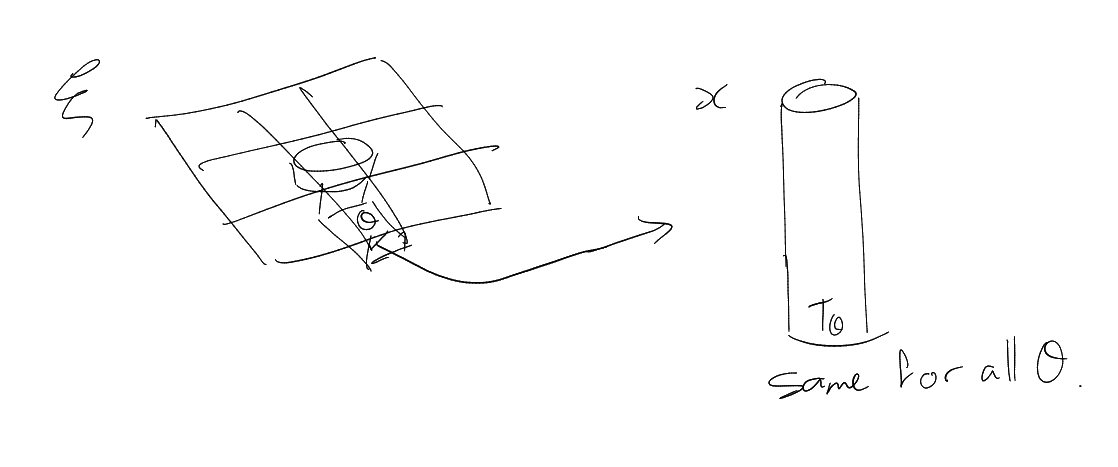
For
Restriction theory can be used to deduce continuum incidence geometry estimates.
Surprisingly, we can go the other way too (very recent progress, whereas the above direction has been well-known since
at least the
Dual version is called “Fourier extension”:
|
|
(
Call the last inequality
Local, dual version: allows us to work with functions, F.T.
For any
|
|
for all
Call this
Let
|
|
Lucy case:
|
|
|
|
Spatial:
|
|
|
|

Frequency

|
|
|
|
|
|
Aiming for
|
|
Lucky case:
|
|
Unlucky case:
|
|
for all
This is equality if
PAUSE THIS.
The locally constant property.
Convolution: Let
|
|
See Young’s convolution:
|
|
when
Example.
|
|
RHS is “average value of
“
Support property:
Convolution and Fourier Transform:
Locally constant property: Let
|
|
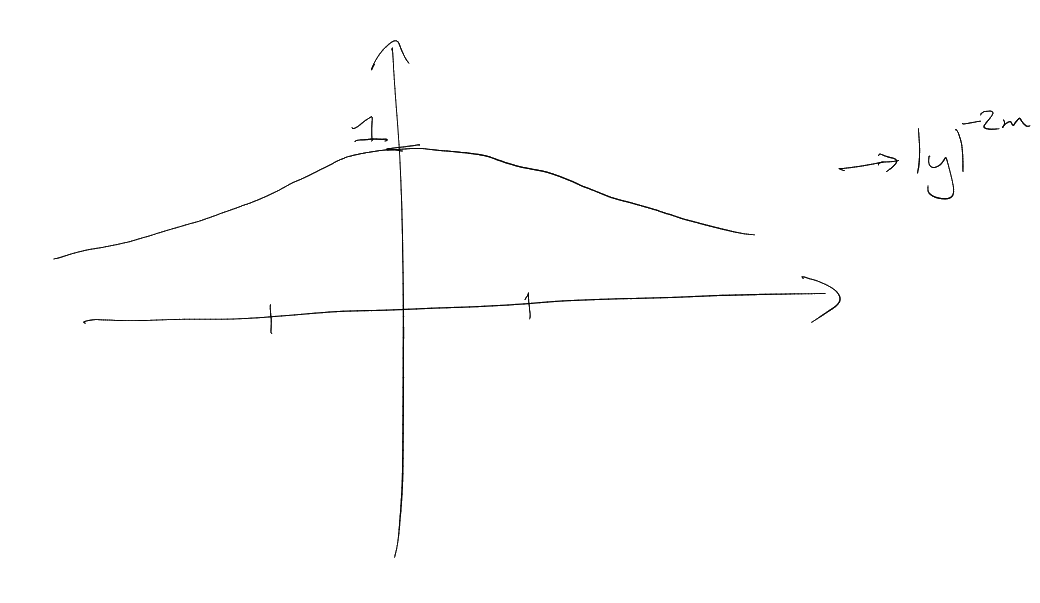
Digesting
For any unit interval
|
|
Suppose this:
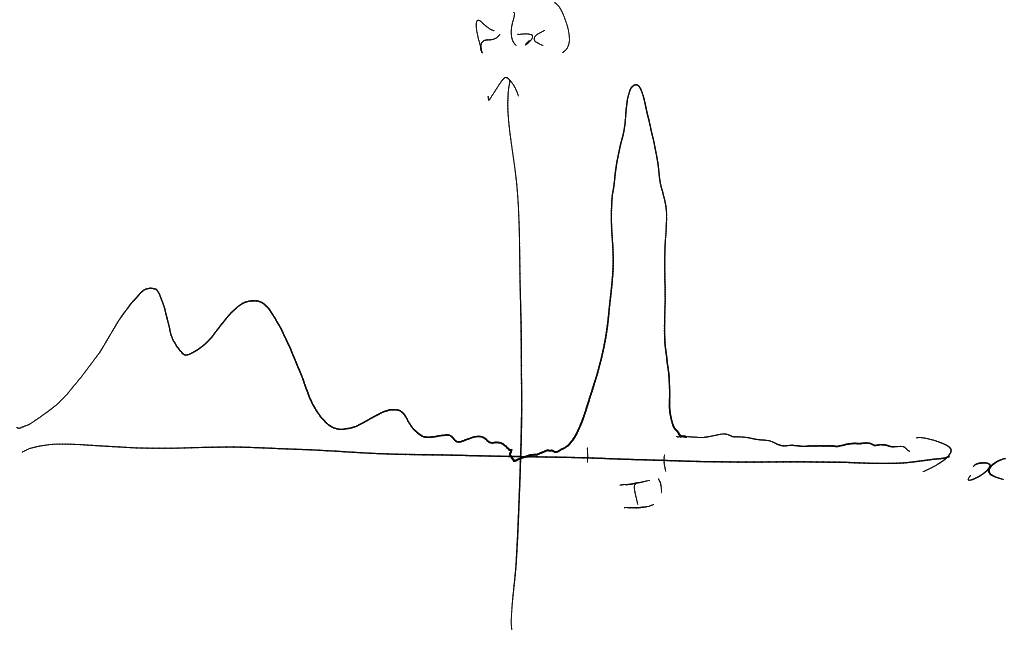
LHS has to be constant.
|
|

|
|
Lemma (Locally constant property). Assuming that:
|
|
The proof of this fact is more important than the statement – we will be using the strategy in future.
Proof of locally constant property.
Let
By Fourier inversion:
|
|
Let
|
|
where
|
|
supported in
Repeat steps of proof:

|
|