Introduction to Fourier Transform - Fourier Restriction Theory

3 Introduction to Fourier Transform

Correction for lecture 2: Number Theory Lemma.

True statements:

\frac{1}{N} \sum_{1 \leq n \leq N} # \div (n) ≲ \log N,

and $# \div (n) ≲_{𝜀} n^{𝜀}$ .

See Terence Tao notes online.

Explaining $# \div (n) ≲_{𝜀} n^{𝜀}$ : $\forall 𝜀 > 0$ , $\exists c_{𝜀} \in (0, \infty)$ such that $# \div (n) \leq C_{𝜀} n^{𝜀}$ for all $n \geq 1$ .

We will be using $≾$ to mean “ $\leq$ but up to sub-polynomial in $n$ ”.

Question:

- \int_{[0, N^{2}]} {| \sum_{n \sim N} b_{n} e (a_{n} x) |}^{p} d x ≾ (1 + N^{\frac{p}{2} - 2}) ∥ b_{n} ∥_{2}^{2} .

For example, $a_{n} = \frac{n^{2}}{N^{2}}$ .

Recall: $n \sim N$ means $N \leq n \leq 2 N$ .

${a_{n}} \subseteq [0, 10]$ , $a_{n + 1} - a_{n} \sim \frac{1}{N}$ , $(a_{n + 2} - a_{n + 1}) - (a_{n + 1} - a_{n}) \sim \frac{1}{N^{2}}$ .

Reasonable conjecture?

Yes, reasonable.

Khinchin’s inequality: May select $b_{n} \in {\pm 1}$ so that

- \int_{[0, N^{2}]} {| \sum_{n} b_{n} e (a_{n} x) |}^{p} d x \sim - \int_{[0, N^{2}]} {| \sum_{n} | b_{n} |^{2} |}^{\frac{p}{2}} d x .

Constant integral: $b_{n} \equiv 1$ . $(1, 1, 1, \dots, 1)$ .

- \int_{[0, N^{2}]} {| \sum_{n} e (a_{n} x) |}^{p} d x ≳ \frac{1}{N^{2}} \int_{[0, c]} N^{p} d x \sim N^{p - 2} = N^{\frac{p}{2} - 2} ∥ b_{n} ∥_{2}^{p} .

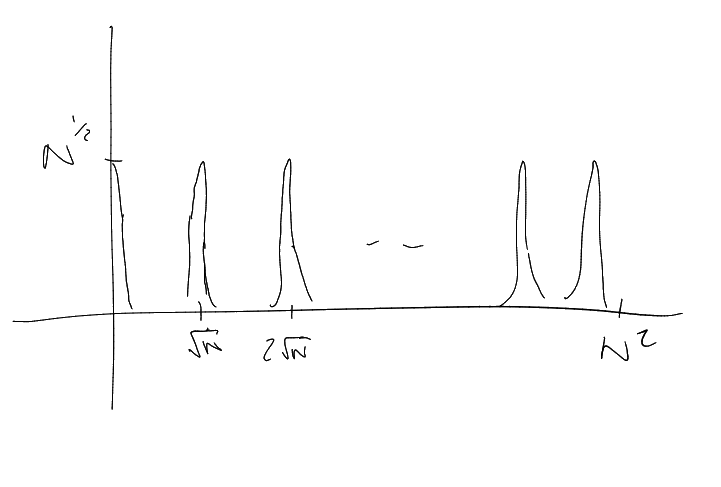
Warning. Enemy scenario: ${a_{n}} = {\sqrt{\frac{n}{N}}}_{n = N}^{2 N}$ (technically ${- \sqrt{\frac{3 N - n}{N}}}$ if we want to satisfy the conditions mentioned above).

$(b_{n}) = (1, 0, \dots, 0, 1, 0, \dots, 0, 1, \dots, 0)$ . Length $N$ vector with $N^{\frac{1}{2}}$ many $1$ s. Have:

- \int_{[0, N^{2}]} {| \sum_{N \leq m^{2} \leq 2 N} e (\sqrt{\frac{m^{2}}{N}} x) |}^{p} d x = - \int_{[0, N^{2}]} {| \sum_{m^{2} \sim N} e (\frac{m}{\sqrt{N}} x) |}^{p} d x

We can calculate that the above expression is in fact $\geq N^{\frac{p}{2} - \frac{1}{2}}$ (which breaks the conjecture until $p > 6$ ).

It turns out that this is (roughly speaking) the only problem.

Why do we care?

$b_{n} \equiv 1$ , $p = 4$ . Then

- \int_{[0, N^{2}]} {| \sum_{n} e (a_{n} x) |}^{4} d x ≾ N^{2} = | {a_{n}} |^{2} .

⟹ # {a_{n_{1}} + a_{n_{2}} = a_{n_{3}} + a_{n_{4}}} ≲ | {a_{n}} |^{2} .

$\to$ Convex sequences have minimal additive energy.

Decoupling doesn’t know how to take advantage of $b_{n} \equiv 1$ .

3.1 Fourier Transform on $ℝ^{n}$

$f : ℝ^{n} \to ℂ$ , $f \in S (ℝ^{n})$ Schwartz function: $∥ x^{α} \partial^{β} f ∥_{\infty} < \infty$ for all $α, β$ .

\hat{f} (ξ) = \int_{ℝ^{n}} e^{- 2 π i x \cdot ξ} f (x) d x .

$x$ is the spatial variable, and $ξ$ is the frequency variable.

Facts:

If $f \in S$ , then $\hat{f} \in S$ .
Plancherel’s Theorem: $\int f (x) \bar{g (x)} d x = \int \hat{f} (ξ) \bar{ĝ (ξ)} d ξ$ .
$f (x) = e^{- π x^{2}}$ , $\hat{f} (ξ) = e^{- π ξ^{2}}$
$λ > 1$

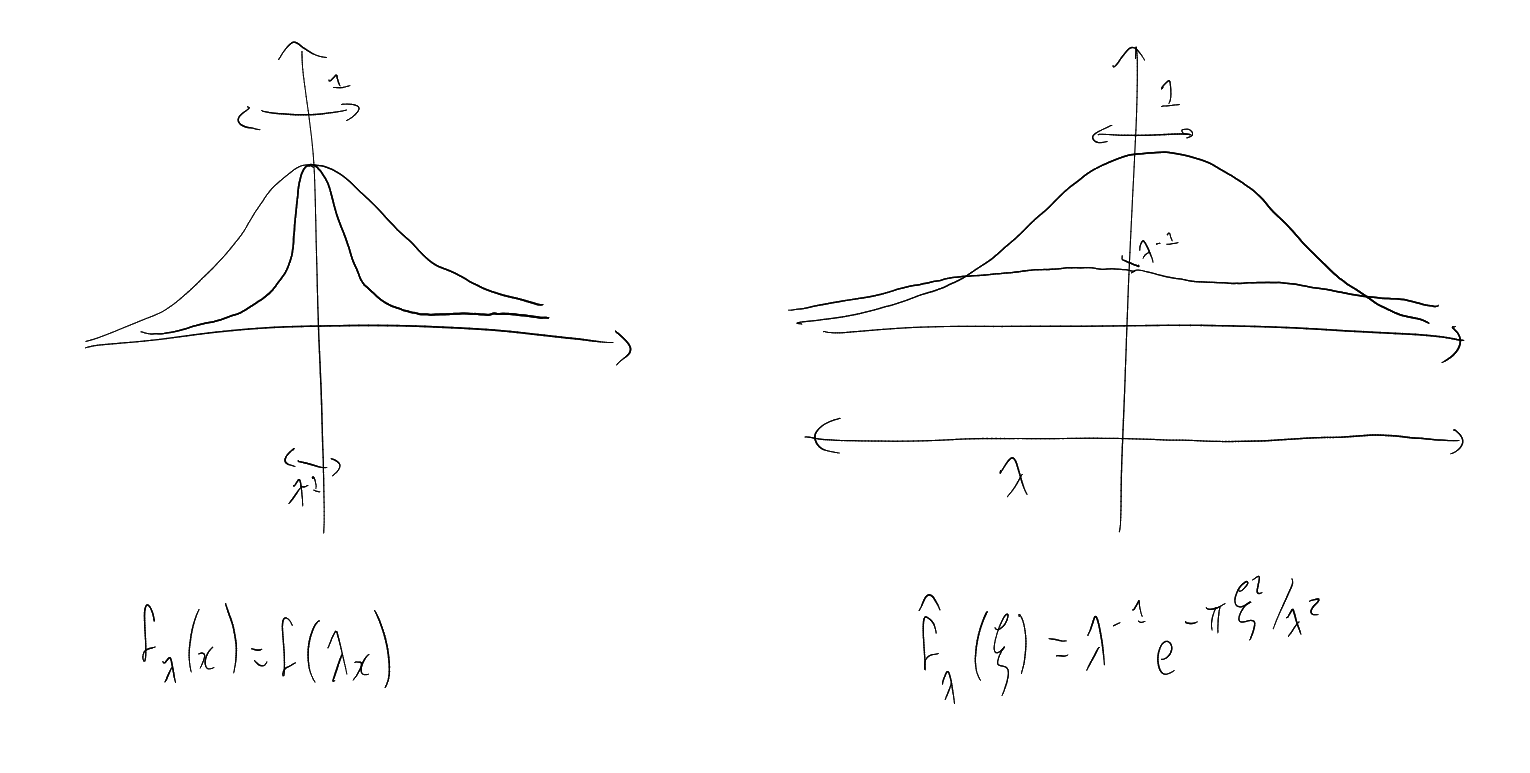
On the left: mass of $f$ is smashed by a factor of $λ$ . On the right: the mass of $\hat{f}$ is stretched by a factor of $λ$ , “ $L^{1}$ normalized”. $∥ \hat{f_{λ}} ∥_{1}$ is independent of $λ$ .

There is a general formula for $\hat{f \circ A}$ where $A$ is an affine transformation.
$\hat{c f + g} = c \hat{f} + \hat{g}$ .
Translations are dual to modulations:
$\begin{array}{l} f_{τ} (x) & = f (x - τ) \\ \hat{f_{τ}} (ξ) & = e^{- 2 π i ξ \cdot τ} \hat{f} (ξ) \\ f^{t} a u (x) & = e^{2 π i τ \cdot x} f (x) \\ \hat{f^{τ}} (ξ) & = \hat{f} (ξ - τ) \end{array}$

Basic question about $\hat{f}$ : $L^{p}$ to $L^{q}$ boundedness?

Plancherel’s:

∥ \hat{f} ∥_{2}^{2} = \int \hat{f} \bar{\hat{f}} = \int f \bar{f} = ∥ f ∥_{2}^{2}

(isometry on $L^{2}$ ).

$p = 1$ , $q = \infty$ :

| \int e^{- 2 π i x \cdot ξ} f (x) d x | \leq \int | f (x) | d x = ∥ f ∥_{1}

(contraction from $L^{1}$ to $L^{\infty}$ ).

By interpolation (Marcinkiewicz): $∥ \hat{f} ∥_{q} \leq ∥ f ∥_{p}$ for $1 \leq p \leq 2$ , $\frac{1}{p} + \frac{1}{q} = 1$ (Hausdorff-Young inequality).

Are there any other $(p, q)$ for which

∥ \hat{f} ∥_{q} ≲_{p, q} ∥ f ∥_{q} ?

Attempt 1: Let $φ \in C_{c}^{\infty} (ℝ^{n})$ (compactly supported smooth function on $ℝ^{n}$ ), with $supp φ \subseteq B_{1} (0)$ .

Consider $f (x) = \sum_{k = 1}^{N} 𝜀_{k} φ (x - v_{k})$ .

Choose $v_{k}$ so that ${B_{1} (v_{k})}$ are not overlapping. Then

∥ f ∥_{p}^{p} = \int {| \sum_{k} 𝜀_{k} φ (x - v_{k}) |}^{p} = \sum_{k} \int | φ (x - v_{k}) |^{p} d x = N ∥ φ ∥_{p}^{p} .

Also

\hat{f} (ξ) = \sum_{k = 1}^{N} 𝜀_{k} e^{- 2 π i ξ v_{k}} \hat{φ} (ξ) = (\sum_{k = 1}^{N} 𝜀_{k} e^{- 2 π i ξ v_{k}}) \hat{φ} (ξ) .

We will use Khinchin’s inequality.

$∥ \hat{f} ∥_{q} \sim N^{\frac{1}{2}} ∥ \hat{φ} ∥_{q}$ .

[next] [prev] [prev-tail] [front] [up]

3 Introduction to Fourier Transform

3.1 Fourier Transform on ℝn

3.1 Fourier Transform on $ℝ^{n}$