The Group Law - Elliptic Curves - Cambridge III notes

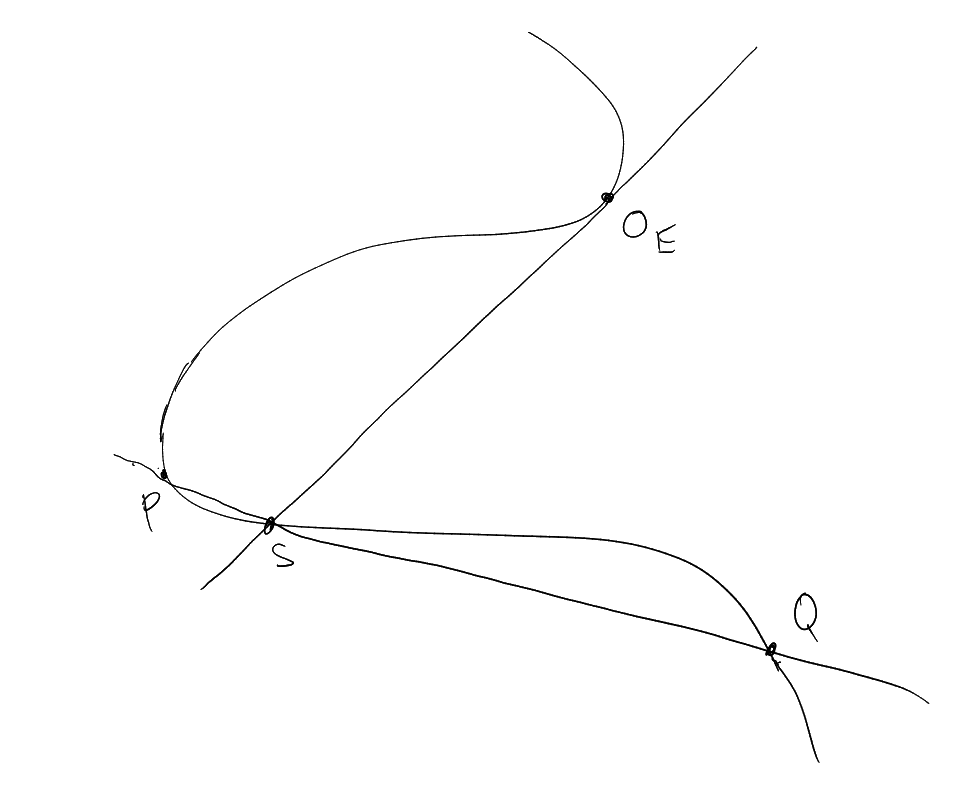
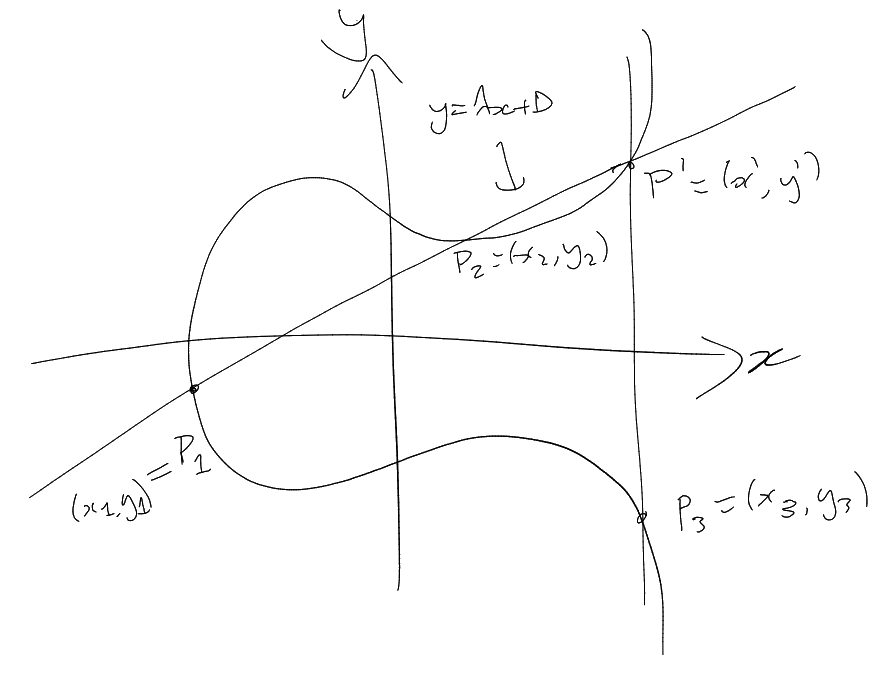
4 The Group Law

Let $E \subset ℙ^{2}$ be a smooth plane cubic, and $0_{E} \in E (K)$ .

$E$ meets any line in 3 points counted with multiplicity.

Let $S$ be the third point of intersection of $P Q$ with $E$ , and $R$ be the third intersection point of $0_{E} S$ and $E$ .

Define $P \oplus Q = R$ .

If $P Q$ then take $T_{P} E$ instead of $P Q$ etc.

This is called the “chord and tangent process”.

Theorem 4.1. $(E, \oplus)$ is an abelian group.

Note. $E$ here means $E (\bar{K})$ . As mentioned before, we only ever mean “over $K$ ” if it is explicitly mentioned (otherwise we are always working “over $\bar{K}$ ”).

Proof.

(i) $\oplus$ is clearly commutative.
(ii) $0_{E}$ is the identity:

$0_{E} \oplus P = P$ .
(iii) Inverses:

Let $S$ be the third point of intersection of $T_{0_{E}} E$ and $E$ , and let $Q$ be the third point of intersection of $P S$ and $E$ .

Then $P \oplus Q = 0_{E}$ .
(iv) Associativity: much harder! We will develop a bit of theory first. □

Definition (Linearly equivalent). $D_{1}, D_{2} \in Div (E)$ are linearly equivalent if there exists $f \in \bar{K} {(E)}^{*}$ such that $div (f) = D_{1} - D_{2}$ .

Write $D_{1} \sim D_{2}$ and $[D] = {D^{'} : D^{'} \sim D}$ .

Definition. $Pic (E) = \frac{Div (E)}{\sim}$ , ${Pic}^{0} (E) = \frac{{Div}^{0} (E)}{\sim}$ . where ${Div}^{0} (E) = {D \in Div E | \deg D = 0}$ .

Proposition 4.2. Assuming that:

we define
$\begin{array}{l} ψ : E & \to {Pic}^{0} (E) \\ P & \mapsto [(P) - (0_{E})] \end{array}$

Then

(i) $ψ (P \oplus Q) = ψ (P) + ψ (Q)$ .
(ii) $ψ$ is a bijection.

Proof.

(i) $\begin{array}{l} div (l ∕ m) & = (P) + (S) + (Q) - (0_{E}) - S - (R) \\ = (P) + (Q) - (0_{E}) - (P \oplus Q) \end{array}$
Hence $(P) + (Q) \sim (P \oplus Q) + (0_{E})$ . Therefore $(P \oplus Q) - (0_{E}) \sim (P) - (0_{E}) + (Q) - (0_{E})$ . So $ψ (P \oplus Q) = ψ (P) + ψ (Q)$ .
(ii) Injectivity: Suppose $ψ (P) = ψ (Q)$ with $P \neq Q$ .
Then there exists $f \in \bar{K} {(E)}^{*}$ such that $div (f) = (P) - (Q)$ , so $E \overset{f}{\to} ℙ^{1}$ has degree 1, hence $E ≅ ℙ^{1}$ , contradiction.

Note: We now compute
$ψ ((P \oplus Q) \oplus R) = ψ (P) + ψ (Q) + ψ (R) = ψ (P \oplus (Q \oplus R))$

hence $(P \oplus Q) \oplus R = P \oplus (Q \oplus R)$ for all $P, Q, R \in E$ (using injectivity). So $(E, \oplus)$ is associative.

(iii) Surjectivity: Let

[D] \in {Pic}^{0} (E)

. Then

D + (0_{E})

has degree

1

Riemann Roch gives $\dim L (D + (0_{E})) = 1$ . So there exists $0 \neq f \in \bar{K} (E)$ such that

\underset{degree 1}{\underset{⏟}{div (f) + D + (0_{E})}} \geq 0 .

div (f) + D + (0_{E}) = (P)

for some $P \in E$ . Then $(P) - (0_{E}) \sim D$ , so $ψ (P) = [D]$ . □

Formulae for $E$ in Weierstrass form

E : y^{2} + a_{1} x y + a_{3} y = x^{3} + a_{2} x^{2} + a_{4} x + a_{6} (∗)

$0_{E} = (0 : 1 : 0)$ .

$P_{1} \oplus P_{2} = P_{3}$ . $⊖ P_{1} = (x_{1}, - (a_{1} x + a_{3}) - y_{1})$ .

Substituting $y = λ x + ν$ into ( $*$ ) and looking at coefficient of $x^{2}$ gives

λ^{2} + a_{1} λ - a_{2} = x_{1} + x_{2} + \underset{= x_{3}}{\underset{⏟}{x^{'}}} .

Therefore

\begin{array}{l} x_{3} & = λ^{2} + a_{1} λ - a_{2} - x_{1} - x_{2} \\ y_{3} & = - (a_{1} x^{'} + a_{3}) - y^{'} \\ = - (a_{1} x_{3} + a_{3}) - (λ x_{3} + ν) \\ = - (λ + a_{1}) x_{3} - a_{3} - ν \end{array}

It remains to find formulae for $λ$ and $ν$ .

Case I $x_{1} = x_{2}$ , $P_{1} \neq P_{2}$ . Then $P_{1} \oplus P_{2} = 0_{E}$ .
Case II $x_{1} \neq x_{2}$ . $\begin{array}{l} λ & = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ ν & = y_{1} + λ x_{1} \\ = \frac{y_{1} (x_{2} - x_{1}) - x_{1} (y_{2} - y_{1})}{x_{2} - x_{1}} \\ = \frac{x_{2} y_{1} - x_{1} y_{2}}{x_{2} - x_{1}} \end{array}$
Case III $P_{1} = P_{2}$ . $\begin{array}{l} λ & = \dots \\ ν & = \dots \end{array}$
(Compute equation for tangent line.)

Corollary 4.3. $E (K)$ is an abelian group.

Proof. It is a subgroup of $(E, \oplus)$ . Identity $0_{E} \in E (K)$ by definition.

Closure / inverses: see formulae above.

Associative / commutative: inherited. □

Theorem 4.4. Elliptic curves are group varieties, i.e. $[- 1] : E \to E$ ; $P \mapsto ⊖ P$ and $\oplus : E \times E \to E$ ; $(P, Q) \mapsto P \oplus Q$ are morphisms of algebraic varieties.

Proof.

(i) Above formulae imply $[- 1] : E \to E$ is a rational map, and hence a morphism (by Remark 2.9).

(ii) Above formulae imply

\oplus : E \times E \to E

is a rational map regular on

U = {(P, Q) \in E \times E | P, Q, P \oplus Q, P ⊖ Q \neq 0_{E}} .

For $P \in E$ , let $τ_{P} : E \to E$ ; $X \mapsto X \oplus P$ “translation by $P$ ”.

$τ_{P}$ is a rational map, and hence a morphism (by Remark 2.9).

Take any $A, B \in E$ . We factor $\oplus$ as

E \times E \overset{τ_{⊖ A} \times τ_{⊖ B}}{\to} E \times E \overset{\oplus}{\to} E \overset{τ_{A \oplus B}}{\to} E .

This shows $\oplus$ is regular on $(τ_{A} \times τ_{B}) (U)$ for all $A, B \in E$ . Therefore $\oplus$ is regular on $E \times E$ . □

Statement of Results

The isomorphisms in (i), (ii), (iv) respect the relevant topologies.

(i) $K = ℂ$ , $E (ℂ) = ℂ ∕ Λ ≅ ℝ ∕ ℤ \times ℝ ∕ ℤ$ ( $Λ$ is a lattice).
(ii) $K = ℝ$ . Then
$E (ℝ) = {\begin{matrix} ℤ ∕ 2 ℤ \times ℝ ∕ ℤ & if Δ > 0 \\ ℝ ∕ ℤ & if Δ < 0 \end{matrix}$
(iii) $K = 𝔽_{q}$ (field with $q$ elements). Then
$| # E (𝔽_{q}) - (q + 1) | \leq 2 \sqrt{q} .$

(Hasse’s Theorem).
(iv) $[K : ℚ_{p}] < \infty$ , ring of integers $O_{K}$ . $E (K)$ has a subgroup of finite index which is isomorphic to $(O_{K}, +)$ .
(v) $[K : ℚ] < \infty$ . $E (K)$ is a finitely generated abelian group (Mordell-Weil Theorem).

Brief remarks on the case $K = ℂ$

Let

Λ = {a ω_{1} + b ω_{2} : a, b \in ℤ},

where $ω_{1}, ω_{2}$ a basis for $ℂ$ as an $ℝ$ -vector space.

Then

{meromorphic functions on the Riemann surface ℂ ∕ Λ} \leftrightarrow {Λ -invariant meromorphic functions on ℂ} .

The function field of $ℂ ∕ Λ$ is generated by

\begin{array}{l} ℘ (z) & = \frac{1}{z^{2}} + \sum_{0 \neq λ \in Λ} (\frac{1}{{(z - λ)}^{2}} - \frac{1}{λ^{2}}) \\ ℘^{'} (z) & = - 2 \sum_{λ \in Λ} \frac{1}{{(z - λ)}^{3}} \end{array}

These satisfy

℘^{'} {(z)}^{2} = 4 ℘ {(z)}^{3} - g_{2} ℘ (z) - g_{3}

for some $g_{2}, g_{3} \in ℂ$ depending only on $Λ$ .

One shows $ℂ ∕ Λ = E (ℂ)$ (isomorphism as groups and as Riemann surfaces) where $E$ : $y^{2} = 4 x^{3} - g_{2} x - g_{3}$ .

Theorem (Uniformisation Theorem). Every elliptic curve over $ℂ$ arises this way (one proof uses modular forms).

Definition. For $n \in ℤ$ , let $[n] : E \to E$ be defined by

P \mapsto \underset{n copies}{\underset{⏟}{P \oplus P \oplus \dots \oplus P}}

for $n \geq 0$ , and $[- n] = [- 1] \circ [n]$ .

Definition ( $n$ -torsion subgroup). The $n$ -torsion subgroup of $E$ is

E [n] = \ker (E \overset{[n]}{\to} E) .

If $K = ℂ$ then $E (ℂ) ≅ ℂ ∕ Λ$ . Therefore

{\begin{matrix} E [n] ≅ {(ℤ ∕ n ℤ)}^{2} & (1) \\ \deg [n] = n^{2} & (2) \end{matrix}

We’ll show (2) holds over any field $K$ , and (1) holds if $char K ∤ n$ .

Lemma 4.5. Assuming that:

$char K \neq 2$
$E$ : $y^{2} = f (x) = (x - e_{1}) (x - e_{2}) (x - e_{3})$ , $e_{1}, e_{2}, e_{3} \in \bar{K}$

Then

E [2] = {0_{E}, (e_{1}, 0), (e_{2}, 0), (e_{3}, 0)} ≅ {(ℤ ∕ 2 ℤ)}^{2}

Proof. Let $P = (x, y) \in E$ . Then

\begin{array}{l} [2] P = 0 & ⟹ P = - P \\ ⟹ (x, y) = (x, - y) \\ ⟹ y = 0 □ \end{array}

[next] [prev] [prev-tail] [front] [up]

4 The Group Law

Formulae for E in Weierstrass form

Statement of Results

Brief remarks on the case K=ℂ

Formulae for $E$ in Weierstrass form

Brief remarks on the case $K = ℂ$