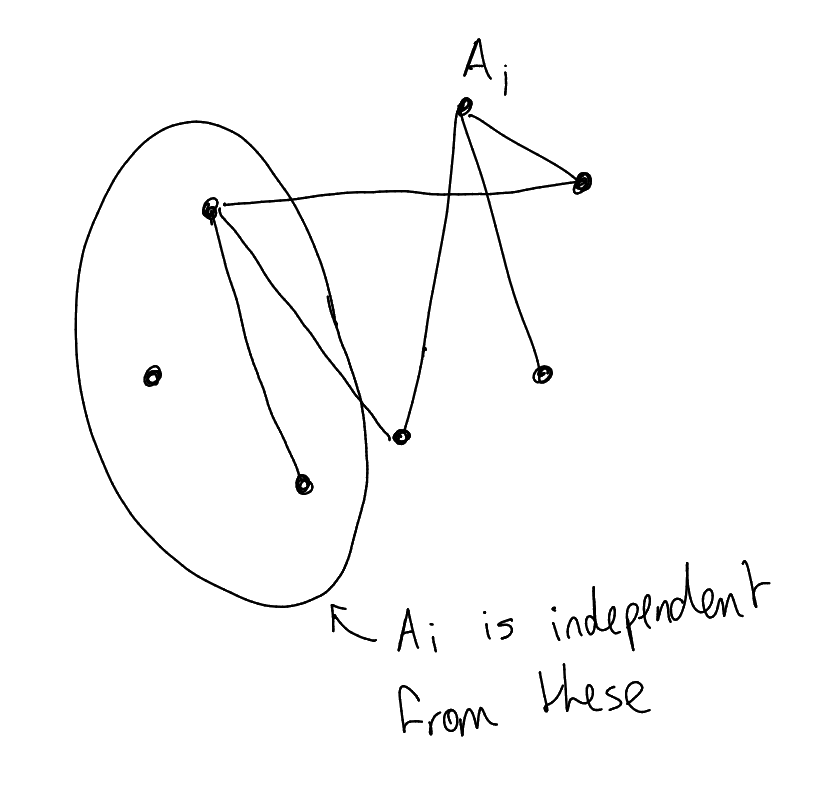Lovasz-Erdős Local Lemma - Probabilistic Combinatorics

4 Lovasz-Erdős Local Lemma

What is the idea fo a local lemma? It’s a general statement in probability about when a certain probability is non-zero.

A silly example: Say I have $100$ independent coins. How do I prove that there exists a configuration of these coins such that everything is heads?

Our earlier techniques don’t work on something like this: before we either started with an event that holds with probability, or something that is close to an event that holds with high probability. $100$ heads is neither of these things, but obviously it exists because everything is independent.

The Local Lemma allows us to show that the probability of an event is non-zero provided we have “enough” independence, which we make precise below.

Lemma 4.1 (Erdős-Lovasz, 70s). Assuming that:

$F = {A_{i}}$ is a family of events in a probability space
$G$ a dependency graph of $F$
$ℙ (A_{i}) \leq \frac{1}{e (Δ + 1)}$ , where $Δ = Δ (G)$ is the max degree of $G$

Then

ℙ (⋂_{i} A_{i}^{c}) > 0 .

Definition 4.2 (Dependency graph). If $F = {A_{i}}$ is a family of events, a dependency graph $G$ is a graph with vertex set $F$ , with the property that: for all $i$ , the event $A_{i}$ is independent from ${A_{j} : A_{j} ⁄ \sim A_{i}}$ .

Note that a family of events $F$ can have many possible dependency graphs, but in applications there is often a particularly natural choice to take.

Picture:

Reminder: $A_{i}$ is independent from ${A_{j} : A_{j} ⁄ \sim A_{i}}$ if $E$ is formed by taking intersections of $A_{j}, A_{j}^{c} ⁄ \sim A_{i}$ , we have

ℙ (A_{i} \cap E) = ℙ (A_{i}) ℙ (E) .

Theorem 4.3 (Spencer). $R (k) \geq (1 + o (1)) \frac{\sqrt{2} k}{e} 2^{k ∕ 2}$ .

Proof. Let $δ > 0$ and let $n = (1 - δ) \frac{\sqrt{2} k}{e} 2^{k ∕ 2}$ . Choose a colouring uniformly at random. For every $S \in {[n]}^{(k)}$ , define the event

A_{S} = “ S^{(2)} are monochromatic” .

We clearly have $ℙ (A_{S}) = 2^{- (\binom{k}{2}) + 1}$ .

Let $G$ be a dependency graph on ${A_{S}}_{S}$ , where we say $A_{S} \sim A_{T}$ if $S^{(2)} \cap T^{(2)} \neq \emptyset$ .

Δ = Δ (G) \leq (\binom{k}{2}) \cdot (\binom{n - 2}{k - 2}) \leq k^{4} \cdot (\frac{1}{n^{2}}) (\binom{n}{k})

We now check:

Δ \cdot 2^{- (\binom{k}{2}) + 1} \leq 2 k^{4} (\frac{1}{n^{2}}) {(\frac{e n}{k})}^{k} 2^{- (\binom{k}{2})} = {[(1 + o (1)) \frac{1}{n^{2 ∕ k}} (\frac{e n \sqrt{2}}{k} \cdot 2^{- k ∕ 2})]}^{k} .

This $\to 0$ . So the condition in Local Lemma holds for sufficiently large $k$ . □

Remark. This is the best known lower bound for diagonal Ramsey.

Definition 4.4 ( $k$ -uniform hypergraph). Say $H$ is a $k$ -uniform hypergraph on vertex set $X$ if $H \subset X^{(k)}$ .

Definition 4.5 (Colourable hypergraph). Say a hypergraph $H$ is $2$ -colourable if there exists $χ : X \to {red, blue}$ such that there is no monochromatic $e \in H$ .

Theorem 4.6. Assuming that:

$H$ a $k$ -uniform hypergraph with maximum degree $d$
$d \leq \frac{2^{k - 1}}{e k} - 1$

Then

H

2

-colourable.

Note. This theorem has no condition on $| H |$ in the assumptions. Thus, this theorem is not just picking out a high probability event out of all uniformly random colourings: if $| H |$ is large and has a reasonable number of edges, then with high probability there will be a monochromatic edge.

Proof. We choose our colouring of the ground set $X$ uniformly at random. For each $e \in H$ , define the event

A_{e} = “ e monochromatic” .

We have $ℙ (A_{e}) = 2^{- k + 1}$ , so we want $2^{- k + 1} \leq \frac{1}{e (Δ + 1)}$ . Note if we define our dependency graph $G$ by $A_{e} \sim A_{f}$ if $e \cap f \neq \emptyset$ , then

Δ (G) \leq d \cdot k .

Now just use the bound on $d$ in the hypothesis. □

Remark. Actually, our second application implies the first on $R (k)$ : just let $H$ be the $(\binom{k}{2})$ -uniform hypergraph on $X = {[n]}^{(2)}$ , defined by

H = {S^{(2)} : S \in {[n]}^{(k)}} .

We now move onto proving Local Lemma.

Theorem 4.7 (Lopsided Local Lemma). Assuming that:

$F = {A_{i}}$ a family of events
$G$ a dependency graph
$x_{1}, \dots, x_{n} \in (0, 1)$ be such that $\forall i$ ,

$ℙ (A_{i}) \leq x_{i} \prod_{A_{i} \sim A_{j}} (1 - x_{j})$

(where $A_{i} \sim A_{j}$ denotes adjacency in the dependency graph).

Then

ℙ (⋂_{i = 1}^{n} A_{i}^{c}) \geq \prod_{i = 1}^{n} (1 - x_{i}) .

This is slightly more mysterious than the first form, but it can be much more useful. Specifically, if the probabilities $ℙ (A_{i})$ aren’t all the same, then this lopsided form allows us to tune the values of $x_{i}$ more precisely than if we just use Local Lemma. We’ll see an example of this at the end of this section.

Proof. We use

ℙ (A \cap B) = ℙ (A | B) ℙ (B) .

Applying this many times, we have

\begin{array}{l} ℙ (⋂_{i = 1}^{n} A_{i}^{c}) & = \prod_{i = 1}^{n} ℙ (A_{i}^{c} | A_{1}^{c} \cap \dots \cap A_{i - 1}^{c}) \\ = \prod_{i = 1}^{n} (1 - \underset{\leq x_{i} ?}{\underset{⏟}{ℙ (A_{i} | A_{1}^{c} \cap \dots \cap A_{i - 1}^{c})}}) \end{array}

We will prove that this term is $\leq x_{i}$ by instead proving the more general statement:

(*) = ℙ (A_{i} | ⋂_{j \in S} A_{j}^{c}) \leq x_{i},

where $S \subset [n] ∖ {i}$ . We prove by induction on $| S |$ .

If $S = \emptyset$ , then done by hypothesis.

If $S \neq \emptyset$ , then define

D = ⋂_{\begin{array}{c} j \in S \\ j \sim i \end{array}} A_{j}^{c}, I = ⋂_{j \in S j ⁄ \sim i} A_{j}^{c} .

Note that

\begin{array}{l} (*) & = ℙ (A_{i} | D \cap I) \\ = \frac{ℙ (A_{i} \cap D \cap I)}{ℙ (D \cap I)} \\ \leq \frac{ℙ (A_{i} \cap I)}{ℙ (D \cap I)} \\ = \frac{ℙ (A_{i}) ℙ (I)}{ℙ (D \cap I)} \\ = \frac{ℙ (A_{i})}{ℙ (D | I)} \end{array}

Let ${A_{i_{1}}, \dots, A_{i_{s}}}$ be the events in the intersection $D$ . Then

\begin{array}{l} ℙ (D | I) & = \prod_{j = 1}^{s} ℙ (A_{i_{j}}^{c} | I \cap A_{i_{1}}^{c} \cap \dots \cap A_{i_{j - 1}}^{c}) \\ = \prod_{j = 1}^{s} (1 - ℙ (A_{i_{j}} | I \cap A_{i_{1}}^{c} \cap \dots \cap A_{i_{j - 1}}^{c})) \end{array}

If no events in the intersection, then we are already done. Otherwise, we may apply the induction hypothesis to each term to get

\frac{ℙ (A_{i})}{ℙ (D | I)} \leq \frac{x_{i} \prod_{j \sim i} (1 - x_{j})}{\prod_{j = 1}^{s} (1 - x_{i_{j}})} \leq x_{i} . □

Proof of Lopsided Local Lemma. Apply Lopsided Local Lemma with weights $x_{i} = \frac{1}{Δ + 1}$ for all $i$ . We just need to check that the probability upper bounds in Lopsided Local Lemma hold.

By calculus, we have

{(\frac{Δ}{Δ + 1})}^{Δ} \geq \frac{1}{e} .

Hence

\begin{array}{l} ℙ (A_{i}) & \leq \frac{1}{e (Δ + 1)} \\ \leq \frac{1}{Δ + 1} {(\frac{Δ}{Δ + 1})}^{Δ} \\ = \frac{1}{Δ + 1} {(1 - \frac{1}{Δ + 1})}^{Δ} \\ \leq \frac{1}{Δ + 1} \prod_{A_{i} \sim A_{j}} (1 - \frac{1}{Δ + 1}) □ \end{array}

Now we will see another proof of $R (3, k) \geq c \frac{k^{2}}{{(\log k)}^{2}}$ (Theorem 3.1), in order to give some intuition as to what kind of situations are good for Local Lemma. Roughly speaking, it works well if your events are “weakly dependent”, or there are “not too many dependencies” among them.

Proof of $R (3, k) \geq c \frac{k^{2}}{{(\log k)}^{2}}$ using Lopsided Local Lemma. Recall that it is enough to show that for sufficiently large $n$ , there exists a triangle-free graph on $n$ vertices with $α (G) \leq C \sqrt{n} \log n$ (this was the statement of Theorem 3.2).

Set $k = C \sqrt{n} \log n$ , and sample $G \sim G (n, p)$ where $p = \frac{γ}{\sqrt{n}}$ , with $γ > 0$ is chosen later.

Define the events:

For each $T \in {[n]}^{(3)}$ , define
$A_{T} = “ T^{(2)} \subset G ” .$
For each $I \in {[n]}^{(k)}$ , define
$B_{I} = “ I independent in G ” .$

Define the dependency graph $G$ :

$A_{T} \sim A_{S}$ for $S, T \in {[n]}^{(3)}$ if $S^{(2)} \cap T^{(2)} \neq \emptyset$ .
$A_{T} \sim B_{I}$ for $T \in {[n]}^{(3)}, I \in {[n]}^{(k)}$ if $S^{(2)} \cap I^{(2)} \neq \emptyset$ .
$B_{I} \sim B_{J}$ for $I, J \in {[n]}^{(k)}$ if $I^{(2)} \cap J^{(2)} \neq \emptyset$ .

Now note:

The event $A_{T}$ is $\sim$ to $\leq 3 n$ $A_{S}$ , $S \in {[n]}^{(3)}$ .
The event $A_{T}$ is $\sim$ to $\leq 3 n^{k - 2}$ $B_{I}$ , $I \in {[n]}^{(k)}$ .
The event $B_{I}$ is $\sim$ to $\leq k^{2} n$ $A_{S}$ , $S \in {[n]}^{(3)}$ .
The event $B_{I}$ is $\sim$ to $\leq k^{2} n^{k - 2}$ $B_{J}$ , $J \in {[n]}^{(k)}$ .

We choose $x_{T} = 2 p^{3}$ for all $T \in {[n]}^{(3)}$ (“we want to make it a bit bigger than the probability of it occuring so that we can afford the product stuff”) and $x_{I} = n^{- 10 k}$ for all $I \in {[n]}^{(k)}$ .

Then

\begin{array}{l} x_{T} \prod_{\begin{array}{c} S \in {[n]}^{(3)} \\ T \sim S \end{array}} (1 - x_{S}) \prod_{\begin{array}{c} I \in {[n]}^{(k)} \\ I \sim T \end{array}} (1 - x_{I}) & \geq 2 p^{3} {(1 - 2 p^{3})}^{3 n} {(1 - n^{- 10 k})}^{3 n^{k - 2}} \\ \geq 2 p^{3} \exp (- (1 + o (1)) [2 p^{3} (3 n) + 3 n^{- 10 k} n^{k - 2}]) \\ = 2 p^{3} (1 + o (1)) \\ \geq p^{3} \end{array}

for large enough $n$ . We have $ℙ (B_{I}) = {(1 - p)}^{(\binom{k}{2})} \leq e^{- p (\binom{k}{2})}$ , so

\begin{array}{l} x_{I} {(1 - 2 p^{3})}^{k^{2} n} {(1 - n^{- 10 k})}^{k^{2} n^{k - 2}} & \geq n^{- 10 k} \exp (- (1 + o (1)) [2 p^{3} k^{2} n + \underset{\to 0}{\underset{⏟}{n^{- 10 k} k^{2} n^{k - 2}}}]) \\ = n^{- 10 k} \exp (- (1 + o (1)) (2 γ^{2}) p k^{2}) \end{array}

Note

e^{- p (\binom{k}{2})} = \exp (- \frac{γ}{\sqrt{n}} k C \sqrt{n} (\log n)) = n^{- γ C k} .

First choose $γ$ small so $e^{- 2 γ^{2} p k} ≫ e^{- p (\binom{k}{2}) \frac{1}{2}}$ , and then choose $C ≫ \frac{1}{γ}$ , then done. □