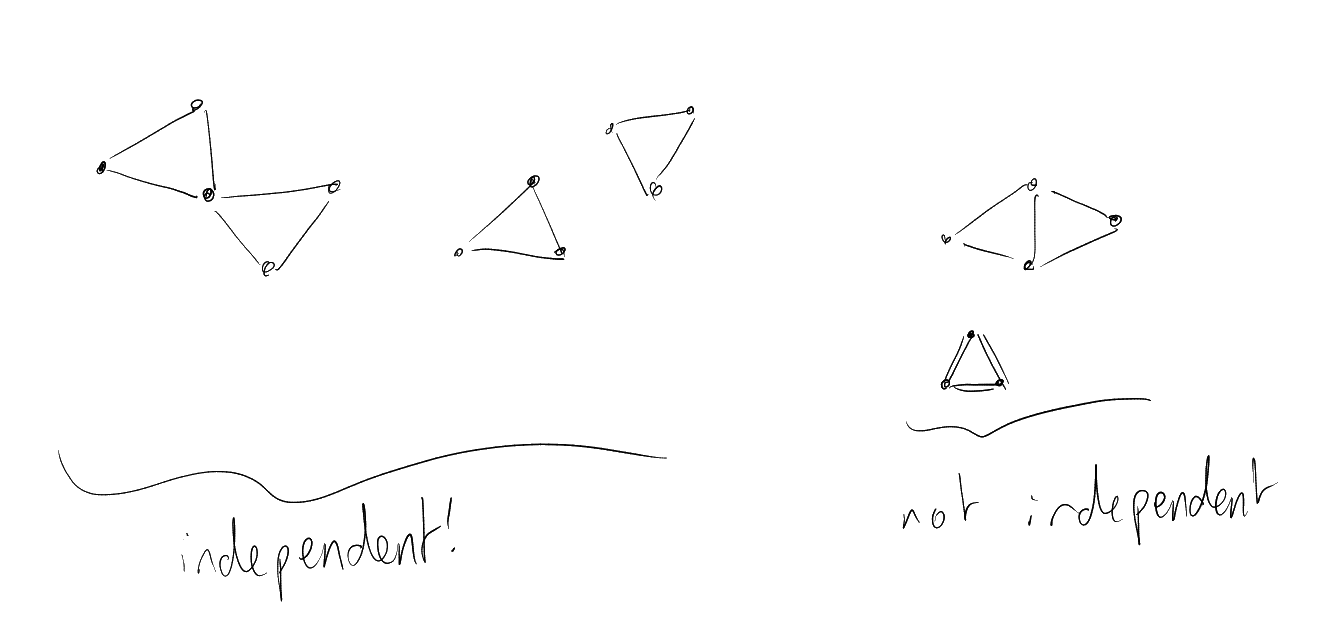The Ramsey numbers R(3,k) - Probabilistic Combinatorics

2 The Ramsey numbers $R (3, k)$

Theorem 2.1 (Erdos-Szekeres, 1935). $R (l, k) \leq (\binom{k + l - 2}{l - 1})$ .

Proof. Induction. □

Note. $R (k) = R (k, k) \leq (\binom{2 (k - 1)}{k - 1}) \sim c \frac{4^{k}}{\sqrt{k}}$ .

Corollary 2.2. $R (3, k) \leq k^{2}$ .

Idea 1: If randomly colour $K_{n}$ , we have $\sim \frac{1}{8} (\binom{n}{3})$ triangles $⇝$ :(

Idea 2: We want to bias our distribution in favour of $K_{k}$ – colour “red”. Say $G \sim G (n, p)$ . Sad news: if $p ≫ \frac{1}{n}$ then $G$ contains a $K_{3}$ with high probability. $⇝$ :(

Theorem 2.3 (Erdos, 1960s). $R (3, k) \geq c {(\frac{k}{\log k})}^{3 ∕ 2}$ for some $c > 0$ .

Proof idea: Sample $G \sim G (n, p)$ , then define $\tilde{G} = G - (a vertex from each triangle)$ . For this to work we need $\frac{# vertices}{2} > # triangles$ . So $\frac{n}{2} > p^{3} (\binom{n}{3})$ . So take $p \sim n^{- 2 ∕ 3}$ .

Remark. This is called the “deletion method”.

Fact (Markov). Let $X$ be a non-negative random variable. Let $t > 0$ . Then

ℙ (X \geq t) \leq \frac{𝔼 X}{t} .

That is

ℙ (X \geq s 𝔼 X) \leq \frac{1}{s},

for any $s > 0$ .

Fact. For $1 \leq k \leq n$ we have

(\binom{n}{k}) \leq {(\frac{e n}{k})}^{k}

and

(\binom{n}{k}) \geq {(\frac{n}{k})}^{k} .

Definition 2.4 (Independence number). Let $G$ be a graph. Then $I \subset V (G)$ is independent if $x ⁄ \sim y$ in $G$ for all $x, y \in I$ .

Let $α (G) = size of the largest independent set$ .

Note. To prove Theorem 2.3, we are trying to construct a triangle free graph on $k^{3 ∕ 2 - o (1)}$ vertices with $α (G) < k$ .

Lemma 2.5. Assuming that:

$\frac{1}{n} ≪ p \leq \frac{1}{2}$
$G \sim G (n, p)$

Then

α (G) \leq (2 + o (1)) \frac{\log n p}{p},

with probability tending to $1$ as $n \to \infty$ (known as “with high probability (w.h.p.)”).

Remark. We actually have $=$ in this lemma.

Proof. Let $k = (2 + δ) \frac{\log n p}{p}$ , for some $δ > 0$ . Let $X$ be the random variable that counts the number of independent $k$ sets in $G$ . Using $1 - x \leq e^{- x}$ ,

\begin{array}{l} 𝔼 X & = 𝔼 \sum_{I \in {[n]}^{(k)}} 𝟙_{I is independent} \\ = \sum_{I \in {[n]}^{(k)}} ℙ (I is independent) \\ = (\binom{n}{k}) {(1 - p)}^{(\binom{k}{2})} \\ \leq {(\frac{e n}{k})}^{k} e^{- p (\binom{k}{2})} \\ = {(\frac{e n}{k} \cdot e^{- (\frac{k - 1}{2}) p})}^{k} \\ \to 0 \end{array}

by plugging in $k$ . So by Markov,

ℙ (X \geq 1) \leq 𝔼 X \to 0 . □

We have a method for bounding the probability that $X$ is large: Markov says that $ℙ (X > t) \leq \frac{𝔼 X}{t}$ . What about bounding the probability that it is small?

Fact: Let $X$ be a random variable with $𝔼 X$ , $Var X$ finite. Then for all $t > 0$ ,

ℙ (| X - 𝔼 X | \geq t) \leq \frac{Var X}{t^{2}} .

Reminder:

Var X = 𝔼 X^{2} - {(𝔼 X)}^{2} = 𝔼 {(X - 𝔼 X)}^{2} .

Lemma 2.6. Assuming that:

$\frac{1}{n} ≪ p \leq 1$
$G \sim G (n, p)$

Then

# triangles in G = (1 + o (1)) p^{3} (\binom{n}{3})

with high probability.

Proof. Let $X$ be the random variable counting the number of triangles in $G$ . Note

X = \sum_{T \in {[n]}^{(3)}} 𝟙_{T^{(2)} \subset G} .

Mean is straightforward:

𝔼 X = p^{3} (\binom{n}{3}) .

Variance is a little more tricky. First:

X^{2} = \sum_{S, T \in {[n]}^{(3)}} 𝟙_{S^{(2)}, T^{(2)} \subset G} .

We can write

\begin{array}{l} 𝔼 X^{2} & = \sum_{S, T \in {[n]}^{(3)}} ℙ (T^{(2)}, S^{(2)} \subset G) \\ {(𝔼 X)}^{2} & = \sum_{S, T \in {[n]}^{(3)}} ℙ (T^{(2)} \subset G) ℙ (S^{(2)} \subset G) \end{array}

Since the pairs of events are independent whenever $| S^{(2)} \cap T^{(2)} | = 0$ , and since $| S^{(2)} \cap T^{(2)} | = 2$ is impossible, we have

\begin{array}{l} Var X & \leq \sum_{\begin{array}{c} S, T \in {[n]}^{(3)} \\ | S^{(2)} \cap T^{(2)} | = 1 \end{array}} ℙ (S, T \subset G) + \sum_{\begin{array}{c} S, T \in {[n]}^{(3)} \\ | S^{(2)} \cap T^{(2)} | = 3 \end{array}} ℙ (S, T \subset G) \\ = p^{5} n^{4} + 𝔼 X \end{array}

Now note

\begin{array}{l} ℙ (| X - 𝔼 X | \geq δ 𝔼 X) & \leq \frac{Var X}{δ^{2} {(𝔼 X)}^{2}} \\ \leq \frac{p^{5} n^{4}}{δ^{2} {(𝔼 X)}^{2}} + \frac{1}{δ^{2} 𝔼 X} \\ \leq C \frac{p^{5} n^{4}}{{(n^{3} p^{3})}^{2}} + \frac{1}{δ^{2} 𝔼 X} \\ \leq C \frac{1}{n^{2} p} + \frac{1}{δ^{2} 𝔼 X} \\ \to 0 □ \end{array}

Recall: In Lemma 2.5 we showed that for $G \sim G (n, p)$ , $\frac{1}{n} ≪ p \leq \frac{1}{2}$ , we have

α (G) \leq (2 + o (1)) \frac{\log (n p)}{p}

with high probability.

Proof of Theorem 2.3, a lower bound on $R (3, k)$ . Set $n = {(\frac{k}{2 \log k})}^{3 ∕ 2}$ , $p = n^{- 2 ∕ 3} = \frac{2 \log k}{k}$ . Let $G \sim G (n, p)$ and let $\tilde{G}$ be $G$ with a vertex deleted from each triangle. Then clearly $α (\tilde{G}) \leq α (G)$ , so with high probability we have

\begin{array}{l} α (\tilde{G}) & \leq α (G) \\ \leq (2 + o (1)) \frac{\log n p}{p} \\ \leq (\frac{2}{3} + o (1)) n^{2 ∕ 3} \log n \\ \leq (\frac{2}{3} + o (1)) \frac{k}{2 \log k} (\log k^{3 ∕ 2}) \\ \leq (1 + o (1)) \frac{k}{2} \\ < k & (*) \end{array}

We also have with high probability:

\begin{array}{l} | V (\tilde{G}) | & \geq n - (# of triangles in G) \\ \geq n - (1 + o (1)) \frac{p^{3} n^{3}}{6} \\ = n - (1 + o (1)) \frac{n}{6} \\ \geq \frac{n}{2} & (* *) \end{array}

So with high probability ( $*$ ) and ( $* *$ ) hold (if ( $*$ ) holds with probability at least $1 - 𝜀_{1}$ and ( $* *$ ) holds with probability at least $1 - 𝜀_{2}$ , then the probability that they both hold is at least $1 - 𝜀_{1} - 𝜀_{2} \to 1$ ). So there must exist a graph $\tilde{G}$ on $\frac{n}{2} = \frac{1}{2} {(\frac{k}{2 \log k})}^{3 ∕ 2}$ vertices with no triangles and independence number $< k$ . □

Definition (Chromatic number). Let $G$ be a graph. The chromatic number of $G$ is the minimum $k$ such that there exists $χ : V (G) \to [k]$ such that no edge has both ends in the same colour.

$χ (G)$ denotes the chromatic number.

Definition 2.7 (Girth). The girth of a graph $G$ is the length of the shortest cycle in $G$ .

Using a method similar to the proof of Theorem 2.3 that we just saw, Erdős proved:

Theorem (Erdős). There exist graphs $G$ with arbitrarily large chromatic number and arbitrarily large girth, i.e. for all $g, k \in ℕ$ there exists $G$ with girth $> g$ and $χ (G) > k$ .

This theorem is somewhat surprising, because if you think of examples of graphs with large chromatic number, the first things you try have small girth (for example, $K_{n}$ ). It shows that the answer to the question “what kind of necessary conditions are there for chromatic number to be large?” is not so simple.

2 The Ramsey numbers R(3,k)

2 The Ramsey numbers $R (3, k)$