An edge deletion method - Probabilistic Combinatorics

3 An edge deletion method

In this section, we’ll improve the lower bound on $R (3, k)$ that we proved in Theorem 2.3.

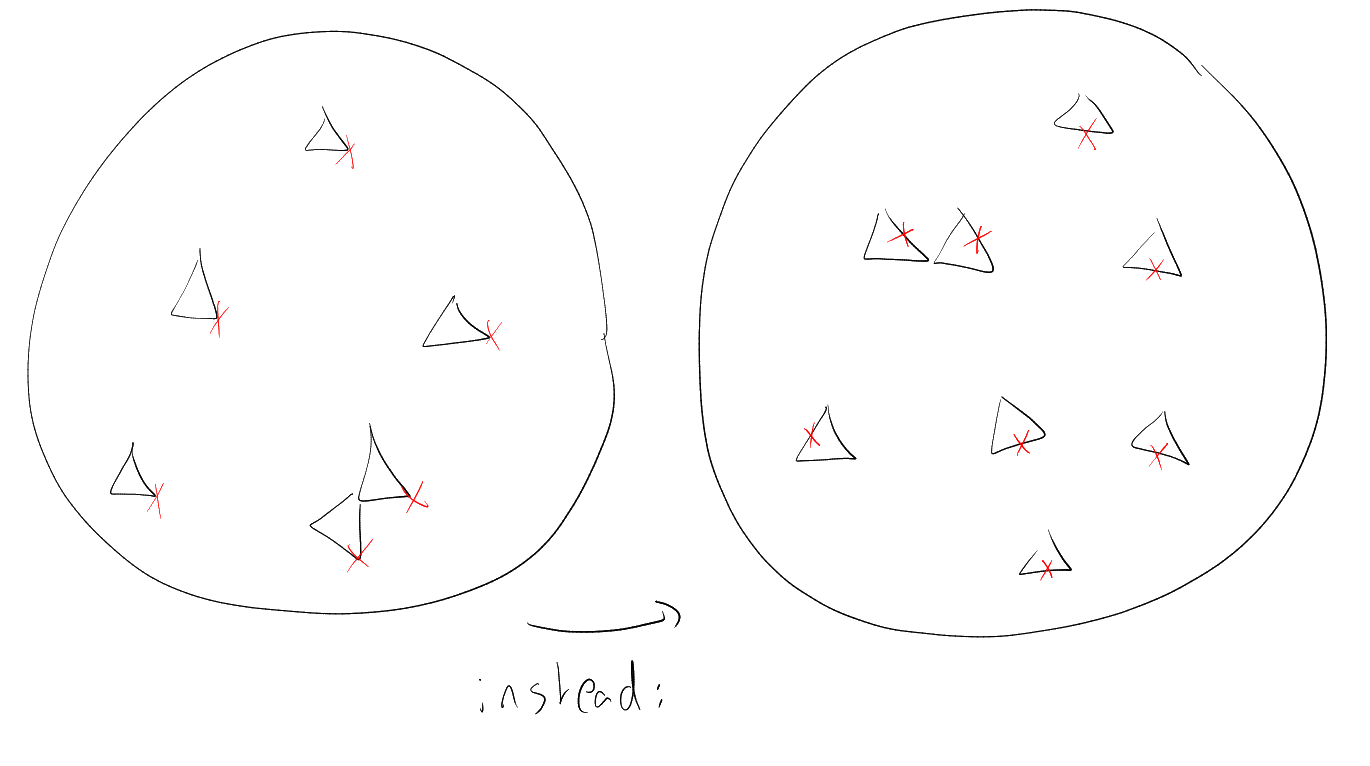
Idea: let’s delete an edge from each triangle, instead of a vertex (we have a lot more edges to spend than we have vertices!). “The vertex set is our most expensive real estate.”

For this we want

p^{3} n^{3} ≪ p n^{2}

so $p = \frac{γ}{\sqrt{n}}$ . For some small $γ > 0$ .

Danger: when we delete an edge from each triangle, we need to ensure that we don’t hurt $α (G)$ .

Theorem 3.1 (Erdos, 1960s). $R (3, k) \geq c \frac{k^{2}}{{(\log k)}^{2}}$ for some $c > 0$ .

Since we already saw $R (3, k) \leq k^{2}$ in Corollary 2.2 (which followed from Erdos-Szekeres, 1935), this theorem now tells us the polynomial order of $R (3, k)$ (up to poly-logs).

To prove this, it is enough to prove the following:

Theorem 3.2. There exists a constant $C$ such that for all $n \geq 2$ , there exists a triangle-free graph $G$ on $n$ vertices with

α (G) \leq C \sqrt{n} \log n .

Proof of Theorem 3.1 from Theorem 3.2. Set $k = C \sqrt{n} \log n$ , and then get $n = c \frac{k^{2}}{{(\log k)}^{2}}$ . □

When proving Theorem 3.2, note that we only have to prove it for large $n$ , because then we can just adjust our value of $C$ to make the result also true for small $n$ .

Now we sketch the idea of Theorem 3.2: we know $α (G) \leq 2 \frac{\log n}{p}$ .

What if $k > 2 \frac{\log n p}{p}$ ? Then there must be an edge (because $α (G) < k$ .

Not very impressive.

What if $k > 100 \frac{\log n p}{p}$ ? Then we actually get a lot of edges: expect $p k^{2}$ , and can guarantee $\frac{p k^{2}}{16}$ .

Lemma 3.3. Assuming that:

$\frac{1}{n} ≪ p \leq \frac{1}{2}$
$G \sim G (n, p)$
$k > C \frac{\log n}{p}$

Then with high probability every set of size

\geq k

G

induces at least

\frac{p k^{2}}{16}

edges.

This lemma will be used to show that we can delete an edge from every triangle without increasing the independence number of our graph too much, but we will see later that a small trick is needed before we can apply this.

Proof. Fix $t = \frac{p k^{2}}{16}$ and fix a set $S$ with size $| S | = k$ .

\begin{array}{l} ℙ (e (G [S]) < t) & \leq \sum_{i = 0}^{t} (\binom{(\binom{k}{2})}{i}) p^{i} {(1 - p)}^{(\binom{k}{2}) - i} \\ \leq t (\binom{(\binom{k}{2})}{t}) p^{t} {(1 - p)}^{(\binom{k}{2}) - t} \\ \leq t [{(\frac{e k^{2}}{2 t})}^{t} p^{t}] e^{- p [(\binom{k}{2}) - t]} \\ \leq t {(e 8)}^{\frac{p k^{2}}{16}} e^{- p (\binom{k}{2}) ∕ 2} \\ \leq k^{2} {[{(e 8)}^{1} e^{- 4 + o (1)}]}^{\frac{p k^{2}}{16}} \\ \leq e^{- α p k^{2}} \end{array}

for some $α > 0$ .

We now union bound over all $S \in {[n]}^{(k)}$ .

\begin{array}{l} ℙ (\exists S \in {[n]}^{(k)} such that e ([S]) < t) & \leq (\binom{n}{k}) ℙ (e (G [S]) < t) \\ \leq {(\frac{e n}{k})}^{k} e^{- α k^{2} p} \\ = {(\frac{e n}{k} \cdot e^{- α k p})}^{k} \\ \leq {(e n p {(\frac{1}{p n})}^{α C})}^{k} \end{array}

(using $k p \geq C \log n$ ) which $\to 0$ for $C > \frac{1}{α}$ . □

Lemma 3.4. Assuming that:

$F = {A_{i}}_{i}$ be a collection of events
let $E_{t}$ , for $t \in ℕ$ , be the event that $t$ independent events of $F$ occur

Then

ℙ (E_{t}) \leq \frac{1}{t!} {(\sum_{i} ℙ (A_{i}))}^{t} .

Remark. $t! = t^{t} e^{- t} \sqrt{2 π t} (1 + o (1))$ .

Using $t! \geq t^{t} e^{- t} ∕ 2$ for large $t$ in the above lemma, we get:

ℙ (E_{t}) \leq 2 {(\frac{e 𝔼 (# of A_{i} that hold}{t})}^{t} .

Proof. Let $I = {(A_{i_{1}}, \dots, A_{i_{k}}) : A_{i_{1}}, \dots, A_{i_{k}} are independent}$ .

\begin{array}{l} 𝟙_{E_{t}} & \leq \frac{1}{t!} \sum_{(A_{i_{1}}, \dots, A_{i_{k}}) \in I} 𝟙_{A_{i_{1}} \cap \dots \cap A_{i_{k}}} \\ ℙ (E_{t}) & \leq \frac{1}{t!} \sum_{(A_{i_{1}}, \dots, A_{i_{k}}) \in I} ℙ (A_{i_{1}} \cap \dots \cap A_{i_{k}}) \\ = \frac{1}{t!} \sum_{(A_{i_{1}}, \dots, A_{i_{k}}) \in I} ℙ (A_{i_{1}}) \dots ℙ (A_{i_{k}}) \\ \leq \frac{1}{t!} \sum_{i_{1}, \dots, i_{t}} ℙ (A_{i_{1}}) \dots ℙ (A_{i_{k}}) \\ = \frac{1}{t!} {(\sum_{i} ℙ (A_{i}))}^{t} □ \end{array}

Proof of Theorem 3.2. Let $n$ be large. Let $p = \frac{γ}{\sqrt{n}}$ for some $γ > 0$ . Let $G \sim G (n, p)$ .

Here comes a smart idea: instead of deleting an edge from every triangle in an arbitrary way, we will do it in a slightly smarter way.

Let $T$ be a maximal collection of edge disjoint triangles in $G$ , and let $\tilde{G} = G - T$ . By maximality of $T$ , $\tilde{G}$ is triangle-free.

We’ll see shortly that adding this little bit of structure is very helpful for making the proof go through (i.e. the proof that the independence number is still large).

To show that the independence number of $\tilde{G}$ is large, we will do a common and useful kind of manoeuvre. We want to take a big union bound over all independent sets, but this union bound only works if we can show that all the individual events occur with low enough probability to “beat out” the count of the number of events that we take a union over.

If the events are somewhat or very correlated, then we are very much at risk of the sum of probabilities being large, because we might be overcounting by too much.

In this case, we will get around the issue by introducing a quasirandomness property $Q$ that holds with high probability, and has the nice property that the events become less correlated if we condition on $Q$ . Then we will be able to apply a union bound by conditioning on $Q$ .

So we will “prepare globally, then zoom in locally”.

We let $Q$ be the event that every set of size $k$ , where $k = C \sqrt{n} \log n$ , contains at least $\frac{p k^{2}}{16}$ edges. By Lemma 3.3, $Q$ occurs with high probability. We now consider

ℙ (α (\tilde{G}) \geq k) = ℙ (α (\tilde{G}) \geq k \cap Q) + ℙ (α (\tilde{G}) \geq k \cap Q^{c}) .

ℙ (α (\tilde{G}) \geq k) \leq \underset{(*)}{\underset{⏟}{ℙ (α (\tilde{G}) \geq k \cap Q)}} + o (1) .

We now union-bound

\begin{array}{l} (*) & \leq (\binom{n}{k}) ℙ (I independent in \tilde{G} \cap Q) \\ \leq (\binom{n}{k}) ℙ (T intersects I in \geq \frac{p k^{2}}{16} edges) \\ = (* *) \end{array}

Define ${T_{i}}$ to be the collection of all triangles that meet $I$ in at least one edge, and define the event $A_{i} = {T_{i} \subset G}$ .

Note that the event $E_{t}$ , where $t = \frac{p k^{2}}{16}$ , from the lemma holds on the event that $T$ meets $I$ in $\frac{p k^{2}}{16}$ edges. This is where we use the fact that we only choose edge-disjoint triangles! By Lemma 3.4, we have

\begin{array}{l} ℙ (E_{t}) & \leq 2 {(\frac{e k^{2} n p^{3}}{t})}^{t} \\ \leq {(\frac{16 e k^{2} n p^{3}}{p k^{2}})}^{\frac{p k^{2}}{16}} \\ = {(16 e γ^{2})}^{\frac{p k^{2}}{16}} \end{array}

(* *) \leq {(16 e γ^{2})}^{\frac{p k^{2}}{16}} {(\frac{e n}{k})}^{k} \to 0,

if $γ$ is chosen to be small and $C$ large. □