1 Estimating Primes
Theorem (Euler).
.
Proof.
Consider ,
for . We
have:
On the other hand, using ,
so
Comparing these two bounds gives
|
|
Then letting
gives the desired result. □
Theorem (Chebyshev’s Theorem).
(for ,
where
is an absolute constant).
Proof.
Consider
for . We
have
On the other hand,
where is
the largest
such that .
We have for
. So
Take ,
for .
Hence
|
|
Then
So for and a suitable
large enough constant ,
we have
|
|
Hence
for any , as
long as .
Take .
Choose
large enough. □
1.1 Asymptotic Notation
Definition 1.1 (Big and little notation).
Let ,
.
Write
if there is
such that
for all .
Write
if for any
there is
such that
for ,
.
Write
if
and write
if .
Definition 1.2 (Vinogradov notation).
Let ,
.
Write
or
if .
Example.
-
(),
since ,
.
-
(for ).
-
for ,
since .
-
for
(since ).
-
(for ).
Lemma.
Let .
-
(i)
If
and ,
then
(transitivity).
-
(ii)
If
and ,
then .
-
(iii)
If
and ,
then .
Proof.
Follows from the definition in a straightforward way. Example:
-
(iii)
,
.
Then ,
so .
□
1.2 Partial Summation
Lemma 1.3 (Partial Summation).
Assuming that:
Then |
|
where for ,
we define
Proof.
It suffices to prove the
case, since then
|
|
Suppose .
By the fundamental theorem of calculus,
|
𝟙 |
Summing over ,
we get
𝟙
Lemma.
If ,
then
where is Euler’s constant,
which is given by .
Proof.
Apply Partial Summation with ,
,
. Clearly
.
Then,
The last equality is true since .
Let .
Then we have the asymptotic equation as desired.
Taking in the
formula, we see that
is equal to the formula for Euler’s constant, as desired. □
Proof.
Apply Lemma 1.3 with 𝟙
(where
is the set of primes), ,
and .
We get ,
and then
1.3 Arithmetic Functions and Dirichlet convolution
Definition (Arithmetic function).
An arithmetic function is a function .
Definition (Multiplicative).
An arithmetic function
is multiplicative if
and
whenever
are coprime.
Moreover,
is completely multiplicative if
for all .
On the space of arithmetic functions, we have operations:
Definition (Dirichlet convolution).
For ,
we define
where
means sum over the divisors of .
Proof.
Since arithmetic functions with
form an abelian group, it suffices to show:
-
(i)
-
(ii)
-
(iii)
-
(iv)
Proofs:
Proof.
Need
such that .
|
|
Assume defined
for . We will
defined .
Proof.
For the first part, suffices to show closedness. Let
be multiplicative, and
coprime.
If , we can
write ,
where
,
,
and
.
Therefore we have:
(also need to check that inverses are multiplicative).
Now, remains to show that for completely multiplicative
,
.
Note that is multiplicative by the
first part. So enough to show
for prime powers .
Calculate:
and for :
Example.
.
Then
So is
multiplicative by the previous result.
Definition (von Mangoldt function).
The von Mangoldt function
is
|
|
Then
since
|
|
Since is the
inverse of ,
we have
|
|
1.4 Dirichlet Series
For a sequence ,
we want to associate a generating function that gives information of
. Might
consider
If we do this, then
is hard to control. So this is not very useful.
The following series has nicer number-theoretic properties:
Definition (Formal series).
For ,
define a (formal) series
for .
Lemma.
Assuming that:
Then converges absolutely
for
and defines an
analytic function for
.
Proof.
Let
(fixed),
and .
Then
Hence we have absolute convergence for .
Also, is a uniform
limit of the functions .
From complex analysis, a uniform limit of analytic functions is analytic. Hence
is analytic
for .
Now let .
□
Theorem (Euler product).
Assuming that:
Proof.
Let ,
. Let
|
|
Note that the series defining the factors are absolutely convergent, since
|
|
(geometric series).
Therefore, multiplying out,
|
|
where
|
|
The fundamental theorem of arithmetic tells us that
and
for .
Now,
(since ).
Hence .
Finally, for
completely multiplicative, use geometric formula:
|
|
Lemma.
Assuming that:
-
-
Proof.
We know
and are
absolutely convergent, so can expand out the product.
Definition (Riemann zeta function).
For ,
define
Example.
-
for
(since ).
-
for
(since
is the Dirichlet inverse of ,
so ).
-
for ,
since .
Can differentiate termwise, since if
analytic and
uniformly, then
is analytic and .
We know that
converges uniformly for
if .
-
for .
This is because
– see the definition of the von Mangoldt function.
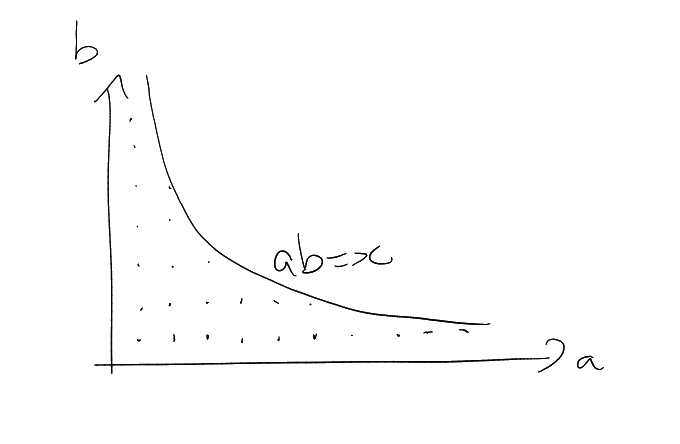
Dirichlet hyperbola method
Problem: How many lattice points
satisfy ?
Note that this number is .
Dirichlet proved that for ,
|
|
where
is Euler’s constant.
We will see a proof of this shortly.
Conjecture: Can have .
Current best exponent is .
First, we prove a lemma:
Lemma (Dirichlet hyperbola method).
Assuming that:
Then |
|
Proof.
.
Split this sum into parts with
and
to get the conclusion. □
Theorem 1.5 (Dirichlet’s divisor problem).
For
,
|
|
where
is Euler’s constant.
Proof.
We use the Dirichlet hyperbola method, with
. Note
that .
Then,
Recall from Lecture 2 that
Taking ,
the previous expression becomes
|
|