9 Ramsey–Turán
Theorem 9.1 (Turán).
Assuming that:
Then
In other words,
|
|
Example:
Definition 9.2 (Ramsey–Turán number).
Let
be a graph. Then we define
|
|
Example.
,
since the neighbourhood of every vertex must be an independent set (using the fact that we are triangle-free).
Theorem 9.3 (Szemerédi).
.
This was shown to be sharp by Bollobás and Erdős.
Theorem 9.4.
For every ,
there exists
such that if
and is
-free, we
have
Proof.
Given ,
let
and
and apply Szemerédi Regularity Lemma with parameters
and .
We define the graph on vertex set .
Define the reduced graph
on
and
if ,
-uniform
and .
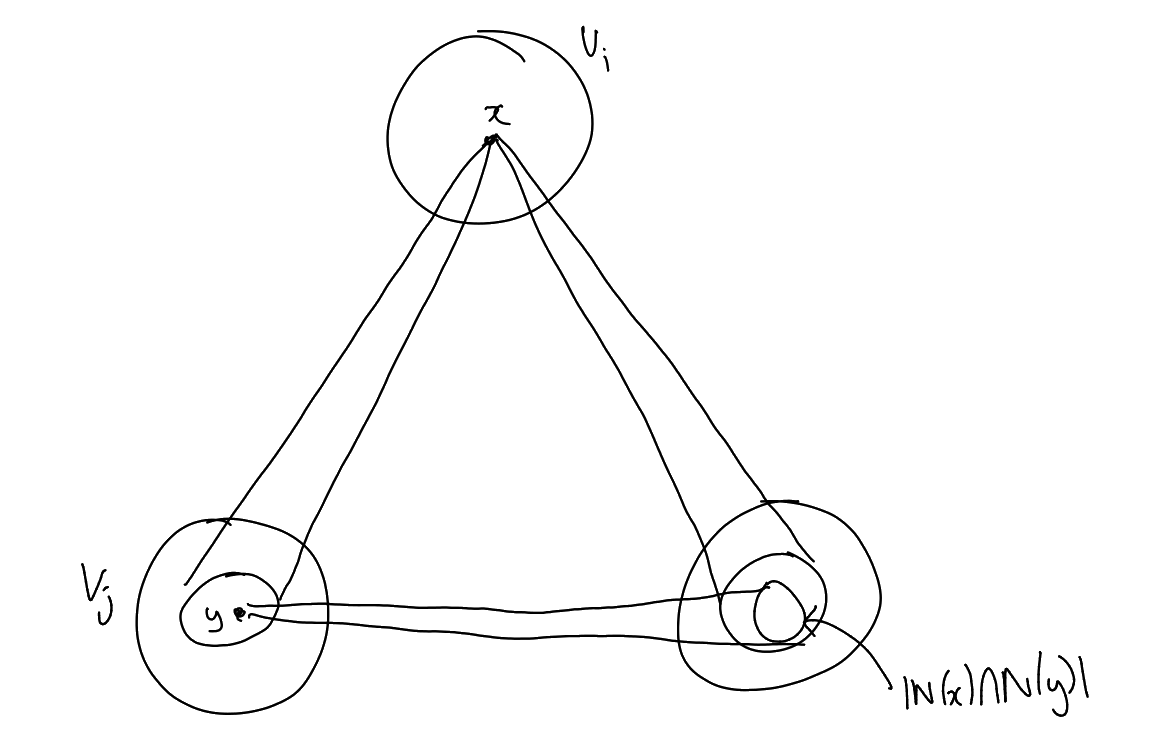
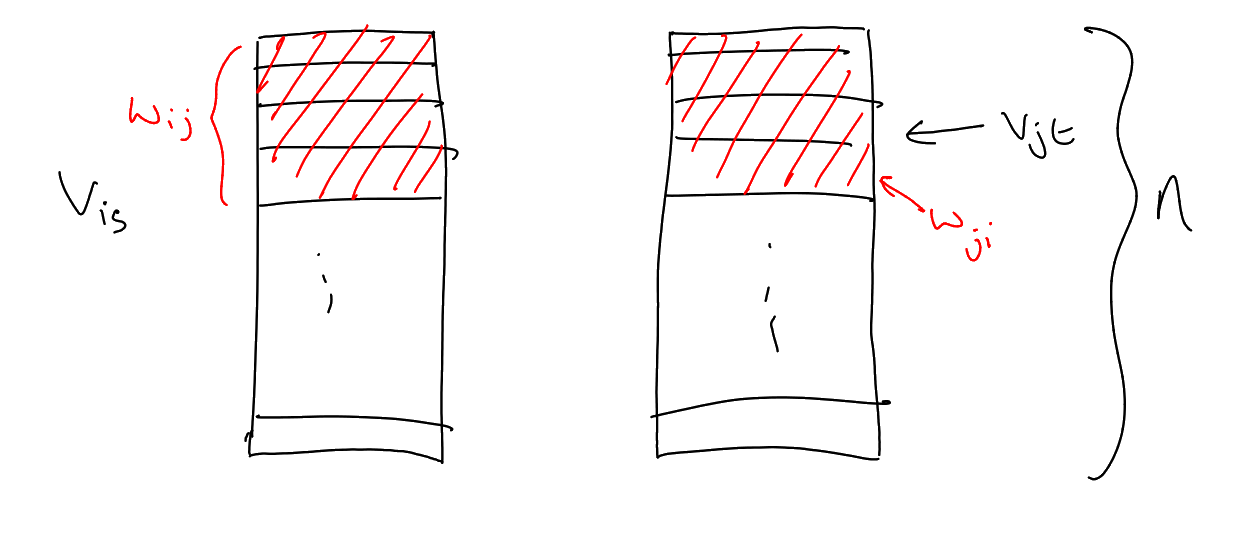
Claim 1:
is triangle-free.
If there exist
distinct with
|
|
and are pairwise -uniform.
Then consider
|
|
We know
so let .
Now let
|
|
Again this set is non-empty, so choose
in it.
So now note,
|
|
So there exist
such that .
But then
form a ,
contradiction.
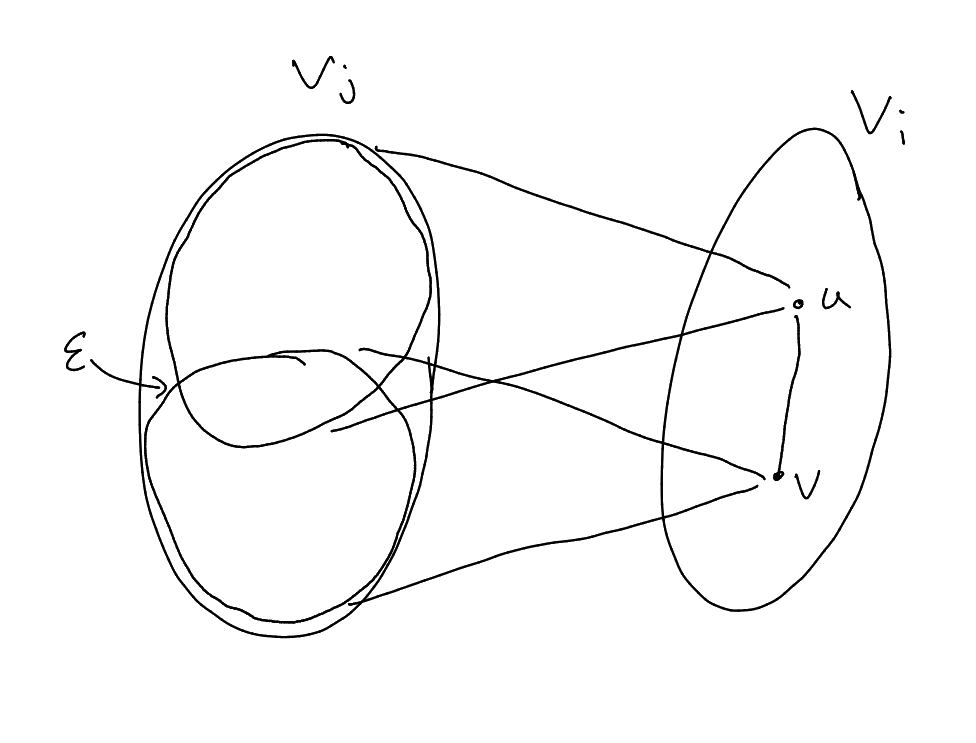
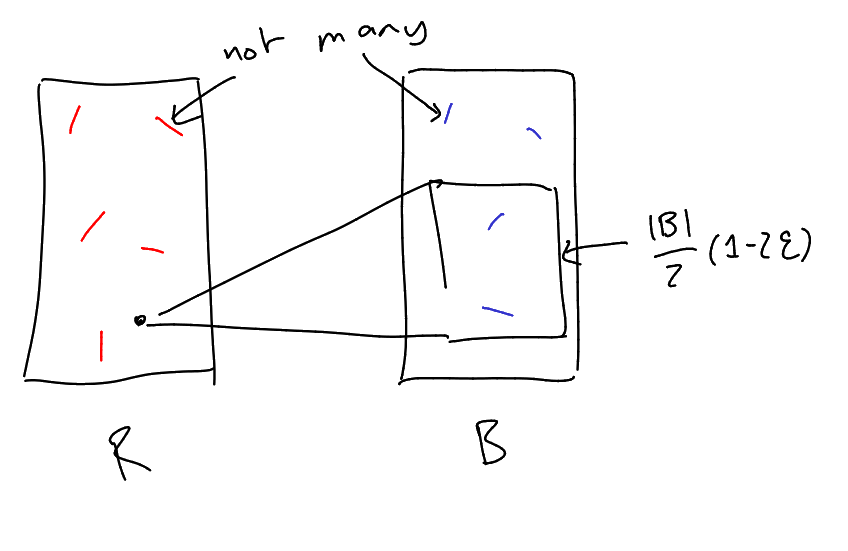
Claim 2: ,
for all .
Throw away
vertices in
with degree
to . There are at
least vertices
that remain in .
So there exist ,
.
Now note
Now use independence number property to find
such that .
Then is
a ,
contradiction.
We now estimate the number of edges in
using the claims.
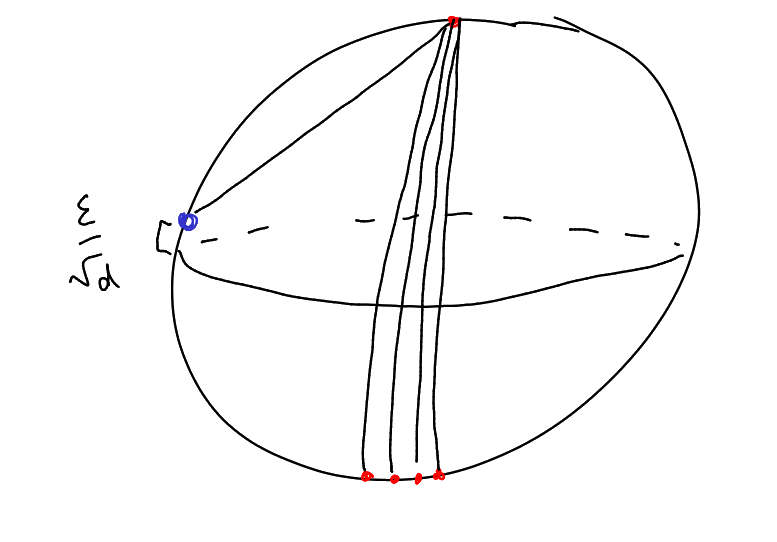
Theorem 9.5 (Bollobás–Erdős, 1970s).
There exists a graph
on
vertices
with ,
and
.
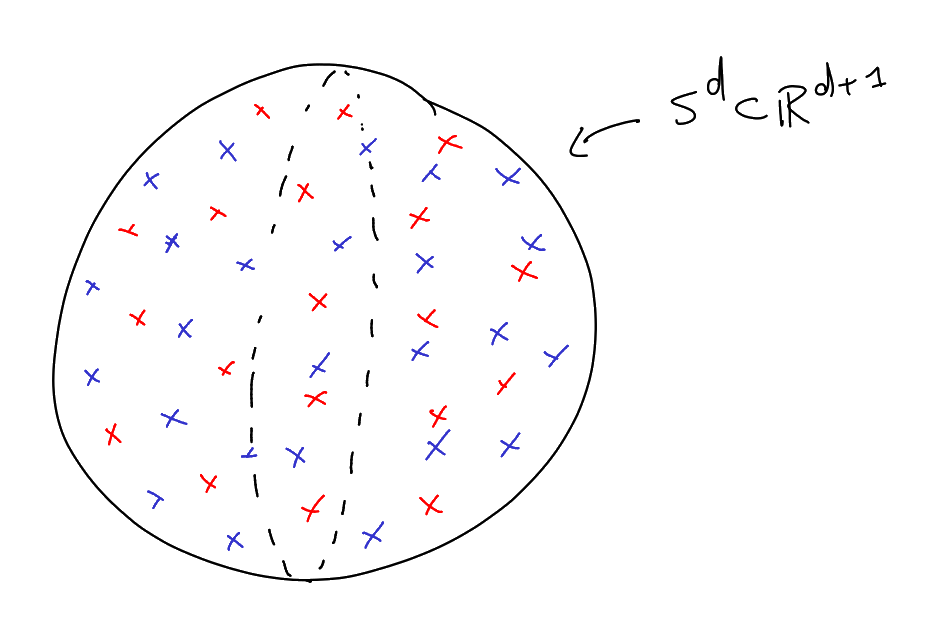
Sketch.
Let
slowly as . We
consider the sphere
in
dimensions.
“join a red point to a blue point if they are reasonably close” (say having inner product
bigger than some small quantity). “join red to red and join blue to blue if they have distance
.
A little more formally:
Let slowly,
and let
slowly.
-
Partition
into
regions of equal measure and with diameter .
-
Let ,
be a set of points, with one from each of these regions.
We define
by
-
,
:
when .
-
:
when .
-
Same for
Properties:
-
.
iff
. Let’s
imagine .
,
. So
()
is
, where
. So every vertex
has degree ,
so .
-
Now we check it is -free
First note are
triangle-free. Let and
assume they form a .
Then
Contradiction.
is
-free:
consider
where
and .
-
Finally, we need to check .
Let be independent.
Let , and without
loss of generality say .
Let
where
are the regions that we broke the sphere into at the start. We have
(where
is such
that ).
Note
with diameter
Fact from life: this implies
as .
Hence ,
i.e. .
□
What is the number of triangle-free graphs on
vertices?
Theorem 9.6 (Erdős, Klietman, Rothchild, 70s).
The number of triangle-free graphs on
vertices
is .
Remark.
“” comes from
considering all subgraphs of .
Can sort of think of this as saying ‘almost all triangle-free graphs are bipartite’.
Lemma 9.7.
For every
and large enough, there
exists a family of graphs
on with
the following properties:
-
(1)
.
-
(2)
All
can be made triangle-free by removing
edges.
-
(3)
Every triangle-free graph on
is contained in some .
Proof of Lemma 9.7.
Given a graph
on
and a partition ,
we define
to be the blow up of
onte
by
and include all of
into
whenever .
Let be given. We define
to be all graphs formed in
the following steps. Let .
-
(1)
Let
be a triangle-free graph on
where .
-
(2)
Let
be an equipartition, and blow up
onto .
-
(3)
Throw in
edges in any way.
Check
is small:
|
|
Each can be made
triangle-free by removing
edges: this is true by construction (in fact only need to remove
edges).
Finally, we need to check that every triangle-free graph on
is contained in some
. We apply Szemerédi Regularity
Lemma with parameter ,
, to get a
partition with
. Consider the
reduced graph .
Note is
triangle-free. So use
blown up to
plus
extra edges. □
Reminder of Szemerédi Regularity Lemma:
Theorem 9.8 (Regularity Lemma).
For ,
, there exists
such that the following
holds: Let be a graph. Then
there exists an equipartition
with , where
equipartition
and all but
pairs are
-uniform.
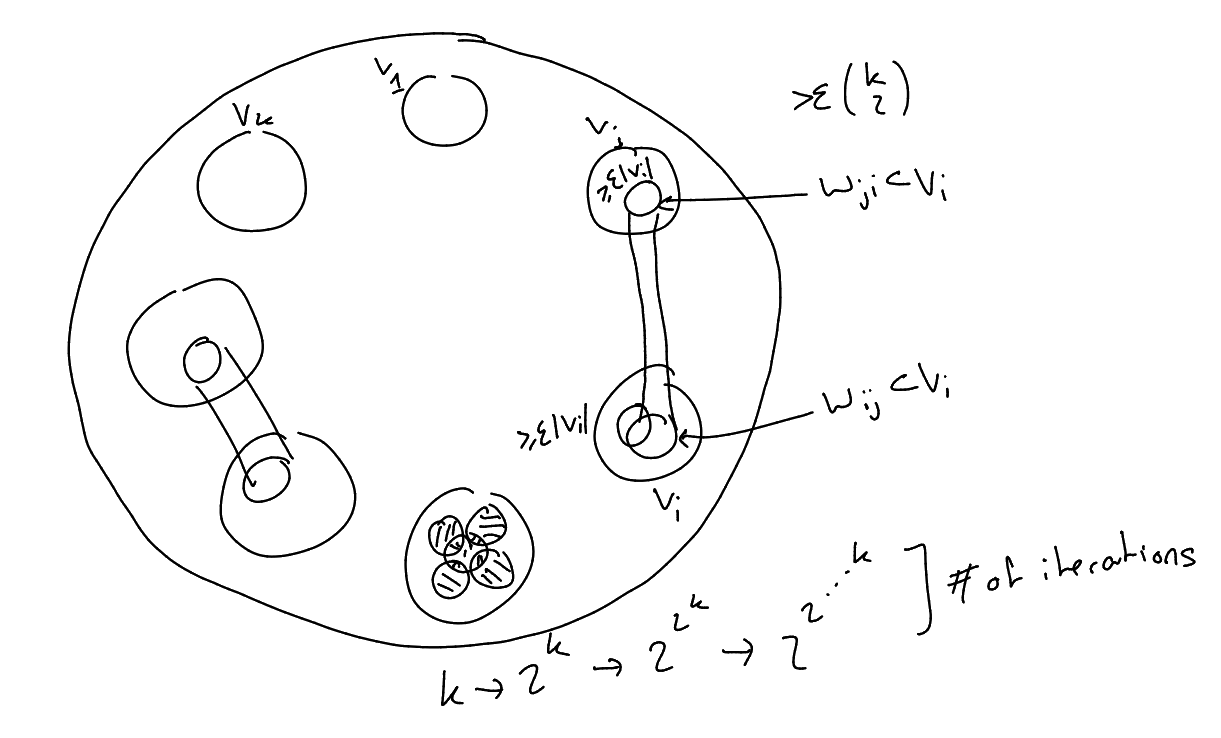
Proof of Szemerédi Regularity Lemma.
Given
and a graph ,
we loop the following, iteratively refining a partition.
Start with ,
arbitrarily into an equipartition. At a general step, we are given
an equipartition.
If there are
non -uniform
pairs, then output
and done So assume .
For each non -uniform
pair ,
we select ,
,
and .
Now for each
consider .
Let
be a common refinement of these .
We now refine this partition further to an equipartition where each cell has size
(this is a
slight cheat ).
Putting all these partitions together, we get
Now loop again with this partition.
Next step: show that this loop eventually terminates.
Analysis of Algorithm: We define the index of a partition
to be
We claim that as we go from
to , we increase the
index by at least .
Fix ,
and
consider
Here we are using
|
|
Note . Now
assume that ,
are not
-uniform.
Define
So
So since the number of non -uniform
pairs is , we
get an
boost from
proportion of the parts. Also, the other pairs don’t hurt us. So index increases by
.
How to fix the tiny lie at :
We can assume that we start the algorithm with
parts. Now each time we encounter a “rounding issue”, we just throw out the remainder of the cell to some
bin I track. At a given step, we throw out at most
Summing over all steps in algorithm, we still throw out at most
. We
just redistribute these vertices equally at the end.