Szemerédi Regularity Lemma - Probabilistic Combinatorics

8 Szemerédi Regularity Lemma

Informal statement

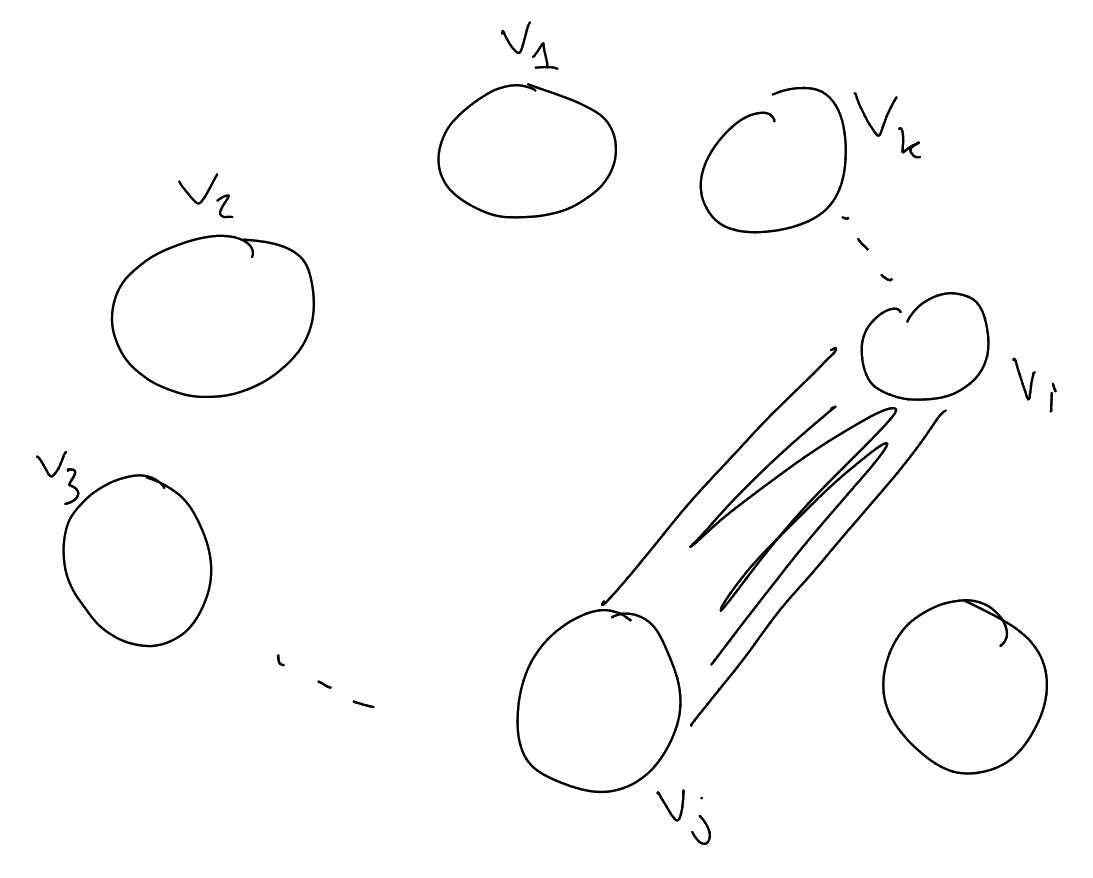
Let $G$ be a graph, $e (G) = α n^{2}$ . We can partition $V (G)$ into equal parts

V (G) = V_{1} \cup \dots \cup V_{k}

where $k \leq L (𝜀)$ depends only on a “coarseness” parameter $𝜀 > 0$ , so that for all but $𝜀 (\binom{k}{2})$ pairs $1 \leq i < j \leq k$ , the graph between $V_{i}$ , $V_{j}$ “looks” quasi-random.

So, in a sense, “every graph is somewhat random”.

Definition 8.1 (Edge density). Let $G$ be a graph. Let $U, V \subset V (G)$ . First define

d (U, V) = \frac{e (U, V)}{| U | | V |} .

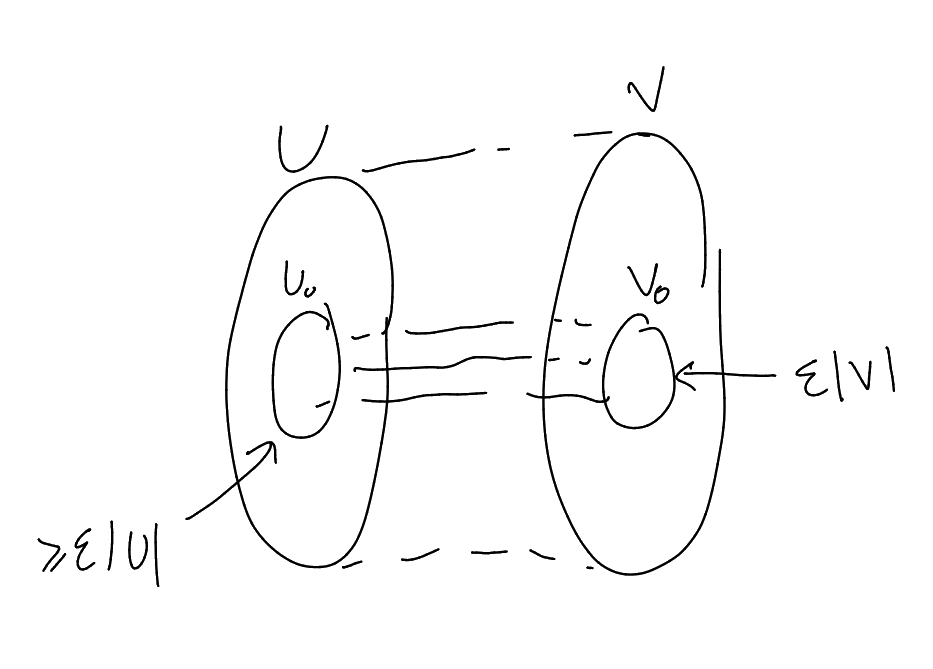
Definition 8.2 ( $e p s$ -uniform). We say that $(U, V)$ is $𝜀$ -uniform if $\forall U_{0} \subset U$ and $V_{0} \subset V$ ,

| d (U_{0}, V_{0}) - d (U, V) | \leq 𝜀

whenever $| U_{0} | \geq 𝜀 | U |$ and $| V_{0} | \geq 𝜀 | V |$ .

Fact: Let $G$ be a graph and let $U, V \subset V (G)$ disjoint which are $𝜀$ -uniform. Let $p = d (U, V)$ . Then

\begin{array}{l} | {x \in U : | N (x) \cap V | > (p + 𝜀) | V |} | & \leq 𝜀 | U | \\ | {x \in U : | N (x) \cap V | < (p + 𝜀) | V |} | & \leq 𝜀 | U | \end{array}

Proof. Simply note that if

S = {x \in U : | N (x) \cap V | > (p + 𝜀) | V |},

we have $d (S, V) > (p + 𝜀)$ , hence $| S | < 𝜀 | U |$ due to uniformity.

Second case is the same. □

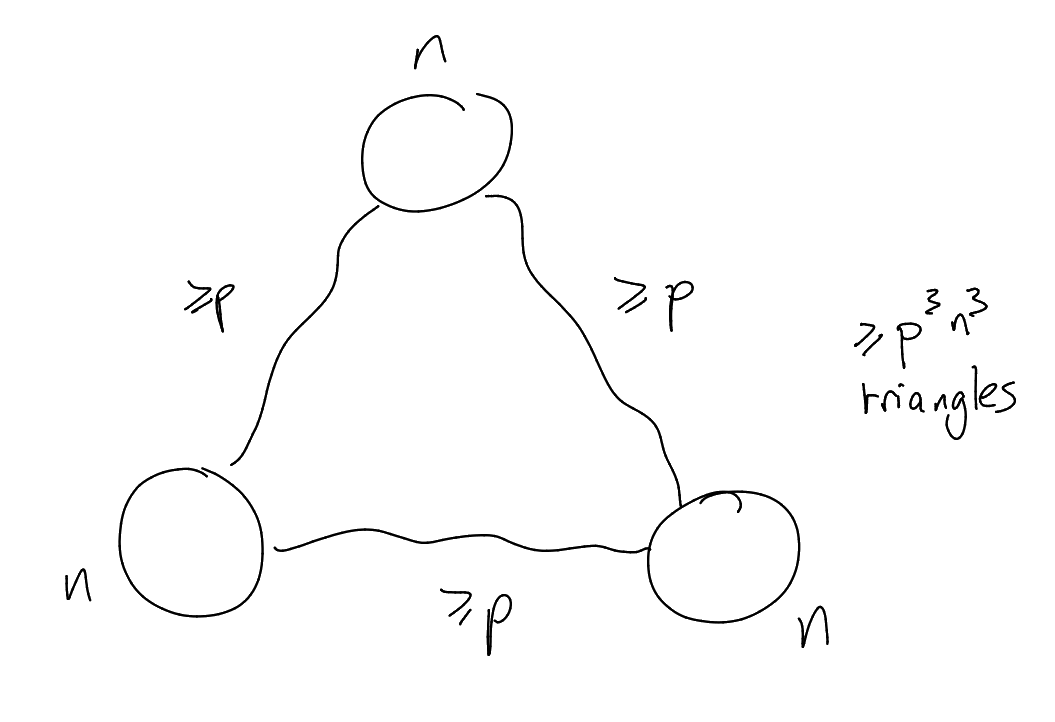
Lemma 8.3 (Counting lemma for triangles). Assuming that:

$G$ a graph on vertex set $V_{1} \cup V_{2} \cup V_{3}$ with $V_{i}$ disjoint
$| V_{i} | = n$
$𝜀 < \frac{p}{2}$
$d (V_{i}, V_{j}) \geq p$ and $(V_{i}, V_{j})$ is $𝜀$ -uniform

Then the number of triangles in

G

\geq (1 - 2 𝜀) {(p - 𝜀)}^{3} n^{3} .

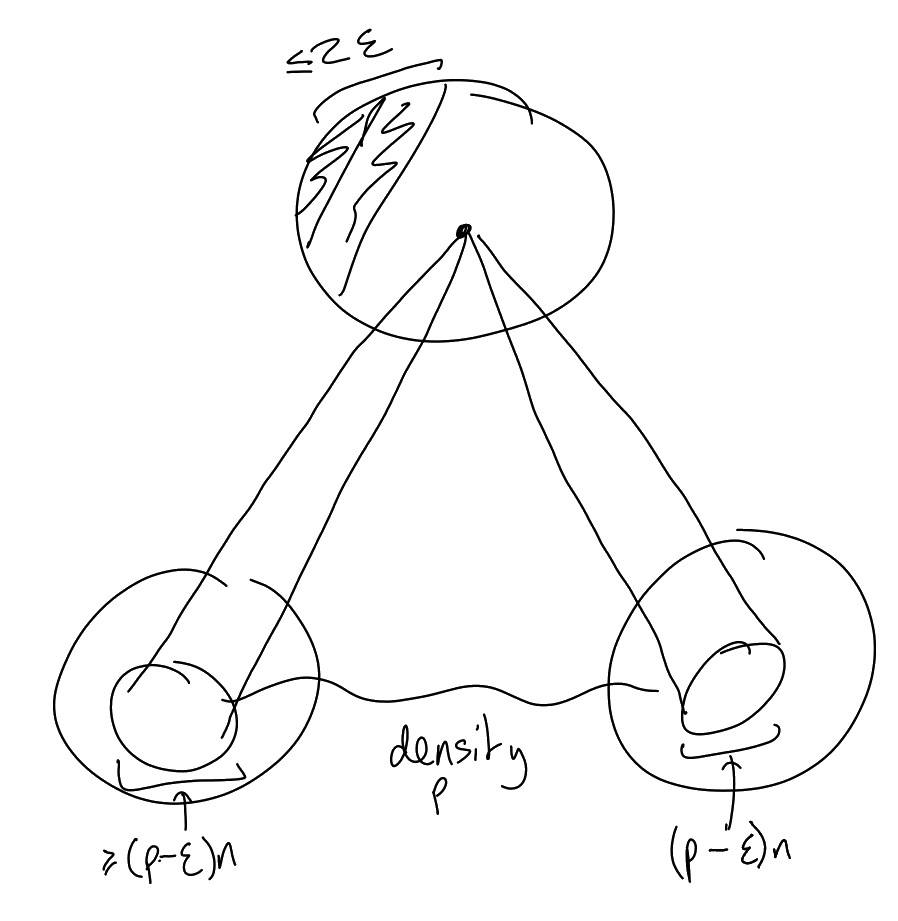
Proof. Let

V^{'} = {x \in V_{1} : | N (x) \cap V_{2} |, | N (x) \cap V_{3} | \geq (p - 𝜀) n} .

Note that $| V^{'} | \geq (1 - 2 𝜀) n$ . Now fix $x \in V$ and note

\begin{array}{l} e (N (x) \cap V_{2}, N (x) \cap V_{3}) & \geq (p - 𝜀) | N (x) \cap V_{2} | | N (x) \cap V_{3} | \\ \geq (p - 𝜀) (p - 𝜀) (p - 𝜀) n^{2} \end{array}

using the $𝜀$ -uniform and $p \geq 2 𝜀$ . So summing over all $x \in V^{'}$ gives us

(1 - 2 𝜀) {(p - 𝜀)}^{3} n^{3}

triangles. □

Definition 8.4 (Equipartition). Say that $V (G) = V_{1} \cup \dots \cup V_{k}$ is an equipartition if $| | V_{i} | - | V_{j} | | \leq 1$ for all $i, j$ .

Theorem 8.5 (Szemerédi Regularity Lemma). Assuming that:

$𝜀 > 0$ , $l \in ℕ$

Then there exists

L = L (𝜀, l)

such that the following holds: Let

G

be a graph. Then there is an equipartition of

V (G) = V_{1} \cup \dots \cup V_{k}

, where

l \leq k \leq L (l, 𝜀)

and such that all but

𝜀 (\binom{k}{2})

pairs

1 \leq i < j \leq k

, we have that

(V_{i}, V_{j})

𝜀

-uniform.

Remark.

Technically, the Szemerédi Regularity Lemma also applies when $e (G) = o (n^{2})$ , but often it does not really tell us anything.
The dependence on $𝜀$ of $L (𝜀)$ is of tower type, i.e.
$L (𝜀) \leq \underset{⏟}{munder} 𝜀^{- C} .$

Gowers proved that
$L (𝜀) \geq \underset{⏟}{munder} 𝜀^{c} .$

So these tower bounds are necessary.

Theorem 8.6 (The triangle Removal Lemma). For all $𝜀 > 0$ , there exists $δ > 0$ so that the following holds: Every graph $G$ on $n$ vertices with $\leq δ n^{3}$ triangles contains $T \subset E (G)$ with $| T | \leq 𝜀 n^{2}$ and $G - T ⁄ \supset K_{3}$ .

Proof. Let $𝜀 > 0$ be given, let $L = L (\frac{10}{𝜀}, \frac{𝜀}{4})$ and define $δ = \frac{𝜀^{3}}{16 L^{3}}$ . Let $G$ be a graph with $\leq δ n^{3}$ triangles.

Apply Szemerédi Regularity Lemma to $G$ to find $V (G) = V_{1} \cup \dots \cup V_{k}$ , with $k \leq L (\frac{10}{𝜀}, \frac{𝜀}{4})$ . Now define

\begin{array}{l} T & = {all edges between V_{i}, V_{j} whenever d (V_{i}, V_{j}) < \frac{𝜀}{2}} \\ \cup {all edges between V_{i}, V_{j} such that (V_{i}, V_{j}) not \frac{𝜀}{4} -uniform} \\ \cup {all edges inside of the parts V_{i}} \end{array}

We note

\begin{array}{l} | T | & \leq (\binom{k}{2}) \cdot \frac{𝜀}{2} {(\frac{n}{k})}^{2} + \frac{𝜀}{4} (\binom{k}{2}) {(\frac{n}{k})}^{2} + (\binom{\frac{n}{k}}{2}) k \\ \leq (\frac{𝜀}{2}) \frac{k^{2}}{2} {(\frac{n}{k})}^{2} + \frac{𝜀}{8} n^{2} + \frac{n^{2}}{2 k} \\ \leq 𝜀 n^{2} \end{array}

Let’s see that $G - T$ is triangle-free. If not, then $x, y, z \in V (G)$ with $x \in V_{i}$ , $y \in V_{j}$ , $z \in V_{r}$ . So we must have $d (V_{i}, V_{j}) \geq \frac{𝜀}{2}$ and $(V_{i}, V_{j})$ is $\frac{𝜀}{4}$ -uniform.

So we can apply the “counting lemma” for triangles to find that the number of triangles is at least

(1 - 2 𝜀) 𝜀^{3} {(\frac{n}{k})}^{3} \geq (\frac{1}{2} \frac{𝜀^{2}}{L^{3}}) n^{3} > δ n^{3},

which contradicts the initial assumption. □

Remark.

This proof gives tower-type dependence
$δ = mfrac$

between $δ$ and $𝜀$ .
It’s a big question to improve these bounds.
Best known is due to Fox, who proved that
$δ < mfrac$

is sufficient.

Theorem 8.7 (Roth). For $𝜀 > 0$ there exists $n (𝜀) \in ℕ$ such that if $n \geq n (𝜀)$ and $A \subset [n]$ with $| A | \geq 𝜀 n$ , then $A$ contains $a, a + d, a + 2 d$ where $d \neq 0$ .

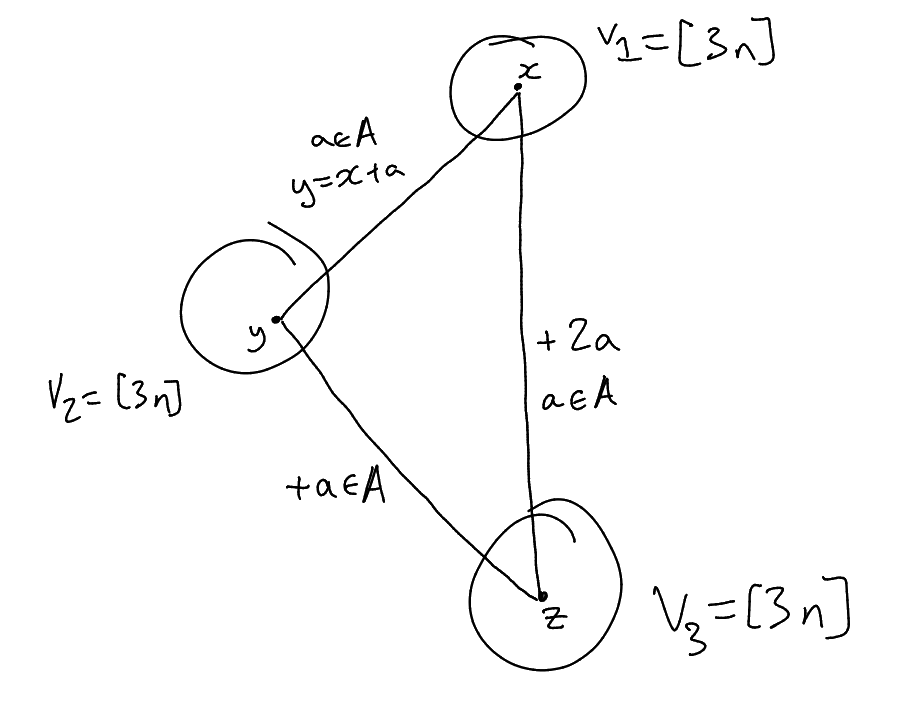
Proof. For $𝜀 > 0$ given, let $δ = δ (𝜀)$ be the $δ$ from The triangle Removal Lemma. Let $n (𝜀) \geq \frac{1}{δ (𝜀)}$ . Now given a set $A \subset [n]$ , we define a graph $G$ on $V_{1} \cup V_{2} \cup V_{3}$ where $V_{i}$ are disjoint copies of $[3 n]$ and:

\begin{array}{l} E (V_{1}, V_{2}) & = {{x, x + a} : x \in V_{1}, x + a \in V_{2}, a \in A} \\ E (V_{2}, V_{3}) & = {{y, y + a} : y \in V_{2}, y + a \in V_{3}, a \in A} \\ E (V_{1}, V_{3}) & = {{x, x + 2 a} : x \in V_{1}, x + 3 a \in V_{3}, a \in A} \end{array}

Say then $x \in V_{1}$ , $y \in V_{2}$ , $z \in V_{3}$ form a triangle in $G$ . So $y = x + a$ , $z = y + b$ , $z = x + 2 c$ for some $a, b, c \in A$ . Then

y + z + (x + 2 c) = (x + a) + (y + b) + z,

hence $a + b = 2 c$ . If $A$ is no $3$ -term arithmetic progressions, then $G$ only contains triangles of the form ${x, x + a, x + 2 a}$ , where $a \in A$ . So $G$ contains $\leq 3 n | A | \leq 3 n^{2}$ triangles.

So apply the The triangle Removal Lemma to find $T \subset E (G)$ with $| T | \leq 𝜀 n^{2}$ such that $G - T$ is triangle-free. This is possible since $n > \frac{10}{δ}$ . But now notice that

{{x, x + a, x + 2 a} : x \in [n], a \in A}

is a set of edge-disjoint triangles of size $n | A |$ and hence

n | A | \leq | T | \leq 𝜀 n^{2},

so $| A | \leq 𝜀 n$ . □

Remark.

Again this gives bad bounds on our minimum density $𝜀$ .
Roth showed that if $A \subset [n]$ , $| A | \geq c \frac{n}{\log \log n}$ , then $A$ contains a $3$ -term arithmetic progression.
Kelley–Meka showed that the same holds for $| A | \geq n e^{- c {(\log n)}^{\frac{1}{12}}}$ .

There exist $A \subset [n]$ with no $3$ -term arithmetic progression but
$| A | \geq n e^{- c \sqrt{\log n}} .$