1 The Ramsey Numbers
The course is Probabilistic Combinatorics, being lectured by
|
|
We will be studying in particular the Ramsey numbers. Starting with the simplest to define:
|
|
Example.
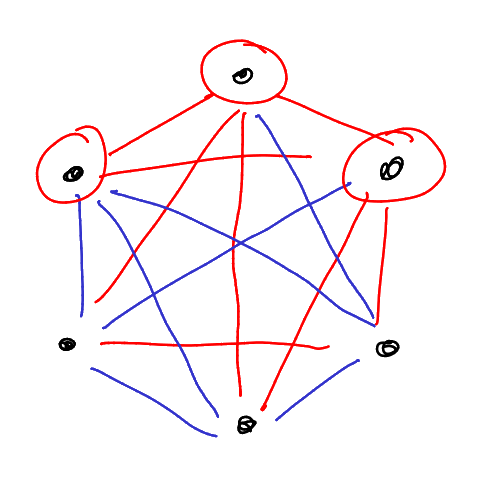
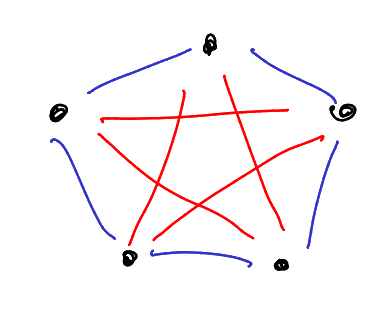
Thus
Main question: how fast does
We will also study:
|
|
For a fixed graph
|
|
Example.
For
|
|
Example. Mantel’s Theorem says that
|
|
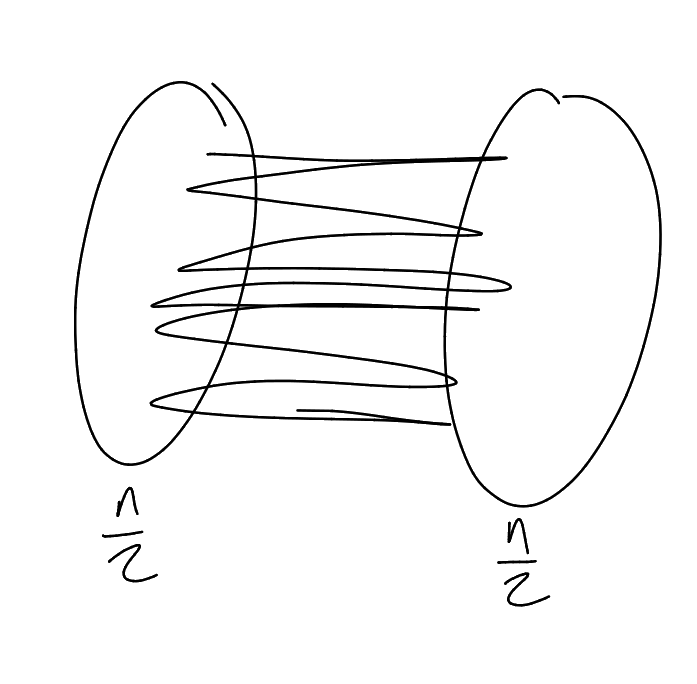
1.1 Binomial Random Graph
1.2 Topics in this course
-
First examples: “first moment method”.
-
-
deletion method
-
Lovász local lemma
-
Semi-random method
-
Hard core model
-
The triangle free process
-
-
Dependent random choice:
-
Ramsey numbers
-
Sidorenko conjecture
-
Extremal numbers of bipartite graphs
-
-
Pseudo-randomness
-
-
size-ramsey numbers
-
-
-
Szemeredi-Regularity lemma
-
Roth’s Theorem on 3-term arithmetic progressions in dense sets
-
Ramsey-Turán
-
-
Method of graph containers:
-
Counting graphs with no
-
-
-
1.3 Brief introduction to
Proof sketch.
Let
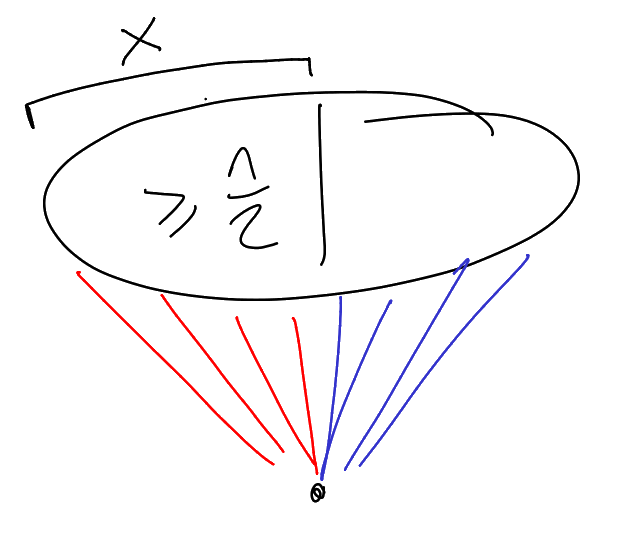
Now ignore everything that was connected using the other colour. Pick a new vertex from what remains, and apply the process again:
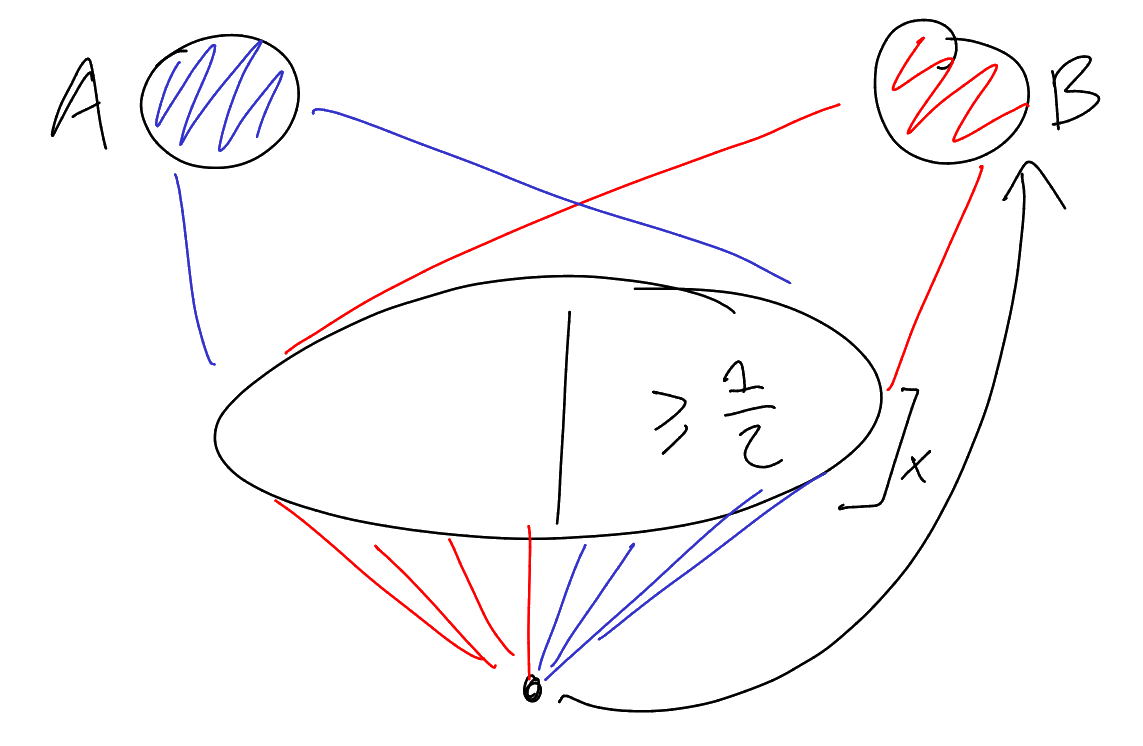
We continue until either
|
|
i.e.
How about a lower bound?
Example.
The following gives

Notation.
Proof.
Let
by the choice of
Big question: Is there an “explicit” construction that gives