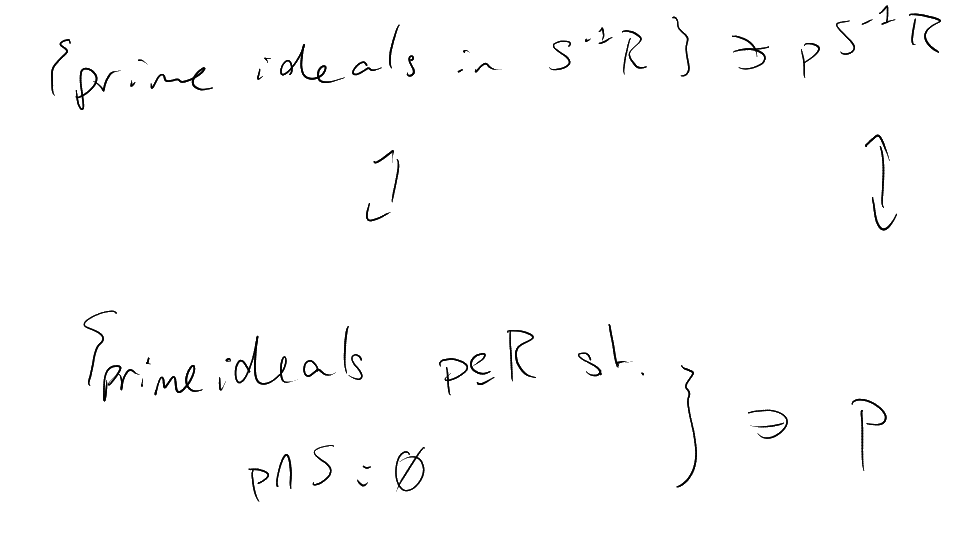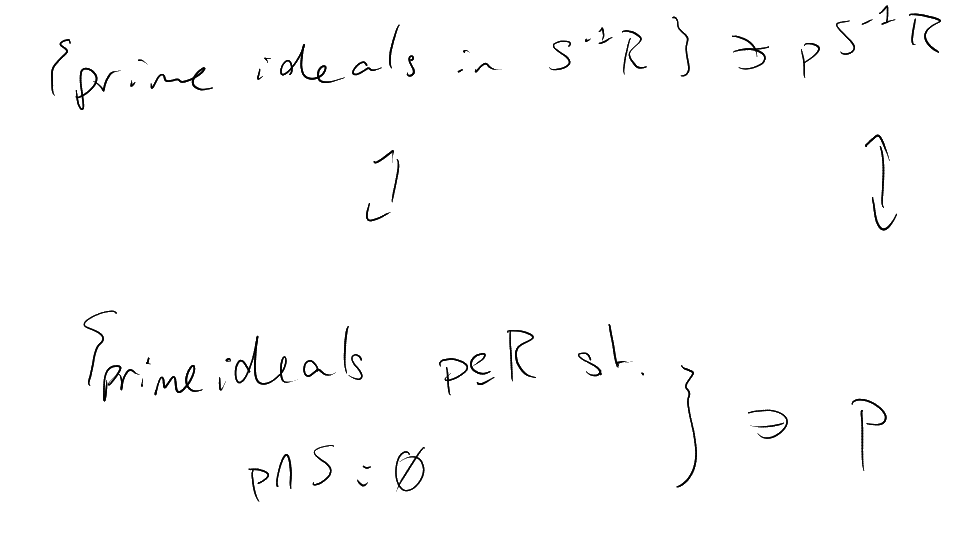Proof. Suppose not. Since $R$ is Noetherian, we may choose $I$ maximal with this property. Then $I$ is not prime, so there exists $x,y\in R\setminus I$ such that $x,y\in I$.

Let $I_1+(x)$, $I_2=I+(y)$. Then by maximality of $I$, there exist $p_1,\dots ,p_r$ and $q_1,\dots ,q_s$ such that $p_1\cdots p_r\subseteq I_1$ and $q_1\cdots q_s\subseteq I_2$. Then $p_1\cdots p_r{q}_1\cdots q_s\subseteq I_1{I}_2\subset I$. □

Proof. Let $I=(c_1,\dots ,c_n)$. We write

for some $a_{ij}\in R$. Let $A$ be the matrix $A={(a_{ij})}_{1\le i,j\le n}$ and set $B=x{\mathrm{id}}_n-A\in M_{n\times n}(K)$.

Then in $K^n$

Multiply by $\mathrm{adj}(B)$, the adjugate matrix for $B$. We have

Hence $\det (B)=0$. But $\det B$ is a monic polynomial with coefficients in $R$. Then $x$ is integral over $R$, hence $x\in R$. □

Proof of Theorem 9.2.

• $\Rightarrow$ Clear.
• $\Leftarrow$ We need to show $R$ is a PID. The assumption implies that $R$ is a local ring with unique maximal ideal $m$.

  Step 1: $m$ is principal.

  Let $0\ne x\in m$. By Lemma 9.3, $(x)\supseteq m^n$ for some $n\ge 1$. Let $n$ minimal such that $(x)\supset m^n$, then we may choose $y\in m^{n-1}\setminus (x)$.

  Set $\pi =\frac{x}{y}$. Then we have $ym\subseteq m^n\subseteq (x)$ and hence ${\pi }^{-1}m\subseteq R$. If ${\pi }^{-1}m\subseteq m$, then ${\pi }^{-1}\in R$ by Lemma 9.4 and $y\in (x)$, contradiction. Hence ${\pi }^{-1}m=R$, so $m=\pi R$ is principal.

  Step 2: $R$ is a PID.

  Let $I\subseteq R$ be a non-zero ideal. Consider a sequence of fractional ideals $I\subseteq {\pi }^{-1}I\subseteq {\pi }^{-2}I\subseteq \cdots$ in $K$. Then since ${\pi }^{-1}\notin R$, we have ${\pi }^{-k}I\ne {\pi }^{-(k+1)}I$ for all $k$ by Lemma 9.4. Therefore since $R$ is Noetherian, we may choose $n$ maximal such that ${\pi }^{-n}I\subseteq R$. If ${\pi }^{-n}I\subseteq m=(\pi )$, then ${\pi }^{-(n+1)}\subseteq R$. So we must have ${\pi }^{-n}I=R$, and hence $I=({\pi }^n)$. □

Proof. By properties of localisation, $R_{(p)}$ is a Noetherian integral domain with a unique non-zero prime ideal $p{R}_{(p)}$.

It suffices to show $R_{(p)}$ is integrally closed in $\mathrm{Frac}(R_{(p)})=\mathrm{Frac}(R)$ (since then $R_{(p)}$ is a Dedekind domain hence by Theorem 9.2, $R_{(p)}$ is a discrete valuation ring).

Let $x\in \mathrm{Frac}(R)$ be integral over $R_{(p)}$. Multiplying by denominators of a monic polynomial satisfied by $x$, we obtain

with $a_i\in R$, $s\in S=R\setminus p$. Multiply by $s^{n-1}$. Then $xs$ is integral over $R$, so $xs\in R$. Hence $x\in R_{(p)}$. □

Proof (Sketch). We quote the following properties of localisation:

• (i) $I=J⟺I{R}_{(p)}=J{R}_{(p)}$ for all prime ideals $p$.
• (ii) If $R$ a Dedekind domain, $p_1,p_2$ non-zero ideals, then

  $$p_1{R}_{(p_2)}=\{\begin{array}{cc}{p}_2{R}_{(p_2)}\hfill & p_1=p_2\hfill \\ R_{(p_2)}\hfill & p_1\ne p_2\hfill \end{array}$$

Let $I\subseteq R$ be a non-zero ideal. By Lemma 9.3, there are distinct prime ideals $p_1,\dots ,p_r$ such that $p_1^{{\beta }_1}\cdots p_r^{{\beta }_r}\subseteq I$, where ${\beta }_i>0$.

Let $0\ne p$ be a prime ideal, $p\notin \{p_1,\dots ,p_r\}$. Then property (ii) gives that $p_i{R}_{(p)}=R_{(p)}$, and hence $I{R}_{(p)}=R_{(p)}$.

Corollary 9.5 gives $I{R}_{(p_{)}}={(p_i{R}_{(p_i)})}^{{\alpha }_i}=p_i^{{\alpha }_i}{R}_{(p_i)}$ for some $0\le {\alpha }_i\le {\beta }_i$. Thus $I=p_1^{{\alpha }_1}\cdots p_r^{{\alpha }_r}$ by property (i).

For uniqueness, if $I=p_1^{{\alpha }_1}\cdots p_r^{{\alpha }_r}=p_1^{{\gamma }_1}\cdots p_r^{{\gamma }_r}$ then $p_i^{{\alpha }_i}{R}_{(p_i)}=p_i^{{\gamma }_i}{R}_{(p_i)}$ hence $a_i={\gamma }_i$ by unique factorisation in discrete valuation rings. □