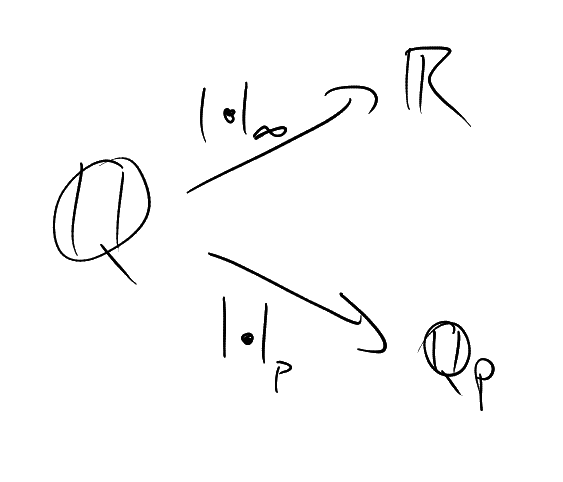
Example.
|
|
Although this is technically an absolute value, it is not useful or interesting, so should be ignored.
Verification:
|
|
|
|
An absolute value
Definition 1.3 (Place).
Let
Proof.
|
|
Assume that
|
|
Choose
|
|
Then we have
Hence
|
|
Remark.
|
|
for some fixed
Definition 1.5 (Non-archimedean).
An absolute value
|
|
If
Example.
Proof.
|
|
and
|
|
Proof.
For
|
|
The “In particular” is clear. □
Example.
Take
We choose
Analogy with

Notation. As is usual when working with metric spaces, we will be using the notation:
Proof.
Thus