Fermat’s Method of Infinite Descent - Elliptic Curves

Lemma 1.1. Assuming that:

$Δ$ is a primitive triangle

Then

Δ

is of the form

for some integers $u > v > 0$ .

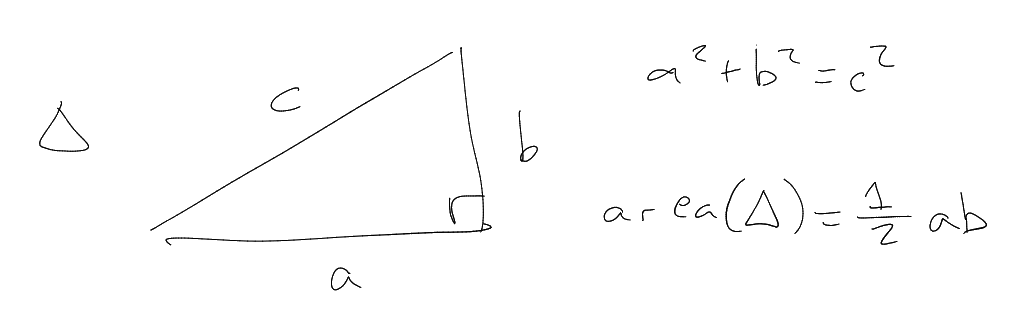
Proof. Without loss of generality $a$ odd, $b$ even (work modulo $4$ ). This then forces $c$ odd.

Then

{(\frac{b}{2})}^{2} = \frac{c + a}{2} \cdot \frac{c - a}{2},

and note that all the fractions are integers. Also note that the product on the right hand side is a product of positive coprime integers.

Unique prime factorisation in $ℤ$ gives that $\frac{c + a}{2} = u^{2}$ , $\frac{c - a}{2} = v^{2}$ for some $u, v \in ℤ$ .

Then $a = u^{2} - v^{2}$ , $b = 2 u v$ , $c = u^{2} + v^{2}$ . □

Lemma 1.2. Assuming that:

$D \in ℚ_{> 0}$

Then

D

is congruent if and only if

D y^{2} = x^{3} - x

for some

x, y \in ℚ

y \neq 0

Proof. Lemma 1.1 shows

D congruent ⟺ D w^{2} = u v (u^{2} - v^{2})

for some $u, v, w \in ℚ$ , with $w \neq 0$ . Put $x = \frac{u}{v}$ and $y = \frac{w}{v^{2}}$ . □

Proof. Without loss of generality $u, v$ are coprime, $u > 0$ , $w > 0$ . If $v < 0$ then replace $(u, v, w)$ by $(- v, u, w)$ . If $u, v$ both odd then replace $(u, v, w)$ by $(\frac{u + v}{2}, \frac{u - v}{2}, \frac{w}{2})$ .

Then $u, v, u + v, u - v$ are pairwise coprime positive integers with product a square.

Unique factorisation in $ℤ$ gives

u = a^{2}, v = b^{2}, u + v = c^{2}, u - v = d^{2}

for some $a, b, c, d \in ℤ_{> 0}$ .

Since $u ⁄ \equiv v (m o d 2)$ , both $c$ and $d$ are odd.

Then consider:

{(\frac{c + d}{2})}^{2} + {(\frac{c - d}{2})}^{2} = \frac{c^{2} + d^{2}}{2} = u = a^{2} .

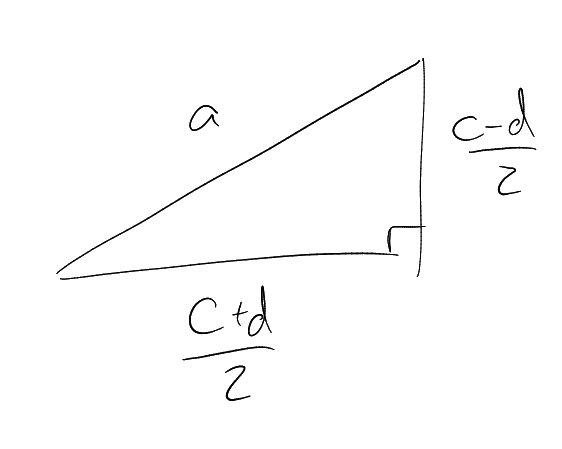
This is a primitive triangle. The area is $\frac{c^{2} - d^{2}}{8} = \frac{v}{4} = {(\frac{b}{2})}^{2}$ .

Let $w_{1} = \frac{b}{2}$ . Lemma 1.1 gives $w_{1}^{2} = u_{1} v_{1} (u_{1} + v_{1}) (u_{1} - v_{1})$ for $u_{1}, v_{1} \in ℤ$ . Therefore we have a new solution to ( $*$ ). But $4 w_{1}^{2} = b^{2} = v | w^{2}$ so $w_{1} \leq \frac{1}{2} w$ .

So by Fermat’s method of infinite descent, there is no solution to ( $*$ ) . □

1.1 A variant for polynomials

Lemma 1.4. Assuming that:

$u, v \in K [t]$ coprime
$α u + β v$ is a square for $4$ distinct $(α : β) \in ℙ^{1}$

Then

u, v \in K

Proof. Without loss of generality $K = \bar{K}$ .

Changing coordinates on $ℙ^{1}$ , we may assume the ratios $(α : β)$ are $(1 : 0), (0 : 1), (1 : - 1), (1 : - λ)$ for some $λ \in K ∖ {0, 1}$ (Möbius map).

\begin{array}{l} u & = a^{2} \\ v & = b^{2} \\ u - v & = (a + b) (a - b) \\ u - λ v & = (a + μ b) (a - μ b) \end{array}

(where $μ$ is a square root of $λ$ ). Unique factorisation in $K [t]$ gives that $a + b$ , $a - b$ , $a + μ b$ , $a - μ b$ are squares. But

\max (\deg (a), \deg (b)) \leq \frac{1}{2} \max (\deg (u), \deg (v)) .

So Fermat’s method of infinite descent, we get a contradiction, unless the degrees of $u$ and $v$ are zero. So $u, v \in K$ . □

Definition 1.5 (Elliptic curve (temporary definition)).

(i) An elliptive curve $E ∕ K$ is the projective closure of the plane affine curve
$y^{2} = f (x)$

where $f \in K [x]$ is a monic cubic polynomial with distinct roots in $\bar{K}$ . We call this equation “a Weierstrass equation”.
(ii) For $L ∕ K$ any field extension
$E (L) = {(x, y) \in L^{2} | y^{2} = f (x)} \cup {0} .$

$0$ is the “point at infinity” that we get because we take the projective closure.

In this course, we study

E (K)

for

K

being a finite field, local field (

[K : ℚ_{p}] < \infty

) or number field (

[K : ℚ] < \infty

Proof. Without loss of generality $K = \bar{K}$ . By a change of coordinates, we may assume

y^{2} = x (x - 1) (x - λ)

for some $λ \in K ∖ {0, 1}$ . Suppose $(x, y) \in E (K (t))$ . Put $x = \frac{u}{v}$ , where $u, v \in K [t]$ are coprime.

Then $w^{2} = u v (u - v) (u - λ v)$ for some $w \in K [t]$ .

Unique factorisation in $K [t]$ gives that $u, v, u - v, u - λ v$ are squares. Hence by Section 1.1, $u, v \in K$ , so $x \in K$ , so $y \in K$ . □

1 Fermat’s Method of Infinite Descent

1.1 A variant for polynomials