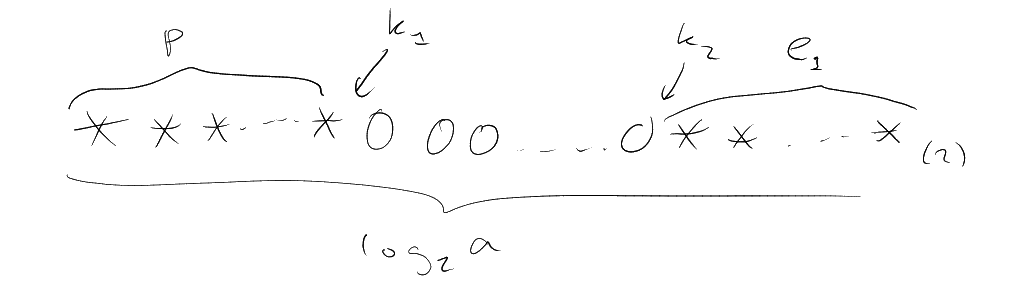1 Diophantine Approximation
Theorem 1.1 (Dirichlet).
Assuming that:
Then there exist infinitely many
such that
Proof.
Consider the numbers
for some fixed .
Consider them in .
Note
|
|
By the box principle (pigeonhole principle), there exists
such
that
and
belong to the same interval. Then:
for some .
Take .
Then
Take ,
then you get an infinite sequence of rationals. If
is not raitonal, then this sequence cannot stabilise, so we get infinitely many
as desired. □
Can we do better?
In particular for .
Theorem (Liouville).
Assuming:
Then there exists
such that for all
with ,
we have
Proof.
Let be the
minimal polynomial of ,
so . Now note that
(by irreducibility
when , and for
using the
hypothesis that ).
Then
Note that is rational
with denominator .
On the other hand,
|
|
provided ,
which we may assume. Hence
□
Improvements of the exponent
in Liouville:
Theorem 1.2 (Roth).
Assuming that:
Then there exists
such that for all
we have
Theorem 1.3 (Thue).
Assuming that:
Then the equation
has only finitely many solutions in
with .
Liouville’s theorem
.
Lemma 1.4.
Assuming that:
Then for all
,
there exists
root of
such that
|
|
Here ,
depend on
, and a fixed compact
set that contains .
Proof.
Let
with
distinct (since we assumed no repeated factors, and characteristic
fields are always separable). Without loss of generality assume that
is the closest to .
Then
for some constants depending on
and the compact set for .
So we get lower and upper bounds on .
□
Proof of Thue.
Suppose . The
lemma tells us that there exists
a root of
such that
|
|
If the degree of ,
then Roth or already Thue implies that
must be bounded, hence only finitely many solutions.
For ,
we use Liouville. □
Let .
The height of it is
|
|
Theorem 1.5 (Subspace theorem, Archimedean version, Schmidt).
Assuming that:
Then for all
the solutions of
|
|
for
are contained in a finite collection of proper linear subspaces of
, which
depend only on .
The volume of the region is
|
|
is .
Consider the paralellepipeds:
for some
with .
This implies Roth’s theorem:
Let
irrational. Consider the linear forms
Let . Then
()
is equivalent
to . If
, then this is equivalent
to . Roth’s theorem is
true apart from
contained in a finite collection of subspaces. A subspace is of the form
for
some or
maybe .
Obvious subspaces:
-
-
Example :
,
,
. Consider the
subspace .
Now ()
becomes:
or alternatively
|
|
This has plenty of solutions by Dirichlet if .
-
A line, that is a -dimensional
subspace may contain only finitely many solution.
The places of is
and it consists of all
prime numbers and .
For each , we define
an absolute value on .
is the ordinary absolute
value. If is a prime
number, this is the -adic
absolute value, that is, for ,
where
is maximal
such that .
For , we
define .
If , then:
-
-
When ,
This is called the ultrametric inequality.
Theorem 1.6 (Subspace theorem, -adic version with Q coeffs).
Assuming that:
-
-
with
-
for each ,
let
be linearly independent forms with rational coefficients in
variables
Then the solutions of
|
|
with are contained in a finite
collection of proper subspaces of .
,
,
,
,
. Consider
. Let
with
not
divisible by 2 or 3.
|
|
Consider ,
, then
|
|
What happens if you replace
with ?
Proposition 1.7.
Assuming that:
Then there exists
such that for
,
we have
|
|
or .
Proof.
Take ,
. Let
for all
, except:
. Then
the solutions of
|
|
with
are contained in the lines: ,
,
plus finitely many points.
Plug in ,
. Then
|
|
provided does not
satisfy the claim with .
Also,
|
|
|
|
so
|
|
Assume
by symmetry. Then
We can assumme that , for
otherwise the claim is trivial. Then .
Then
Then either
or
is one of finitely many exceptions.
Make
small enough to rule out the exceptions. □
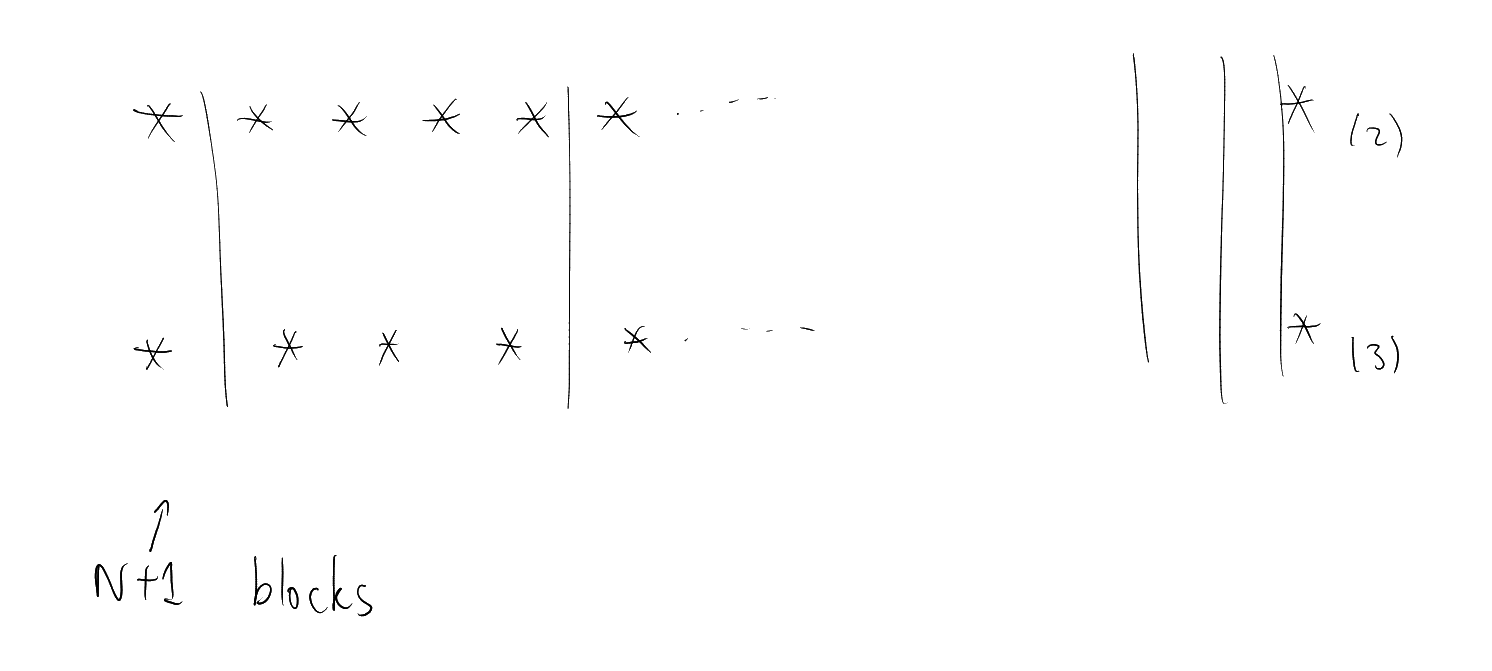
For , let
denote the number of
non-zero digits in the base
expansion of .
Theorem 1.8 (Senge, Strauss).
We have
as .
Despite the fact that this statement looks quite modest, the proof is not so simple.
Proof.
Take :
we assume that
for some fixed .
Consider its base
expansion.
First we will explore the consequences of having a large string of
s in the
base
expansion.
Then .
We know:
|
|
Similarly:
with
and .
We will make sure that .
|
|
Want to use the proposition. So we need:
|
|
So we want
|
|
We want
|
|
Since at most
blocks have a non-zero number, one of the blocks only has zeroes, which can be used with the above to show
that
cannot be too large. □
The constants in all results so far (except Liouville) are ineffective!
Are there any improvements of
(suppose is the best you
can get with Liouville) for .
No!
To demonstrate what it means that the above results are ineffective:
Suppose that we want to find all the solutions of .
Thue says that we have finitely many. But because it is ineffective, we have no idea how to bound the largest
of these is, so would struggle to find all solutions, even with an arbitrarily powerful computer (or an army of
postdocs).
1.1 Transcendence
Liouville proved
is transcendental.
What about ,
,
?
Hermite: is
transcendental.
Lindemann: If , then
at least one of
or is
transcendental.
Theorem 1.9 (Lindemann-Weierstrass).
Assuming that:
Then are linearly
independent over
(algebraic closure of ).
Hilbert’s 7th problem: Let ,
algebraic, irrational
algebraic. Then
is transcendental.
Note (for this problem): where
is any complex number with
. So in the above problem we can
think of “ is transcendental”
as meaning “any choice for
is transcendental”.
Convention: If ,
then .
Theorem.
Let be non-zero
algebraic numbers. Then are linearly
independent over if and only if
they are linearly independent over .
Proof of Hilbert’s 7th above Theorem is true.
-
Suppose
are dependent over .
Then
such that .
Then
either
or .
-
Suppose there exists ,
non-zero algebraic such that
for some .
Then
for some choice of the logarithms. If the logarithms are ,
then we deduce ,
a contradiction. Otherwise, we deduce that
(by the above theorem), which is also a contradiction. □
Theorem (Baber).
Let
be -linearly
independent logarithms of algebraic numbers.
Then are linearly
independent over .
Conjecture 1.10 (Schanuel).
Let
be linearly independent over .
Then the transcendence degree of
is at least .
Let , and
. Let
be the max of the numerator
and the denominator of .
Let .
Then
|
|
|
|
|
|
Notation.
Let ,
denote its minimal polynomial in
by .
If , then
(the height
of ) is
the maximal absolute value of its coefficients.
Theorem.
Let ,
.
Fix some choices of .
Let .
Let . Then there exists
an effective constant
depending on
and the degree of
such that either
or
|
|
Conjecturially: this should be
|
|
Theorem.
Let . Let
be a choice of their
logarithms. Let .
Let
Then there is an effective constant
that depends only on
and the degree of
such that
|
|
Observe
|
|
Recall
|
|
Typical scenario:
fixed numbers, ,
.
In the setting of Diophantine approximations, it is possible to show
with
and
being effective constants.
Proposition.
There is an effective absolute constant
such that
for all :
|
|
or .
Proof.
Suppose .
|
|
,
Then:
|
|
|
|
Multiply by .
□
Before:
|
|
The new bound wins when .
In particular, when :
|
|
for
,
.
Recall: is the number of
non-zero digits in the base
expansion of .
Theorem (Stewart).
There is an effective absolute constant
such
that
|
|
for .
Digit expansion of
.
We need where
(this is an upper bound
for the exponent of in the
proposition). Previously we have .
Alternative to heights of minimal polynomials (is better behaved under operations like addition):
Definition 1.11 (Mahler measure).
Let
Then we define
|
|
We could define the height of an algebraic number
as
but instead we will define it in a different (but equivalent) way.
Consider two algebraic integers ,
and assume
|
|
This means that the Galois-conjugates are
where runs through
the conjugates of
and runs through
the conjugates of .
Then
Recall that we mentioned that we could define
Then would have
Similarly,
Proposition.
Let
of degree .
Then
Proof.
For the upper bound:
|
|
Known as Jensen’s formula (enough to prove for
of degree ).
Note that
for all .
This with Jensen’s formula gives the upper bound. For the lower bound:
Then
|
|
The number of terms is .
Hence .
□
Absolute Values
Let be a number
field. Then a function
is an absolute value if:
Example.
-
Trivial absolute value:
for all .
-
Let
be an embedding. Then .
-
Let
be a non-zero prime ideal lying above .
(This means ).
Then we define
on
as follows: for ,
is the largest
such that .
For ,
.
Let
(ramification index). Then we define
Comment on the normalisation: for ,
we have ,
and .
The places of
are
comprises:
-
all embeddings
such that
-
one from each complex conjugate pairs from the rest
-
all (non-zero) prime ideals
For ,
denotes
the absolute value given above.
Infinite places: :
embeddings.
Finite places: :
prime ideals.
For , we
define
as follows:
-
if
is a real embedding, then .
-
if
is complex, then .
-
if
is a prime ideal, then ,
where:
(where
is the rational prime below ).
Comment:
where is
the place of
below .
extension of
number fields, then
lies above ;
in notation .
If both are embeddings and
or or both are
finite and lies
over as prime
ideals, i.e. .
Remark.
,
.
Proposition (Product formula).
Let
be a number field. Then for all ,
we have
Proof.
We compute
in two ways.
|
|
where
is the rational prime lying below .
Recall .
So
Also,
|
|
Dividing the equations gives the desired result. □
Now we define
|
|
We will also use .
We won’t be using that much, but we mention it mostly because it is used in the literature.
is known as “multiplicative
height”, while
is known as “logarithmic / absolute / Weil height”.
Proposition 1.12.
Let be an
extension of number fields. Let .
Then as defined
above is the same for
and .
Proof.
Claim 1: If ,
such that
then
for all .
Claim 2: .
Assuming these claims are true, then for
|
|
Then
|
|
Which implies the desired result.
Proof of Claim 1: Will show if
are embeddings then
If are
prime ideals, then we need
For this, note that for all ideals ,
we have
|
|
Use this for
and in the
role of :
Proof of Claim 2: Omitted. □
Proposition.
Let .
Then
Remark.
Recall .
Proof.
Enough to prove
|
|
where
is a number field with .
If ,
then this is immediate from the definitions.
For a polynomial ,
we write
for the maximum
of all the coefficients of .
A variant of Gauss’s lemma can be stated as follows: Let .
Then
for .
Observe that
(for all )
because the coefficients are coprime rational integers. We write
(we take
to be the
splitting field of ).
Gauss’s lemma gives
|
|
Let be an
automorphism of
such that for
some fixed .
This permutes .
That is, ,
there exists
such that .
So
By the product formula:
|
|
So
|
|
Lemma.
Let ,
and .
Then
Proof.
If ,
then this is immediate from the definition. So just need to consider
:
|
|
(). We
multiply this by
So
|
|
□
Let
be a polynomial in possibly several variables, with complex coefficients. Then
is
defined to be the sum of the absolute values of all the coefficients. This is sometimes called the length of
.
Proposition.
Let ,
. Let
of
degree
in . Let
. Then:
|
|
In particular:
and .
Proof.
Let be a number
field containing all .
Let first .
Then
For :
|
|
So
|
|
Then taking a
root of both sides gives the desired inequality. □
Lemma.
Let .
Then:
|
|
This is sometimes known as “trivial bound” or “Liouville’s bound”.
Proof.
|
|
Apply this for :
□
Theorem (Siegel).
Let be a real
algebraic irrational number. Then for all ,
there exists
such that
for all .
We will spend the next 3-5 lectures proving this.
We will spend today’s lecture discussing an outline of the proof, discussing why certain parts are necessary
and also some intuition as to why one would expect this method to work.
-
(1)
Suppose to the contrary that there are infinitely many
such that .
-
(2)
Choose two among these appropriately, which I will denote .
-
(3)
Construct a polynomial
that vanishes at
to high order.
-
(4)
Give a lower bound on .
-
(5)
Give an upper bound on .
-
(6)
Realise that they give a contradiction.
1 variable is not enough: let
be of degree .
Then may
vanihs at to
order .
Then we have a lower bound of
and we might hope for an upper bound like
To get a contradiction, we need ,
i.e. .
Lower bound
where is the
degree in
and is the
degree in .
Upper bound:
|
|
where .
Note
|
|
Index of at
with respect to
the weights .
|
|
Use ,
. With
this, we get the upper bound
|
|
How big can be
made? We look for
in the form
|
|
The condition that is
a linear equation for
over .
By picking a basis of
over , this becomes
a system of linear
equations. To find
such that
we need to solve:
|
|
I can choose ,
and I want to do the following:
|
|
Take for
some large .
Subtleties that still need to be considered:
coefficient
of is
, where
is the
coefficient of
in .
.
Thue: .
Let be a
linear form in
where
is a number field.
For :
where
. Then
define
|
|
By the product formula, this is invariant under multiplication by an element
:
so
|
|
Lemma (Siegel’s lemma).
Let
be a number field of degree .
Let such
that and let
. Let
be linear forms
such that . Then
there exist
(not all )
such that
for and
In particular, if ,
then the bound is .
There is a refinement of this lemma which is due to Bombieri and Vaaler.
Corollary.
Let be an
algebraic number of degree .
Let ,
and let .
Let .
Suppose that
|
|
Then there exists
of degree in
such
that
and
where
is the maximal absolute value of hte coefficients.
Proof.
For
consider:
|
|
where are
variables of .
Then
|
|
where
|
|
Need to find
such that
for all
with .
Apply Siegel’s lemma:
|
|
Then
We need to estimate .
For finite places ,
|
|
For infinite places:
|
|
Then
|
|
Then Siegel’s lemma gives the bound
|
|
Proof of Siegel’s lemma for .
We can assume that the coefficients of each
are integers, and that they are relatively prime. Then each coefficient is bounded by .
Take .
Consider .
Evaluating
at all such
we have
|
|
The number of possible values of
is .
Claim: .
Indeed:
The claim follows by
Note that the above line uses the fact that !
By the box principle, there exist ,
with entries bounded by ,
such that
|
|
In the case, a key
step is that for
and , the points
are integers confined
in an interval of length
(where ).
In the general case, consider the map:
The -component
of is confined in an
interval (or box) of size .
Let . By
the product formula,
|
|
Make sure
RHS of above.
Non-vanishing:
Proposition.
For every ,
there exists such that
the following holds. Let ,
and let .
Suppose that
for ,
and that .
Let of
degree in in
for
such
that
for .
Then
|
|
Note: from now on, whenever we say ,
we also mean .
When we apply this we will have .
Without the asymmetry assumption (),
we have the counterexample: ,
with .
Alternatively: (for
some small degree
polynomials) for any
such that
Lemma.
Let ,
and let .
Let and
. Then
the following holds:
Baby case:
for some
polynomials.
In this case if
then either
or .
If vanishes
at to order
for
some ,
then
The leading coefficient of is
divisible by .
In particular, .
Then or
.
Hence ,
which contradicts the assumptions.
In general, we can always write
|
|
with .
Consider .
|
|
We will later have to worry about whether the resulting polynomial is
.
For any :
The degree increases -fold,
but not the index.
where ,
.
Lemma.
Let be
-linearly independent
polynomials in .
Then
|
|
(Wronskian)
Proof of Proposition assuming the lemma.
Suppose to the contrary that the proposition does not hold for some
. Write
such that
is minimal.
Then
and the
and are
-linearly
independent. Then consider
|
|
and
|
|
Then
by the above Lemma.
Note ,
,
.
Also
for .
.
Then
. If
,
. By the
indirect assumption
|
|
|
|
|
|
If vanishes
to order
at , then
divides the leading
coefficient of .
In particular, .
Then
|
|
|
|
If is sufficiently
large in terms of ,
then
|
|
A contradiction. □
Now we prove the lemma from earlier:
Lemma.
Let be
-linearly independent
polynomials in .
Then
|
|
(Wronskian)
Proof.
The statement does not change if we replace
by
for some
and
provided .
Then we may assume:
and the
are distinct.
We will prove that:
|
|
Then this is the leading term of th Wronskian, so this will prove the claim. The determinant is equal to:
|
|
Supose to the contrary that a non-trivial linear combination of the rows is .
Now the -th
row is a polynomial of degree evaluated
at .
Then the linear combination of the rows is a non-zero polynomial of degree
evaluated at .
□
Theorem.
Let be an irrational,
real algebraic number of degree .
Then for all ,
there exists
such that
for all .
Proof.
Suppose to the contrary that there are infinitely many
with
Then fix
sufficiently small in terms of
and let
be the constant when the proposition is applied with
in place of .
Now let
be such that
and
|
|
We use Siegel’s lemma to construct
that vanishes at
to high order.
We choose
such that
|
|
We want a polynomial
such that
|
|
For this we need to estimate
This is because
|
|
so
|
|
So we find
such that
and .
We need:
|
|
for and
. This will be fine
if . This is fine if
is sufficiently small
with respect to
and .
Then . Then there
exists a partial
derivative of
such that
|
|
if is
sufficiently small.
. Then
|
|
Taylor’s formula:
|
|
If are such
that ,
then
|
|
hence
The exponent is smaller than !
Now estimate the coefficients:
and
Contradiction. □
Theorem (Gelfond-Schneider).
Let
be logarithms of non-zero algebraic numbers. Then
are linearly independent
over if and only if they are
linearly independent over .
We will prove this by assuming ,
and then showing that a particular determinant is both equal to zero and not equal to zero, hence getting a
contradiction.
Before doing this, we will discuss how the previous proof could have been instead been phrased using
determinants.
We considered some functions which
were some enumeration of . Then
we used Siegel’s lemma to find
such that vanishes at
to some order. (Note
that also vanishes at all
Galois-conjugates of :
). Then we find an
argument to show that
also vanishes at
to some order.
This means that for there
exists and some partial
differentiation operator
such that . We
also showed that
with so much vanishing cannot exist.
Let:
|
|
Then
having all that vanishing is equivalent to
Now the existence of
is equivalent to .
Let ,
and ,
. Let
. So we
assumed that Gelfond-Schneider is false. We aim for a contradiction.
Let
with
|
|
Consider the “monomials”
for ,
and the
points
for .
Notation.
means a matrix
with rows indexed by
and columns indexed by .
Let
Steps:
-
(1)
Give an analytic upper bound on
-
(2)
Give an arithmetic lower bound on
-
(3)
“zero estimate” .
Steps (1) and (2) will be done in such a way that together they will give
. Then
this will contradict (3).
We will alternate between viewing as a
function of a single variable (function of )
and thinking of it as a function of two variables (function of
and
).
Upper bound
Proposition.
For ,
there exists
such that the following holds:
Let ,
. Let
be analytic functions (here, analytic means convergent power series on
). Let
. Let
. Then
|
|
Notation.
.
Corollary.
With as
above, there exists
depending only on ,
such that for all :
|
|
Proof.
We take
and some .
We have
with .
|
|
for ,
with .
□
One possible choice of the parameters: .
,
,
. In this
case:
(for large ).
Lemma (Schwart’s Lemma).
Let
be a holomorphic function on
the disc of radius
with a zero of order
at . Then:
for all :
Proof.
The maximum modulus principle for .
□
[Proof of Proposition.
] We apply Schwart’s Lemma for
and .
Note: .
So the proposition follows if we show that
vanishes to order
at .
We prove this. Enough to do it when each
is of the form
for some
depending on .
This is because all s
are infinite linear combinations of such s,
and hence the determinant can be written as an infinite combination of special determinants. Furthermore
we may assume that the
are distinct for different s.
Observe:
if each
is of the special form.
The number of monomials with degree
is at most .
We take .
Then at least half of the s
have degree .
So .
□
Proposition (1).
Let
be non-negative integers. Let
and
be two sets of distinct real numbers.
Then
|
|
with: ,
,
.
alternant / interpolation determinant
Proposition (2).
Let ,
let be distinct real
numbers. Let
be non-zero. Then the function
|
|
has at most
real zeroes counting multiplicities.
Proposition (2) Proposition (1).
Suppose to the contrary that .
Then there exists
not all
such that
vanishes for all .
This is a function of the type in Proposition (2). Each polynomil is of degree ,
and there are
many of them, so there can be no more than
zeroes. □
Lemma 1.13.
Let
be a function
on with
real zeroes.
Then has
at least
zeroes.
Corollary of Rolle’s Theorem.
Proof of Proposition (2).
By induction on .
If ,
then
and .
So
for some .
This indeed has no zeroes.
Suppose
and the claim holds for .
We assume as we may that
(if not, then replace
by ,
which has the effect of replacing
by ).
Then by the lemma,
has at most one more zero than
|
|
By the induction hypothesis,
has at most
zeroes, so
has at most
zeroes. □
Now we return to proving Gelfond-Schneider.
Let such
that for
.
We aim for a contradiction. We have integers
such that
Let
|
|
Last time:
|
|
where
arbitrary.
Apply Proposition (1) with
with some enumeration of
and .
Then .
Recall:
|
|
Then
for some .
So:
|
|
using
and
we get
Liouville bound:
|
|
Take: .
Then we have a contradiction if
|
|
I want:
Take: ,
,
.
Theorem (Nesterenko).
Let .
Let such
that ,
, and the exponentials of
the second coordinates of
and the first coordinates of
are distinct. Let
of degree in
, and
in
. Suppose that
vanishes on
. Then
Proof.
If ,
then
vanishes at exactly the same places as .
So we may assume .
Suppose that ,
and write .
Then
vanishes on
for all .
We write
with .
Then
|
|
Write
|
|
Then
|
|
I look for polynomials
such that
|
|
such that ,
and then since
vanishes at the first coordinates of ,
will follow. □
Lemma.
Let
for for some
. Then there
exists
such that
|
|
Proof.
Let be
the adjugate of .
Then
|
|
Let
be the first row of .
□
|
|
Premultiply this by the row vector .
We get ()
with .
.
We need to make sure that
The leading term of
is , where
is the leading
coefficient of .
To show , we will consider
the leading term of :
|
|
Lemma.
Let ,
wne let . Let
such that
. Then there
exists a choice of
such that
Proof.
By induction on .
is true.
Suppose , and the
claim holds for .
Consider the determinant:
|
|
which has the property that the upper left
minor is .
Now
is a polynomial which is
of degree ,
so it has at most
many s.
Choose
such that
is not one of them. □
Theorem.
Let . Let
be a homogeneous
polynomial of degree
without repeated factors. Let
be of degree .
Assume
is irreducible. Then
has at most finitely many solutions.
Schinzel proved this only assuming that
for some irreducible
of degree .
He used Siegel’s theorem on integral points. If an algebraic curve has infinitely many points, then it has genus
and at
most
points at infinity. Our proof is based on an argument of Corvaja and Zannier for proving Siegel’s
theorem.
Subspace theorem: Let be
a vector space of dimension
over .
Let and
be two bases of
. Then for all
, there exists a finite
number of elements
such that all
that solves:
|
|
with for
all ,
satisfies
for
some .
such
that
and .
satisfies
()
if and
only if
|
|
satisfies
|
|
Let be as in the
theorem, and write .
We assume that .
Then there exists
distinct such that
Write for
the set of
with . Then
for we
have
By a similar argument to the lemma for Thue’s equation, for all
there exists
such
that
with ,
then for
some .
We pick a small ,
in particular
for . We
define
for .
is bounded so only has finitely many integer points. We want to show this also for
. Write
for the ideal
generated by . Take
some and large
enough. Write for
polynomials of degree .
We will apply the subspace theorem in the vector space
|
|
Elements can be
evaluated on .
In particular, for ,
the map is an
element of . Reference
basis: the monomials
for span
. Pick a linearly
independent family for ,
where .
If , then
. Also,
|
|
We need to find some ’s
that decay on a fixed .
For we introduce a
symbol and call these
the “points of at
infinity”. We define for :
|
|
Note .
Lemma.
Let
and let .
If , then
the limit
|
|
exists and .
In addition, we have
|
|
for all .
Can be proved that
if and only if .
is a local
uniformiser at .
Proof.
Let ,
and by taking the substitution ,
we may assume .
First, we show
is bounded on .
To this end:
|
|
Note
on , with
some . We
may write
as:
(
of degree
in ).
is not the same as in the factorisation of
and ,
but
may be .
This gives:
|
|
For some polynomial .
Then
on .
Proving the first claim, suppose we can write
|
|
Here, negative exponents of
are allowed, but the sum must be finite. You can always do this with
if .
Then
and
and the claim holds.
If ,
then use ()
to write ()
with
replaced by .
Iterate this. □
Lemma.
For each ,
there is a basis
() of
such
that
Proof.
By induction, we show that there
and
such that
is
trivial: .
So suppose and the
claim holds for .
We define: to be
an element in of
minimal order at .
Let .
Just need to show: .
To this end, let .
Write .
Then
Then
so by the previous lemma, .
So .
□
For this to be useful, we need
to be large. (We need ).
Remark.
Thinking about
as a projective curve,
is the space of rational functions with poles of order at most
at each point
at . By
Riemann-Roch: ,
provided is
large enough.
Proof.
Let
(). The
point is that the polynomials
|
|
are linearly independent in .
,
.
Suppose
for some
not all .
Want to show .
To that end, let
such that
is maximal with this property.
We can show that:
|
|
Uses the first lemma today. □
Lemma.
Let without
common factors in . Then
the system of equations
has only finitely many solutions.
Proof.
(poynomials in
with coefficients in ).
have no common factors in .
Then Gauss’s lemma gives us that they have no common factors in .
This is because
is a UFD and
is its quotient field.
Since is a Euclidean
domain, there exists
such that
Multiply by the common denominator
of , and
we get
for some .
Hence the common solutions of
has finitely many -coordinates.
Then swap
and .
□
Theorem.
Let
homogeneous of degree ,
without repeated factors. Let
of degree . Assume
is irreducible in
. Then there are at most
finitely many solutions of
with .
.
.
,
.
.
.
.
a basis such
that .
.
Subspace Theorem: Let be
a vector space of dimension
over .
Let ,
be two
bases. there
exists such
that
that satisfies
|
|
then for
some .
Proof of Schinzel’s Theorem.
We show that
is finite for any .
Let be a
basis with .
Then
if . We
set to
be large enough so that this holds.
Recall the reference basis are
suitable monomials of degree ,
so
Then for ,
we have:
|
|
Hence
|
|
provided is
still large.
By the subspace theorem,
for some .
To apply the lemma, we need . This
can be assumed: indeed, multiplying
by an element of , we can make
the leading coefficient to be in ,
and all other coefficients will be algebraic integers. Then replace
by the
sum of its Galois conjugates. □
Theorem.
For
with ,
we write
for the order of the multiplicative group generated by
in .
Then:
|
|
Remark.
for ,
. Hence
|
|
Theorem (Corvaja, Zannier; Hernández, Luca).
Write
. Then
for all ,
there are only finitely many pairs of multiplicatively independent
such
that
|
|
are multiplicatively independent
if there does not exist
such that .
Fact: there exist infinitely many
such that
|
|
Theorem (1).
If ,
then
Theorem (2).
For all ,
there are only finitely many pairs of multiplicatively independent
such
that
|
|
Proof of Theorem 1 using Theorem 2.
Let
|
|
This is a subgroup of ,
and
The volume
is .
Our aim is to find
linearly idnependent and ,
where
is absolute.
If we can do this, then: .
By Theorem (2), since
and are
multiplicatively independent, we would get
Taking :
provided is sufficiently
large in terms of .
Now to the proof of the above stated aim: Let ññ
that generate and such that
their angle is as close to
as possible.
Then this angle is between
and :
The area of the parallelogram spanned by ñ
and ñ is
at least
|
ññ |
Minkowski’s second theorem in the geometry of numbers.
We know that ñ
or ñ. Then:
either ñ
or has to be
. In particular:
ñ (for some absolute
constant ).
Then ññ.
□
Proposition 1.14.
Let be a
linear form. Then there exists
such that any solution
of
satisfies
|
|
for some .
Remark.
For
such that
with ,
, then
Note that is invariant under
multiplication by elements of .
Theorem.
Let
be a vector space of dimension
over .
Let
be finite with .
For each ,
let
be a basis of .
Furthermore, let
be another basis. Fix an extension of each
from
to .
Then for all , there are
finitely many such
that all solutions
of
|
|
with satisfy
for
some .
Proof of Proposition.
By induction on .
Suppose .
As we observed the conclusion, is invariant under dividing
by the same element of .
Now .
So it is enough to prove for solutions with .
Let .
Then
with
implies
and .
So there are finitely many possibilities for
in terms of .
Pick
that works for all.
(to be continued). □
“generalised -unit
equations”.
Let be a
number field: .
Let be a finite
set containing :
(“-integers”).
units in
(“-units”).
Unit eqution
with
units.
Proof (continued).
Induction on .
was checked before.
Suppose , and the
claims hold for .
We make some simplifying assumptions to be specified later. We apply the subspace theorem on
. The reference
basis is ,
. As a first
approximation, we try
for all . Let
. Let
be a
solution of .
Then
|
|
We can replace
by
where .
Then we replace
by .
We do this for some choice .
Now back to the simplifying assumptions: We assume that
is maximal for .
Then .
So let
such that .
We may also assume .
For this, we may need to divide
by the common divisor, and rearrange the indices.
For these augmented ’s,
we get
|
|
So the subspace theorem applies with .
So
satisfies one of finitely many linear equations. Apply the induction hypothesis for each of them. □
Theorem 1.15.
For all ,
there exist finitely many multiplicatively independent pairs
such
that
|
|
Proof.
Fix some .
Let
multiplicatively independent and such that
|
|
Our goal is to show
for some .
Note: ,
because otherwise
or .
Then
and
would be a power of the same prime. Not possible due to multiplicative independence.
Fix some
sufficiently large depending on .
We apply the subspace theorem on .
We will evaluate our functionals at the point
where
is an enumeration of
for ,
such that ,
.
Note: . This
is because .
Also: for all
. The coordinates
on will be denoted
by . All our linear
forms on will be of
the form for some
. This is indeed
well defined on .
Reference basis .
|
|
For :
where
are multiplicatively
independent. We assume:
for some . Our
goal is to prove .
|
|
is an
enumeration of ,
.
|
|
Let’s take ,
.
|
|
.
Subspace theorem applies hence there exists a linear relation between
(distinct by multiplicative
independence of ).
Proposition implies
|
|
for some .
Then so
. However,
.
|
|
□
Theorem 1.16 (Feldman).
Let
of degree . Then
there exists effective
and such
that for all ,
Remark.
This is enough to solve ,
where is a
degree
homogeneous polynomial without repeated factors. Thue equation.
Proposition.
Let be a
number field. Then there exists
and and a
constant
such that ,
there exists
and
such that
Define (logarithmic embedding).
Note that here is the group
under multiplication, while
is the additive group.
For ,
. Then:
|
|
For ,
. So
Kronecker’s theorem:
are the roots of unity.
Dirichlet’s unit theorem:
is a lattice in
that is a -module
of rank which
spans .
Let be a fundamental
system of units, that is is
a basis for the lattice .
Fix some .
Pick some
such that
.
Then there exist
such that
|
|
There exists
such that .
Let with
and
. This
gives .
Take: .
|
|
is in a fixed,
compact region of .
.
|
|
Theorem.
algebraic of degree .
Then there exists ,
such that
for all :
Proof.
Fix some
and
small enough. Suppose that
for some .
We aim to show that .
We assume as we may that
is an algebraic integer.
Let
be the minimal polynomial of .
Then:
With .
Then
In particular:
Therefore: ,
such
that .
Then
Use .
Then is very close
to . Consider:
, which is similar
to both of
and .
Now more formally:
|
|
. Now
use the proposition:
Writing
we have:
|
|
. Take
to be the principal
branch, that is .
Warning: in general.
This is Lipschitz around ,
so we get
for a suitable ,
and .
Reminder:
Theorem.
Let .
Let , and let
be any choice
of the
of . Let
and let
.
Let
Then there exists an effective constant
(a function of and
the degree of )
such that
implies
|
|
So the lower bound gives:
We apply the theorem with .
,
.
.
. So
|
|
We still need to consider .
This is equivalent to:
|
|
Solving this equation gives
or .
Neither is the case.
If we use the weaker bound for ,
then we would prove:
|
|
˙