Set Systems - Combinatorics - Cambridge III notes

1 Set Systems

Definition 1 (Set system). Let $X$ be a set. A set system on $X$ (or a family of subsets of $X$ ) is a family $A \subset P (X)$ .

Notation. We will use the notation

X^{(r)} = {A \subset X : | A | = r} .

We call an element of $X^{(r)}$ an $r$ -set. We will usually be using $X = [n] = {1, \dots, n}$ , so $| X^{(r)} | = (\binom{n}{r})$ .

Example.

{[4]}^{(2)} = {12, 13, 14, 23, 24, 34} .

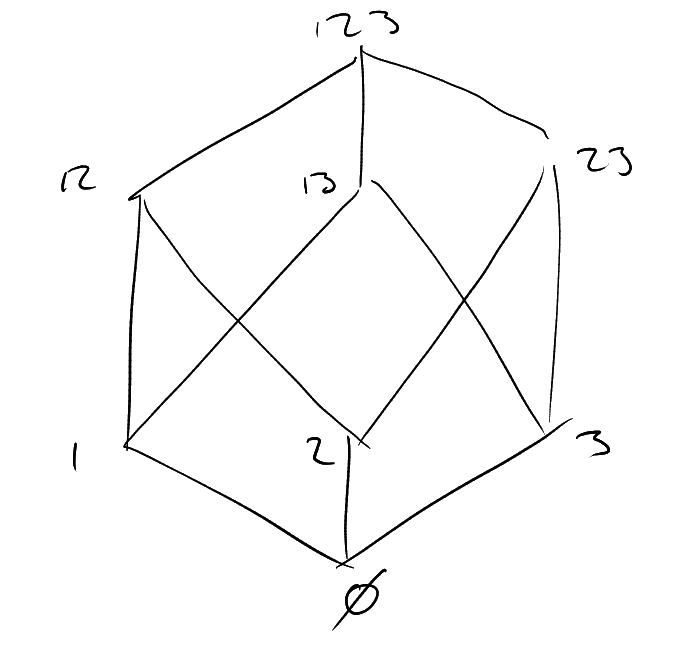
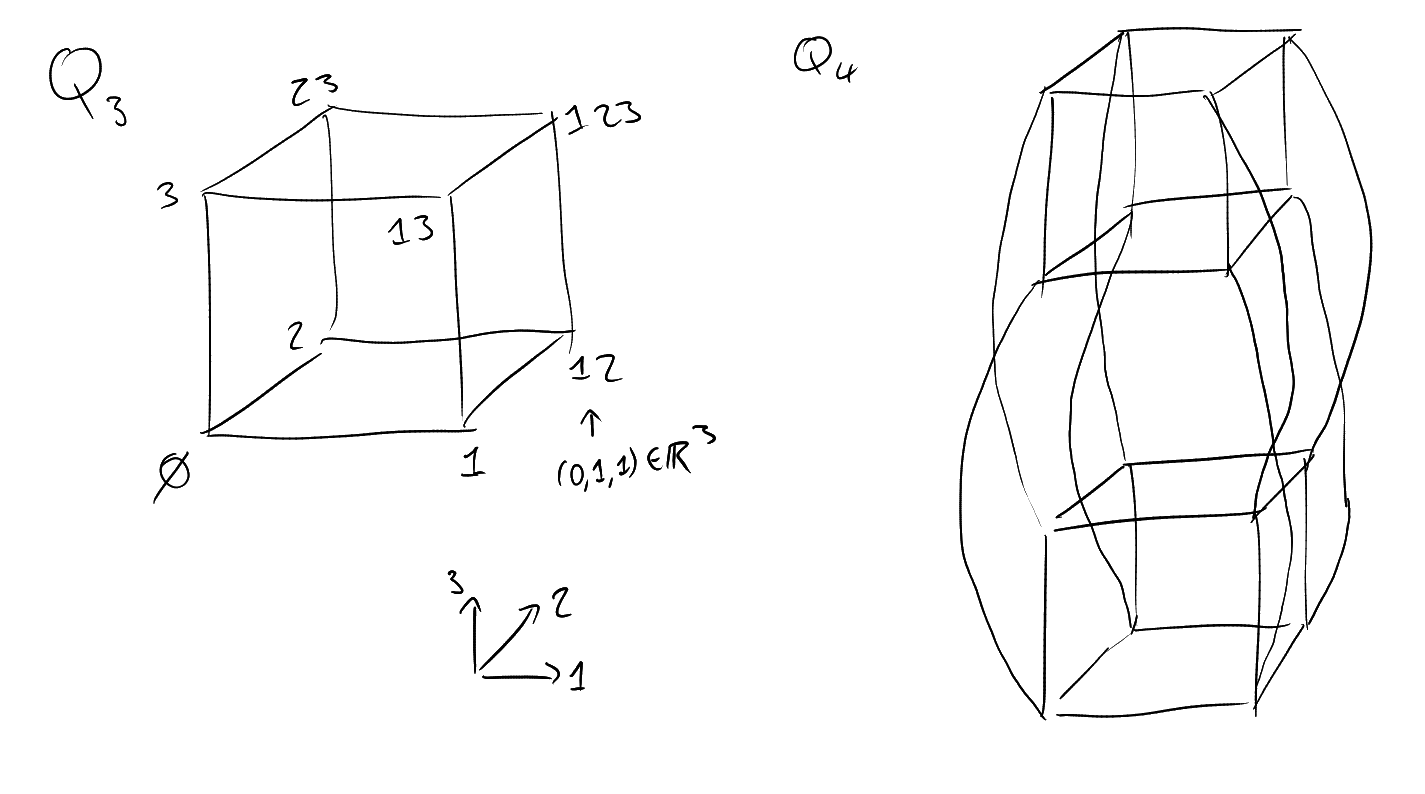
Definition 2 (Discrete cube). Make $P (X)$ into a graph by joining $A$ and $B$ if $| A Δ B | = 1$ , i.e. if $A = B \cup {i}$ for some $i$ , or vice versa. We call this ths discrete cube $Q_{n}$ (if $X = [n]$ ).

Example. $Q_{3}$ :

In general:

Alternatively, can view $Q_{n}$ as an $n$ -dimensional unit cube ${0, 1}^{n}$ , by identifying e.g. ${1, 3}$ with $1010000 \dots 0$ (i.e. identify $A$ with $𝟙_{A}$ , the characteristic function of $A$ ).

Example.

Definition 3 (Chain). Say $A \subset P (X)$ is a chain if $\forall A, B \in A$ , either $A \subset B$ or $B \subset A$ .

Example. For example,

A = {23, 12357, 123567}

is a chain.

Definition 4 (Antichain). Say $A$ is an antichain if $\forall A, B \in A$ , $A \neq B$ , we have $A ⁄ \subset B$ .

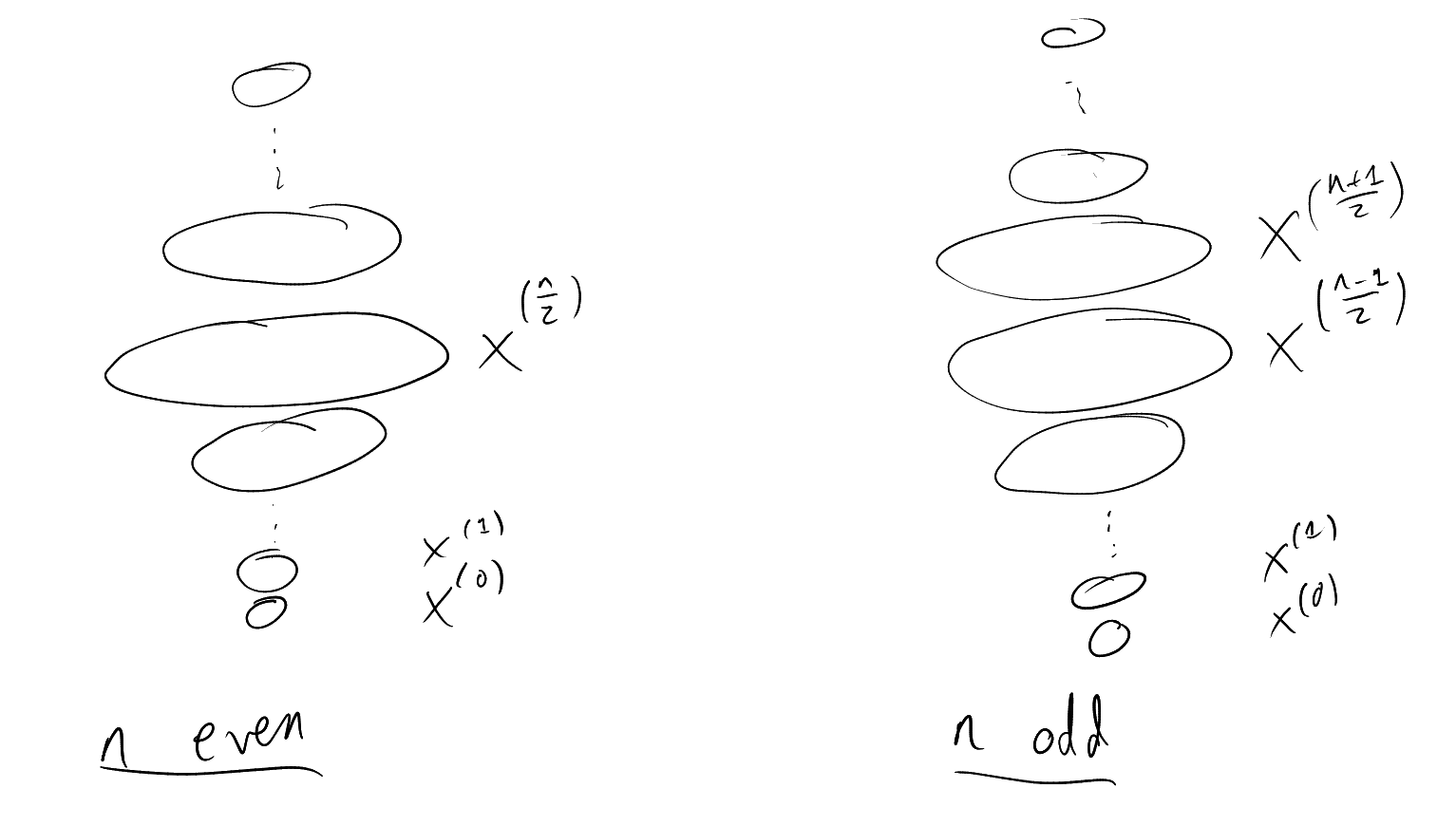
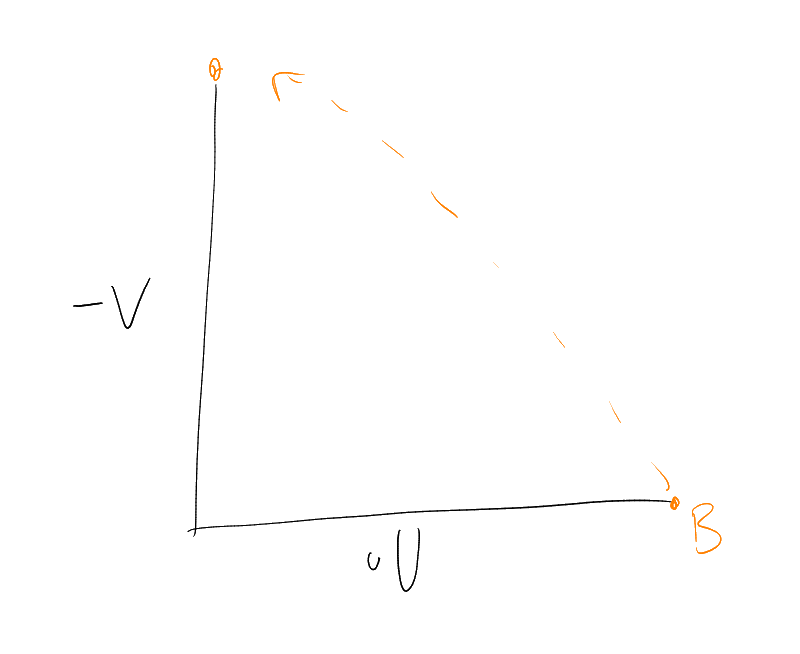
How large can a chain be? Can achieve $| A | = n + 1$ , for example using

A = {\emptyset, 1, 12, 123, \dots, [n]} .

Cannot beat this: for each $0 \leq r \leq n$ , $A$ contains $\leq 1$ $r$ -set.

How large can an antichain be? Can achieve $| A | = n$ , for example $A = {1, 2, \dots, n}$ . More generally, can take $A = X^{(r)}$ , for any $r$ – best out of these is $X^{(⌊ \frac{n}{2} ⌋)}$ .

Can we beat this?

Theorem 5 (Sperner’s Lemma). Assuming that:

$A \subset P (X)$ is an antichain

Then

| A | \leq (\binom{n}{⌊ \frac{n}{2} ⌋})

Idea: Motivated by “a chain meets each layer in $\leq 1$ point, because a layer is an antichain”, we will try to decompose the cube into chains.

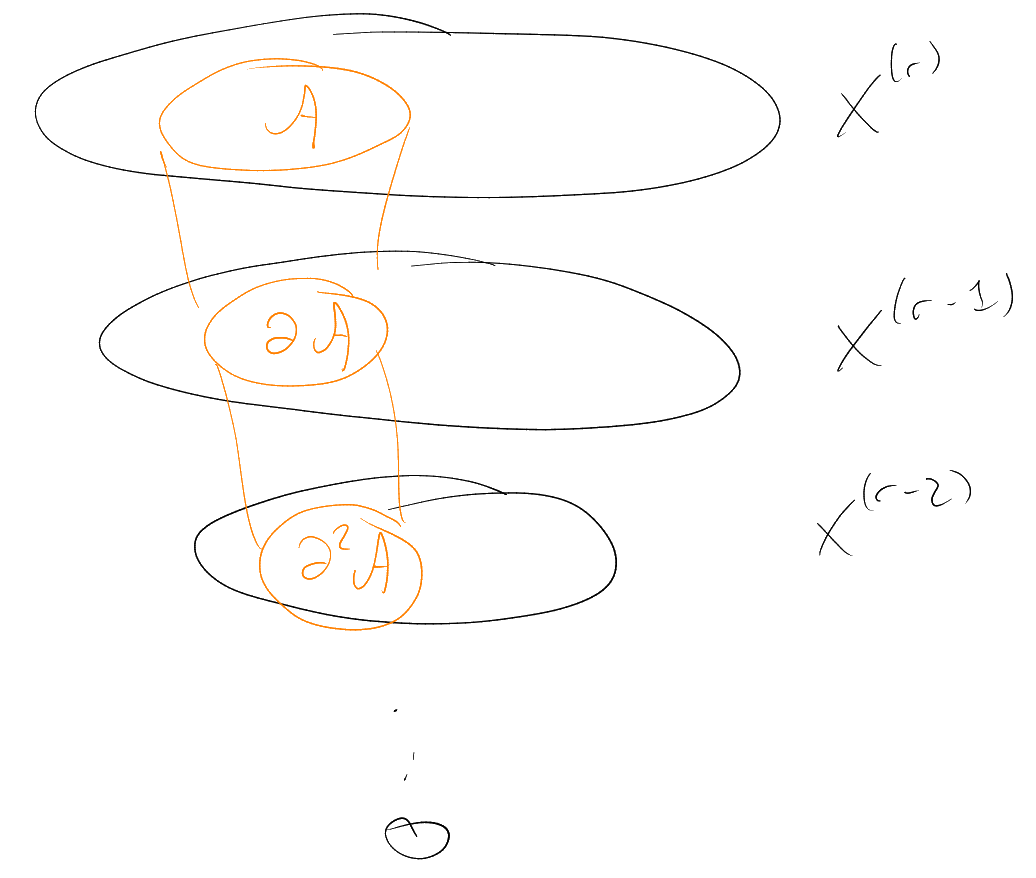
Proof. We’ll decompose $P (X)$ into $(\binom{n}{\frac{1}{2} n})$ chains – then done. To achieve this, it is sufficient to find:

(i) For each $r < ⌊ \frac{n}{2} ⌋$ , a matching from $X^{(r)}$ to $X^{(r + 1)}$ (recall that a matching here means a set of disjoint edges, one for each point in $X^{(r)}$ ).
(ii) For each $r > ⌊ \frac{n}{2} ⌋$ , a matching from $X^{(r)}$ to $^{(r - 1)}$ .

We then put these together to form our chains, each passing through $X^{(⌊ \frac{n}{2} ⌋)}$ .

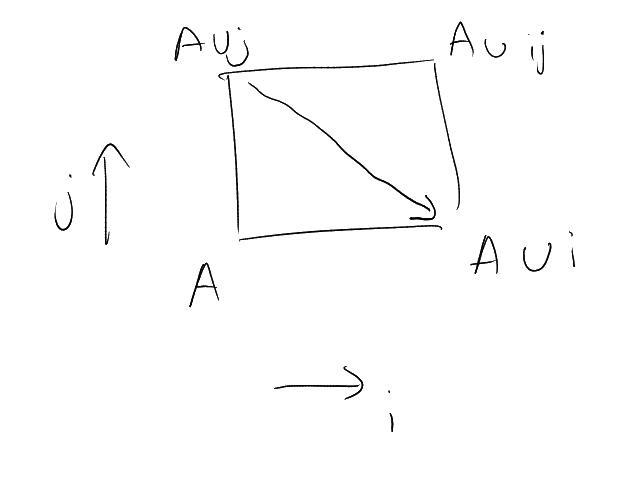
By taking complements, it is enough to prove (i).

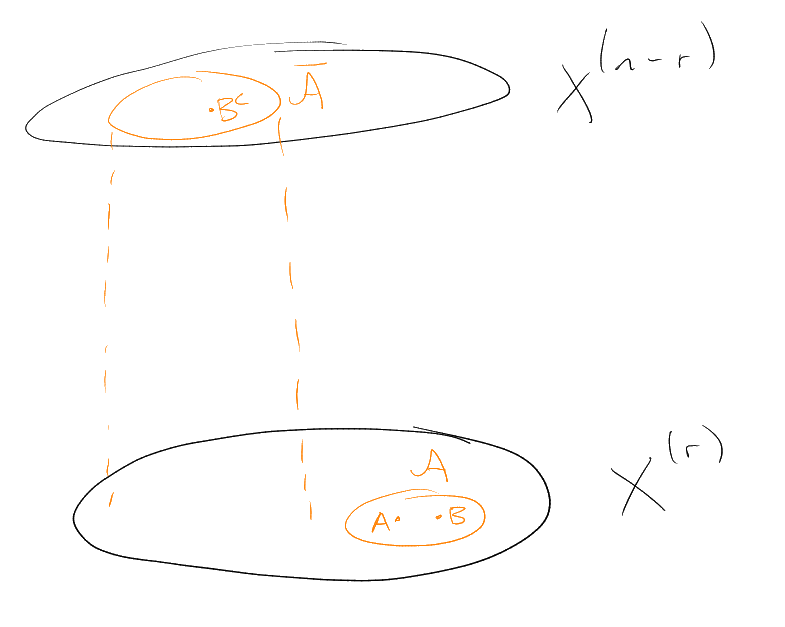
Let $G$ be the (bipartite) subgraph of $Q_{n}$ spanned by $X^{(r)} \cup X^{(r + 1)}$ : we seek a matching from $X^{(r)}$ to $X^{(r + 1)}$ . For any $S \subset X^{(r)}$ , the number of $S - Γ (S)$ edges in $G$ is $| S | (n - r)$ (counting from below) and $\leq | Γ (S) | (r + 1)$ (counting from above).

Hence, as $r < \frac{n}{2}$ ,

| Γ (S) | \geq \frac{| S | (n - r)}{r + 1} \geq | S | .

Thus by Hall’s Marriage theorem, there exists a matching. □

Equality in Sperner’s Lemma? Proof above tells us nothing.

Aim: If $A$ is an antichain then

\sum_{r = 0}^{n} \frac{| A \cap X^{(r)} |}{(\binom{n}{r})} \leq 1 .

“The percentages of each layer occupied add up to $\leq 1$ .”

Trivially implies Sperner’s Lemma (think about it).

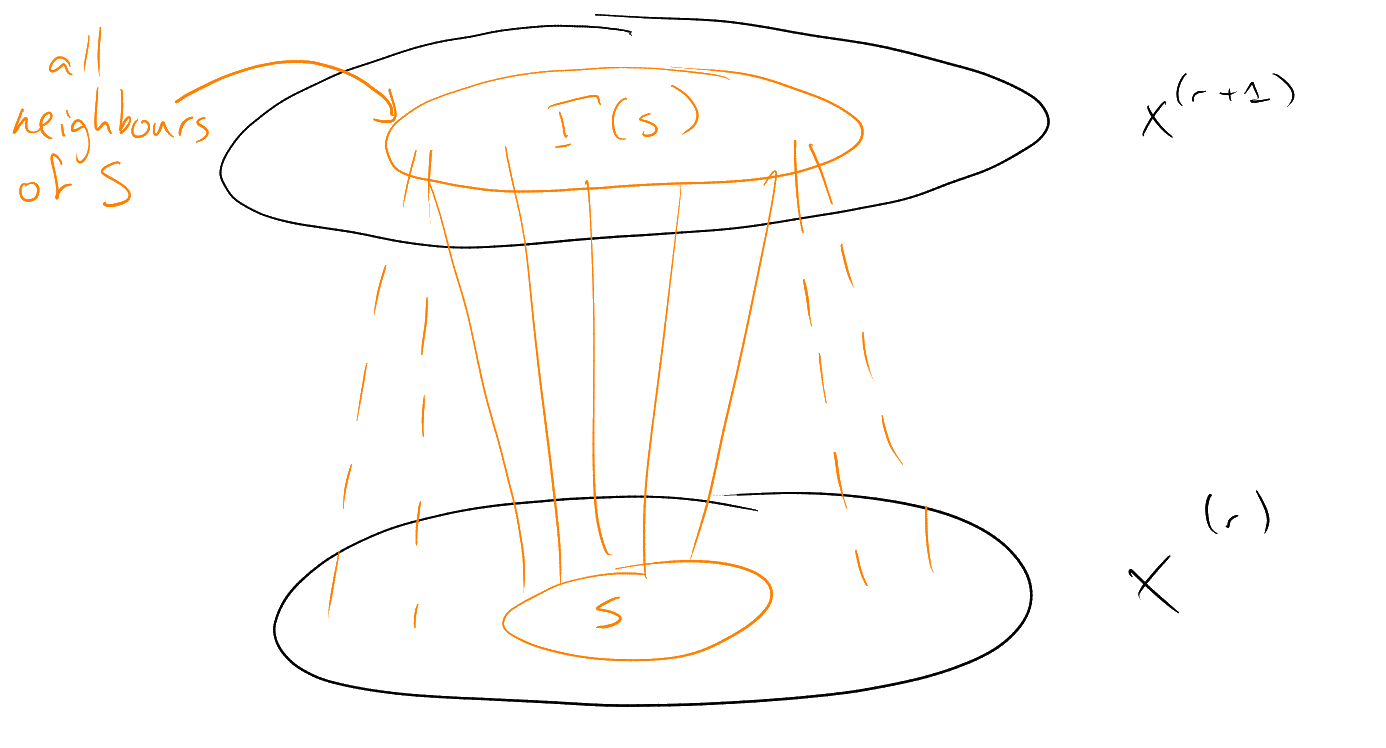
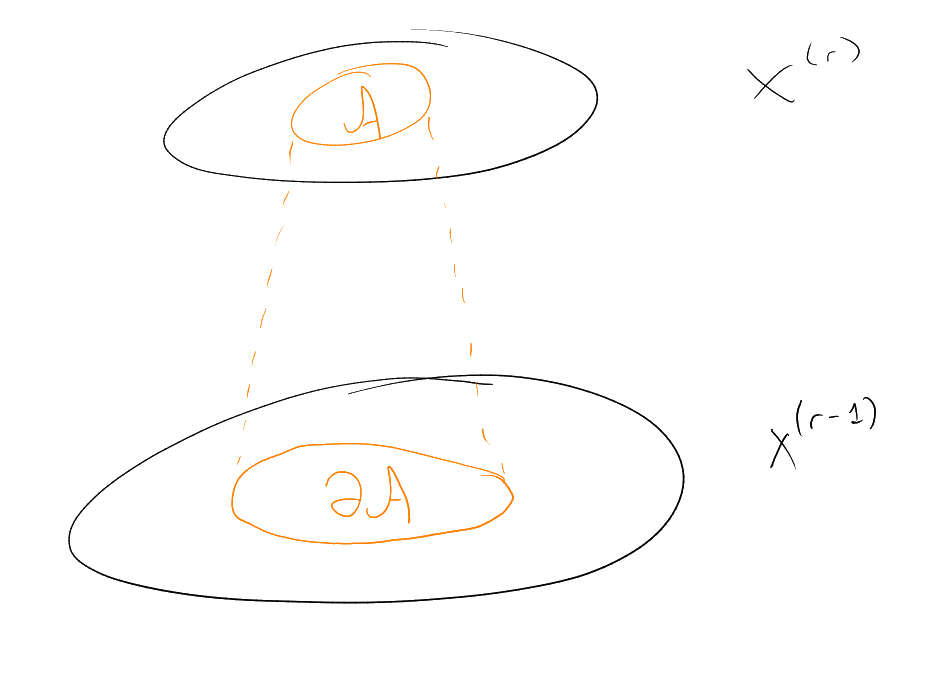
Definition 6 (Shadow). For $A \subset X^{(r)}$ ( $1 \leq r \leq n$ ), the shadow of $A$ is $\partial A = \partial^{-} A \subset X^{(r - 1)}$ defined by, $\partial A = {B \in X^{(r - 1)} : \exists A \in A, B \subset A}$ .

Example. If $A = {123, 124, 134, 137} \subset X^{(3)}$ , then $\partial A = {12, 13, 23, 14, 24, 34, 17, 37} \subset X^{(2)}$ .

Proposition 7 (Local LYM). Assuming that:

$A \subset X^{(r)}$
$1 \leq r \leq n$

Then

\frac{| \partial A |}{(\binom{n}{r - 1})} \geq \frac{| A |}{(\binom{n}{r})} .

“The fraction of the level occupied by $\partial A$ is $\geq$ the fraction for $A$ ”.

Remark. LYM = Lubell, Meshalkin, Yamamoto.

Proof. The number of $A - \partial A$ edges in $Q_{n}$ is $| A | r$ (counting from above) and is $\leq | \partial A | (n - r + 1)$ (counting from above). So

\frac{| \partial A |}{| A |} \geq \frac{r}{n - r + 1} .

But $\frac{(\binom{n}{r - 1})}{(\binom{n}{r})} = \frac{r}{n - r + 1}$ , so done. □

Equality in Local LYM? Must have that $\forall A \in A$ , $\forall i \in A$ , $\forall j \notin A$ have $A - {i} \cup {j} \in A$ . So $A = \emptyset$ or $X^{(r)}$ .

Theorem 8 (LYM Inequality). Assuming that:

$A \subset P (X)$ is an antichain

Then

\sum_{r = 0}^{n} \frac{| A \cap X^{(r)} |}{(\binom{n}{r})} \leq 1 .

Notation. We will now start writing $A_{r}$ for $A \cap X^{(r)}$ .

Proof 1. “Bubble down with Local LYM”.

Have $\frac{| A_{n} |}{(\binom{n}{n})} \leq 1$ . Now, $\partial A_{n}$ and $A_{n - 1}$ disjoint (as $A$ is an antichain), so

\frac{| \partial A_{n} |}{(\binom{n}{n - 1})} + \frac{| A_{n - 1} |}{(\binom{n}{n - 1})} = \frac{| \partial A_{n} \cup A_{n - 1} |}{(\binom{n}{n - 1})} \leq 1,

whence

\frac{| A_{n} |}{(\binom{n}{n})} + \frac{| A_{n - 1} |}{(\binom{n}{n - 1})} \leq 1

by Local LYM.

Now, note $\partial (\partial A_{n} \cup A_{n - 1})$ is disjoint from $A_{n - 2}$ (since $A$ is an antichain), so

\frac{| \partial (\partial A_{n} \cup A_{n - 1}) |}{(\binom{n}{n - 2})} + \frac{| A_{n - 2} |}{(\binom{n}{n - 2})} \leq 1,

whence

\frac{| \partial A_{n} \cup A_{n - 1} |}{(\binom{n}{n - 1})} + \frac{| A_{n - 2} |}{(\binom{n}{n - 2})} .

(Local LYM) so

\frac{| A_{n} |}{(\binom{n}{n})} + \frac{| A_{n - 1} |}{(\binom{n}{n - 1})} + \frac{| A_{n - 2} |}{(\binom{n}{n - 2})} \leq 1 .

Continue inductively. □

Equality in LYM Inequality? Must have had equality in each use of Local LYM. Hence equality in LYM Inequality needs: max $r$ with $A_{r} \neq \emptyset$ has $A_{r} = X^{(r)}$ .

So: equality in Local LYM $⟺$ $A = X^{(r)}$ for some $r$ .

Hence: equality in Sperner’s Lemma if and only if $A = X^{(r)} \frac{n}{2}$ (if $n$ even), and $A = X^{(⌊ \frac{n}{2} ⌋)}$ or $A = X^{(⌈ \frac{n}{2} ⌉)}$ .

Proof 2. Choose, uniformly at random, a maximal chain $C$ (i.e. $C_{0} \subset C_{1} \subset C_{2} \subset \dots \subset C_{n}$ , with $| C_{r} | = r$ for all $r$ ).

For any $r$ -set $A$ , $ℙ (A \in C) = \frac{1}{(\binom{n}{r})}$ (all $r$ -sets are equally likely). So $ℙ (C meets A_{r}) = \frac{| A_{r} |}{(\binom{n}{r})}$ (as events are disjoint) and hence

1 \geq ℙ (C meets A) = \sum_{r = 0}^{n} \frac{| A_{r} |}{(\binom{n}{r})} . □

Equivalently: (if you want to lose the intuition about how this works) then: $#maximal chains = n!$ , and $#through any fixed r -set = r! (n - r)!$ , hence

\sum_{r} | A_{r} | r! (n - r)! \leq n! .

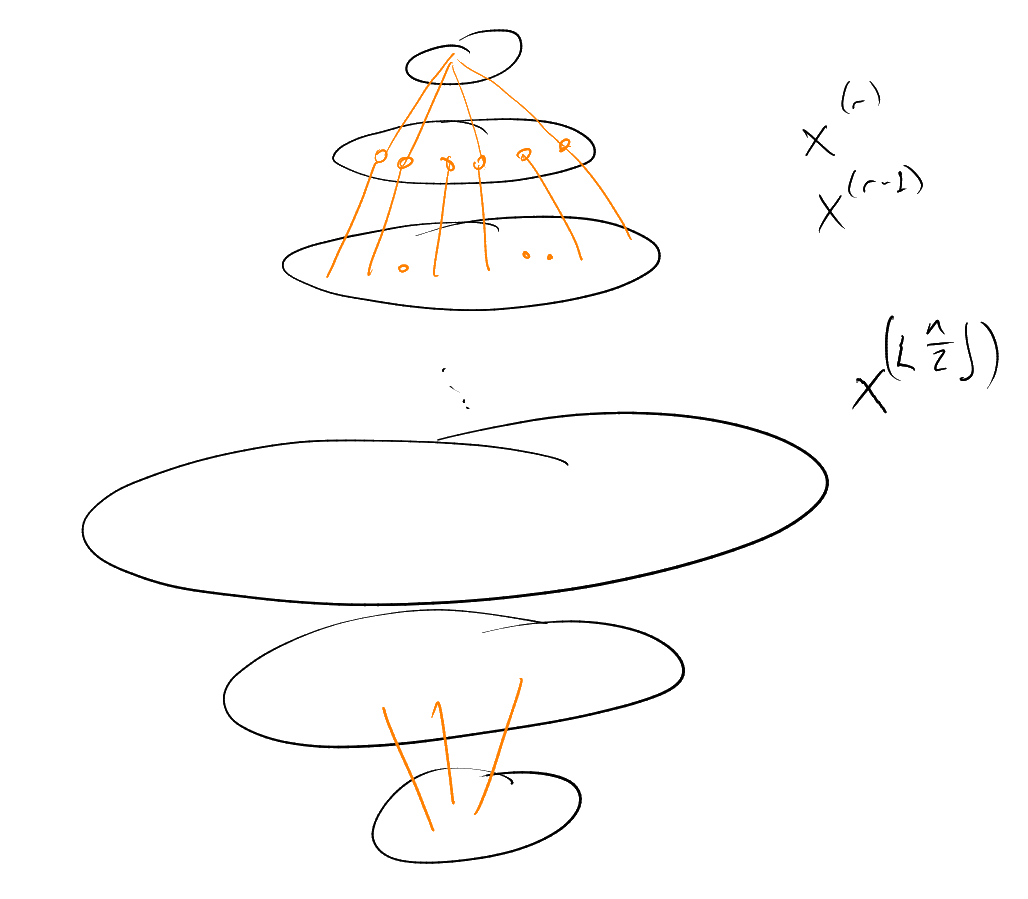
1.1 Shadows

For $A \subset X^{(r)}$ , know $| \partial A | \frac{r}{n - r + 1}$ . Equality is rare – only for $A = \emptyset$ or $X^{(r)}$ . What happens in between?

In other words, given $| A |$ , how should we choose $A \subset X^{(r)}$ to minimise $| \partial A |$ ?

Believable that if $| A | = (\binom{k}{r})$ then we sholud take $A = {[k]}^{(r)}$ .

What if $(\binom{k}{r}) < | A | < (\binom{k + 1}{r})$ ?

Believable that should take ${[k]}^{(r)}$ plus some $r$ -sets in ${[k + 1]}^{(r)}$ . For example, for $A \subset X^{(r)}$ with $| A | = (\binom{8}{3}) + (\binom{4}{2})$ , take $A = {[8]}^{(3)} \cup {9 \cup B : B \in {[4]}^{(2)}}$ .

1.2 Two total orders on $X^{(r)}$

Let $A$ and $B$ be distinct $r$ -sets: say $A = a_{1}, \dots, a_{r}$ , $B = b_{1}, \dots, b_{r}$ where $a_{1} < \dots < a_{r}$ and $b_{1} < \dots < b_{r}$ .

Say that $A < B$ in the lexicographic (or lex) ordering if for some $j$ we have $a_{i} = b_{i}$ for $i < j$ and $a_{j} < b_{j}$ .

Slogan: “Use small elements” (“dictionary order”).

Example. lexicographic on ${[4]}^{(2)}$ : $12, 13, 14, 23, 24, 34$ .

lexicographic on ${[6]}^{(3)}$ : $123, 124, 125, 126, 134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 256, 345$ , $346, 356, 456$ .

Say that $A < B$ in the colexicographic (or colex) ordering if for some $j$ we have $a_{i} = b_{i}$ for all $i > j$ and $a_{j} < b_{j}$ .

Slogan: “Avoid large elements” (note that this is not quite the same as “use small elements”, which is what we had before).

Example. colexicographic on ${[4]}^{(2)}$ : $12, 13, 23, 14, 24, 34$ .

colexicographic on ${[6]}^{(3)}$ : $123, 124, 134, 234, 125, 135, 235, 145, 245, 345, 126, 136, 236, 146, 246, 346$ , $156, 256, 356, 456$ .

Note that, in colexicographic, ${[n - 1]}^{(r)}$ is an initial segment (first $t$ elements, for some $t$ ) of ${[n]}^{(r)}$ .

This is false for lex.

So we could view colexicographic as an enumeration of $ℕ^{(r)}$ .

Remark. $A < B$ in colexicographic if and only if $A^{c} < B^{c}$ in “lexicographic with ground set order reversed”.

Aim: colexicographic initial segments are best for $\partial$ , i.e. if $A \subset X^{(r)}$ and $C \subset X^{(r)}$ is the initial segment of colexicographic with $| C | = | A |$ , then $| \partial C | \leq | \partial A |$ .

In particular, $| A | = (\binom{k}{r}) ⟹ | \partial A | \geq (\binom{k}{r - 1})$ .

1.3 Compressions

Idea: try to transform $A \subset X^{(r)}$ into some $A^{'} \subset X^{(r)}$ such that:

(i) $| A^{'} | = | A |$ .
(ii) $| \partial A^{'} | \leq | \partial A |$ .
(iii) $A^{'}$ looks more like’ $C$ than $A$ did.

Ideally, we’d like a family of such ‘compressions’: $A \to A^{'} \to A^{″} \to A^{‴} \to \dots \to B$ such that either $B = C$ or $B$ is so similar to $C$ that we can directly check that $| \partial B | \geq | \partial C |$ .

“colexicographic prefers 1 to 2” inspires:

Definition 9 ( $i j$ -compression). Fix $1 \leq i < j \leq n$ . The $i j$ -compression $C_{i j}$ is defined as follows:

For $A \in X^{(r)}$ , set

C_{i j} (A) = {\begin{matrix} A \cup i - j & if j \in A, i \notin A \\ A & otherwise \end{matrix},

and for $A \subset X^{(r)}$ , set

C_{i j} (A) = {C_{i j} (A) : A \in A} \cup {A \in A : C_{i j} (A) \in A} .

Note that the second part of the union in $C_{i j} (A)$ is because we need to make sure that we “replace $j$ by $i$ where possible”.

Example. If $A = {123, 134, 234, 235, 146, 567}$ then $C_{12} (A) = {123, 134, 234, 135, 146, 567}$ .

So $C_{i j} (A) \subset X^{(r)}$ , and $| C_{i j} (A) | = | A |$ .

Say $A$ is $i j$ -compressed if $C_{i j} (A) = A$ .

Lemma 10. Assuming that:

$A \subset X^{(r)}$
$1 \leq i < j \leq n$

Then

| \partial C_{i j} (A) | \leq | \partial A |

Proof. Write $A^{'}$ for $C_{i j} (A)$ . Let $B \in \partial A^{'} - \partial A$ . We’ll show that $i \in B$ , $j \notin B$ and $B \cup j - i \in \partial A - \partial A^{'}$ . [Then done].

Have $B \cup x \in A^{'}$ for some $x$ , with $B \cup x \notin A$ (as $B \notin \partial A$ ). So $i \in B \cup x$ , $j \notin B \cup x$ , and $(B \cup x) \cup j - i \in A$ .

Cannot have $x = i$ , else $(B \cup x) \cup j - i = B \cup j$ , giving $B \in \partial A$ , contradiction.

Hence we have $i \in B$ , $j \notin B$ .

Also, $B \cup j - i \in \partial A$ , since $(B \cup x) \cup j - i \in A$ .

Suppose $B \cup j - i \in \partial A^{'}$ : so $(B \cup j - i) \cup y \in A^{'}$ for some $y$ . Cannot have $y = i$ , else $B \cup j \in A^{'}$ – so $B \cup j \in A$ (as $j \in B \cup j$ ), contradicting $B \notin \partial A$ . Hence $j \in (B \cup j - i) \cup y$ and $i \notin (B \cup j - i) \cup y$ .

Whence both $(B \cup j - i) \cup y$ and $B \cup y$ belong to $A$ (by definition of $A^{'}$ ), contradicting $B \notin \partial A$ . □

Remark. Actually showed that $\partial C_{i j} (A) \subset C_{i j} \partial A$ .

Definition 11 (Left-compressed). Say $A \subset X^{(r)}$ is left-compressed if $C_{i j} (A) = A$ for all $i < j$ .

Corollary 12. Assuming that:

$A \subset X^{(r)}$ .

Then there exists a left-compressed

B \subset X^{(r)}

with

| B | = | A |

and

| \partial B | \leq | \partial A |

Proof. Define a sequence $A_{0}, A_{1}, \dots$ as follows. Set $A_{0} = A$ . Having defined $A_{0}, \dots, A_{k}$ , if $A_{k}$ left-compressed then stop the sequence with $A_{k}$ .

If not, choose $i < j$ such that $A_{k}$ is not $i j$ -compression, and set $A_{k + 1} = C_{i j} (A_{k})$ .

This must terminate, because for example $\sum_{A \in A_{k}} \sum_{i \in A}$ is strictly decreasing in $k$ .

Final term $B = A_{k}$ satisfies $| B | = | A |$ , and $| \partial B | \leq | \partial A |$ (by Lemma 10) □

Remark.

(1) Or: among all $B \subset X^{(r)}$ with $| B | = | A |$ and $| \partial B | \leq | \partial A |$ , choose one with minimal $\sum_{A \in B} \sum_{i \in A} i$ .
(2) Can choose order of the $C_{i j}$ so that no $C_{i j}$ applied twice.
(3) Any initial segment of colexicographic is left-compressed. Converse false, for example ${123, 124, 125, 126}$ (initial segment of lexicographic).

These compressions only encode the idea “colexicographic prefers $i$ to $j$ ( $i < j$ )”, but this is also true for lexicographic.

So we try to come up with more compressions that encode more of what colexicographic likes.

“colexicographic prefers $23$ to $14$ ” inspires:

Definition 13 ( $U V$ -compression). Let $U, V \subset X$ with $| U | = | V |$ , $U \cap V = \emptyset$ and $\max V > \max U$ . We define the $U V$ -compression as follows: for $A \subset X$ ,

C_{U V} (A) = {\begin{matrix} A \cup U - V & if V \subset A, U \cap A = \emptyset \\ A & otherwise \end{matrix},

and for $A \subset X^{(r)}$ , set

C_{U V} (A) = {C_{U V} (A) : A \in A} \cup {A \in A : C_{U V} \in A} .

Example. If

A = {123, 124, 147, 237, 238, 149},

then

C_{23, 14} (A) = {123, 124, 147, 237, 238, 239} .

So $C_{U V} (A) \subset X^{(r)}$ , and $| C_{U V} (A) | = | A |$ .

Say $A$ is $U V$ -compressed if $C_{U V} (A) = A$ .

Sadly, we can have $| \partial C_{U V} (A) | > | \partial A |$ :

Example. $A = {147, 157}$ has $| \partial A | = 5$ , but $C_{23, 14} (A) = {237, 147}$ has $| \partial C_{23, 14} (A) | = 6$ .

Despite this, we at least we do have the following:

Lemma 14. Assuming that:

$A \subset X^{(r)}$ is $U V$ -compression for all $U, V$ with $| U | = | V |$ , $U \cap V = \emptyset$ , $\max V > \max U$

Then

A

is an initial segment of colexicographic.

Proof. Suppose not. So there exists $A, B \in X^{(r)}$ with $B < A$ , in colexicographic but $A \in A$ , $B \notin A$ .

Put $V = A ∖ B$ , $U = B ∖ A$ .

Then $| V | = | U |$ , and $U, V$ disjoint, and $\max V > \max U$ (since $\max (A Δ B) \in A$ , by definition of colexicographic).

So $C_{U V} (A) = B$ , contradicting $A$ is $U V$ -compression. □

Lemma 15. Assuming that:

$U, V \subset X$
$| U | = | V |$
$U \cap V = \emptyset$
$\max U < \max V$
$A \subset X^{(r)}$
$\forall u \in U \exists v \in V such that A is (U - u, V - v) -compressed (∗)$

Then

| \partial C_{U V} (A) | \leq | \partial A |

Proof. Let $A^{'} = C_{U V} (A)$ . For $B \in \partial A^{'} - \partial A$ , we’ll show $U \subset B$ , $V \cap B = \emptyset$ , and $B \cup V - U \in \partial A - \partial A^{'}$ . (Then done).

Have $B \cup x \in A^{'}$ for some $x$ , and $B \cup x \notin A$ , so $U \subset B \cup x$ , $V \cap (B \cup x) = \emptyset$ , and $(B \cup x) \cup V - U \in A$ (by definition of $C_{U V}$ ).

If $x \in U$ : there exists $y \in V$ such that $A$ is $(U - x, V - y)$ -compressed, so from $(B \cup x) \cup V - U \in A$ we have $B \cup y \in A$ – contradicting $B \notin \partial A$ , contradiction.

Thus $x \notin U$ , and so $U \subset B$ , $V \cap B = \emptyset$ . Certainly $B \cup V - U \in \partial A$ (because $(B \cup x) \cup V - U \in A$ ), so just need to show that $B \cup V - U \notin \partial A^{'}$ .

Suppose $B \cup V - U \in \partial A^{'}$ : so $(B \cup V - U) \cup w \in A^{'}$ , for some $w$ . Also have $(B \cup V - U) \cup w \in A$ (for example, as $V$ contained in it).

If $w \in U$ : know $A$ is $(U - w, V - z)$ -compressed for some $z \in V$ , so $B \cup z \in A$ – contradicting $B \notin \partial$ .

If $w \notin U$ : have $V \subset (B \cup V - U) \cup w$ , $U \cap ((B \cup V - U) \cup w) = \emptyset$ , so by definition of $C_{U V}$ we must have that both $(B \cup V - U) \cup w$ and $B \cup w \in A$ – contradicting $B \notin \partial A$ , a contradiction. □

Theorem 16 (Kruskal-Katona). Assuming that:

$A \subset X^{(r)}$ , $1 \leq r \leq n$
$C$ is the initial segment of colexicographic on $X^{(r)}$ with $| C | = | A |$

Then

| \partial C | \leq | \partial A |

. In particular: if

| A | = (\binom{k}{r})

, then

| \partial A | \geq (\binom{k}{r - 1})

Proof. Let $Γ = {(U, V) : | U | = | V | > 0, U \cap V = \emptyset, \max U < \max V} \cup {(\emptyset, \emptyset)}$ . Define a sequence $A_{0}, A_{1}, \dots$ of set systems in $X^{(r)}$ as follows:

Set $A_{0} = A$ .
Having chosen $A_{0}, \dots, A_{k}$ , if $A_{k}$ is $U V$ -compressed for all $(U, V) \in Γ$ then stop. Otherwise, choose $U, V \in Γ$ with $| U | = | V | > 0$ minimal such that $A_{k}$ is not $U V$ -compressed.

Note that $\forall u \in U \exists v \in V$ such that $(U - u, V - v) \in Γ$ (namely, use $v = \min V$ ). So ( $*$ ) is satisfied.

So Lemma 15 tells us that $| \partial C_{U V} (A_{k}) | \leq | \partial A_{k} |$ .

Set $A_{k + 1} = C_{U V} (A_{k})$ , and continue.

Must terminate, as $\sum_{A \in A_{k}} \sum_{i \in A} 2^{i}$ is strictly decreasing. The final term $B = A_{k}$ satisfies $| B | = | A |$ , $| \partial B | \leq | \partial A |$ and is $U V$ -compressed for all $(U, V) \in Γ$ .

So $B = C$ by Lemma 14. □

Remark.

(1) Equivalently: if
$| A | = (\binom{k_{r}}{r}) + (\binom{k_{r - 1}}{r - 1}) + \dots + (\binom{k_{s}}{s}),$

where $k_{r} > k_{r - 1} > \dots > k_{s}$ , and $s \geq 1$ , then
$(\binom{| \partial A | \geq (\binom{k_{r}}{r - 1}) + (\binom{k_{r - 1}}{r - 2}) +}{+ (\binom{k_{s}}{s - 1}) .})$
(2) Equality in Kruskal-Katona? Can check that if $| A | = (\binom{k}{r})$ and $| \partial | = (\binom{k}{r - 1})$ (i.e. equality in a step of the proof of Kruskal-Katona), then $A = Y^{(r)}$ , for some $Y \subset X$ with $| Y | = k$ .
(3) However, not true in general that $| \partial A | = | \partial C |$ implies that $A$ is isomorphic to $C$ . (uset systems $A, B$ are isomorphic if there exists permutation of the ground set $X$ sending $A$ to $B$ ).

For $A \subset X^{(r)}$ , $0 \leq r \leq n$ , the upper shadow of $A$ is

\partial^{+} A = {A \cup x : A \in A, x \notin A} \subset X^{(r + 1)} .

Corollary 17. Assuming that:

$A \subset X^{(r)}$ , where $0 \leq r \leq n$
$C$ be the initial segment of lexicographic on $X^{(r)}$ with $| C | = | A |$

Then

| \partial^{+} A | \geq | \partial^{+} C |

Proof. From Kruskal-Katona, since $A < B$ in colexicographic if and only if $A^{c} < B^{c}$ in lexicographic with ground-set order reversed. □

Note that the shadow of an initial segment of colexicographic on $X^{(r)}$ is an initial segment of colexicographic on $X^{(r - 1)}$ – as if $C = {A \in X^{(r)} : A \leq a_{1} \dots a_{r} in colexicographic}$ then $\partial C = {B \in X^{(r - 1)} : B \leq a_{2} \dots a_{r} in colexicographic}$ .

This fact gives:

Corollary 18. Assuming that:

$A \subset X^{(r)}$ , and $C$ is the initial segment of colexicographic on $X^{(r)}$ with $| C | = | A |$

Then

| \partial^{t} C | \leq | \partial^{t} A |

for all

1 \leq t \leq r

Proof. If $| \partial^{t} C \leq | \partial^{t} A |$ , then $| \partial^{t + 1} C | \leq | \partial^{t + 1} A |$ , because $\partial^{t} C$ is an initial segment of colexicographic. Done by induction. □

Note. If $| A | = (\binom{k}{r})$ , then $| \partial^{t} A | \geq (\binom{k}{r - t})$ .

Remark. Proof of Kruskal-Katona used Lemma 14 and Lemma 15, but not Lemma 10 or Corollary 12.

1.4 Intersecting Families

Say $A \subset P (X)$ intersecting if $A \cap B \neq \emptyset$ for all $A, B \in A$ .

How large can an intersecting family be? Can have $| A | = 2^{k - 1}$ , by taking $A = {A : 1 \in A}$ .

Proposition 19. Assuming that:

$A \subset P (X)$ be intersecting

Then

| A | \leq 2^{k - 1}

Proof. For any $A \subset X$ , at most one of $A, A^{c}$ can belong to $A$ . □

Note. Many other extremal examples. For example, for $n$ odd take ${A : | A | > \frac{k}{2}}$ .

What if $A \subset X^{(r)}$ ?

If $r > \frac{n}{2}$ , take $A = X^{(r)}$ .

If $r = \frac{n}{2}$ : just choose one of $A, A^{c}$ for all $A \in X^{(r)}$ : gives $| A | = \frac{1}{2} (\binom{n}{r})$ .

So interesting case is $r < \frac{n}{2}$ .

Could try $A = {A \in X^{(r)} : 1 \in A}$ . Has size $(\binom{n - 1}{r - 1}) = \frac{r}{n} (\binom{n}{r})$ (while this identity can be verified by writing out factorials, a more useful way of observing it is by noting that $ℙ (random r -set contains 1) = \frac{r}{n}$ ).

Could also try $B = {A \in X^{(r)} : | A \cap {1, 2, 3} | \geq 2}$ .

Example. $n = 8$ , $r = 3$ . Then $| A | = (\binom{7}{2}) = 21$ and

| B | = \underset{| B \cap [3] | = 3}{\underset{⏟}{1}} + \underset{| B \cap [3] | = 2}{\underset{⏟}{(\binom{3}{2}) (\binom{5}{1})}} = 16 < 21 .

Theorem 20 (Erdos-Ko-Rado Theorem). Assuming that:

$A \subset X^{(r)}$ be intersecting, where $r < \frac{n}{2}$

Then

| A | \leq (\binom{n - 1}{r - 1})

Proof 1 (“Bubble down with Kruskal-Katona”). Note that $A \cap B \neq \emptyset ⟺ A ⁄ \subset B^{c}$ .

Let $\bar{A} = {A^{c} : A \in A} \subset X^{(n - r)}$ . Have $\partial^{n - 2 r} \bar{A}$ and $A$ are disjoint families of $r$ -sets.

Suppose $| A | > (\binom{n - 1}{r - 1})$ . Then $| \bar{A} | = | A | > (\binom{n - 1}{r - 1}) = (\binom{n - 1}{n - r})$ . Whence by Kruskal-Katona we have $| \partial^{n - 2 r} \bar{A} | \geq (\binom{n - 1}{r})$ .

So $| A | + | \partial^{n - 2 r} \bar{A} | > (\binom{n - 1}{r - 1}) + (\binom{n - 1}{r}) = (\binom{n}{r})$ , a contradiction. □

Remark. Calculation at the end had to give the right answer, as the $\partial$ calculations would all be exact if $A = {A \in X^{(r)} : 1 \in A}$ .

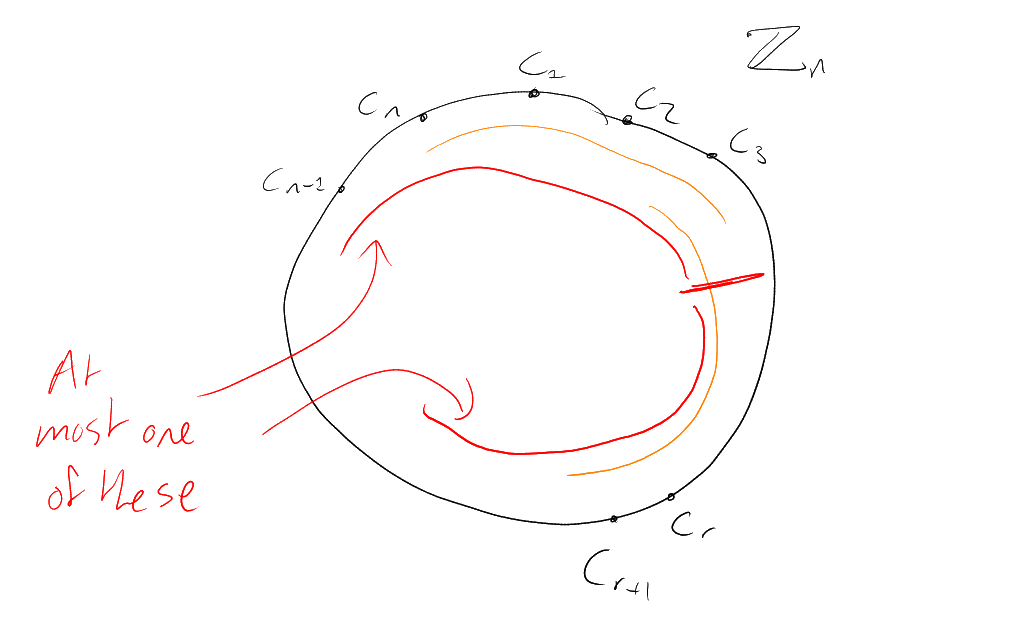
Proof 2. Pick a cyclic ordering of $[n]$ i.e. a bijection $c : [n] \to ℤ_{n}$ .

How many sets in $A$ are intervals ( $r$ consecutive elements) in this ordering?

Answer: $\leq r$ . Because say $C_{1}, \dots, C_{r} \in A$ . Then for each $2 \leq i \leq 1$ , at most one of the two intervals $C_{i} C_{i + 1} \dots C_{i + r - 1}$ and $C_{i - r} C_{i - r + 1} \dots C_{i - 1}$ can belong to $A$ (subscrpits are modulo $n$ ).

For each $r$ -set $A$ , in how many of the $n!$ cyclic orderings is it an interval?

Answer: $n r! (n - r)!$ ( $n =$ where, $r! =$ order inside $A$ , $(n - r)! =$ order outside $A$ ).

Hence $A | n r! (n - r)! \leq n! r$ , i.e. $| A | \leq \frac{n! r}{n r! (n - r)!} = (\binom{n - 1}{r - 1})$ . □

Remark.

(1) Numbers had to work out, given that we get equality $A = {A \in X^{(r)} : 1 \in A}$ .
(2) Equivalently, we are double-counting the edges in the bipartite graph, with vertex classes $A$ and all cycling orderings, with $A$ joined to $c$ if $A$ is an interval in $c$ .
(3) This method is caled averaging or Katona’s method.
(4) Equality in Erdos-Ko-Rado Theorem? Our example is actually unique – if $A \subset X^{(r)}$ is intersecting and $| A | = (\binom{n - 1}{r - 1})$ , then $A = {A \in X^{(r)} : i \in A}$ for some $1 \leq i \leq n$ .
Can get this from Proof 1 (and equality in Kruskal-Katona) or from Proof 2 (with a bit of care).

[next] [prev] [prev-tail] [front] [up]

1 Set Systems

1.1 Shadows

1.2 Two total orders on X(r)

1.3 Compressions

1.4 Intersecting Families

1.2 Two total orders on $X^{(r)}$