4 Further Topics
In , we
can do much better.
Theorem 4.1 (Ellenberg-Gijswijt, following Croot-Lev-Pach).
Assuming that:
Then .
Notation.
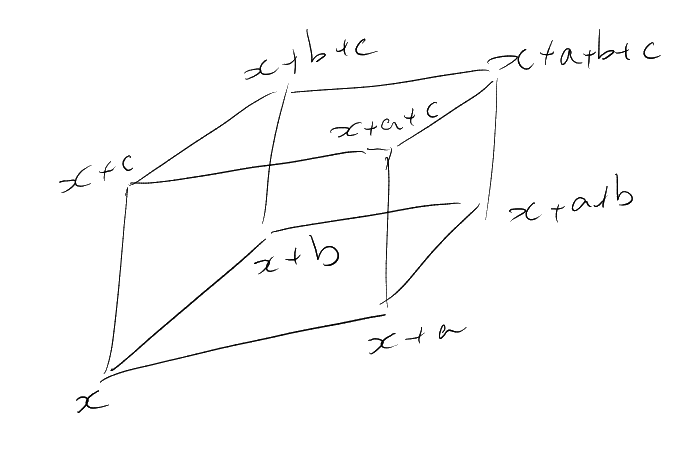
Let be the set of
monomials in whose degree
in each variable is at most .
Let be the vector
space over
whose basis is .
For any , write
for the set of
monomials in of (total)
degree at most , and
for the corresponding
vector space. Set .
Lemma 4.2.
Assuming that:
-
-
-
for all
Proof.
Every can be written as a
linear combination of monomials in ,
so
|
|
for some coefficients .
Clearly at least one of
must have degree ,
whence
|
|
for some families of polynomials ,
.
Viewing
as a -matrix
,
we see that
can be written as the sum of at most
matrices, each of which has rank .
Thus .
But by assumption,
is a diagonal matrix whose rank equals .
□
Proposition 4.3.
Assuming that:
Proof.
Let be an integer to
be determined later. Let be
the space of polynomials in
that vanish on .
We have
|
|
We claim that there exists
such that . Indeed, pick
with maximal support.
If , then there would be
a non-zero polynomial
vanishing on , in which
case , contradicting
the choice of .
Now by assumption,
So any polynomial that vanishes on
vanishes on .
By Lemma 4.2 we now have that,
Hence . But the
monomials in are in
bijection with the ones in
via , whence
. Thus
setting , we
have .
□
You will prove Theorem 4.1 on Example Sheet 3.
We do not have at present a comparable bound for 4 term arithmetic progressions. Fourier techniques also
fail.
Example 4.4.
Recall from Lemma 2.18 that given
,
|
𝟙𝟙𝟙𝟙 |
But it is impossible to bound
|
𝟙𝟙𝟙𝟙𝟙𝟙𝟙𝟙 |
by 𝟙. Indeed,
consider .
By Problem 11(ii) on Sheet 1,
and
|
𝟙 |
But given a 3 term arithmetic progression ,
by the identity
|
|
automatically
lies in ,
so
|
𝟙𝟙𝟙𝟙𝟙𝟙𝟙 |
which is not close to .
Definition 4.5 (-norm).
Given , define
its -norm by
the formula
|
|
Problem 1(i) on Sheet 2 showed that ,
so this is indeed a norm.
Problem 1(ii) asserted the following:
Lemma 4.6.
Assuming that:
Then |
|
Note that
|
|
and thus by Parseval’s identity,
|
|
Hence
|
|
Moreover, if 𝟙,
then
|
𝟙𝟙𝟙𝟙𝟙𝟙 |
We may therefore reformulate the first step in the proof of Meshulam’s Theorem as follows: if
, then
by Lemma 4.6,
|
|
It remains to show that if is non-trivial,
then there exists a subspace of
bounded codimension on which
has increased density.
Theorem 4.7 ( Inverse Theorem).
Assuming that:
-
-
-
-
Then there exists
such that
|
|
In other words,
for and
we say “
correlates with a linear phase function”.
Proof.
We have seen that
|
|
so
|
|
Definition 4.8 ( norm).
Given ,
define its
norm by
where and
denotes the
number of ones in .
It is easy to verify that
where .
Definition 4.9 ( inner product).
Given functions
for , define
their
inner product by
|
|
Observe that .
Lemma 4.10 (Gowers–Cauchy–Schwarz Inequality).
Assuming that:
Then |
|
Setting
for and
otherwise, it
follows that
hence .
Proposition 4.11.
Assuming that:
Then |
|
Proof.
We additionally assume
to make the proof easier to follow, but the same ideas are used for the general case. We additionally
assume ,
by rescaling, since the inequality is homogeneous.
Reparametrising, we have
Theorem 4.12 (Szemeredi’s Theorem for 4-APs).
Assuming that:
Then .
Idea: By Proposition 4.11 with 𝟙,
|
𝟙𝟙𝟙𝟙 |
where
consists of
other terms in which between one and three of the inputs are equal to
.
These are controlled by
whence
|
𝟙𝟙𝟙𝟙 |
So if contains no non-trivial 4
term arithmetic progressions and ,
then .
What can we say about functions with large
norm?
Example 4.13.
Let
be an symmetric
matrix with entries in .
Then
satisfies .
Theorem 4.14 ( inverse theorem).
Assuming that:
Then there exists a symmetric
matrix
with
entries in
and
such that
|
|
where is a
polynomial in .
In other words,
for and
we say “
correlates with a quadratic phase function”.
Proof (sketch).
Let
denote .
.
-
STEP 1:
Weak linearity. See reference.
-
STEP 2:
Strong linearity. We will spend the rest of the lecture discussing this in detail.
-
STEP 3:
Symmetry argument. Problem 8 on Sheet 3.
-
STEP 4:
Integration step. Problem 9 on Sheet 3.
STEP 1: If , then for
at least a -proportion
of ,
. So for each
such , there
exists such
that .
Proposition 4.15.
Assuming that:
-
-
-
-
Then there exists
with
and a
function
such that
-
(i)
;
-
(ii)
There are at least
quadruples
such that
and .
STEP 2: If and
are as above, then there
is a linear function
which coincides with
for many elements of .
Proposition 4.16.
Assuming that:
-
and
given as in Proposition
4.15
Then there exists
matrix
with
entries in
and
such
that
(
)
satisfies
for
elements
.
Proof.
Consider the graph of ,
.
By Proposition 4.15,
has
additive quadruples.
By Balog–Szemeredi–Gowers, Schoen, there exists
with
and .
udefine
by
and note .
By Freiman-Ruzsa applied to ,
there exists a subspace
with
such that .
Denote by the projection
onto the first coordinates.
By construction, .
Moreover, since ,
|
|
We may thus partition
into cosets of some
subspace such that
is injective on each coset. By
averaging, there exists a coset
such that
|
|
Set ,
and define
accordingly.
Now
is injective and surjective onto .
This means there is an affine linear map
such that
for all .
□
Then do steps 3 and 4. □
What to do if you have lots of additive quadruples?
Balog-Szemeredi-Gowers
What to do if you have small doubling constant?
Freiman-Ruzsa (or Polynomial-Freiman-Ruzsa)
˙