Categoricity - Model Theory - Cambridge III notes

For now, assume our theories have infinite models and that

κ \geq ℵ_{0} + | L |

Example 3.2.

$T h (ℕ)$ when $L = \emptyset$ is $κ$ -categorical for all $κ$ .
$T h (ℚ, +, 0)$ in $L_{group}$ is $κ$ -categorical if and only if $κ = ℵ_{0}$ .
$T h (ℚ, <)$ in $L_{o}$ is $κ$ -categorical if and only if $κ = ℵ_{0}$ .
$T h (ℤ, +, 0)$ in $L_{groups}$ is $κ$ -categorical for no $κ$ .

We do not prove this theorem in this course. The statement is examinable, but the proof is not.

Dense linear orders (with no endpoints)

Proof. Let $M, N ⊨ DLO$ with $M, N$ countable. We need to construct an $L$ -isomorphism $h : M \to N$ , i.e. an order preserving bijection.

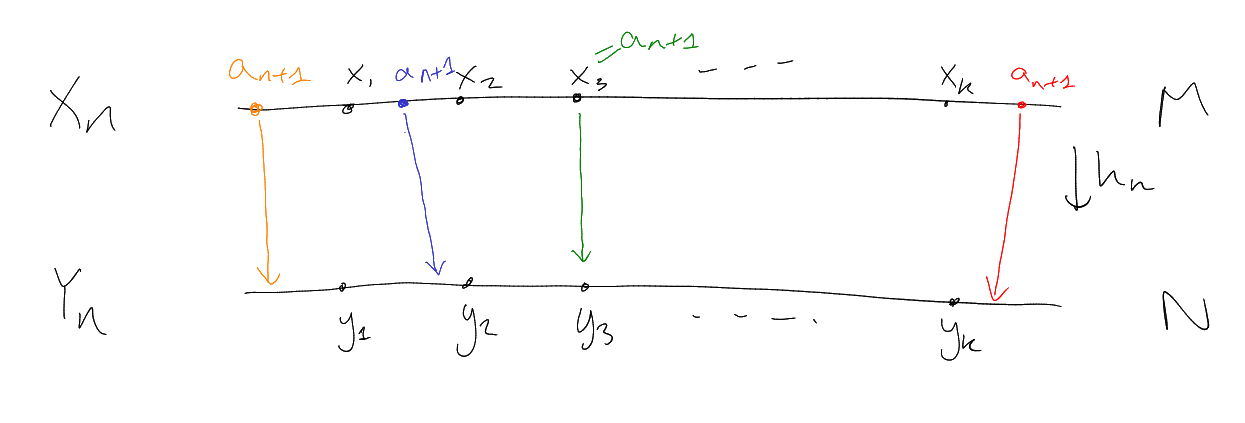
We will use the back and forth method.

Let $M = {a_{1}, a_{2}, \dots}$ and $N = {b_{1}, b_{2}, \dots}$ .

We construct a series of functions ${(h_{n})}_{n = 0}^{\infty}$ such that:

(i) $h_{n} : X_{n} \to Y_{n}$ is an order-preserving bijection.
(ii) $X_{n} \subseteq X_{n + 1}, Y_{n} \subseteq Y_{n + 1}, h_{n} \subseteq h_{n + 1}$ for each $n$ .
(iii) $a_{n} \in X_{n}$ , $b_{n} \in Y_{n}$ .

Once we have done this, $h = ⋃_{n = 0}^{\infty} h_{n}$ is an order-preserving bijection $h : M \to N$ (i.e. an $L$ -isomorphism).

Use induction.

Base case: $X_{0} = {x_{0}}$ , $Y_{0} = {b_{0}}$ , $h_{0} (a_{0}) = b_{0}$ .

Inductive step: Suppose $h_{n} : X_{n} \to Y_{n}$ as required.

“Forth”: Construct an order preserving bijection $h_{*} : X_{*} \to Y_{*}$ extending $h_{n}$ with $a_{n + 1} \in X_{*}$ . Enumerate $X_{n} = {x_{1}, \dots, x_{k}}$ with $x_{1} <^{M} x_{2} <^{M} x_{3} <^{M} \dots <^{M} x_{k}$ . Let $y_{i} = h (x_{i})$ so that $y_{1} <^{M} y_{2} <^{M} \dots <^{M} y_{k}$ .

Define $h_{*} = h_{n} \cup {(a_{n + 1}, b)}$ where $b \in N$ is chosen according to the following cases:

If $a_{n + 1} = x_{i}$ for some $i \in {1, \dots, k}$ , then put $b = x_{i}$ .
If $a_{n + 1} < x_{i}$ for all $i \in {1, \dots, k}$ then choose $b$ such that $b < y_{i}$ for all $i \in {1, \dots, k}$ (possible since no endpoints).
If $x_{i} < a_{n + 1}$ for all $i \in {1, \dots, k}$ , then choose $b$ such that $y_{i} < b$ for all $i \in {1, \dots, k}$ (possible since no endpoints).
If there is some $i \in {1, \dots, k - 1}$ such that $x_{i} < a_{n + 1} < x_{i + 1}$ , then choose $b$ such that $y_{i} < b < y_{i + 1}$ (possible since $M$ is dense).

Then $h_{*}$ is an order-preserving bijection and $a_{n + 1} \in X_{n + 1}$ as desired.

“Back”: We need to construct an order-preserving map $h_{n + 1} \to Y_{n + 1}$ extending $h_{*}$ with $b_{n + 1} \in Y_{n + 1}$ .

Exercise.

Then $h_{n + 1}$ satisfies the conditions. □

Consider

(ℝ, <)

, and consider

ℝ \times ℚ

with the lexicographic order (

(a, b) < (c, d)

if and only if

a < c

a = c

and

b < d

). These are both models of DLO (and have the same cardinality), but are not isomorphic (e.g. because the first does not have any countable intervals, or because the second does not have all bounded suprema).

3 Categoricity

Dense linear orders (with no endpoints)