Proof. Exercise: induction on the complexity of formulas. □

Proof.

• (i) $⟹$ (iii) Assume $T$ has quantifier elimination, and let $A$ be an $L$-structure. Suppose $M,N\models T\cup D(A)$. We want to show $M{\equiv }_{L_A}N$.

  Let $\sigma$ be an $L_A$-sentence, and suppose that $M\models \sigma$. Then $\sigma$ can be written as $\phi (\overline{a})$ where $\phi (\overline{x})$ is an $L$-formula and $\overline{a}\in A$.

  By quantifier elimination, we have $\psi (\overline{x})$ such that

  $$T\models \forall \overline{x}(\phi (\overline{x})\leftrightarrow \psi (\overline{x})).$$

  Now $M\models T$, so $M\models \forall \overline{x}(\phi (\overline{x})\leftrightarrow \psi (\overline{x}))$, and $M\models \phi (\overline{a})$. So $M\models \psi (\overline{a})$. Now $\psi (\overline{a})\in D(A)$ as $M\models D(A)$. So $N\models \psi (\overline{a})$, as $N\models D(A)$. Hence $N\models \phi (\overline{a})$ as $N\models T$ (i.e. $N\models \forall \overline{x}(\phi (\overline{x})\leftrightarrow \psi (\overline{x}))$). So $N\models \sigma$.

• (iii) $⟹$ (ii) Let $M,N\models T$, $A\subseteq M$, $A\subseteq N$. Let $\phi (\overline{x},y)$ be a quantifier free formula and let $\overline{a}\in A$ such that $M\models \exists y\phi (\overline{a},y)$.

  As $A\subseteq M$, $A\subseteq N$, we have $M,N\models T\cup D(A)$, so by (iii) we have $M{\equiv }_{L_A}N$ so $N\models \exists \phi (\overline{a},y)$.

• (ii) $⟹$ (i) We want to show quantifier elimination.

  By Lemma 11.3, it is sufficient to show for $\phi (\overline{x},y)$ quantifier free, we can find $\psi (\overline{x})$ quantifier free such that

  $$T\models \forall \overline{x}(\exists y,\phi (\overline{x},y)\leftrightarrow \psi (\overline{x})).$$

  Let $L^{\ast }=L\cup \{c_1,\dots ,c_n\}$ where each $c_i$ is a new constant (with $n=|\overline{x}|$). Let

  $$\mathrm{\Gamma }=\{\psi (\overline{x}):\psi (\overline{x})\text{ quantifier free formula such that }T\models \forall \overline{x},(\exists y,\phi (\overline{x},y)\to \psi (\overline{x}))\}.$$

  In definable sets:

  

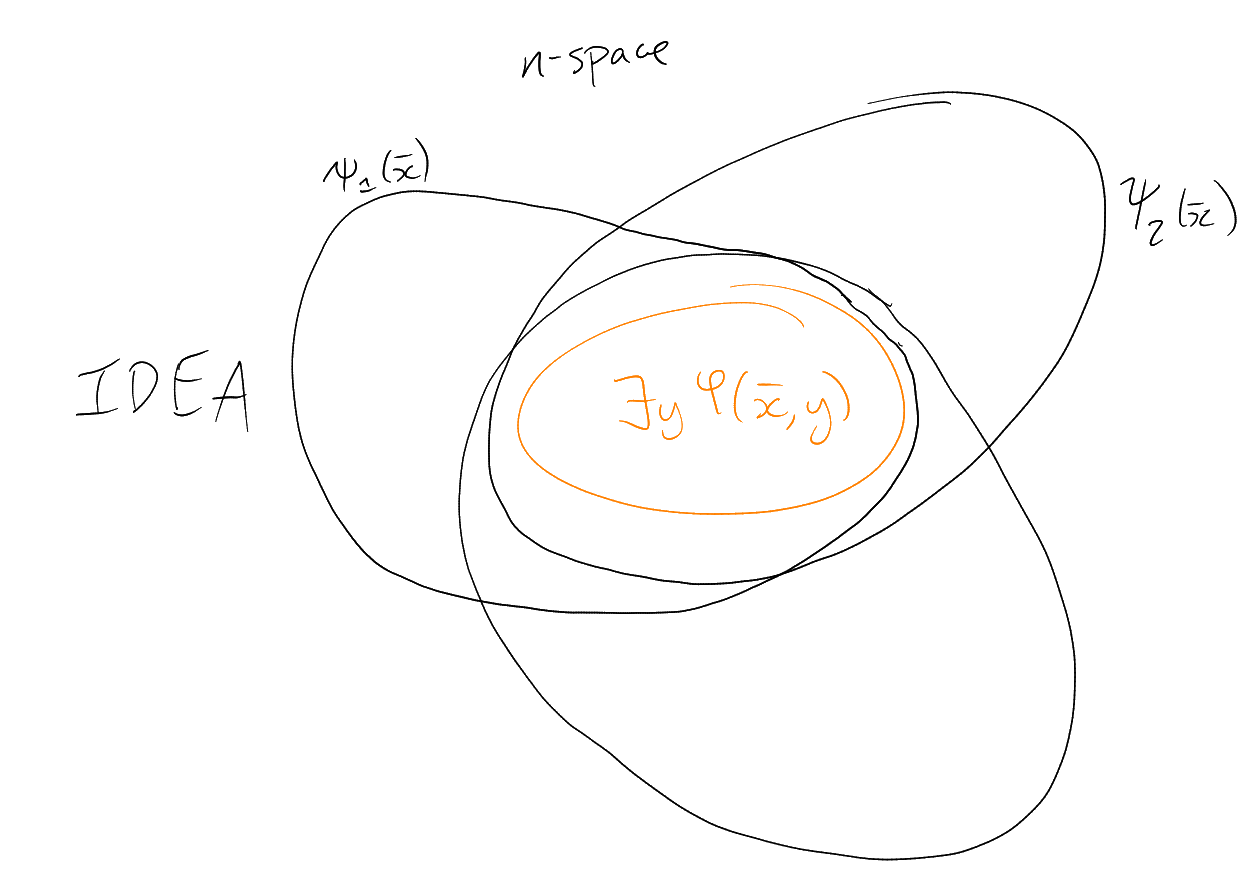
  Claim: $T\cup \mathrm{\Gamma }\models \exists y,\phi (\overline{x},y)$.

  Proof: Suppose not. Then there is an $L^{\ast }$-structure

  $$N\models T\cup \mathrm{\Gamma }\cup \{\neg \exists y,\phi (𝜀,y)\}.$$

  Let $a_i=c_i^N$, and let $A\subseteq N$ be the substructure generated by $a_1,\dots ,a_n$ in $N$.

  Then $N\models T$, $A\subseteq N$, $N\models \neg \exists y,\phi (\overline{c},y)$. Any $b\in A$ is of the form $t^N(\overline{a})$ for an $L$-term $t$ (exercise).

  So $D(A)$ can be viewed as an $L^{\ast }$-structure by replacing $\underline{b}$ ($b=t^N(\overline{a})$) with $t(\overline{c})$ in $L^{\ast }$. Let

  $$\mathrm{\Sigma }=T\cup D(A)\cup \{\exists y,\phi (\overline{x},y)\}.$$

  IDEA: build $M\models \mathrm{\Sigma }$, $M\models T\cup D(A)$ and $M\models \exists y,\phi (\overline{a},Y)$, contradicting (ii).

  Suffices to prove $\mathrm{\Sigma }$ is consistent.

  Assume $\mathrm{\Sigma }$ is inconsistent. Then by compactness we have ${\psi }_1(\overline{x}),\dots ,{\psi }_n(\overline{x})$ quantifier free $L$-formulas with

  • ${\psi }_1(\overline{c}),\dots ,{\psi }_m(\overline{c})\in D(A)$.

  • $T\cup \left\{{\wedge }_{i=1}^m{\psi }_i(\overline{c})\right\}\cup \{\exists y,\phi (\overline{c},y)\}$ is unsatisfiable.

  In definable sets:

  

  Let $\psi (\overline{x})$ be $\neg {\wedge }_{i=1}^m{\psi }_i(\overline{x})$, then $T\models \exists y,\phi (\overline{c},y)\to \psi (\overline{c})$.

  So $T\models \forall \overline{x}(\exists y,\phi (\overline{x},y)\to \psi (\overline{x}))$ so $\psi (\overline{c})\in \mathrm{\Gamma }$. So $N\models \psi (\overline{c})$ but also $N\models D(A)$ ($A\subseteq N$). Then

  $$N\models \underset{\in D(A)}{\underbrace{\underset{i=1}{\overset{m}{\wedge }}{\psi }_i(\overline{c})}}=\neg \psi (\overline{c})$$

  contradiction. So by compactness, $\mathrm{\Sigma }$ is consistent.

  This proves the claim.

  Reminder: the claim was that $T\cup \mathrm{\Gamma }\models \exists y,\phi (\overline{x},y)$. So by compactness, there are ${\psi }_1(\overline{x}),\dots ,{\psi }_m(\overline{x})$ quantifier free such that

  $$T\cup \underset{\subseteq \mathrm{\Gamma }}{\underbrace{\{\psi (\overline{c}),\dots ,{\psi }_m(\overline{c})\}}}\models \exists y,\phi (\overline{x},y).$$

  Recall

  $$T\models \forall \overline{x}(\exists y,\phi (\overline{x},y)\to \underset{i=1}{\overset{m}{\wedge }}{\psi }_i(\overline{x}))$$

  by choice of $n$. Let

  $$\psi (\overline{x})=\underset{i=1}{\overset{m}{\wedge }}{\psi }_i(\overline{x}).$$

  Then

  $$T\models \psi (\overline{c})\to \exists y,\phi (\overline{c},y)$$

  hence

  $$T\models \forall \overline{x}(\psi (\overline{x})\to \exists y,\phi (\overline{x},y)).$$

  Thus $T\models \forall \overline{x},(\psi (\overline{x})\leftrightarrow \exists y,\phi (\overline{x},y))$. □