Example.
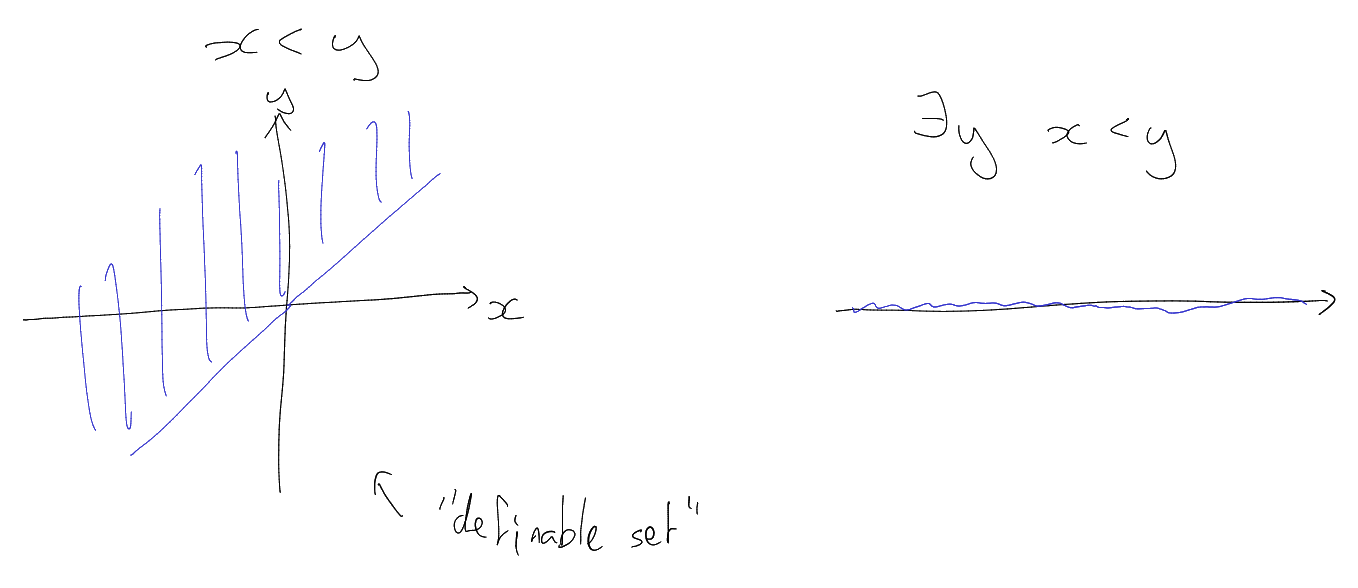
|
|
Example.
Convention: all languages include
Definition.
Given a language
|
|
Convention:
Terms: made of variables, constant symbols and function symbols in a ‘sensible way’
|
|
Atomic formulas: Plugging terms into one relation symbol
|
|
Formulas:
Boolean combinations (
Quantifiers (
in a ‘sensible way’:
|
|
A formula with
Example.

Formulas with no free variables are called sentences.
In an
True:
False:
In formula
Definition.
A set of sentences
Theorem (Compactness Theorem).
Let
(
Corollary (Upward Löwenheim Skolem). Any theory that has either:
arbitrary large finite models
at least one infinite model
has arbitrarily large models.