Bregman’s Theorem - Entropy Methods in Combinatorics

Let

G

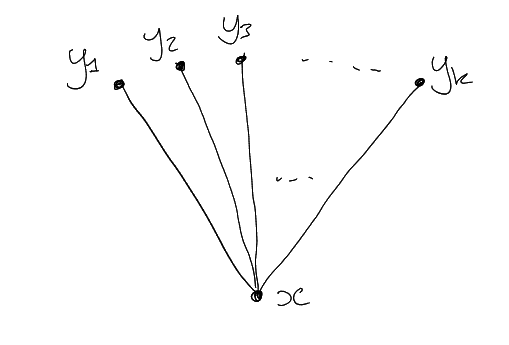
be a bipartite graph with vertex sets

X, Y

of size

n

. Given

(x, y) \in X_{Y}

, let

Brégman’s theorem concerns how large

per (A)

can be if

A

is a

01

-matrix and the sum of entres in the

i

-th row is

d_{i}

Let

G

be a disjoint union of

K_{a_{i} a_{i}}

s for

i = 1, \dots, k

, with

a_{1} + \dots + a_{k} = n

Proof (Radhakrishnan). Each matching corresponds to a bijection $σ : X \to Y$ such that $x σ (x) \in E (G)$ for every $x$ . Let $σ$ be chosen uniformly from all such bijections.

H [σ] = H [σ (x_{1})] + H [σ (x_{2}) | σ (x_{1})] + \dots + H [σ (x_{n}) | σ (x_{1}), \dots, σ (x_{n - 1})],

where $x_{1}, \dots, x_{n}$ is some enumeration of $X$ .

Then

\begin{array}{l} H [σ (x_{1})] & \leq \log d (x_{1}) \\ H [σ (x_{2}) | σ (x_{1})] & \leq 𝔼_{σ} \log d_{x_{1}}^{σ} (x_{2}) \end{array}

where

d_{x_{i}}^{σ} (x_{2}) = | N (x_{2}) ∖ {σ (x_{1})} | .

In general,

H [σ (x_{i}) | σ (x_{1}), \dots, σ (x_{i - 1})] \leq 𝔼_{σ} \log d_{x_{1}, \dots, x_{i - 1}}^{σ} (x_{i}),

where

d_{x_{1}, \dots, x_{i - 1}}^{σ} (x_{i}) = | N (x_{i}) ∖ {σ (x_{1}), \dots, σ (x_{i - 1})} | .

Key idea: we now regard $x_{1}, \dots, x_{n}$ as a random enumeration of $X$ and take the average.

For each $x \in X$ , define the contribution of $x$ to be

\log (d_{x_{1}, \dots, x_{i - 1}}^{σ} (x_{i}))

where $x_{i} = x$ (note that this “contribution” is a random variable rather than a constant).

We shall now fix $σ$ . Let the neighbours of $x$ be $y_{1}, \dots, y_{k}$ .

Then one of the $y_{j}$ will be $σ (x)$ , say $y_{h}$ . Note that $d_{x_{1}, \dots, x_{i - 1}}^{σ} (x_{i})$ (given that $x_{i} = x$ ) is

d (x) - | {j : σ^{- 1} (y_{j}) comes earlier than x = σ^{- 1} (y_{h})} | .

All positions of $σ^{- 1} (y_{h})$ are equally likely, so the average contribution of $x$ is

\frac{1}{d (x)} (\log d (x) + \log (d (x) - 1) + \dots + \log 1) = \frac{1}{d (x)} \log (d (x)!) .

By linearity of expectation,

H [σ] \leq \sum_{x \in X} \frac{1}{d (x)} \log (d (x)!),

so the number of matchings is at most

\prod_{x \in X} {(d (x)!)}^{\frac{1}{d (x)}} . □

Proof (Alon, Friedman). Let $M$ be the set of $1$ -factors of $G$ , and let $(M_{1}, M_{2})$ be a uniform random element of $M^{2}$ . For each $M_{1}, M_{2}$ , the union $M_{1} \cup M_{2}$ is a collection of disjoint edges and even cycles that covers all the vertices of $G$ .

Call such a union a cover of $G$ by edges and even cycles.

If we are given such a cover, then the number of pairs $(M_{1}, M_{2})$ that could give rise to it is $2^{k}$ , where $k$ is the number of even cycles.

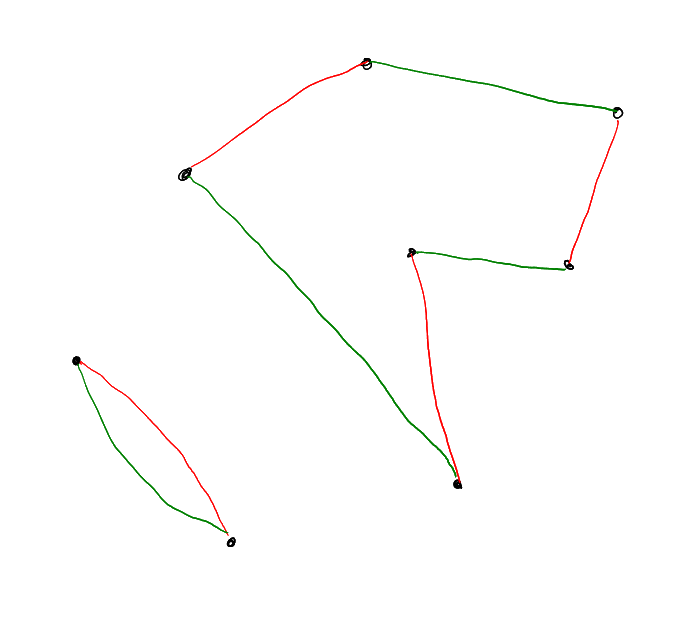
Now let’s build a bipartite graph $G_{2}$ out of $G$ . $G_{2}$ has two vertex sets (call them $V_{1}, V_{2}$ ), both copies of $V (G)$ . Join $x \in V_{1}$ to $y \in V_{2}$ if and only if $x y \in E (G)$ .

For example:

By Brégman, the number of perfect matchings in $G_{2}$ is $\leq \prod_{x \in V (G)} {(d (x)!)}^{\frac{1}{d (x)}}$ . Each matching gives a permutation $σ$ of $V (G)$ , such that $x σ (x) \in E (G)$ for every $x \in V (G)$ .

Each such $σ$ has a cycle decomposition, and each cycle gives a cycle in $G$ . So $σ$ gives a cover of $V (G)$ by isolated vertices, edges and cycles.

Given such a cover with $k$ cycles, each edge can be directed in two ways, so the number of $σ$ that give rise to is is $2^{k}$ , where $k$ is the number of cycles.

So there is an injection from $M^{2}$ to the set of matchings of $G_{2}$ , since every cover by edges and even cycles is a cover by vertices, edges and cycles.

| M |^{2} \leq \prod_{x \in V (G)} {(d (x)!)}^{\frac{1}{d (x)}} . □

3 Brégman’s Theorem