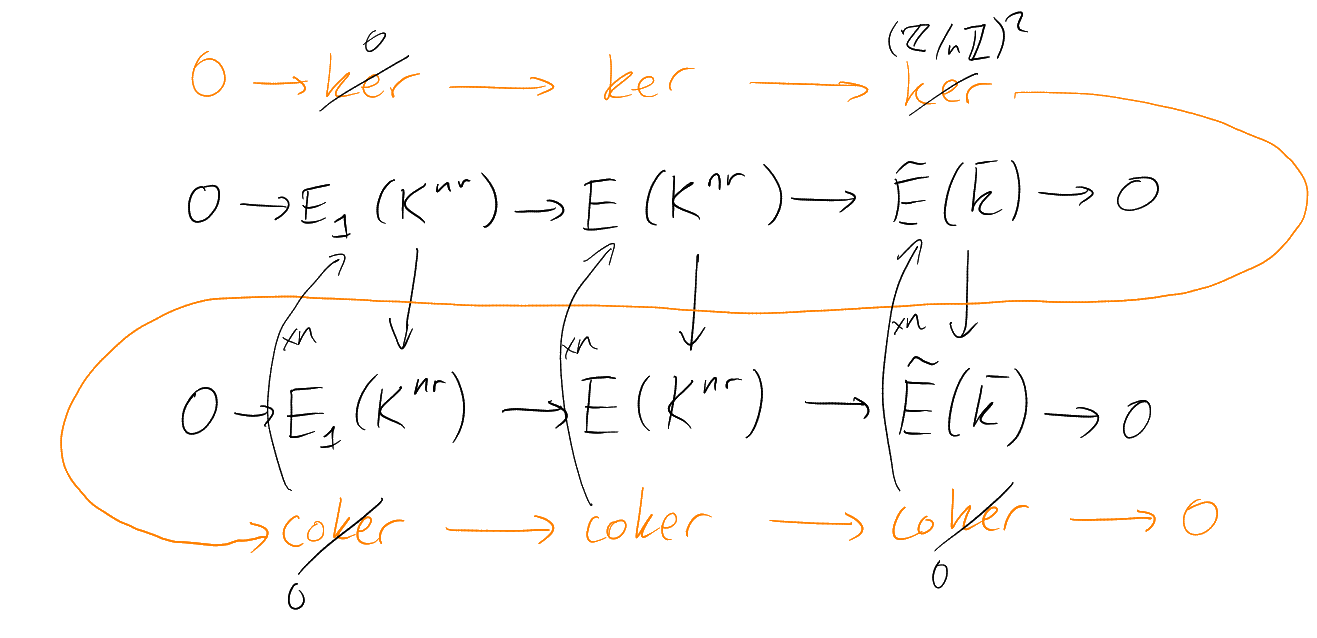Elliptic Curves over Local Fields - Elliptic Curves

9 Elliptic Curves over Local Fields

Let $K$ be a field, complete with respect to discrete valuation $v : K^{*} \to ℤ$ .

Notation. Valuation ring (= ring of integers) will be denoted by

O_{K} = {x \in K^{*} | v (x) \geq 0} \cup {0} .

Unit group will be denoted by

O_{K}^{*} = {x \in K^{*} | v (x) = 0} .

The maximal ideal will be denoted by $π O_{K}$ where $v (π) = 1$ .

The residue field will be denoted by $k = O_{K} ∕ π O_{K}$ .

We assume $char K = 0$ and $char k = p > 0$ . For example, $K = ℚ_{p}$ , $O_{K} = ℤ_{p}$ , $k = 𝔽_{p}$ .

Let $E ∕ K$ be an elliptic curve.

Definition (Integral / minimal Weierstrass equation). A Weierstrass equation for $E$ with coefficients $a_{1}, \dots, a_{6} \in K$ is integral if $a_{1}, \dots, a_{6} \in O_{K}$ and minimal if $v (Δ)$ is minimal among all integral Weierstrass equations for $E$ .

Remark.

(i) Putting $x = u^{2} x^{'}$ , $y = u^{3} y^{'}$ gives $a_{i} = u^{i} a_{i}^{'}$ . Therefore integral Weierstrass equations exist.
(ii) $a_{1}, \dots, a_{6} \in O_{K} ⟹ Δ \in O_{K} ⟹ v (Δ) \geq 0$ . Therefore minimal Weierstrass equations exist.
(iii) If $char k \neq 2, 3$ then there exists minimal Weierstrass equation of the form $y^{2} = x^{3} + a x + b$ .

Lemma 9.1. Assuming that:

$E ∕ K$ have integral Weierstrass equation
$y^{2} + a_{1} x y + a_{3} y = x^{3} + a_{2} x^{2} + a_{4} x + a_{6}$
$0 \neq P = (x, y) \in E (K)$

Then either

x, y \in O_{K}

{\begin{matrix} v (x) = - 2 s \\ v (y) = - 3 s \end{matrix}

for some $s \geq 1$ .

(Compare with Q5 from Example Sheet 1)

Proof. Throughout this proof, LHS and RHS refer to the Weierstrass equation of the curve.

Case $v (x) \geq 0$ :. If $v (y) < 0$ then $v (LHS) < 0$ and $v (RHS) \geq 0$ . Therefore $x, y \in O_{K}$ .

Case $v (x) < 0$ : $v (LHS) \geq \min (2 v (y), v (x) + v (y), v (y))$ and $v (RHS) = 3 v (x)$ . We get 3 possible inequalities from this, and each of them gives $v (y) < v (x)$ .

Now

\begin{array}{l} v (LHS) & = 2 v (y) \\ v (RHS) & = 3 v (x) \end{array}

{\begin{matrix} v (x) = - 2 s \\ v (y) = - 3 s \end{matrix}

for some $s \geq 1$ . □

If $K$ is complete, then $O_{K}$ is complete with respect to $π^{r} O_{K}$ (for any $r \geq 1$ ).

We fix a minimal Weierstrass equation for $E ∕ K$ . Get formal group $Ê$ over $O_{K}$ .

Taking $I = π^{r} O_{K}$ (with $r \geq 1$ ) in Lemma 8.2 gives

\begin{array}{l} Ê (I) & = {(x, y) \in E (K) | - \frac{x}{y}, - \frac{1}{y} \in π^{r} O_{K}} \cup {0} \\ = {(x, y) \in E (K) | v (\frac{x}{y}) \geq r, v (\frac{1}{y}) \geq r} \cup {0} \\ = {(x, y) \in E (K) | v (x) = - 2 s, v (y) = - 3 s for s \geq r} \cup {0} & (using Lemma 9.1) \\ = {(x, y) \in E (K) | v (x) \leq - 2 r, v (y) \leq - 3 r} \cup {0} & (using Lemma 9.1) \end{array}

By Lemma 8.2 this is a subgroup of $E (K)$ , say $E_{r} (K)$ .

\dots \subset E_{2} (K) \subset E_{1} (K) \subset E (K) .

More generally, for $F$ a formal group over $O_{K}$

\dots \subset F (π^{2} O_{K}) \subset F (π O_{K}) .

We claim that

$F (π^{r} O_{K}) ≅ (O_{K}, +)$ for $r$ sufficiently large.
$\frac{F (π^{r} O_{K})}{F (π^{r + 1} O_{K})} ≅ (k, +)$ for $r \geq 1$ .

Reminder: $char K = 0$ , $char k = p > 0$ .

Theorem 9.2. Assuming that:

$K$ a local field with $char K = 0$ , $char k = p > 0$
$F$ a formal group over $O_{K}$
$e = v (p)$
$r > \frac{e}{p - 1}$

Then

\log : F (π^{r} O_{K}) \to_{}^{≅} {\hat{𝔾}}_{a} (π^{r} O_{K})

is an isomorphism of groups with inverse

\exp : {\hat{𝔾}}_{a} (π^{r} O_{K}) \to_{}^{≅} F (π^{r} O_{K}) .

Remark. ${\hat{𝔾}}_{a} (π^{r} O_{K}) = (π^{r} O_{K}, +) ≅ (O_{K}, +)$ , $x \leftrightarrow π^{- r} x$ .

Proof. For $x \in π^{r} O_{K}$ we must show the power series $\log (x)$ and $\exp (x)$ converge to elements in $π^{r} O_{K}$ .

Recall

\exp (T) = T + \frac{b_{2}}{2!} T^{2} + \frac{b_{3}}{3!} T^{3} + \dots

for some $b_{i} \in O_{K}$ .

Claim: $v_{p} (n!) \leq \frac{n - 1}{p - 1}$ .

Proof of claim:

v_{p} (n!) = \sum_{r = 1}^{\infty} ⌊ \frac{n}{p^{r}} ⌋ < \sum_{r = 1}^{\infty} \frac{n}{p^{r}} = \frac{n \cdot \frac{1}{p}}{1 - \frac{1}{p}} = \frac{n}{p - 1} .

Therefore

\begin{array}{l} (p - 1) v_{p} (n!) & < n \\ (p - 1) v_{p} (n!) & \leq n - 1 \end{array}

(we go from $<$ to $\leq ∙ - 1$ by noting that the LHS is in $ℤ$ ).

This proves the claim.

Now

\begin{array}{l} v (\frac{b_{n} x^{n}}{n!}) & \geq n r - e (\frac{n - 1}{p - 1}) \\ = (n - 1) \underset{> 0}{\underset{⏟}{(r - \frac{e}{p - 1})}} + r \end{array}

This is always $\geq r$ and $\to \infty$ as $n \to \infty$ . Therefore $\exp (x)$ converges to an element in $π^{r} O_{K}$ .

Same method works for $\log$ . □

Lemma 9.3. $\frac{F (π^{r} O_{K})}{F (π^{r + 1} O_{K})} ≅$ $(k, +)$ for all $r \geq 1$ .

Proof. Definition of formal group gives

F (X, Y) = X + Y + X Y (\dots) .

So if $x, y \in O_{K}$ ,

F (π^{r} x, π^{r} y) \equiv π^{r} (x + y) (m o d π^{r + 1}) .

Therefore

\begin{array}{l} F (π^{r} O_{K}) & \to (k, +) \\ π^{r} x & \mapsto x mod π \end{array}

is a surjective group homomorphism with kernel $F (π^{r + 1} O_{K})$ . □

Corollary. Assuming that:

$| k | < \infty$

Then

F (π O_{K})

has a subgroup of finite index isomorphic to

(O_{K}, +)

Notation. Reduction modulo $π$

\begin{array}{l} O_{K} & \to \frac{O_{K}}{π O_{K}} = k \\ x & \mapsto \tilde{x} \end{array}

Proposition 9.4. Assuming that:

$E ∕ K$ be an elliptic curve

Then the reduction mod

π

of any two minimal Weierstrass equations for

E

define isomorphic curves over

k

Proof. Say Weierstrass equations are related by $[u; r, s, t]$ , $u \in K^{*}$ , $r, s, t \in K$ . Then $Δ_{1} = u^{12} Δ_{2}$ . Both equations minimal gives us that $v (Δ_{1}) = v (Δ_{2})$ , hence $u \in O_{K}^{*}$ .

Transformation formula for the $a_{i}$ and $b_{i} + O_{K}$ is integrally closed, hence $r, s, t \in O_{K}$ .

The Weierstrass equations obtained by reducing mod $π$ are now related by $[ũ; \tilde{r}, \tilde{s}, \tilde{t}]$ , $ũ \in k^{*}$ , $\tilde{r}, \tilde{s}, \tilde{t} \in k$ . □

Definition. The reduction $Ẽ ∕ k$ of $E ∕ K$ is defined by the reduction of a minimal Weierstrass equation.

$E$ has good reduction if $Ẽ$ is non-singular (and so an elliptic curve) otherwise has bad reduction.

For an integral Weierstrass equation,

If $v (Δ) = 0$ then good reduction.
If $0 < v (Δ) < 12$ then bad reduction.
If $v (Δ) \geq 12$ then beware that the equation might not be minimal.

There is a well-defined map

\begin{array}{l} ℙ^{2} (K) & \to ℙ^{2} (k) \\ (x : y : z) & \mapsto (\tilde{x} : ỹ : \tilde{z}) \end{array}

(choose a representative with $\min (v (x), v (y), v (z)) = 0$ ).

We restrict to give

\begin{array}{l} E (K) & \to Ẽ (K) \\ P & \mapsto \tilde{P} \end{array}

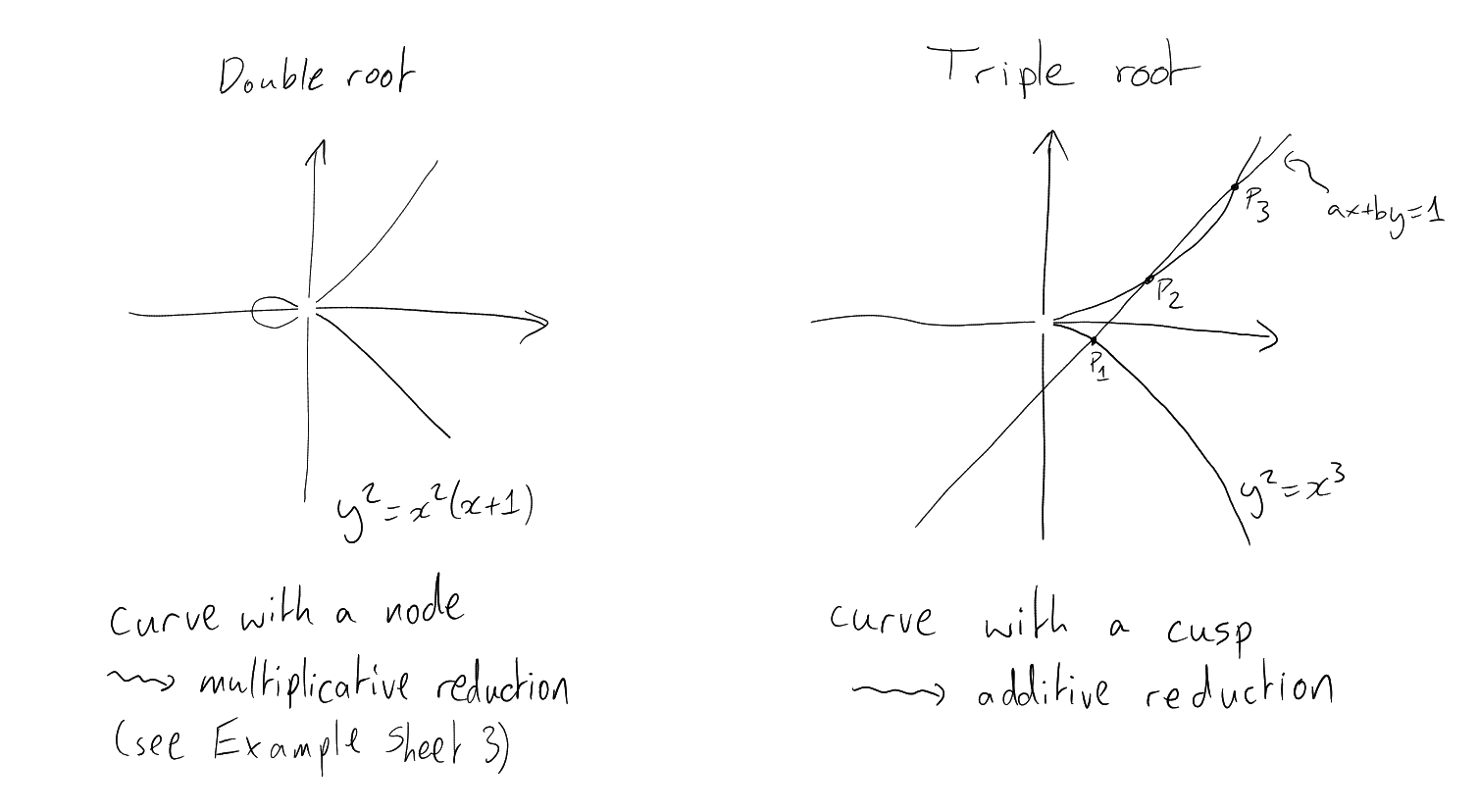
If $P = (x, y) \in E (K)$ then by Lemma 9.1 either

$x, y \in O_{K}$ in which case $\tilde{P} = (\tilde{x}, ỹ)$ .
or $v (x) = - 2 s$ , $v (y) = - 3 s$ for some $s \geq 1$ , in which case $P = (x : y : 1) = (π^{3 s} x : π^{3 s} y : π^{3 s})$ and $\tilde{P} = (0 : 1 : 0)$ .

Therefore

E_{1} (K) = I d i d n^{'} t m a n a g e t o w r i t e t h i s b e f o r e i t w a s r u b b e d o f f

“kernel of reduction”.

Notation.

{\begin{matrix} Ẽ & if E has good reduction \\ Ẽ ∖ {singular point} & if E has bad reduction \end{matrix}

The chord and tangent process still defines a group law on $Ẽ_{ns}$ .

In cases of bad reduction, $Ẽ_{ns} ≅ 𝔾_{m}$ (over $k$ or possibly a quadratic extension of $k$ ) or $Ẽ_{ns} ≅ 𝔾_{a}$ (over $k$ ).

For simplicity we suppose $char k \neq 2$ .

Then $Ẽ = y^{2} = f (x)$ , $\deg f = 3$ .

\begin{array}{l} Ẽ_{ns} & \to_{}^{≅} 𝔾_{a} \\ (x, y) & \mapsto \frac{x}{y} \\ (t^{- 2}, t^{- 3}) & \leftarrow ↤ t \\ (point at \infty) & \leftarrow ↤ 0 \end{array}

Let

P_{1}, P_{2}, P_{3}

lie on the line

a x + b y = 1

. Write

P_{i} = (x_{i}, y_{i})

t_{i} = \frac{x_{i}}{y_{i}}

. Then

x_{i}^{3} = y_{i}^{2} = y_{i}^{2} (a x_{i} + b y_{i})

. So

t_{i}^{3} - a t_{i} - b = 0

. So

t_{1}, t_{2}, t_{3}

are the roots of

T^{3} - a T - b = 0

Looking at coefficient of $T^{2}$ gives $t_{1} + t_{2} + t_{3} = 0$ .

Definition ( $E_{0} (K)$ ). $E_{0} (K) = {P \in E (K) | \tilde{P} \in Ẽ_{ns} (k)}$ .

Proposition 9.5. $E_{0} (K)$ is a subgroup of $E (K)$ and reduction modulo $π$ is a surjective group homomorphism $E_{0} (K) \to Ẽ_{ns} (k)$ .

Note. If $E ∕ K$ has good reduction, then this is a surjective group homomorphism $E (K) \to Ẽ (k)$ .

Proof. Group homomorphism: A line $l$ in $ℙ^{2}$ defined over $K$ has equation

l : a X + b Y + c Z = 0 a, b, c \in K .

We may assume $\min (v (a), v (b), v (c)) = 0$ . Reduction modulo $π$ gives a line

\tilde{l} : ã X + \tilde{b} Y + \tilde{c} Z = 0 .

If $P_{1}, P_{2}, P_{3} \in E (K)$ with $P_{1} + P_{2} + P_{3} = 0$ then these points lie on a line $l$ . So ${\tilde{P}}_{1}, {\tilde{P}}_{2}, {\tilde{P}}_{3}$ lie on the line $\tilde{l}$ . If ${\tilde{P}}_{1}, {\tilde{P}}_{2} \in {\tilde{(}}_{ns} k)$ then ${\tilde{P}}_{3} \in {\tilde{(}}_{ns} k)$ .

So if $P_{1}, P_{2} \in E_{0} (K)$ then $P_{3} \in E_{0} (K)$ and ${\tilde{P}}_{1} + {\tilde{P}}_{2} + {\tilde{P}}_{3} = 0$ .

[Exercise: check this still works if $# {{\tilde{P}}_{1}, {\tilde{P}}_{2}, {\tilde{P}}_{3}} < \infty$ ]

Surjective: Let $f (x, y) = y^{2} + a_{1} x y + a_{3} y - (x^{3} + \dots)$ . Let $\tilde{P} \in Ẽ_{ns} (k) ∖ {0}$ , say $\tilde{P} = ({\tilde{x}}_{0}, ỹ_{0})$ for some $x_{0}, y_{0} \in O_{K}$ .

Since $\tilde{P}$ non-singular, either:

(i) $\frac{\partial f}{\partial x} (x_{0}, y_{0}) ⁄ \equiv 0 (m o d π)$ .
(ii) $\frac{\partial f}{\partial y} (x_{0}, y_{0}) ⁄ \equiv 0 (m o d π)$ .

If (i) then put $g (t) = f (t, y_{0}) \in O_{K} [t]$ . Then

{\begin{matrix} g (x_{0}) \equiv 0 & (m o d π) \\ g^{'} (x_{0}) \in O_{K}^{*} \end{matrix}

Hensel’s lemma gives us that there exists $b \in O_{K}$ such that

{\begin{matrix} g (b) = 0 \\ b \equiv x_{0} (m o d π) \end{matrix}

Then $(b, y_{0}) \in E (K)$ has erduction $\tilde{P}$ . asdfadsf □

Recall that for $r \geq 1$ we put

E_{r} (K) = {(x, y) | v (x) \leq - 2 r, v (y) \leq - 3 r} \cup {0} .

If $r > \frac{e}{p - 1}$ , these give:

\underset{≅ (O_{K}, +)}{\underset{⏟}{E_{r} (K)}} \subset \dots \subset \underset{= Ê (π^{2} O_{K})}{\underset{⏟}{E_{2} (K)}} \subset \underset{= Ê (π O_{K})}{\underset{⏟}{E_{1} (K)}} \subset E_{0} (K) \subset E (K),

where for $i \geq 1$ , each $E_{i + 1} (K) \subset E_{i} (K)$ gives a quotient isomorphic to $(k, +)$ .

We have $\frac{E_{0} (K)}{E_{1} (K)} ≅ Ẽ_{ns} (k)$ .

What about $\frac{E (K)}{E_{0} (K)}$ ?

Lemma 9.6. Assuming that:

$| k | < \infty$

Then

E_{0} (K) \subset E (K)

has finite index.

Proof. $| k | < \infty$ implies that $\frac{O_{K}}{π^{r} O_{K}}$ is finite for all $r \geq 1$ .

Hence

O_{K} ≅ \lim_{\overset{[}{r}] \leftarrow} \frac{O_{K}}{π^{r} O_{K}}

is a profinite group, hence compact.

Then $ℙ^{n} (K)$ is the union of sets

{(a_{0} : \dots : a_{i - 1} : 1 : a_{i + 1} : \dots : a_{n}) : a_{j} \in O_{K}}

and hence compact (for the $π$ -adic topology).

Now note $E (K) \subset ℙ^{2} (K)$ is a closed subset, hence compact.

So $E (K)$ is a compact topological group.

If $Ẽ$ has a singular point $({\tilde{x}}_{0}, ỹ_{0})$ then

E (K) ∖ E_{0} (K) = {(x, y) \in E (K) | v (x - x_{0}) \geq 1, v (y - y_{0}) \geq 1}

is a closed subset of $E (K)$ hence $E_{0} (K)$ is an open subgroup of $E (K)$ .

The cosets of $E_{0} (K)$ are an open cover of $E (K)$ . Hence $[E (K) : E_{0} (K)] < \infty$ . □

Definition (Tamagawa number). $c_{K} (E) = [E (K) : E_{0} (K)]$ is called the Tamagawa number.

Remark.

(i) If we have good reduction then $c_{K} (E) = 1$ (converse is false).
(ii) It can be shown that
- either $c_{K} (E) = v (Δ)$
- or $c_{K} (E) \leq 4$
for the above statements: it is essential that we work with minimal Weierstrass equations.

We deduce:

Theorem 9.7. Assuming that:

$[K : ℚ_{p}] < \infty$

Then

E (K)

contains a subgroup of finite index isomorphic to

(O_{K}, +)

Let $[K : ℚ_{p}] < \infty$ and $L ∕ K$ a finite extension. Let the residue fields be $k^{'}$ and $k$ , and let $f = [k^{'} : k]$ .

Facts:

(i) $[L : K] = e f$ .
(ii) If $L ∕ K$ is Galois then the natural map $Gal (L ∕ K) \to Gal (k^{'} ∕ k)$ is surjective with kernel of order $e$ .

Definition (Unramified). $L ∕ K$ is unramified if $e = 1$ .

Fact: For each $m \geq 1$

(i) $k$ has a unique extension of degree $m$ (say $k_{m}$ ).
(ii) $K$ has a unique unramified extension of degree $m$ (say $K_{m}$ ).

These extensions are Galois, with cyclic Galois groups.

Definition (Maximal unramified extension). $K^{nr} = ⋃_{m \geq 1} K_{m}$ (inside $\bar{K}$ ). “maximal unramified extension”

Theorem 9.8. Assuming that:

$[K : ℚ_{p}] < \infty$
$E ∕ K$ has good reduction
$p ∤ n$
$P \in E (K)$

Then

K ({[n]}^{- 1} P) ∕ K

is unramified.

Notation.

{[n]}^{- 1} (P) = {Q \in E (\bar{K}) : n Q = P},

K ({Q_{1}, \dots, Q_{r}}) = K (x_{1}, \dots, x_{r}, y_{1}, \dots, y_{r}),

where $Q_{i} = (x_{i}, y_{i})$ .

Proof. For each $m \geq 1$ there is a short exact sequence

0 \to E_{1} (K_{m}) \to E (K_{m}) \to Ẽ (K_{m}) \to 0 .

Taking $⋃_{m \geq 1}$ gives a commutative diagram with exact rows:

--
0 E1(Knr) E (Knr) ˜E(k) 0

0 E1(Knr) E (Knr) ˜E(k) 0

An isomorphism by Corollary 8.5 applied over each $K_{m}$ (using $p ∤ n$ here).

surjective by Theorem 2.8
kernel $≅ {(ℤ ∕ n ℤ)}^{2}$ by Theorem 6.5 (again using $p ∤ n$ ).

Snake lemma gives

{\begin{matrix} E (K^{nr}) [n] ≅ {(ℤ ∕ n ℤ)}^{2} \\ \frac{E (K^{nr})}{n E (K^{nr})} = 0 \end{matrix}

So if $P \in E (K)$ then there exists $Q \in E (K^{nr})$ such that $n Q = P$ and

{[n]}^{- 1} P = {Q + T : T \in E [n]} \subset E (K^{nr}) .

Hence $K ({[n]}^{- 1} P) \subset K^{nr}$ and so $K ({[n]}^{- 1} P) ∕ K$ is unramified. □