The Riemann Zeta Function - Analytic Number Theory

3 The Riemann Zeta Function

Recall that the Riemann zeta function is defined by

ζ (s) = \sum_{n = 1}^{\infty} \frac{1}{n^{s}}

for $Re (s) > 1$ .

Remarkable properties:

(1) $ζ (s)$ extends meromorphically to $ℂ$ .
(2) A functional equation relating $ζ (s) \leftrightarrow ζ (1 - s)$ .
(3) All the (non-trivial) zeroes appear to be on the line $Re (s) = \frac{1}{2}$ (Riemann hypothesis).
(4) $ζ (s)$ closely relates to the distribution of primes.

Notation. $f (x) ≍ g (x)$ means $f (x) ≪ g (x) ≪ f (x)$ . $≍_{σ}$ means that the constant in $≪$ can depend on $σ$ .

Lemma 3.1. Assuming that:

$σ > 1$
$t \in ℝ$

Then

| ζ (σ + i t) | ≍_{σ} 1

Proof. By the Euler product formula,

ζ (σ + i t) = \prod_{p} {(1 - p^{- σ - i t})}^{- 1},

hence

| ζ (σ + i t) | = \prod_{p} | 1 - p^{- σ - i t} |^{- 1} .

By the triangle inequality,

1 - p^{- σ} \leq | 1 - p^{- σ - i t} | \leq 1 + | p^{- σ - i t} | = 1 + p^{- σ} .

Hence,

\prod_{p} {(1 - p^{- σ})}^{- 1} \geq | ζ (σ + i t) | \geq \prod_{p} {(1 = p^{- σ})}^{- 1} .

Note that these products converge if and only if $\sum_{p} p^{- σ}$ converges, and this sum converges by the comparison test. □

Lemma 3.2 (Polynomial growth of $e t a$ in half-planes).

(i)
$f (ζ)$ extends to a meromorphic function on $ℂ$ , with the only pole being a simple pole which is at $s = 1$ .
(ii)
Let $k \geq 0$ be an integer. Then, for $Re (s) \geq - k$ and $| s - 1 | \geq \frac{1}{10}$ we have $| ζ (s) | ≪_{k} | s |^{k + 2} + 1$ .

Proof. Let $k \geq 0$ be an integer.

We claim that there exist polynomials $P_{k}$ , $Q_{k}$ of degree $\leq k + 1$ and such that for $Re (s) > 1$ ,

ζ (s) = \frac{1}{s - 1} + Q_{k} (s) + s (s + 1) \dots (s + k) \int_{1}^{\infty} \frac{P_{k} ({t})}{t^{s + k + 1}} d t . (∗)

First assume ( $*$ ) holds.

Then, since $P_{k} ({t}) ≪_{k} 1$ , for $Re (s) > - k - \frac{1}{2}$ , $| s - 1 | \geq \frac{1}{10}$ , ( $*$ ) gives $| ζ (s) | ≪_{k} | s |^{k + 2} + 1$ . So (ii) follows.

For (i), using analytic continuation and ( $*$ ), it suffices to show that the RHS of ( $*$ ) is meromorphic for $Re (s) > - k$ , with the only pole a simple one at $s = 1$ .

Suffices to show that

\int_{1}^{\infty} \frac{P_{k} ({t})}{t^{s + k + 1}} d t

is analytic for $Re (s) > - k$ .

This follows from the following criterion: If $U \subseteq ℂ$ is open, $f : U \times ℝ \to ℂ$ is piecewise continuous, and if $s \mapsto f (s, t)$ is analytic in $U$ for any $t \in ℝ$ , then $\int_{ℝ} f (s, t) d t$ is analytic in $U$ , provided that $\int_{ℝ} | f (s, t) | d t$ is bounded on compact subsets of $U$ .

Applying this with $f (s, t) = \frac{P_{k} ({t})}{t^{s + k + 1}} 𝟙_{[1, \infty)}$ concludes the proof of (i) assuming ( $*$ ).

We are left with proving ( $*$ ). We use induction on $k$ .

Case $k = 0$ : By Partial Summation,

\begin{array}{l} ζ (s) & = \sum_{n = 1}^{\infty} \frac{1}{n^{s}} \\ = s \int_{1}^{\infty} \frac{⌊ u ⌋}{u^{s + 1}} d u & (apply partial summation to \sum_{n \leq x} n^{- s} and let x \to \infty) \\ = s \int_{1}^{\infty} \frac{1}{u^{s}} d u - \int_{1}^{\infty} \frac{{u}}{u^{s + 1}} d u \\ = \frac{1}{s - 1} + 1 - s \int_{1}^{\infty} \frac{{u}}{u^{s + 1}} d u \end{array}

Take $P_{0} (u) = u$ , $Q_{0} (u) = 1$ .

Case $k + 1$ assuming $k$ : Let

c_{k} = \int_{0}^{1} P_{k} ({t}) d t .

For $Re (s) > 1$ , we have

ζ (s) = \frac{1}{s - 1} + Q_{k} (s) + c_{k} s (s + 1) \dots (s + k - 1) + s (s + 1) \dots (s + k) \int_{1}^{\infty} \frac{P_{k} ({t}) - c_{k}}{t^{s + k + 1}} d t .

Let

P_{k + 1} (u) = - \int_{0}^{u} (P_{k} (t) - c_{k}) d t .

This is a polynomial of degree $\leq k + 2$ . By integration by parts,

\int_{1}^{\infty} \frac{P_{t} ({t}) - c_{k}}{t^{s + k + 1}} d t = (s + k + 1) \int_{1}^{\infty} \frac{P_{k + 1} ({u})}{u^{s + k + 1}} d u .

Substituting this into the previous equation, we get that case $k + 1$ follows. □

The Gamma function

Definition (Gamma function). For $Re (s) > 0$ , let

Γ (s) = \int_{0}^{\infty} t^{s - 1} e^{- t} d t .

Lemma 3.3. $Γ (s)$ is analytic for $Re (s) > 0$ .

Proof. Apply the same criterion for integral of analytic function being analytic as in the previous lemma, taking $f (s, t) = t^{s - 1} e^{- t} 𝟙_{[0, \infty)} (t)$ .

Note that for $0 < σ_{1} \leq Re (s) \leq σ_{2}$ ,

\int_{ℝ} | f (s, t) | d t \leq \int_{0}^{1} t^{σ_{1} - 1} e^{- t} d t + \int_{1}^{\infty} t^{σ_{2} - 1} e^{- t} d t < \infty . □

Lemma (Functional equation for $Γ$ ). The $Γ$ function extends meromorphically to $ℂ$ , with the only poles being simple poles at $s = 0, - 1, - 2, \dots$ .

Moreover:

(i) $Γ (s + 1) = s Γ (s)$ for $s \in ℂ$ .
(ii) $Γ (s) Γ (1 - s) = \frac{π}{\sin (π s)}$ for all $s \in ℂ$ (Euler reflection formula).

Proof.

(i) For $Re (s) > 0$ , by integration by parts,
$\int_{0}^{\infty} t^{s} e^{- t} d t = s \int_{0}^{\infty} t^{s - 1} e^{- t} d t .$

This proves (i) for $Re (s) > 0$ .

Now for any $k \in ℕ$ , for $Re (s) > 0$ we have
$Γ (s) = \frac{Γ (s + k)}{(s + k - 1) \dots (s + 1) s} .$

The RHS is analytic for $Re (s) > - k$ , so can use analytic continuation to extend $Γ (s)$ meromorphically to $Re (s) > - k$ , with the only poles being simple poles at $s = 0, - 1, \dots, - k, - 1$ .

Let $k \to \infty$ .
(ii) Since both sides are analytic in $ℂ ∖ ℤ$ , by analytic continuation, it suffices to prove the formula for $0 < s < 1$ .
Now, for any $t > 0$ ,
$\begin{array}{l} t^{s - 1} Γ (s - 1) & = t^{s - 1} \int_{0}^{\infty} u^{- s} e^{- u} d u \\ = \int_{0}^{\infty} v^{- s} e^{- v t} d t & (u = v t) \end{array}$
Multiply by $e^{- t}$ and integrate, and use Fubini to get
$\begin{array}{l} Γ (s) Γ (s - 1) & = \int_{0}^{\infty} \int_{0}^{\infty} v^{- s} e^{- v t} d v e^{- t} d t \\ = \int_{0}^{\infty} \int_{0}^{\infty} e^{- (v + 1) t} d t v^{- s} d v \\ = \int_{0}^{\infty} \frac{v^{- s}}{1 + v} d v \\ = \int_{- \infty}^{\infty} \frac{e^{(1 - s) x}}{1 + e^{x}} d x & (v = e^{x}) \end{array}$
Hence, the remaining task is to show
$\int_{- \infty}^{\infty} \frac{e^{(1 - s) x}}{1 + e^{x}} d x = \frac{π}{\sin (π s)} .$

We will do this next time.

□

Theorem 3.4 (Functional equation for $z e t a$ ). Assuming that:

$ξ (s) = \frac{1}{2} s (s - 1) π^{- s ∕ 2} Γ (\frac{s}{s}) ζ (s)$ for $s \in ℂ$

Then

ξ

is an entire function and

ξ (s) = ξ (1 - s)

for

s \in ℂ

. Hence

π^{- s ∕ 2} Γ (\frac{s}{2}) ζ (s) = π^{- \frac{1 - s}{2}} Γ (\frac{1 - s}{2}) ζ (1 - s)

for $s \in ℂ ∖ {0, 1}$ .

Proof. Let $Re (s) > 1$ . Then,

Γ (\frac{s}{2}) = \int_{0}^{\infty} t^{\frac{s}{2} - 1} e^{- t} d t .

Make the change of variables $f = π n^{2} u$ to get

Γ (\frac{s}{2}) = π^{s ∕ 2} n^{s} \int_{0}^{\infty} u^{\frac{s}{2} - 1} e^{- π n^{2} u} d u .

Hence

π^{- \frac{s}{2}} n^{- s} Γ (\frac{s}{2}) = \int_{0}^{\infty} u^{\frac{s}{2} - 1} e^{- π n^{2} u} d u .

Summing over $n \in ℕ$ and using Fubini,

\begin{array}{l} π^{- \frac{s}{2}} Γ (\frac{s}{2}) ζ (s) & = \sum_{n = 1}^{\infty} \int_{0}^{\infty} u^{\frac{s}{2} - 1} e^{- π n^{2} u} d u \\ = \frac{1}{2} \int_{0}^{\infty} u^{\frac{s}{2} - 1} (𝜃 (u) - 1) d u & 𝜃 (u) = \sum_{n = - \infty}^{\infty} e^{- π n^{2} u} \\ = \frac{1}{2} \int_{0}^{1} u^{\frac{s}{2} - 1} (𝜃 (u) - 1) d u + \frac{1}{2} \int_{1}^{\infty} u^{\frac{s}{2} - 1} (𝜃 (u) - 1) d u & (*) \end{array}

By the functional equation

𝜃 (u) = \frac{1}{\sqrt{u}} 𝜃 (\frac{1}{u}),

we have

\begin{array}{l} \int_{0}^{1} u^{\frac{s}{2} - 1} (𝜃 (u) - 1) d u & = \int_{0}^{1} u^{\frac{s}{2} - \frac{3}{2}} 𝜃 (\frac{1}{u}) d u - \int_{0}^{1} u^{\frac{s}{2} - 1} d u \\ = \int_{1}^{\infty} v^{- \frac{s + 1}{2}} 𝜃 (v) d v - \int_{0}^{1} u^{\frac{s}{2} - 1} d u & (u = \frac{1}{v}) \\ = \int_{1}^{\infty} v^{- \frac{s + 1}{2}} (𝜃 (v) - 1) d v + \underset{\frac{1}{\frac{s - 1}{2}}}{\underset{⏟}{\int_{1}^{\infty} v^{- \frac{s + 1}{2}} d v}} - \underset{\frac{1}{\frac{s}{2}}}{\underset{⏟}{\int_{0}^{1} u^{\frac{s}{2} - 1} d u}} \end{array}

Plugging this into ( $*$ ), we get

π^{- \frac{s}{2}} Γ (\frac{s}{2}) ζ (s) = \frac{1}{2} \int_{1}^{\infty} (u^{- \frac{s + 1}{2}} + u^{\frac{s}{2} - 1}) (𝜃 (u) - 1) d u - \frac{1}{s (s - 1)} .

Hence

ξ (s) = - \frac{1}{2} + \frac{1}{4} s (s - 1) \int_{1}^{\infty} (u^{- \frac{s + 1}{2}} + u^{\frac{s}{2} - 1}) (𝜃 (u) - 1) d u . (∗∗)

Since $| 𝜃 (u) - 1 | ≪ e^{- π u}$ , applying the criterion for integrals of analytic functions being analytic, we see that $ξ (s)$ is entire. So by analytic continuation, ( $* *$ ) holds for all $s \in ℂ$ .

Moreover, the expression for $ζ (s)$ is symmetric with respect to $s \mapsto 1 - s$ , so $ξ (s) = ξ (1 - s)$ , $s \in ℂ$ . □

Corollary 3.5 (Zeroes and poles of $z e t a$ ). The $ζ$ function extends to a meromorphic function in $ℂ$ and it has

(i)
Only one pole, which is a simple pole at $s = 1$ , residue $1$ .
(ii)
Simple zeroes at $s = - 2, - 4, - 6, \dots$ .
(iii)
Any other zeroes satisfy $0 \leq Re (s) \leq 1$ .

Proof.

(ii) – (iii) Follows from the lemma on polynomial growth of $ζ$ on vertical lines.
(ii) – (iii) We know $ζ (s) \neq 0$ for $Re (s) > 1$ . We want to show that if $ζ (s) = 0$ and $Re (s) > 0$ then $s \in {- 2, - 4, - 6, \dots}$ and $s$ is a simple zero.
Let $Re (s) > 0$ . By the functional equation for $ζ$ ,

$ζ (s) = \underset{\neq 0}{\underset{⏟}{π^{s - \frac{1}{2}}}} \frac{Γ (\frac{1 - s}{2})}{Γ (\frac{s}{2})} ζ (1 - s) .$

We claim that $Γ (s) \neq 0$ for all $s \in ℂ$ . By the Euler reflection formula,
$Γ (s) Γ (1 - s) \sin (π s) = π,$

for $s \in ℂ$ .

If $Γ (s) = 0$ , then $Γ$ has a pole at $1 - s$ . Hence, $1 - s = - n$ for some $n \geq 0$ integer. But then $s = n + 1$ , and $Γ (n + 1) = n! \neq 0$ .

We conclude that for $Re (s) < 0$ ,
$\begin{array}{l} ζ (s) = 0 & ⟺ \frac{s}{2} is a pole of Γ \\ ⟺ s = - 2 n, n \in ℕ \end{array}$
Since the poles of $Γ$ are simple, $ζ$ has a simple zero at $s = - 2 n$ , $n \in ℕ$ . □

3.1 Partial fraction approximation of $ζ$

This is a formula for $\frac{ζ^{'} (s)}{ζ (s)}$ .

For the proof we need a lemma. We write, for $z \in ℂ$ , $r > 0$ ,

\begin{array}{l} B (z_{0}, r) & = {z \in ℂ : | z - z_{0} | < r} \\ \bar{B (z_{0}, r)} & = {z \in ℂ : | z - z_{0} | \leq r} \\ \partial B (z_{0}, r) & = {z \in ℂ : | z - z_{0} | = r} \end{array}

Lemma 3.6 (Borel-Caratheodory Theorem). Assuming that:

$0 < r < R$
$f$ analytic in $\bar{B (0, R)}$ , with $f (0) = 0$

Then

\sup_{| z | \leq r} | f (z) | \leq \frac{2 r}{R - r} \sup_{| z | = R} Re (f (z)) .

Proof. This is Exercise 10 on Example Sheet 2. □

Lemma 3.7 (Landau). Assuming that:

$z_{0} \in ℂ$ and $r > 0$
$f$ analytic in $B (z_{0}, r)$
for some $M > 1$ we have $| f (z) | < e^{M} | f (z_{0}) |$ for all $z \in B (z_{0}, r)$

Then for

z \in B (z_{0}, r ∕ 4)

| \frac{f^{'} (z)}{f (z)} - \sum_{ρ \in Z} \frac{1}{z - ρ} | \leq \frac{96 M}{r},

where $Z$ is the set of zeroes of $f$ in $\bar{B (z_{0}, r ∕ 2)}$ , counted with multiplicities.

Note. If $f$ is a polynomial, we can factorise

f (z) = a \prod_{ρ} (z - ρ),

and then

\begin{array}{l} \frac{f^{'} (z)}{f (z)} & = {(\log f (z))}^{'} \\ = {(\log a + \sum_{ρ} \log (z - ρ))}^{'} \\ = \sum_{ρ} \frac{1}{z - ρ} \end{array}

Proof. Let

g (z) = \frac{f (z)}{\prod_{ρ \in Z} (z - ρ)} .

Then $g$ is analytic and non-vanishing in $\bar{B (z_{0}, r ∕ 2)}$ . Note that

\frac{g^{'} (z)}{g (z)} = \frac{f^{'} (z)}{f (z)} - \sum_{ρ \in Z} \frac{1}{z - ρ}

( $\frac{{(f_{1} - f_{n})}^{'}}{f_{1} - f_{n}} = \sum_{i = 1}^{n} \frac{f_{1}^{'}}{f_{1}}$ ).

Hence, it suffices to prove

| \frac{g^{'} (z)}{g (z)} | \leq \frac{96 M}{r}

for $z \in B (z_{0}, r ∕ 4)$ . Write

h (z) = \frac{g (z_{0} + z)}{g (z_{0})} .

Then $h$ is analytic and non-vanishing in $\bar{B (0, r ∕ 2)}$ , and $h (0) = 1$ . We want to show

| \frac{h^{'} (z)}{h (z)} | \leq \frac{96 M}{r}

for $z \in B (0, r ∕ 4)$ .

For all $z_{0} \in \partial B (0, r)$ we have

| h (z) | = | \frac{f (z_{0} + z)}{f (z_{0})} \prod_{ρ \in Z} \frac{z_{0} - ρ}{z_{0} + z - ρ} | \leq | \frac{f (z_{0} + z)}{f (z_{0})} | < e^{M}

since

| z_{0} - ρ | \leq \frac{r}{2} = r - \frac{r}{2} \leq | z_{0} + z - ρ |

for $z \in \partial B (0, r)$ .

By the maximum modulus principle, $| h (z) | < e^{M}$ for $z \in \bar{B (0, r ∕ 2)}$ , so

Re \log h (z) = \log | h (z) | < M .

By the Borel-Caratheodory Theorem with radii $\frac{3 r}{8}$ , $\frac{r}{4}$ we have for for $z \in B (0, 3 r ∕ 8)$ ,

| \log h (z) | \leq \frac{2 \frac{r}{4}}{\frac{3 r}{8} - \frac{r}{4}} M = 4 M .

Now, for $z \in B (0, r ∕ 4)$ , Cauchy’s theorem gives us

\begin{array}{l} | \frac{h^{'} (z)}{h (z)} | & = | \frac{1}{2 π i} \int_{\partial B (0, 3 r ∕ 8)} \frac{\log h (w)}{{(z - w)}^{2}} d w | \\ \leq \frac{1}{2 π} \cdot 2 π \frac{3 r}{8} 4 M {(\frac{3 r}{8} - \frac{r}{4})}^{- 2} \\ = \frac{96 M}{r} □ \end{array}

Theorem 3.8 (Partial Fraction approximation of $z e t a^{'} ∕ z e t a$ ).

(i) Let $s = σ + i t$ with $| σ | \leq 10$ , $s \neq 1$ and $ζ (s) \neq 0$ . Then
$\frac{ζ^{'} (s)}{ζ (s)} = - \frac{1}{s - 1} + \sum_{| ρ - s | \leq \frac{1}{10}} \frac{1}{s - ρ} + O (\log (| t | + 2)) .$

where the sum is over the zeroes $ρ$ of $ζ$ counted with multiplicity.
(ii) For any $T \geq 0$ , there are $≪ \log (T + 2)$ many zeroes $ρ$ of $ζ$ (counted with multiplicity) with $| Im (ρ) | \in [T, T + 1]$ .

Proof. We apply Landau with $z_{0} = 2 + i t$ , $r = 50$ , with $f (s) = (s - 1) ζ (s)$ .

By the lemma on polynomial growth of $ζ$ on vertical lines, for $σ + i t \in B (z_{0}, 50)$ , we have

\begin{array}{l} | f (s) | & \leq C (| t | + 52) {(| t + 2)}^{50} \\ \leq C \exp (51 \log (| t | + 52)) \\ ≪ C \exp (51 \log (| t | + 52)) | f (z) | \end{array}

( $| ζ (z + i t) | ≍ 1$ ).

Let $s \in B (z_{0}, \frac{25}{2})$ . Then Landau gives us

\begin{array}{l} \frac{f^{'} (s)}{f (s)} & = \frac{1}{s - 1} + \frac{ζ^{'} (s)}{ζ (s)} \\ = \sum_{| ρ - z_{0} | \leq 2 S} \frac{1}{s - ρ} + O (\log (| t | + 2)) & (*) \end{array}

Since $B (z_{0}, \frac{25}{2})$ contains all the points $s = σ + i t$ with $| σ | \leq 10$ , it suffices to show

\sum_{\begin{array}{c} | ρ - z_{0} | \leq 25 \\ | ρ - s | > \frac{1}{10} \end{array}} \frac{1}{s - ρ} = O (\log (| t | + 2)) . (∗∗)

Substituting $s = z_{0}$ in ( $*$ ), we get

\begin{array}{l} \sum_{| ρ - z_{0} | \leq 25} \frac{1}{z_{0} - ρ} & = O (| \frac{ζ^{'} (z_{0})}{ζ (z_{0})} | + 1 + \log (| t | + 2)) \\ = O (\log (| t | + 2)) \end{array}

since

\begin{array}{l} | \frac{ζ^{'} (2 + i t)}{ζ (2 + i t)} | & = | \sum_{n = 1}^{\infty} Λ (n) n^{- 2 + i t} | \\ \leq \sum_{n = 1}^{\infty} Λ (n) n^{- 2} \\ = - \frac{ζ (2)}{ζ (2)} \end{array}

Taking real parts,

\sum_{| ρ - z_{0} | \leq 25} \frac{2 - Re (ρ)}{| z_{0} - ρ |^{2}} = O (\log (| t | + 2)) .

Since $Re (ρ) \leq 1$ ,

\sum_{| ρ - z_{0} | \leq 25} \frac{1}{| z_{0} - ρ |^{2}} = O (\log (| t | + 2)) .

This proves part (ii). It gives also ( $* *$ ) since the sum there contains $O (\log (| t | + 2))$ zeros. □

3.2 Zero-free region

Proposition 3.9. Assuming that:

$σ > 1$ and $t \in ℝ$

Then

3 \frac{ζ^{'}}{ζ} (σ) + 4 Re (\frac{ζ^{'}}{ζ} (σ + i t)) + Re (\frac{ζ^{'}}{ζ} (σ + 2 i t)) \leq 0 . (∗∗)

Proof. Recall that

\frac{ζ^{'}}{ζ} (s) = - \sum_{n = 1}^{\infty} \frac{Λ (n)}{n^{s}},

where $Λ$ is the von Mangoldt function function, and $Re (s) > 1$ .

Taking linear combinations, the LHS of ( $* *$ ) becomes

- \sum_{n = 1}^{\infty} Λ (n) \frac{3 + 4 Re (n^{i t}) + Re (n^{- 2 i t})}{n^{σ}} = - \sum_{n = 1}^{\infty} Λ (n) \frac{3 + 4 \cos (t \log n) + \cos (2 + \log n)}{n^{σ}}

( $Re (n^{i u}) = \cos (u \log n)$ ).

We are done by the inequality:

3 + 4 \cos α + \cos 2 α = 2 {(1 + \cos α)}^{2} \geq 0

for $α \in ℝ$ . □

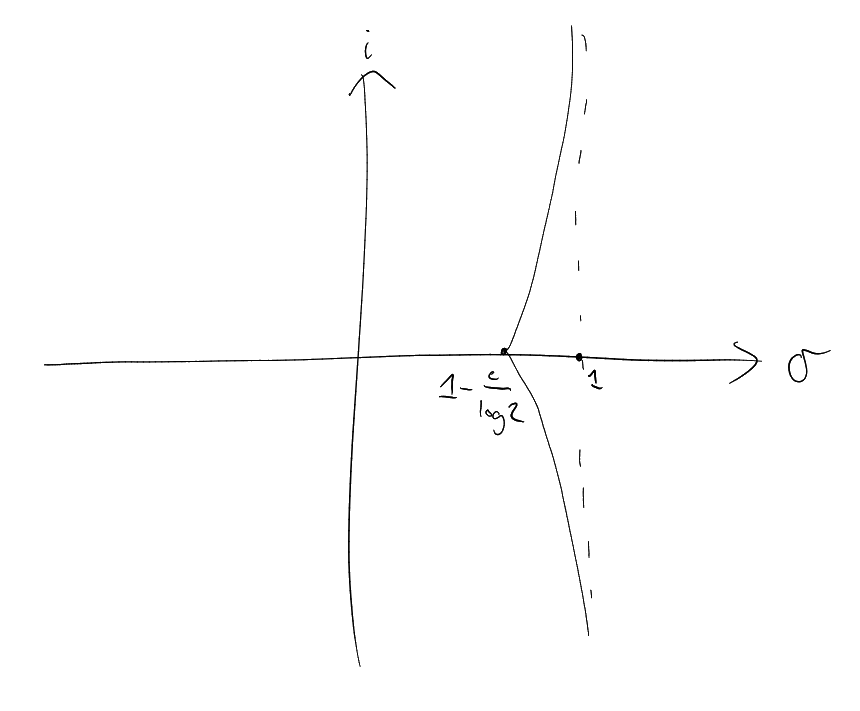
Theorem 3.10 (Zero-free region). There is a constant $c > 0$ such that $ζ (σ + i t) \neq 0$ whenever $σ > 1 - \frac{c}{\log (| t | + 2)}$ . In particular, $ζ (s) \neq 0$ for $Re (s) = 1$ .

Proof. Let $σ \in [1, 2]$ and $t \in ℝ$ . Suppose $ζ (β + i t)$ . uwe know that $β \leq 1$ . We know that $ζ$ has no zeroes in some ball $B (1, r)$ for some $r > 0$ (otherwise the entire function $(s - 1) ζ (s)$ would have an accumulation point for its zeros).

Choosing $c > 0$ small enough, we can assume that $| t | \geq r$ . By the key inequality for $\frac{ζ^{'}}{ζ}$ ,

3 \frac{ζ^{'}}{ζ} (σ) + 4 Re (\frac{ζ^{'}}{ζ} (σ + i t)) . + Re (\frac{ζ^{'}}{ζ} (σ + 2 i t)) . \leq 0 .

Apply partial fraction decomposition of $\frac{ζ^{'}}{ζ}$ . So

\frac{ζ^{'}}{ζ} (s) = - \frac{1}{s - 1} + \sum_{| s - ρ | \leq \frac{1}{10}} \frac{1}{s - ρ} + O (\log (| t | + 2)) . (∗∗)

( $t = Im (s)$ ).

Since $Re (ρ) \leq 1$ for any zero $ρ$ ,

Re \frac{1}{σ + i u - ρ} = \frac{σ - Re (ρ)}{| σ + i u - ρ |^{2}} \geq 0

( $σ > 1$ ).

Discarding terms, we get

- \frac{3}{σ - 1} + \frac{4}{σ - β} \leq C \log (| t | + 2) .

Take $σ = 1 + \frac{s c}{\log (| t | + 2)}$ , and assume $β \geq 1 - \frac{c}{\log (| t | + 2)}$ to get

- 3 \frac{\log (| t | + 2)}{5 c} + 4 \frac{\log (| t | + 2)}{6 c} \leq C (\log | t | + 2) .

Take $c = \frac{1}{16 C}$ to get a contradiction. □

Theorem 3.11 (Bounding $z e t a^{'} ∕ z e t a$ ). Assuming that:

$c > 0$ sufficiently small
$T \geq 0$
$Re (s) \geq - 10$
$| Im (s) | \in [T, T + 1]$
$s$ is at least distance $\frac{c}{\log (T + 2)}$ away from any zero or pole

Then

| \frac{ζ^{'} (s)}{ζ (s)} | ≪_{c} {(\log (T + 2))}^{2} .

Proof. If $s = σ + i t$ with $σ > 10$ , then

\begin{array}{l} | \frac{ζ^{'} (s)}{ζ (s)} | & = | \sum_{n = 1}^{\infty} Λ (n) n^{- s} | \\ \leq \sum_{n = 1}^{\infty} Λ (n) n^{- σ} \\ ≪ 1 \end{array}

Assume then that $Re (s) \in [- 10, 10]$ . Apply ( $* *$ ). Each term satisfies

\begin{array}{l} \frac{1}{| s - ρ |} & \leq \frac{\log (T + 2)}{c} \\ \frac{1}{| s - 1 |} & \leq \frac{\log (T + 2)}{c} \end{array}

We know that there are $O (\log (T + 2))$ zeros with multiplicity having imaginary part $\in [T - 2, T + 2]$ . The claim follows from triangle inequality. □

TODO

3 The Riemann Zeta Function

The Gamma function

3.1 Partial fraction approximation of ζ

3.2 Zero-free region

3.1 Partial fraction approximation of $ζ$