3 Expansion and Cheeger inequality
Assume is
-regular.
Write .
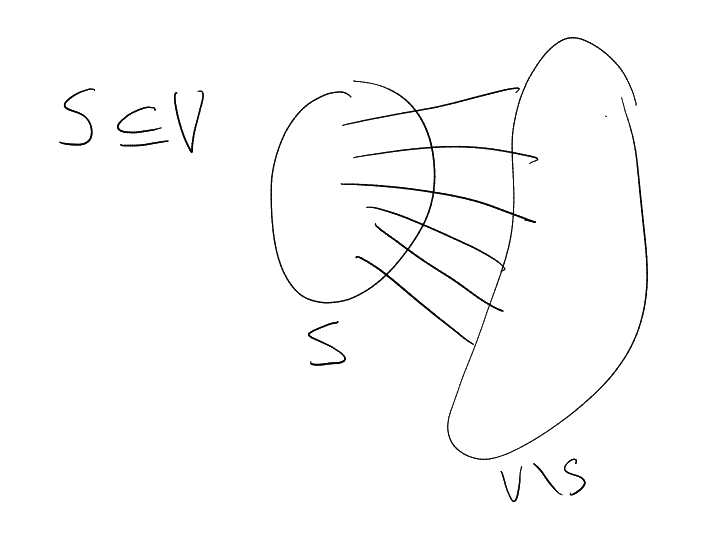
Definition 3.1 (Expansion).
Given a -regular
graph and
, the
expansion of
is
Note that ,
for example because
Definition 3.2 (Edge expansion).
The (edge) expansion of a cut
is
defined as
|
|
Definition 3.3 (Edge expansion of a graph).
The edge expansion of a graph is
|
|
Theorem 3.4 (Cheeger’s inequality).
Assuming that:
Consider 𝟙,
where 𝟙 if
and
𝟙
otherwise. Then
𝟙𝟙𝟙𝟙
Recall
|
|
We pick 𝟙𝟙.
Note
𝟙𝟙𝟙𝟙
Lemma 3.5.
Assuming that:
Then |
|
Proof.
Let ,
such
that
and .
Then
|
|
Then
Proof of left inequality in Cheeger’s inequality.
.
Then minimise over all ,
to get .
□
Recall that
and
|
𝟙 |
Fiedler’s Algorithm
Input: .
-
Sort vertices
such that .
-
Find cut
that minimises .
Output: The cut.
Running time: .
Lemma 3.6.
Assuming that:
If , call a cut
a threshold
cut for .
Lemma 3.7.
Assuming that:
Then there is
such that
,
and any threshold
cut for
is a
threshold cut for
.
Lemma 3.8.
Assuming that:
Then there is
such that
Proof of Lemma 3.7.
If
then
Let be the
median of .
,
. Let
, where
. So
|
|
Note .
Claim: either
or
suffices.
□
Proof of Lemma 3.8.
Assume .
We find . Choose
at random,
such that .
Let
Then
|
|
Have
Also, can calculate:
Then
Now use the following fact to finish:
Fact: If and
are random
variables with ,
then .
(Proof: let .
Then ,
so ,
hence ).
□
Example.
.
This has .
For
with ,
we have . So
|
|
Compare with Cheeger’s inequality:
Example.
,
.
.
We index eigenfunctions by sets .
,
.
.
. If
,
, then
|
|
Harper gives a better bound:
|
|
By considering
being half of the cube, we get
Fiedler’s algorithm: Let ,
.
.
,