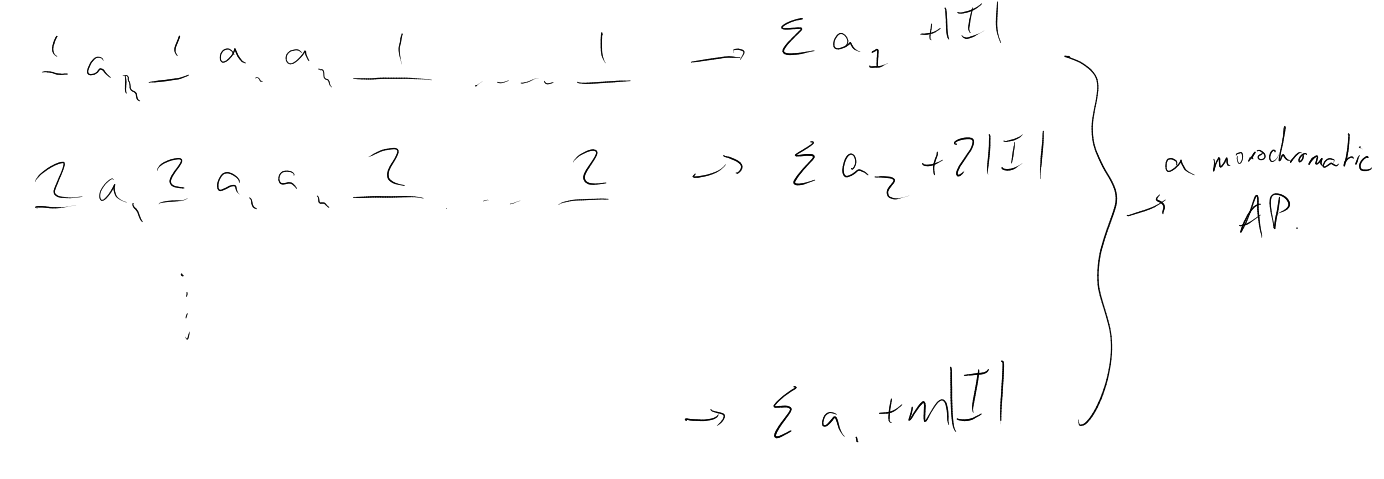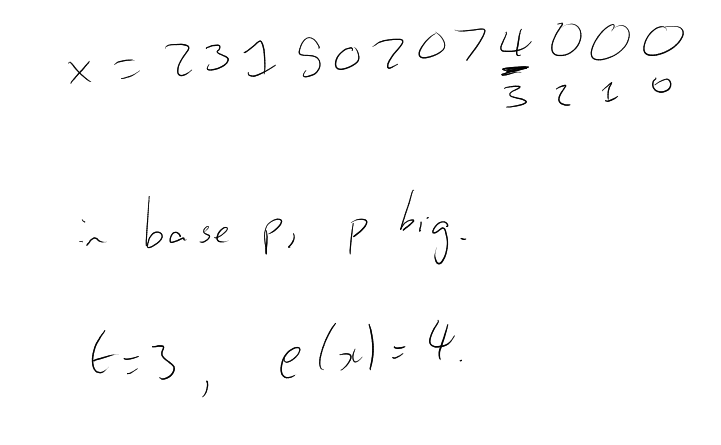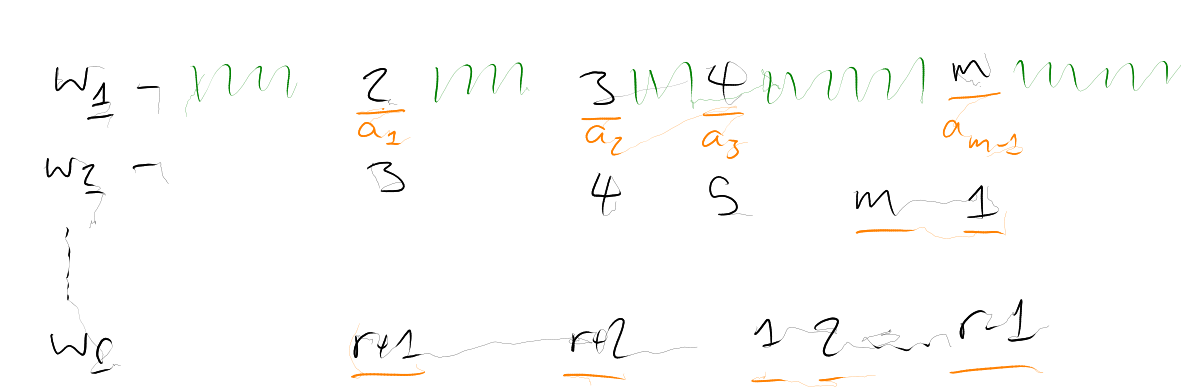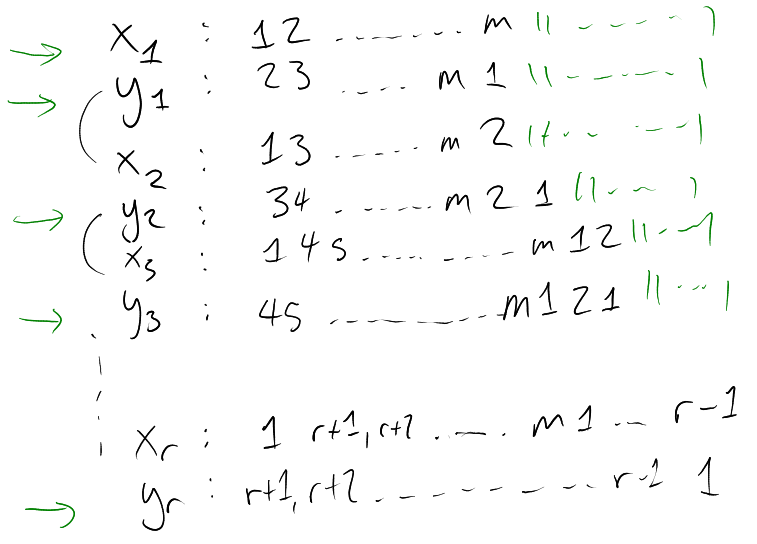Ramsey Theory - Cambridge III notes

Ramsey Theory
Lectured by Maria Ivan

1Ramsey’s Theorem
1.1Van der Waerden’s Theorem
1.2The Hales-Jewett Theorem
2Partition Regular Equations
2.2Ultrafilters
3Euclidean Ramsey
Index

1 Ramsey’s Theorem

Notation. $ℕ = {1, 2, \dots}$ , $[n] = {1, 2, \dots, n}$ for a set $X$ , $r \geq 1$ , $X^{(r)} = {A \subseteq X, | A | = r}$ .

Given a 2-colouring of $ℕ^{(2)}$ , are we guaranteed to have an infinite monochromatic set (i.e. $M \subseteq ℕ$ , $M$ infinite such that the colouring is constant on $M^{(2)}$ )?

Example.

(1) ${i, j}$ red if $i + j$ even, odd otherwise. Then $M = {n : n even}$ works.
(2) ${i, j}$ red if $\max {n : 2^{n} | i + j}$ is even, blue otherwise. Then $M = {4^{0}, 4^{1}, \dots}$ works.
(3) ${i, j}$ red if $i + j$ has an even number of distinct prime divisors, and blue otherwise. No explicit $M$ is known!

Theorem 1.1 (Ramsey’s Theorem for pairs). Assuming that:

$ℕ^{(2)}$ are 2-coloured (i.e. $c : ℕ^{(2)} \to {1, 2}$ ).

Then there exists

M

infinite monochromatic.

Proof. Pick $a_{1} \in ℕ$ . Then there exists an infinite set $A_{1}$ such that $c (a_{1} i) = c_{1}$ for all $i \in A_{1}$ . Pick $a_{2} \in A_{1}$ and find $A_{2}$ (infinite) such that $c (a_{2} i) = c_{2}$ for all $i \in A_{2}$ . Keep on doing this. We end up with $a_{1} < a_{2} < a_{3} < \dots < a_{k} < \dots$ and $A_{1} \supset A_{2} \supset \dots$ such that $c (a_{i} j) = c_{i}$ for all $j \in A_{i}$ .

One colour appears infinitely many times $c_{i_{1}} = c_{i_{2}} = \dots = c_{i_{k}} = \dots = e$ . Now note $M = {a_{i_{1}}, a_{i_{2}}, a_{i_{3}}, \dots}$ is a monochromatic set. □

Remark.

(1) The same proof works for $k$ colours. This is referred to as a “ $2$ -pass” proof. Alternatively: if we have colours $1, 2, \dots, k$ , then we can consider $1$ to be red, and everything else to be blue. Then using the above result and induction, we get an alternative way to prove the theorem for greater than $2$ colours.
(2) Infinite monochromatic is very different than arbitrarily large monochromatic.
For example: suppose we write $A_{1} = {1, 2}$ , $A_{2} = {3, 4, 5}$ , $A_{3} = {6, 7, 8, 9}$ and so on. Say ${i, j}$ is red if there exists $k$ such that $i, j \in A_{k}$ , and blue otherwise. Then there exist arbitrarily large monochromatic red sets, but no infinite monochromatic red set.

What about $ℕ^{(r)}$ with $r = 3$ ?

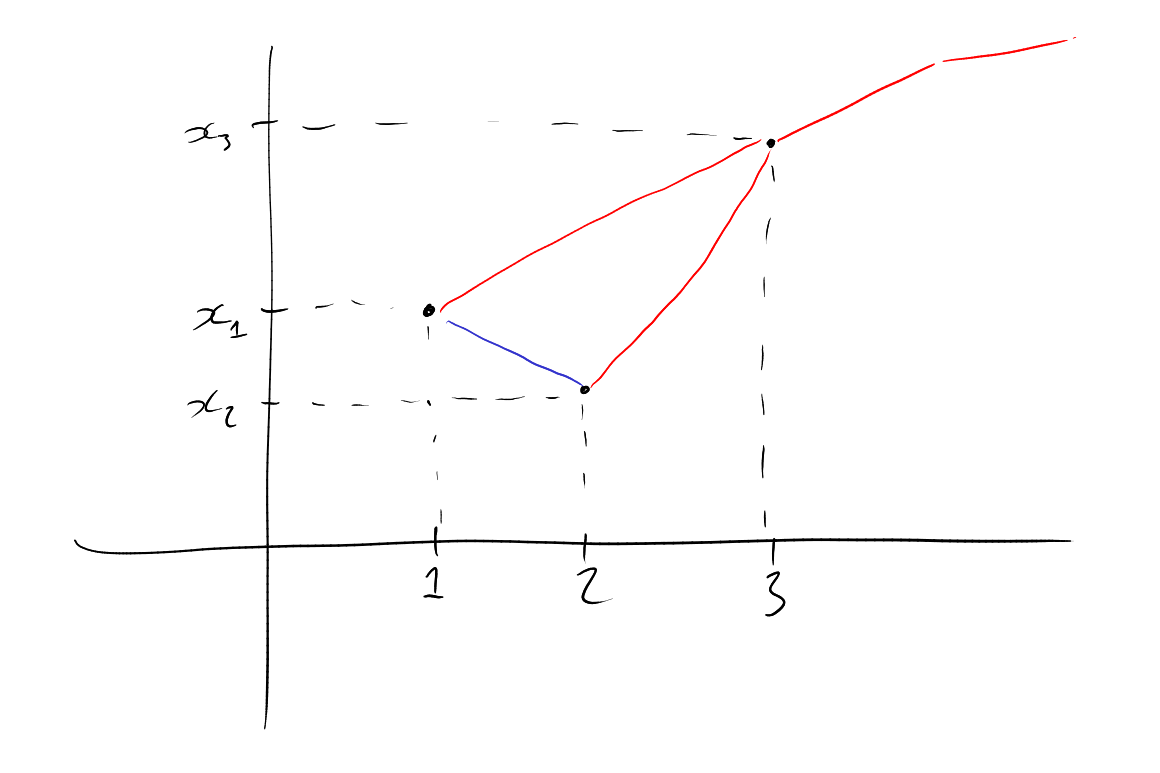
Example. $r = 3$ , ${i, j, k}$ , $i < j < k$ red if and only if $i | j + k$ . Then $M = {2^{0}, 2^{1}, 2^{2}, \dots}$ is monochromatic.

Theorem 1.2 (Ramsey’s Theorem for $r$ -sets). Assuming that:

$ℕ^{(r)}$ is finitely coloured.

Then there exists a monochromatic infinite set.

Proof. $r = 1$ pigeonhole, $r = 2$ is Theorem 1.1. Prove this by induction.

Assume it is true for $r - 1$ . Given $c : ℕ^{(r)} \to [k]$ , we must find $M$ (infinite and monochromatic). Pick $a_{1} \in ℕ$ . Look at the $r - 1$ sets of $ℕ ∖ {a_{1}}$ . Define $c^{'} : {(ℕ ∖ {a_{1}})}^{(r - 1)} \to [k]$ via $c^{'} (F) = c (F \cup {a_{1}})$ .

By induction there exists $A_{1} \subseteq ℕ ∖ {a_{1}}$ such that $c^{'}$ is constant on it, say constantly equal to $c_{1}$ .

Now pick $a_{2} \in A_{1}$ and induce $c^{'} : {(A_{1} ∖ {a_{2}})}^{(r - 1)} \to [k]$ defined by $c^{'} (F) = c (F \cup {a_{2}})$ . By induction there exists $A_{2} \subset A_{1} ∖ {a_{2}}$ such that $c^{'}$ is constant on it, say equal to $c_{2}$ .

Continuing this, we end up with $a_{1}, a_{2}, \dots$ and sets $A_{1}, A_{2}, \dots$ such that $A_{i + 1} \subset A_{i} ∖ {a_{i + 1}}$ with $c (F \cup {a_{i}}) = c_{i}$ for all $F \subset A_{i + 1}$ , $| F | = r - 1$ .

Some colour must appear infinitely many times: say $c_{i_{1}} = c_{i_{2}} = c_{i_{3}} = \dots = c$ . Check: $M = {a_{i_{1}}, a_{i_{2}}, \dots}$ is monochromatic. □

Example. Applications:

(1) In a totally ordered set, any sequence has a monotone subsequence.

Proof. Let the sequence be $x_{1}, x_{2}, \dots$ . Say ${i < j}$ is red if $x_{i} \leq x_{j}$ , and blue otherwise. By Theorem 1.1, we may find $M = {i_{1} < i_{2} < \dots}$ monochromatic. If $M$ is red, then the sequence $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}, \dots$ is increasing, and if $M$ is blue then the sequence is strictly decreasing. □
(2) Using a slightly adjusted argument, we can insist that the function given by $(i_{j}, x_{i_{j}})$ is either concave or convex. We do this by: for a triple $(i_{j_{1}}, i_{j_{2}}, i_{j_{k}})$ we colour it convex or concave. Then apply Theorem 1.2.

From Theorem 1.2 we can deduce:

Theorem 1.3 (Finite Ramsey). Assuming that:

$r \geq 1$ , $k \geq 1$ , $m \geq 1$

Then there exists

n \in ℕ

such that whenever

{[n]}^{(r)}

k

-coloured, we can find a monochromatic set of size

m

Proof. Suppose not. Then for each $n$ we can find $c_{n} : {[n]}^{(r)} \to [k]$ with no monochromatic $m$ -sets. Note that there are only finitely many ways to $k$ -colour ${[r]}^{(r)}$ . So infinitely many $c_{n}$ will agree on ${[r]}^{(r)}$ . Pick $A_{1}$ such that for all $n \in A_{1}$ ,

c_{n} |_{{[r]}^{(r)}} = d r : {[r]}^{(r)} \to [k] .

We can do the same on ${[r + 1]}^{(r)}$ and produce some $A_{2} \subset A_{1}$ such that $c_{n} |_{{[r + 1]}^{(r)}}$ is constant on $A_{2}$ .

Continuing this, we get $\dots \subset A_{n} \subset A_{n - 1} \subset \dots \subset A_{1}$ . They satisfy:

(1) There is no monochromatic $m$ -set for any $d_{n} : {[n]}^{(r)} \to [k]$ (because $d_{n} = c_{i} |_{{[n]}^{(r)}}$ ).
(2) These $d_{n}$ ’s are nested: $d_{j} |_{{[i]}^{(r)}} = d_{i}$ for $j > i$ .

Finally: colour $ℕ^{(r)}$ via $c (F) = d_{n} (F)$ , where $n$ is any integer $n \geq \max F$ . One can see that this is well defined, and gives a contradiction to Theorem 1.2. □

Remark.

(1) This proof gives no bound on this $n (k, m)$ . There are other proofs that give some bounds.
(2) This is a “proof by compactness”: what we (essentially) showed is that ${0, 1}^{ℕ}$ with the product topology is (sequentially) compact. If you prefer, the product topology can be thought of as the topology derived from the metric
$d (f, g) = {\begin{matrix} 0 & f = g \\ \frac{1}{\min {n : f (n) \neq g (n)}} & otherwise \end{matrix} .$

What happens if we have $c : ℕ^{(2)} \to X$ with $X$ being potentially infinite?

Theorem 1.4 (Canonical Ramsey Theorem). Assuming that:

$ℕ^{(2)}$ is coloured (possibly with an infinite number of colours)

Then there exists an infinite set

M

such that one of the following holds:

(i) $c$ is constant on $M$ .
(ii) $c$ is injective on $M$ .
(iii) $c ({i, j}) = c ({k, l})$ if and only if $i = k$ for $i < j$ , $k < l$ in $M$ .
(iv) $c ({i, j}) = c ({k, l})$ if and only if $j = l$ , for all $i < j$ , $k < l$ .

Proof. We colour an element ${i < j < k < l}$ of $ℕ^{(4)}$ as follows: We say that it is red if $c (i j) = c (k l)$ , and blue otherwise.

By Ramsey’s Theorem for $r$ -sets, there exists an infinite set $M_{1}$ that is monochromatic under this colouring.

(1) Suppose $M_{1}$ is red. Then $c$ is constant on $M_{1}$ .
Let $i < j$ , $k < l$ . Pick $m < n$ (in $M_{1}$ ) bigger than all $4$ . Then $i < j < m < n$ hence $c (i j) = c (m n)$ . Also, $k < l < m < n$ , so $c (k l) = c (m n)$ . So $c$ is constant on $M_{1}$ .
(2) Now let’s assume $M_{1}$ is blue. So for $i < j < k < l$ we have $c (i j) \neq c (k l)$ . Next: colour $M_{1}^{(4)}$ as follows: we will say that ${i, j, k, l}$ is green if $c (i l) = c (j k)$ , and purple otherwise. By Ramsey’s Theorem for $r$ -sets we can pick infinite $M_{2} \subset M_{1}$ monochromatic.
We claim that $M_{2}$ cannot be green. This is because if $M_{2}$ is green, let $i < j < k < l < m < n$ in $M_{2}$ . Then:
- ${i < j < k < n}$ gives us that $c (i n) = c (j k)$
- ${i < l < m < n}$ gives us that $c (i n) = c (l m)$
But using these we get $c (j k) = c (l m)$ , which contradicts the fact that ${j < k < l < m}$ is blue.

Therefore $M_{2}$ is purple: for $i < j < k < l$ we have $c (i l) \neq c (j k)$ .

Next we colour $M_{2}^{(4)}$ as follows: ${i < j < k < l}$ is orange if $c (i k) = c (j l)$ , and white otherwise. Again, by Ramsey’s Theorem for $r$ -sets we can pick an infinite $M_{3} \subset M_{2}$ such that it is monochromatic with respect to this colouring.

We claim that $M_{3}$ cannot be orange. If it is, then we again consider $i < j < k < l < m < n$ :
- ${j < l < m < n}$ gives that $c (j m) = c (l n)$
- ${i < j < k < m}$ gives that $c (j m) = c (i k)$
Hence $c (i k) = c (l n)$ , which contradicts the fact that ${i < j < l < n}$ is blue.

Therefore $M_{3}$ is white. This finally tells us (using earlier working) that given any pair disjoint edges, the colours must be different.

Now, we colour $M_{3}^{(3)}$ via: ${i < j < k}$ yellow if $c (i j) = c (j k)$ , and pink otherwise. By Ramsey’s Theorem for $r$ -sets, there is an infinite $M_{4} \subset M_{3}$ that is monochromatic.

We claim that $M_{4}$ is not yellow. If it is, then given $i < j < k < l$ , we have $c (i j) = c (j k) = c (k l)$ , which contradicts blueness.

Thus for any $i < j < k$ in $M_{4}$ , we have $c (i j) \neq c (j k)$ .

Finally: we colour $M_{4}^{(3)}$ with 4 colours, with ${i < j < k}$ coloured according to:
- turquoise if $c (i j) = c (i k)$ and $c (i k) = c (j k)$
- magenta if $c (i j) = c (i k)$ and $c (i k) \neq c (j k)$
- cyan if $c (i j) \neq c (i k)$ and $c (i k) = c (j k)$
- maroon if $c (i j) \neq c (i k)$ and $c (i k) \neq c (j k)$
By Ramsey’s Theorem for $r$ -sets, there exists a monochromatic set $M_{5} \subset M_{4}$ . It cannot be turquoise because $c (i j) = c (j k)$ contradicts $M_{4}$ . Then:
- magenta implies case (iii)
- cyan implies case (iv)
- maroon implies (ii), i.e. injective. □

Theorem 1.5. Assuming that:

$ℕ^{(r)}$ abitrarily coloured

Then we can find an infinite set

M

and

I \subseteq [r]

such that for any

x_{1} < x_{2} < \dots < x_{r}

M

, and

y_{1} < y_{2} < \dots < y_{r}

M

we have

c (x_{1} x_{2} \dots x_{r}) = c (y_{1} y_{2} \dots y_{r})

if and only if

x_{i} = y_{i}

for all

i \in I

Example. In the previous theorem:

(i) $I = \emptyset$
(ii) $I = {1, 2}$
(iii) $I = {1}$
(iv) $I = {2}$

These $2^{r}$ colourings are call the “canonical colourings” of $ℕ^{(r)}$ .

Proof. Exercise. Note that this proof is examinable (because the ideas are exactly the same as those in the previous theorem). □

1.1 Van der Waerden’s Theorem

We will colour $ℕ$ .

Aim 1: Whenever we $2$ -colour $ℕ$ , we find a monochromatic arithmetic progression of length $m$ for any $m$ .

The abbreviation A.P. can be used to mean “arithmetic progression”, i.e. a sequence of the form ${a, a + d, \dots, a + (m - 1) d}$ .

Aim 2: For any $m$ , there exists $n$ such that whenever $[n]$ are $2$ -coloured, there exists a monochromatic arithmetic progression of length $m$ .

This is equivalent to Aim 1, by using a proof by compactness argument like before:

If Aim 2 is not true, then we can find $c_{n} : [n] \to {1, 2}$ such that infinitely many agree on ${1}$ . Of those infinitely many agree on ${2}$ , etc. Keep going (as before), and then get a colouring of $ℕ$ without a monochromatic arithmetic progression of length $m$ .

The other direction is easier.

We will show something a bit stronger (because it turns out to be easier): we will prove Aim 2 but with $k$ colours.

This is in contrast with the earlier theorems, where the proofs were slightly easier to think about with just 2 colours.

Definition 1.6 (Focused). Let $A_{1}, A_{2}, \dots, A_{k}$ be arithmetic progressions of length $m$ . Say

A_{i} = {a_{i}, a_{i} + d_{i}, \dots, a_{i} + (m - 1) d_{i}} .

We say that these arithmetic progressions are focused if $a_{i} + m d_{i} = f$ for all $i \in [k]$ .

If we have a colouring of $ℕ$ and $A_{1}, \dots, A_{k}$ are focused arithmetic progressions if each $A_{i}$ is monochromatic but they all have different colours, then we call them colour-focused.

Example. ${4, 8}$ and ${10, 11}$ are focused at $12$ .

Theorem 1.7. Assuming that:

$ℕ$ is $k$ -coloured

Then we can find a monochromatic arithmetic progression of length

3

(equivalently, for any

k

we find an

n

that works).

Proof. Claim: For any $r \leq k$ there exists an $n$ such that if $[n]$ is $k$ -coloured then either:

there exists a monochromatic arithmetic progression of length $3$
there exists $r$ colour-focused arithmetic progressions of length $2$

The proof is by induction on $r$ .

Base case $r = 1$ we can take $n = k + 1$ , since 2 numbers will have the same colour.

Suppose the result is true for $r - 1$ and let $n$ be an $n$ that satisfies the property in the claim.

We will show that $N = (k^{2 n} + 1) 2 n$ works for $r$ . Let $c : [(k^{2 n} + 1) 2 n] \to [k]$ be a colouring. We will split the ground set into $k^{2 n} + 1$ blocks of length $2 n$ . Call the blocks $B_{i}$ .

If there exists a monochromatic arithmetic progression of length $3$ in this colouring, then we are done. So assume not.

By the induction hypothesis, the first half of each $B_{i}$ has $r - 1$ colour-focused arithmetic progressions of length $2$ . Because $| B_{i} | = 2 n$ , each block also contains their focus.

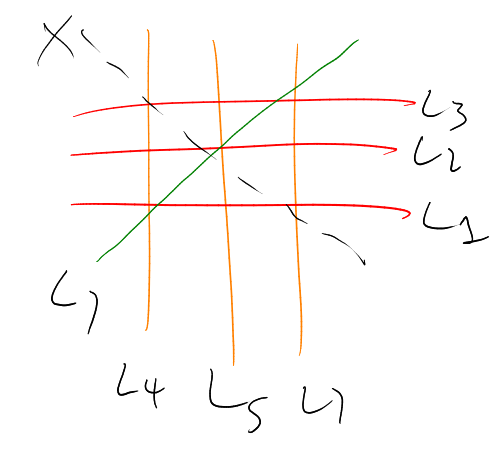
For a set $| M | = 2 n$ , there are exactly $k^{2 n}$ ways to $k$ -colour it. So there exists two blocks $B_{p}$ and $B_{p + t}$ that are identically coloured.

Let ${a_{i}, a_{i} + d_{i}}$ be the $r - 1$ colour-focused arithmetic progressions in $B_{p}$ . Then ${a_{i} + 2 n t, a_{i} + d_{i} + 2 n t}$ are the corresponding ones in $B_{p + t}$ . Let $f$ be the focus in $B_{p}$ , so therefore $f + n t$ is the focus in $B_{p + t}$ .

Now take ${a_{i}, a_{i} + d_{i} + 2 n t}$ for $i \in [r - 1]$ , and ${f, f + 2 n t}$ . Since $a_{i} + 2 d_{i} = f$ , we have $a_{i} + 2 d_{i} + 4 n t = f + 4 n t$ . So all $r$ of these sequences are focused at $f + 4 n t$ .

We know that ${a_{i}, a_{i} + d_{i} + n t}$ and ${f, f + 2 n t}$ are monochromatic by the choice of $B_{p}$ , $B_{p + t}$ . Why colour focused? ${a_{i}, a_{i} + 2 n t}$ have different colours by induction hypothesis. Also, because $c$ was assumed to have no monochromatic arithmetic progression of length $3$ , the colours of ${f, f + 2 n t}$ must be different to all the colours of the above $r - 1$ arithmetic progressions of length $2$ . Thus we have $r$ colour-focused arithmetic progressions of length $2$ in $[(k^{2 n} + 1) 2 n]$ . □

Remark. The idea of looking at all the possible colouring of a set is referred to as the “product argument”.

The Van der Waerden number $W (k, m)$ is the smallest $n$ such that whenever $[n]$ is $k$ -coloured, there exists a monochromatic arithmetic progression of length $m$ .

Proof above claims that $W (k, 3) \leq k^{k^{. . . msup k^{4 k}}}$ for a tower of size $k - 1$ . “tower-type bound”.

Theorem 1.8 (Van der Waerden). Assuming that:

$k, m \in ℕ$

Then there exists an

n \in ℕ

such that whenever we

k

-colour

[n]

we can find a monochromatic arithmetic progression of length

m

Recall that we defined $W (k, m)$ to be the smallest $n$ (if it exists) such that whenever $[n]$ is $k$ -coloured, there exists a monochromatic arithmetic progression of length $m$ .

Proof. This will be by induction on $m$ . For any $k$ :

$m = 1$ is trivial.

$m = 2$ is pigeonhole.

$m = 3$ is Theorem 1.7.

Assume that this is true for some $m - 1$ fixed, but for any $k$ . In other words, $W (k, m - 1)$ exists for all $k \geq 1$ .

Claim: For every $r \leq k$ there exists $n$ such that we always have one of the following:

have a monochromatic arithmetic progression of length $m$
$r$ colour-focused arithmetic progressions of length $m - 1$

When $r = k$ we are done by looking at the focus. Now we prove the claim. We will prove it by induction on $r$ .

For $r = 1$ we can take $n = W (k, m - 1)$ .

Now assume that the result is true for $r - 1$ and that there does not exist a monochromatic arithmetic progression of length $m$ . We will show that $n$ works for $r - 1$ , then $W (k^{2 n}, m - 1) 2 n$ will work for $r$ .

Aim: whenever we $k$ -colour $[W (k^{2 n}, m - 1) 2 n]$ we can find $r$ colour-focused arithmetic progressions of length $m - 1$ . Let $B_{1} = {1, 2, \dots, 2 n}$ , $B_{2} = {2 n + 1, \dots, 4 n}$ etc, i.e. $B_{i} = [2 n (i - 1) + 1, 2 n i]$ for $i \in {1, \dots, W (k^{2 n}, m - 1)}$ .

Let us look at the indices of these blocks. I colour $i$ with $k^{2 n}$ colours like so:

c^{'} (i) = (c (2 n (i - 1) + 1), c (2 n (i - 1) + 2), \dots, c (2 n i)) .

We therefore colour $[W (k^{2 n}, m - 1)]$ with $k^{2 n}$ colours. By the definition of $W$ , there exists a monochromatic arithmetic progression of length $m - 1$ (with respect to $c^{'}$ ). Say $α, α + t, \dots, α + (m - 2) t$ .

So the respective blocks $B_{α}, B_{α + 2 t}, \dots, B_{α + (m - 2) t}$ are identically coloured. Look at $B_{α}$ . It has length $2 n$ , so by induction $B α$ contains $r - 1$ colour-focused arithmetic progressions of length $m - 1$ together with their focus.

Let $A_{i} = {a_{i}, a_{i} + d i, \dots, a_{i} + (m - 2) d i}$ for $i \in {1, \dots, r - 1}$ . Let $f$ be their focus. Look at $B_{i} = {a_{i}, a_{i} + d i + 2 n t, a_{i} + 2 d i + 4 n t, \dots, a_{i} + (m - 2) d i + 2 (m - 2) t}$ , $i = 1, \dots, r - 1$ .

They are monochromatic because the blocks are identically coloured and the $B_{i}$ s are monochromatic. Since the colour of $A_{i}$ is the colour of $B_{i}$ and the $A_{i}$ s are colour-focused, we must have that the $B_{i}$ s have pairwise distinct colours.

Remember that the $A_{i}$ s are are focused at $f_{i}$ and the colour of $f_{i}$ is different than the colour of all the $A_{i}$ s. Note $f_{i} = a_{i} + (m - 1) d i$ .

Look at $A = {f, f + 2 n t, 2 + 4 n t, \dots, f + 2 n (m - 2) t}$ . This is an arithmetic progression of length $m - 1$ and monochromatic and of a different colour from all of the $A_{i}$ s.

Enough to show $a_{i} + (m - 1) (d i + 2 n t) = f + 2 n (m - 1) t$ for all $i$ , which is equivalent to $a_{i} + (m - 1) d i = f$ , which is true as all the $B_{i}$ s are focused at $f$ . □

Non-examinable: what about bounds?

We define the Ackermann hierarchy to be the seqeunce of functions

f_{1}, f_{2}, \dots, f_{n} : ℕ \to ℕ

\begin{array}{l} f_{1} (x) & = 2 x \\ f_{n + 1} (x) & = f_{n}^{(x)} (1) = \underset{x times}{\underset{⏟}{f_{n} (f_{n} (\dots f_{n} (1)))}} \end{array}

Observe:

\begin{array}{l} f_{2} (x) & = x \\ f_{3} (x) & = 2^{2^{2^{. . . msup 2}}} & x times \\ f_{4} (1) & = 2 \\ f_{4} (2) & = 2^{2} = 4 \\ f_{4} (3) & = 2^{2^{2^{2}}} = 65536 \\ f_{4} (4) & = 2^{2^{. . . msup 2}} & 65536 times \end{array}

These functions grow very fast.

We say that a function $f : ℕ \to ℕ$ is of type $n$ if there exists $c, d$ such that

f (c x) \leq f_{n} (x) \leq f (d x) .

Our bound on $W (k, 3)$ was of type $3$ .

If you check our proof carefully, then $W (k, m)$ (as a function of $k$ ) is bounded by a “type $m$ ” bound.

Define: $W (m) = W (2, m)$ . Then our proof gives a bound that grows faster than any $f_{n}$ .

Remark. This is often a feature of a double induction proof.

It was believed that $W (m)$ does indeed grow this fast.

Shelah (1987) found a proof by just induction on $m$ , and showed that $W (k, m) \leq f_{4} (m + k)$ .

A prize of $1000 was placed by Graham to show that $W (m) \leq f_{3} (m)$ .

Gowers (1998) showed that $W (m) \leq 2^{2^{2^{2^{2^{m + 9}}}}}$ , which is “almost type 2”.

The best lower bound is $W (m) \geq \frac{2^{m}}{8 m}$ .

Corollary. Whenever $ℕ$ is finitely coloured, there exists a colour class that contains arbitrarily long arithmetic progressions.

What about infinite monochromatic arithmetic progressions

No, for example:

(1) colour ${1, 2}$ red, ${3, 4, 5}$ blue, ${6, 7, 8, 9}$ red, etc
(2) Or “just do it”: the set of arithmetic progressions in $ℕ$ is countable. So let them be $A_{1}, A_{2}, \dots, A_{k}, \dots$ . Pick $x_{1} < y_{1}$ in $A_{1}$ , and colour $x_{1}$ red, $y_{1}$ blue. Next go to $A_{2}$ and select $x_{1} < y_{1} < x_{2} < y_{2}$ in $A_{2}$ . Colour $x_{2}$ red, $y_{2}$ blue. Keep going...

Theorem 1.9 (Strengthened Van Waerden). Assuming that:

$m, k \in ℕ$

Then there exists

n

such that whenever

[n]

k

-coloured, there exists a monochromatic arithmetic progression of length

m

together with their common differences, i.e. the set

{d, a, a + d, \dots, a + (m - 1) d}

is monochromatic.

Proof. By induction on the number of colours. $k = 1$ is trivial.

Assume that the case for $k - 1$ colours is true. So there exists $n$ that works for $m$ and $k - 1$ .

We will show that $W (k, n (m - 1) + 1)$ works for $m$ and $k$ . If $[W (k, n (m - 1) + 1)$ are $k$ -coloured, then there exists a monochromatic arithmetic progression (say red) of length $n (m - 1) + 1$ , say $a, a + d, \dots, a + d n (m - 1)$ .

If any of $d, 2 d, \dots, n d$ is red, then we are done: e.g. $a, a + r d, \dots, a + r (m - 1) d$ for some $r \in [n]$ .

If not, the set ${d, 2 d, \dots, n d}$ is $k - 1$ -coloured.. This involves a $(k - 1)$ colouring on $[n]$ , therefore there exist $b, b + r, \dots, b + (m - 1) r$ and $r$ the same colour. This translates to $d b, d b + r, \dots, d b + d (m - 1) r, d r$ monochromatic. □

Remark. $m = 2$ is known as Schur’s Theorem: we can always find $a, a + d, d$ monochromatic (for finite colouring of $ℕ$ ). In other words, there exists a monochromatic solution to $x + y = z$ .

Can deduce Schur from Ramsey for pairs: $c : ℕ \to [k]$ then we induce $c^{'} : ℕ^{(2)} \to [k]$ as follows: $c^{'} (i j) = c (j - i)$ . By Ramsey’s Theorem for $r$ -sets, there exists $i < j < k$ such that $c^{'} (i j) = c^{'} (i k) = c^{'} (j k)$ . Then

c (\underset{x}{\underset{⏟}{j - i}}) = c (\underset{z}{\underset{⏟}{k - i}}) = c (\underset{y}{\underset{⏟}{k - j}}) .

Get $x + y = z$ and $x, y, z$ monochromatic.

1.2 The Hales-Jewett Theorem

Let $X$ be a finite set and $X^{n}$ is words of length $n$ on the alphabet $X$ .

Definition 1.10 (Combinatorial line). A combinatorial line in $X^{n}$ is a set of the following form:

{(x_{1}, \dots, x_{n}) \in X^{n} : \exists I \subseteq [n], a_{i} \in X, I \neq \emptyset, x_{i} = a_{i} \forall i \notin I, x_{i} = x_{j} \forall i, j \in I} .

Example. $X = [3]$ and we want combinatorial lines in ${[3]}^{2}$ . If $I = {1}$ , we get:

\begin{array}{l} L_{1} & = {(1, 1), (2, 1), (3, 1)} \\ L_{2} & = {(1, 2), (2, 2), (3, 2)} \\ L_{2} & = {(1, 3), (2, 3), (3, 3)} \end{array}

If $I = {2}$ we get:

\begin{array}{l} L_{4} & = {(1, 1), (1, 2), (1, 3)} \\ L_{5} & = {(2, 1), (2, 2), (2, 3)} \\ L_{6} & = {(3, 1), (3, 2), (3, 3)} \end{array}

$I = {1, 2}$ , then

L_{7} = {(1, 1), (2, 2), (3, 3)} .

Example. ${[3]}^{3}$ , $I = {1}$ $(1, 2, 3), (2, 2, 3), (3, 2, 3)$ , or if $I = {1, 3}$ $(1, 3, 1), (2, 3, 2), (3, 3, 3)$ .

Note. The definition of a combinatorial line is invariant under permutations of $X$ .

Theorem 1.11 (The Hales-Jewett Theorem). Assuming that:

$m, k \in ℕ$

Then there exists

n

such that whenever we

k

-colour

{[m]}^{n}

there exists a monochromatic combinatorial line.

Remark.

(1) The smallest such $n$ is call $H J (m, k)$ .

(2) The Hales-Jewett Theorem implies Van der Waerden:

Proof. Let $c$ be a finite colouring of $ℕ$ . Let $n$ be large enough ( $= H J (m, k)$ )and now colour ${[m]}^{n}$ . $m$ is the length of desired arithmetic progression. Define

c^{'} ((x_{1}, x_{j}, \dots, x_{n})) = c (x_{1} + x_{2} + \dots x_{n}) .

By The Hales-Jewett Theorem, there exists a monochromatic line

□

Exercise: Suppose you play Naughts and Crosses with $m$ in a line and you play it in high enough dimensions. Show it cannot be a draw (assuming optimal play). Moreover, it is a first player win. Hint: Strategy stealing.

Definition 1.12. If I have a combinatorial line $L$ in ${[m]}^{n}$ , then I can order $x \leq y$ if and only if $x_{i} \leq y_{i}$ for all $i$ . Let $L^{-}$ denote the first point in this ordering, and let $L^{+}$ denote the last point in this ordering.

Definition 1.13. Let $L_{1}, \dots, L_{k}$ be combinatorial lines. We call them focussed if $L_{i}^{+} = f$ for all $i \in [k]$ . For a fixed colouring, they are colour focused if they are focused and $L_{i} ∖ {L_{i}^{+}}$ monochromatic for each $i$ , and they have different colours.

Example. ${[4]}^{2}$

are $3$ colour-focused combinatorial lines ${[4]}^{2}$ .

Proof of The Hales-Jewett Theorem. The proof is by induction on the size of the alphabet, i.e. $m$ .

$m = 1$ is trivially true.

Assume $m \geq 1$ and assume $H J (m - 1, k)$ exists for all $k$ .

Claim: for every $1 \leq r \leq k$ there exists $n$ such that in ${[m]}^{n}$

(1) either there exists monochromatic combinatorial lines
(2) there exists $r$ colour-focused combinatorial lines

Then we are done by $r = k$ and looking at the focus.

Now we prove the claim:

$r = 1$ : look in ${[m - 1]}^{n^{'}} \subset {[m]}^{n}$ We can take $H J (m - 1, k)$ .

Now assume $r > 1$ and that $n$ is suitable for $r - 1$ . We will show that $n + H J (m - 1, k^{m^{n}})$ is suitable for $r$ . Let $N = H J (m - 1, k^{m^{n}})$ for convenience.

Need: given $c$ a $k$ -colouring of ${[m]}^{n + N}$ with no monochromatic combinatorial lines, we can find $r$ colour-focused combinatorial lines. Look at ${[m]}^{n + N}$ as ${[m]}^{n} \times {[m]}^{N}$ , with ${[m]}^{n} = {a_{1}, \dots, a_{m^{n}}}$ .

Let us colour ${[m]}^{N}$ as follows:

c^{'} : {[m]}^{N} \to k^{m^{n}} c^{'} (b) = (c (a_{1}, b), c (a_{2}, b), \dots, c (a_{m^{n}}, b)) .

By The Hales-Jewett Theorem there exists a combinatorial lines $L$ with active coordinates $I$ such that

c (a, b) = c (a, b^{'}) \forall a \in {[m]}^{n}, \forall b, b^{'} \in L ∖ {L^{+}} .

But now this induces $c^{″} : {[m]}^{n} \to k$ where $c^{″} (a) = c (a, b)$ for any $b \in L ∖ {L^{+}}$ . By the definition of $n$ , there exist $r - 1$ colour-focused combinatorial lines (for $c^{″}$ ) $L_{1}, L_{2}, \dots, L_{r - 1}$ , focused at $f$ , and with active coordinates $I_{1}, I_{2}, \dots, I_{r - 1}$ .

Finally: look at the combinatorial lines that start at $L_{i}^{-} \times L^{-}$ and active coordinates $I_{i} \cup I$ . These give $r - 1$ combinatorial lines, and the combinatorial lines that starts at $f \times L^{-}$ with active coordinates $I$ . All focused at $f \times L^{+}$ . Then done. □

Definition 1.14 ( $d$ -dimensional space). A $d$ -dimensional space $S \subseteq X^{n}$ or a $d$ -point parameter set is a set such that there exists $I_{1}, I_{2}, \dots, I_{d} \subseteq [n]$ disjoint and $a_{i} \in X \forall i \in [n] ∖ (I_{1} \cup \dots \cup I_{d})$ , and $x \in S$ if and only if:

$x_{i} = a_{i}$ for all $i \in [n] ∖ (I_{1} \cup \dots \cup I_{d})$
$x_{i} = x_{i}$ if $i, j \in I_{d}$ for some $l \in [d]$

Theorem 1.15 (The Extended Hales-Jewett Theorem). Assuming that:

$m, k, d$ positive integers

Then there exists

n

such that whenever

{[m]}^{n}

k

-coloured, there exists a

d

-point parameter set monochromatic.

Proof. In $X^{n^{'} d} = {(X^{d})}^{n^{'}} = Y^{n^{'}}$ what does a combinatorial line in $Y^{n^{'}}$ look like?

So a monochromatic line in $Y^{n^{'}}$ is a monochromatic $d$ -point parameter set in $X^{n^{'} d}$ .

Letting $n = d H J (m^{d}, k)$ works. □

Definition 1.16 (Homothetic copy). Let $S$ be a finite set of points in $X^{n}$ . A homothetic copy of $S$ is a set of the form $x + λ S$ .

Theorem 1.17 (Gallai’s Theorem). Assuming that:

finite $S \subset ℕ^{d}$
$k$ -colouring of $ℕ^{d}$

Then there exists a monochromatic homothetic copy of

S

Proof. $S = {S_{1}, \dots, S_{m}}$ . Let $c : ℕ^{d} \to k$ be a colouring.

We colour ${[m]}^{n}$ (for $n$ large enough) as follows:

c^{'} ((x_{1}, \dots, x_{n})) = c (S_{x_{1}} + S_{x_{2}} + \dots + S_{x_{m}}) .

By The Hales-Jewett Theorem, there exists a monochromatic combinatorial line in ${[m]}^{n}$ with active coordinates $I$ . Then

c (\sum_{inactive} S_{i} + | I | S_{j})

has the same colour for all $j \in [m]$ .

Done as this is a copy of $S$ translate by $\sum_{inactive} S_{i}$ , and dilation factor $| I |$ . □

Remark.

(1) You can prove Gallai with a standard focusing + product argument.
(2) The Hales-Jewett Theorem for $2$ -point parameter set on $X = {1, 2}$ gives a rectangle, while Gallai’s Theorem can give a square.

2 Partition Regular Equations

Schur’s theorem: $x + y = z$ has monochromatic solutions (if $ℕ$ is finitely coloured).

Van der Waerden: $x_{1}, x_{2}, y_{1}, \dots, y_{m}$ such that the system

\begin{array}{l} y_{1} & = x_{1} + x_{2} \\ y_{2} & = x_{1} + 2 x_{2} \\ ⋮ \\ y_{m} & = x_{1} + m x_{2} \end{array}

has a monochromatic solution.

Main aim: decide when a system of equations is ‘partition regular’.

Definition (Partition regular). Let $A \neq 0$ be a $m \times n$ matrix over $ℚ$ and we say that $A$ is partition regular (PR) if whenever $ℕ$ is finitely coloured, there exists a monochromatic $x \neq 0$ such that $A x = 0$ .

Example.

(1) Schur: says $(1, 1, - 1)$ is partition regular.
(2) Van der Waerden: says
$(\begin{matrix} 1 & 1 & - 1 & 0 & \dots & 0 \\ 1 & 2 & 0 & - 1 & \dots & 0 \\ 1 & 3 & 0 & 0 & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & m & 0 & 0 & \dots & - 1 \end{matrix})$

is partition regular.
(3) $(1, - 1)$ is partition regular.
(4) $(3, 4, - 7)$ is partition regular (just take all to be equal).
(5) $(3, 4, - 6)$ ? Don’t know yet.
(6) Non-example: $(2, - 1)$ . Need $2 x = y$ . Colour $ℕ$ by setting $n$ to be red if the biggest power of $2$ dividing it is even, and blue otherwise.

Definition (Column property). We say that a rational matrix

A = (\begin{matrix} ↑ & ↑ & \dots & ↑ \\ c_{1} & c_{2} & \dots & c_{n} \\ ↓ & ↓ & \dots & ↓ \end{matrix})

has the column property (CP) if there exists a partition of $[n] = B_{1} ⊔ B_{2} \dots ⊔ B_{r}$ such that:

(1) $\sum_{i \in B_{1}} c_{i} = 0$
(2) $\sum_{i \in B_{t}} c_{i} \in span ⟨ c_{j} : j \in B_{1} \cup B_{2} \cup \dots B_{t - 1} ⟩$ (note that it doesn’t make a difference whether the span is the $ℝ$ -linear or $ℚ$ -linear span)

Example.

(1) $(1, 1, - 1)$ can take $B_{1} = {1, 3}$ , $B_{2} = {2}$ , hence it does have the column property.
(2) Van der Waerden matrix from (2) in the previous example: take $B_{1} = {1, 3, 4, \dots, n}$ and $B_{2} = {2}$ , which shows that it has the column property.
(3) $(3, 4, - 7)$ , take $B_{1} = {1, 2, 3}$ so it has column property.
(4) $(2, - 1)$ does not have column property.
(5) $(λ, - 1)$ has column property if and only if $λ = 1$ .
(6) $(3, 4, - 6$ doesn’t have the column property.

Aim:

Theorem 2.1 (Rado’s Theorem). A matrix over $ℚ$ is partition regular if and only if it has the column property.

Remark.

(1) partition regular is checkable in finite time.
(2) Find $a, b \in ℕ$ such that
$(\begin{matrix} 1 & - 1 & 3 \\ 2 & - 2 & a \\ 4 & - 4 & b \end{matrix})$

is partition regular. Take $(a, b) = (6, 12)$ .
(3) Neither direction of Rado’s Theorem is easy (or obvious)!

Today we will look at a single equation, i.e. a single row matrix.

If we have $x = (a_{1}, \dots, a_{n})$ a $1 \times n$ matrix, then $x$ is partition regular if and only if $λ x$ is also partition regular. So we may assume that $a_{i} \in ℤ$ .

Observation: $(a_{1}, \dots, a_{n})$ has the column property if and only if there exists a set ${a_{i_{1}}, \dots, a_{i_{k}}}$ of non-zero elements such that $\sum_{k = 1}^{n} a_{i_{k}} = 0$ ( $*$ ).

Also note that we may assume that $a_{i} \neq 0$ .

We are going to show that if $x$ partition regular then it has the column property, which is equivalent to ( $*$ ) in this case.

Remark. Even in this case, neither direction of Rado’s Theorem is easy.

Definition. Let $x \in ℕ$ and $p$ a prime. Then we can write

x = a_{k} p^{k} + \dots + a_{1} p + a_{0},

with $0 \leq a_{i} < p$ . Denote by $e (x) = {a_{t} : t = \min, c b i : a_{i} \neq 0}$ .

Example.

Proposition 2.2. If $A = (a_{1}, \dots, a_{n})$ , $a_{i} \neq 0$ is partition regular then it has the column property.

Proof. Let $p$ be a huge prime, $p > \sum | a_{i} |$ . I give to the number $x$ the colour $e (x) \in {0, \dots, p - 1}$ . Then by assumption, there exists $x_{1}, \dots, x_{n}$ of the same colour such that $\sum a_{i} x_{i} = 0$ .

In symbols, let $t = \min {t (x_{1}), \dots, t (x_{n})}$ , $I = {i : t (x_{i}) = t}$ . When we sum $\sum_{i \in [n]} a_{i} x_{i} = 0$ and we look at the last digit $mod p$ , we get $\sum_{i \in I} a_{i} d = 0$ , where $d$ is the colour of our $x_{i}$ s. Then $d (\sum_{i \in I} a_{i}) \equiv 0 (m o d p)$ . Then $\sum_{i \in I} a_{i} = 0$ (and note $I$ is non-empty). □

Remark. To this day, there are no other known proofs of this proposition.

Currently looking at: single equation, i.e. vectors $(a_{1}, \dots, a_{n})$ , $a_{i} \in ℚ ∖ {0}$ .

Showed that if $(a_{1}, \dots, a_{n})$ is partition regular then it has the column property (recall that in this one dimensional case, having the column property is the same as there exists $I \neq \emptyset$ such that $\sum_{i \in I} a_{i} = 0$ ).

The other direction:

We want to take a vector $(a_{1}, \dots, a_{n})$ with $\sum_{i \in I} a_{i} = 0$ and show that it is partition regular.

For $(a, 1)$ we know that it is partition regular if and only if $a = 1$ .

For length $3$ , $(1, λ, - 1)$ is the only non-trivial case with column property. Note $λ = 1$ is Schur’s theorem.

Lemma 2.3. Assuming that:

$λ \in ℚ$

Then for any finite colouring of

ℕ

, there exists a monochromatic solution to

x + λ y = z

Remark. We in fact show that whenever $[n]$ is $k$ -coloured ( $n = n (k)$ ), then we have a monochromatic solution.

Proof. If $λ = 0$ then nothing to show.

If $λ < 0$ then $z - λ y = x$ , so these are equivalent.

Assume $λ > 0$ , $λ = \frac{r}{s}$ , $r, s \in ℕ$ .

Seek solution to $x + \frac{r}{s} = z$ . Let $c : ℕ \to [k]$ be a finite colouring. Prove this by induction on $k$ .

$k = 1$ trivial.

Assume this is true for $k - 1$ and we want to show it for $k$ . Assume $n$ is suitable for $k - 1$ . We show that $W (k, n r + 1) n s$ is suitable for $k$ .

We now have $[W (k, n r + 1)]$ $k$ -coloured. There exists a monochromatic arithmetic progression of length $n r + 1$ , say $a, a + d, \dots, a + d n r$ of colour red. Let us look at $d i s$ , where $i \in [n]$ . Note $d i s \leq W (k, n r + 1) n s$ , so “it is in our set of coloured numbers”.

If $d i s$ is also red, then $a, a + i r d, d i s$ is a monochromatic solution.

If no such $d i s$ exists, then ${d s, 2 d s, \dots, n d s}$ is $k - 1$ coloured. So there exists $i, j, k$ such that $c (i d s) = c (j d s) = c (k d s)$ and $i + λ j = k$ . Then $d s i + λ d s j = d s k$ , i.e. $d s i, d s j, d s k$ is a monochromatic solution. □

Remark.

(1) This is “manually” same proof for Strengthened Van Waerden.
(2) $λ = 1$ is Schur’s theorem (which you can prove by Ramsey). The general case ( $λ \in ℚ$ ) does not seem to be a proof “by Ramsey”.

Theorem 2.4 (Rado’s Theorem for single equation). Assuming that:

$(a_{1}, \dots, a_{n}) \in ℚ^{n}$

Then it is partition regular if and only if it has the column property.

Proof. We saw in Proposition 2.2 that if it is partition regular then it has the column property.

For the other direction, we know that $\sum_{i \in I} a_{i} = 0$ and we need to show that given $c : ℕ \to [k]$ such that there exists monochromatic $(x_{1}, \dots, x_{n})$ such that $\sum a_{i} x_{i} = 0$ .

Fix $i_{0} \in I$ and we “cook up” the following vector:

x_{i} = {\begin{matrix} x & if i = i_{0} \\ y & if i \notin I \\ z & if i \in I ∖ {i_{0}} \end{matrix}

Need $x, y, z$ monochromatic such that $(\sum_{i \notin I} a_{i}) y + x a_{i_{0}} + (\sum_{i \in I ∖ {i_{0}}} a_{i}) z = 0$ , which is the same as requiring $x a_{i_{0}} - z a_{i_{0}} + (\sum i \notin I a_{i}) y = 0$ .

Upon dividing by $a_{i_{0}}$ , we see that this is the same as

x + (\frac{\sum_{i \notin I} a_{i}}{a_{i_{0}}}) y = z,

which is true by Lemma 2.3. □

Remark. Rado’s Boundedness Conjecture: Let $A$ be an $n \times m$ matrix that is not partition regular. In other words, there exists a bad $k$ -colouring for some $k$ . Is this $k$ bounded, i.e. $k = k (m, n)$ ?

This is known for $1 \times 3$ matrices (Fox, Kleitman, 2006). $24$ colours suffices in this case.

Onto the general case for Rado’s Theorem.

Recall that for a prime $p$ and $x \in ℕ$ , $e (x) = last non-zero digit in base p$ .

Also recall $t (x) = position on which you find e (x)$ .

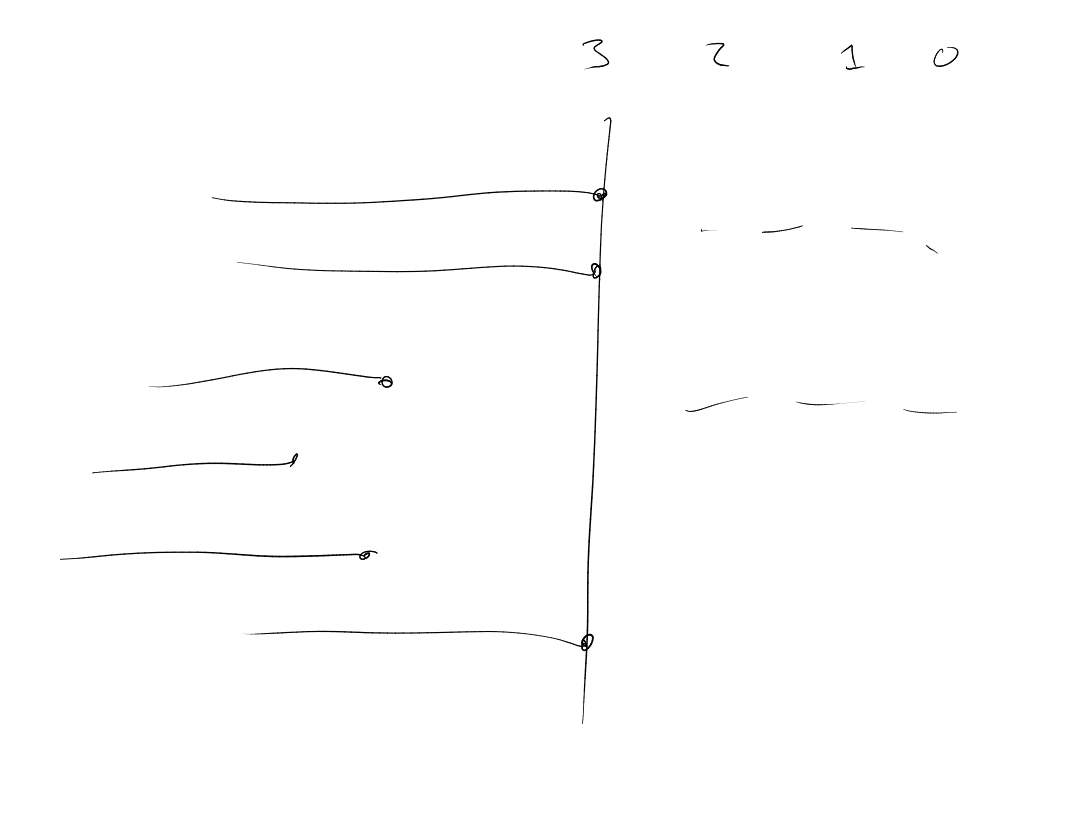
Proposition 2.5. Assuming that:

$A$ a matrix with entries in $ℚ$
$A$ is partition regular

Then

A

has the column property.

Proof. Let $C_{1}, \dots, C_{n}$ be its columns. Fix $p$ prime.

Colour $ℕ$ as we did before, by $c (x) = e (x)$ . By assumption there exists monochromatic $x_{1}$ such that $\sum_{i} x_{i} C_{i} = 0$ .

Let us partition $C_{1}, \dots, C_{n}$ as $B_{1} ⊔ B_{2} ⊔ \dots ⊔ B_{l}$ where $i, j \in B_{k}$ if and only if $t (x_{i}) = t (x_{j})$ , $i \in B_{k_{1}}$ , $j \in B_{k_{2}}$ for $k_{1} < k_{2}$ if and only if $t (x_{i}) < t (x_{j})$ .

We do this for infinitely many $p$ . Because there exist finitely many partitions, for infinitely many primes $p$ we will have the same blocks.

For $B_{1}$ : $\sum_{i} x_{i} C_{i} = 0$ , say all have colour $d$ , i.e. $e (x_{i}) = d \in [1, \dots, p - 1]$ . Then $\sum d C_{i} \equiv 0 (mod p)$ (by collecting the right-most terms in base $p$ ). Since this holds for infinitely many $p$ , we have that $\sum_{i \in B_{i}} C_{i} = 0 (mod p)$ for infinitely many primes (the large primes), and hence we have that $\sum_{i \in B_{i}} C_{i} = 0$ .
$\sum_{i \in B_{k^{'}}} p^{t} d C_{i} + \sum_{i \in B_{1}, \dots B_{k^{'} - 1}} x_{i} C_{i} \equiv 0 (mod p^{t + 1})$ .

Then $\sum_{i \in B_{k}} p^{t} C_{i} + \sum_{i \in B_{1}, \dots, B_{k^{'} - 1}} x_{i} {(d)}^{- 1} C_{i} \equiv 0 (mod p^{t + 1})$ ( $*$ ).

Claim: $\sum_{i \in B_{k}} C_{i} \in {span}_{i \in B_{1} \cup \dots \cup B_{k - 1}} ⟨ C_{i} ⟩$ .

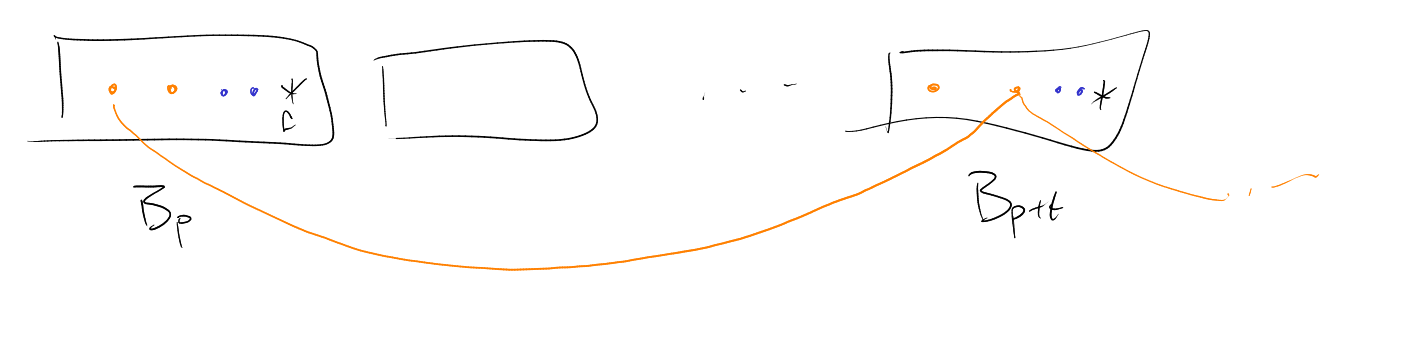
We will show that given $U$ such that $U \cdot C_{i} = 0$ got sll $i \in B_{1}, \dots, B_{k - 1}$ . Then
$u \cdot (\sum_{i \in B_{k}} C_{i}) = 0$

which finishes the proof as this implies $\sum_{i \in B_{k}} C_{i} \in {span}_{i \in B_{1} \cup \dots \cup B_{k - 1}} ⟨ C_{i} ⟩$ . Take the inner product of ( $*$ ) with $u$ . Get
$p^{t} \sum_{i \in B_{k}} u \cdot C_{i} \equiv 0 (mod p^{t + 1}),$

which is equivalent to $\sum_{i \in B_{k}} u \cdot C_{i} \equiv 0 (mod p)$ . Since this happens for infinitely many $p$ , we get $\sum_{i \in B_{k}} u \cdot C_{i} = 0$ . □

A crucial notion that puts things into perspective is:

Definition ( $(m, p, c)$ -set). An $(m, p, c)$ -set $S \subseteq ℕ$ ( $m$ the number of generators, $p$ the range of coefficients, $c$ the leading coefficient) with $x_{1}, x_{2}, \dots, x_{m}$ is the set of the following form:

S = {\sum_{i = 1}^{m} λ_{i} x_{i} : \exists j, λ_{j} = c and \forall i < j, λ_{i} = 0, and \forall k > j, λ_{k} \in [- p, p]}

\begin{array}{l} c x_{1} + λ_{2} x_{2} + λ_{3} x_{3} + \dots + λ_{m} x_{m} & λ_{i} \in [- p, p] \\ c x_{2} + λ_{3} x_{3} + \dots + λ_{m} x_{m} & λ_{i} \in [- p, p] \\ ⋮ \\ c_{m} x_{m} & λ_{i} \in [- p, p] \end{array}

We call these the rows of the

(m, p, c)

-set.

Remark. An $(m, p, c)$ -set is sort of a progression of progressions.

Example.

1. $(2, p, 1)$ -set: generators $x_{1}, x_{2}$ . Have $x_{1} - p x_{2}, x_{1} - (p - 1) x_{2}, \dots, x_{1} + p x_{2}$ , then $x_{2}$ . This is an arithmetic progression of length $2 p + 1$ with its common difference.
2. $(2, p, 3)$ -set: $3 x_{1} - p x_{2}, 3 x_{1} - (p - 1) x_{2}, \dots, 3 x_{1} + p x_{2}$ , then $3 x_{2}$ . This is an arithmetic progression of length $2 p + 1$ with $3$ times its common difference, and its middle term is divisible by $3$ .

Theorem 2.6. Assuming that:

$m, p, c$ in $ℕ$
a finite colouring of $ℕ$

Then there exists a monochromatic

(m, p, c)

-set.

Remark. An $(M, p, c)$ -set with $M \geq m$ contains a $(m, p, c)$ -set.

Proof. By the above remark, it is enough to find a $(k (m - 1) + 1, p, c)$ -set set such that each row is monochromatic.

Let $n$ be large enough (enough in order to apply everything to follow). Let $A_{1} = {c, 2 c, \dots, c ⌊ \frac{n}{c} ⌋}$ . By Van der Waerden, there exists a monochromatic arithmetic progression of length $2 n_{1} + 1$ , with $n_{1}$ is large enough.

R_{1} = {c x_{1} - n_{1} d_{1}, c x_{1} - (n_{1} - 1) d_{1}, \dots, c x_{1} n_{1} d_{1}}

has colour $k_{1}$ . Let $M = m (k - 1) + 1$ . Now we restrict attention to

B_{1} = {d_{1}, 2 d_{1}, \dots, ⌊ \frac{n}{(M - 1) p} ⌋ d_{1}} .

Observe that $c x_{1} + λ_{1} b_{1} + λ_{2} b_{2} + \dots + λ_{M - 1} b_{M - 1}$ where $b_{i} \in B_{i}$ , $λ_{i} \in [- p, p]$ is in $R_{1}$ for any $λ_{i} \in [- p, p]$ and any $b_{1}, \dots, b_{M - 1}$ . Thus has colour $k_{1}$ .

Next: look inside $B_{1}$ :

A_{2} = {c d_{1}, 2 c d_{1}, \dots, ⌊ \frac{n_{1}}{(M - 1) p c} ⌋ c d_{1}} .

Apply Van der Waerden to find an arithmetic progression of length $2 n_{2} + 1$ , of colour $k_{2}$ . Let

R_{2} = {c x_{2} - n_{2} d_{2}, c x_{2} - (n_{2} - 1) d_{2}, \dots, c x_{2} + n_{2} d_{2}},

of colour $k_{2}$ , and let

B_{2} = {d_{2}, 2 d_{2}, \dots, ⌊ \frac{n_{2}}{(M - 2) p_{2}} ⌋ d_{2}} .

Note that for any $b_{1}, \dots, b_{M - 2}$ and $λ_{1}, \dots, λ_{M - 2} \in [- p, p]$ . Then

c x_{2} + λ_{1} b_{1} + \dots + λ_{M - 2} b_{M - 2}

is in $R_{2}$ , thus has colour $k_{2}$ .

Keep on doing this $M$ times. Restrict to $M$ generators (by setting some $λ$ to $0$ ). □

Remark. For the sake of exams (and also in general):

Being “super” pedantic about $⌊ ∙ ⌋$ and bounds is not that important.

The idea is important.

Theorem 2.7 (Finite Sums Theorem). Let $m$ be fixed. Then whenever we finitely colour $ℕ$ , there exist ${x_{1}, \dots, x_{m}}$ such that

{\sum_{i \in X_{i}} : I \subset [m], I \neq \emptyset}

is monochromatic.

Also known as Folkman’s Theorem

Proof. The previous theorem implies this: any $(m, 1, 1)$ -set contains a set of the above desired form. □

Also: what about products? If $c : ℕ \to [k]$ then induce $c^{'} : ℕ \to [k]$ by $c^{'} (n) = c (2^{n})$ .

By the above for $c^{'}$ you get $x_{1}, \dots, x_{n}$ such that $c (\prod_{I \neq 0} 2^{x_{i}})$ is constant.

Question: Can we always fine $x_{1}, \dots, x_{n} \in ℕ$ (when finitely coloured) such that the set

{\sum_{i \in I} x_{i}, \prod_{i \in I} x_{i} \forall I \subseteq [n], I \neq \emptyset}

is monochromatic?

This is very open …even $n = 2$ , i.e. ${x, y, x + y, x y}$ .

Remark.

(1) If you insist on an infinite set ${(x_{i})}_{i \in ℕ}$ , then you can find a bad colouring (Some new results on monochromatic sums and products over the rationals [Hindman, Ivan, Leader]).
(2) If we ask this question over $ℚ$ – true (Alweiss, 2023+).
(3) It is also true that ${x, x + y, x y}$ is partition regular over $ℕ$ (2023, Bowen and someone)

Proposition 2.8. Assuming that:

$A$ has the column property

Then there exists

m, p, c

such that any

(m, p, c)

-set contains a solution to

A y = 0

Proof. Let $C_{1}, \dots, C_{n}$ be the columns of $A$ . Then there exists $B_{1} ⊔ B_{2} ⊔ \dots ⊔ B_{r}$ a partition of $[n]$ such that

\sum_{i \in B_{k}} C_{i} \in {span}_{ℚ} (C_{i} : i \in B_{1} \cup \dots \cup B_{k - 1}) .

For all $k$ , we have

\sum_{i \in B_{k}} C_{i} = \sum_{i \in B_{1} \cup \dots \cup B_{k - 1}} q_{i k} C_{i}

with $q_{i k} \in ℚ$ .

For each $k$ , let

d_{i k} = {\begin{matrix} 0 & if i \notin B_{1} \cup \dots \cup B_{k} \\ 1 & if i \in B_{k} \\ - q_{i k} & if i \in B_{1} \cup \dots \cup B_{k - 1} \end{matrix}

Rewriting the above we get

\sum_{i = 1}^{n} d_{i k} C_{i} = 0

for all $k$ . We will take $m = r$ . Let $x_{1}, \dots, x_{r}$ be some integers. Let $y_{i} = \sum_{k = 1}^{r} d_{i k} x_{k}$ .

Claim ${(y_{1}, \dots, y_{n})}^{⊤}$ is a solution, i.e. $\sum_{i = 1}^{n} y_{i} C_{i} = 0$ . Indeed:

\begin{array}{l} \sum_{i = 1}^{n} y_{i} C_{i} & = \sum_{i - 1}^{n} \sum_{k = 1}^{r} d_{i k} x_{k} C_{i} \\ = \sum_{k = 1}^{r} \sum_{i = 1}^{n} d_{i k} x_{k} C_{i} \\ = \sum_{k = 1}^{r} x_{k} (\underset{= 0}{\underset{⏟}{\sum_{i = 1}^{n} d_{i k} C_{i}}}) \\ = 0 \end{array}

Look at $y_{i} = \sum_{k = 1}^{n} d_{i k} x_{k}$ . Have $d_{i k} \in ℚ$ . Let $c$ be the common denominator of all the $q_{i k}$ s. Then

c y_{i} = \sum_{k = 1}^{n} \underset{\in ℕ}{\underset{⏟}{c d_{i k}}} x_{k}

Also have that $c y$ is a solution. Our $c$ (for the $(r, p, c)$ -set) is indeed the common denominator of the $q_{i k}$ , and $p = c \cdot \max | numerators |$ . □

Proof of Rado’s Theorem. Want to prove $A$ is partition regular if and only if it has the column property.

If $A$ is partition regular, then by Proposition 2.5, it has the column property.

For the other direction, let $\tilde{c}$ be a finite colouring of $ℕ$ . Also, since $A$ has column property there exists $m, p, c$ such that $A x = 0$ solutions in any $(m, p, c)$ -set. By Theorem 2.6 there exists a monochromatic $(m, p, c)$ -set with respect to $\tilde{c}$ . But this gives a monochromatic solution to $A x = 0$ . □

Remark. From the proof, we get that if $A$ is partition regular for the “ $mod p$ ” (right-most position in base $p$ ) colourings then in fact $A$ is partition regular for any colouring. There is no direct proof of this (i.e. that does not go via the Rado’s Theorem proof).

Theorem 2.9 (Consistency Theorem). Assuming that:

$A$ and $B$ two matrices that are partition regular

Then

(\begin{matrix} A & 0 \\ 0 & B \end{matrix})

is partition regular.

Proof. Trivial check of column property. □

This says that if you can solve $A x = 0$ monochromatically and you can solve $B x = 0$ monochromatically, then there exists $y_{1}, y_{2}$ of the same colour such that $A y_{1} = 0$ , $B y_{2} = 0$ .

Remark. You can show this by hand (but much harder).

Theorem 2.10. Assuming that:

$ℕ$ finitely coloured

Then a colour class contains solutions to all partition regular equations.

Proof. $ℕ = C_{1} ⊔ C_{2} ⊔ \dots ⊔ C_{k}$ . Assume for all $C_{i}$ that there exists $A_{i}$ that is partition regular, but has no solution in $C_{i}$ . Look at

(\begin{matrix} A_{1} & 0 & \dots & 0 \\ 0 & A_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & A_{k} \end{matrix}) .

This is partition regular too, hence it has a monochromatic solution of colour say $C_{t}$ . Then $A_{t}$ has a solution in $C_{t}$ , contradiction. □

Rado’s conjecture (1933)

Definition. $D \subseteq ℕ$ is partition regular if it contains solutions to all partition regular equations.

Rado conjectured that if $D = D_{1} ⊔ D_{2} ⊔ \dots ⊔ D_{k}$ , then one is also partition regular.

Proved in 1973 by Deuber – introduced $(m, p, c)$ -sets. Showed that $D$ is partition regular if and only if it contains an $(m, p, c)$ -set for all $m, p, c$ .

He then showed that given $m, p, c, k$ , there exists $n, q, d$ such that whenever an $(n, q, d)$ -set is $k$ -coloured, there exists a monochromatic $(m, p, c)$ -set (this indeed solved the conjecture).

2.2 Ultrafilters

Aim:

Theorem 2.11 (Hindman’s Theorem). Assuming that:

$ℕ$ is finitely coloured

Then there exists infinitely many

{(x_{n})}_{n \geq 1}

such that

FS (X_{1}) : = {\sum_{i \in I} x_{i} : \emptyset \neq I \subseteq ℕ, I finite}

is monochromatic.

This is the first infinite partition regular system in the course.

Definition (Filter). A filter is a non-empty collection $F$ of subsets of $ℕ$ satisfying:

(a) $\emptyset \notin F$ .
(b) If $A \in F$ , $A \subset B$ , then $B \in F$ (‘upset’).
(c) If $A \in F$ , $B \in F$ then $A \cap B \in F$ (closed under finite intersections).

Example.

(1) $F = {A \subseteq ℕ : 1 \in A}$ is a filter.
(2) $F = {A \subseteq ℕ : 1, 2 \in A}$ is a filter.
(3) $F = {A \subseteq ℕ : A^{c} is finite}$ is a filter, called the cofinite filter.
(4) $F = {A \subseteq ℕ : A is infinite}$ . This is not a filter, since the intersection ${odd numbers} \cap {even numbers}$ is $\emptyset$ , which is not in $F$ .
(5) $F = {A \subseteq ℕ : {even numbers} ∖ A is finite}$ is a filter.

Definition (Ultrafilter). An ultrafilter is a maximal filter.

Example.

1. $U = {A \subseteq ℕ : x \in A}$ , $B \notin U$ , then $B^{c}$ will contain $x$ , so $B^{c} \in U$ , but $B^{c} \cap B = \emptyset$ so we cannot extend $U$ by adding $B$ to it. So $U$ is maximal. This is called the principal filter at $x$ .
2. In the examples above: (1) is an ultrafilter, (2) is not as (1) extends it, (3) is not as (5) extends it, and (5) is not as $F^{'} = {A \subseteq ℕ : {multiples of 4} ∖ A is finite}$ extends it.

Proposition 2.12. $U$ is an ultrafilter if and only if for all $A \subseteq ℕ$ , either $A \in U$ or $A^{c}$ is in $U$ .

Proof.

$\Leftarrow$ If I try to extend $U$ by adding in some $A \notin U$ , then since $A^{c} \in U$ , we would also have to have $A \cap A^{c} \in U$ , which violated one of the properties of being a filter.
$\Rightarrow$ Suppose $U$ is an ultrafilter and there exists $A$ such that $A, A^{c}$ are not in $U$ .
By maximality, if $A$ is not in $U$ then there exists $B \in U$ such that $A \cap B = \emptyset$ . Indeed, suppose not. Then
$F^{'} = {S : S \supseteq A \cap B for some B \in U}$

extends it (the only way this can fail to be a filter is if $\emptyset \in F^{'}$ , which would require a $B$ such that $A \cap B = \emptyset$ ).

Then $B \subseteq A^{c}$ , so $A^{c} \in U$ , contradicting the initial assumption. □

Remark. If $U$ is an ultrafilter and $A \in U$ , $A = B \cup C$ . Then either $B$ or $C$ is in $U$ . Indeed, suppost not. Then $B^{c}, C^{c} \in U$ , hence $B^{c} \cap C^{c} \in U$ , i.e. $B^{c} \cap C^{c} = {(B \cup C)}^{c}$ is in $U$ . Hence $A \cap A^{c} = \emptyset \in U$ , a contradiction.

Proposition 2.13. Assuming that:

$F$ a filter

Then there exists an ultrafilter

U

extending

F^{'}

Proof. By Zorn’s lemma, it is enough to show that any chain of filters extending $F$ has an upper bound.

Let ${(F_{i})}_{i \in I}$ be a chain of filters containing $F$ , i.e. for all $i \neq j$ either $F_{i} \subseteq F_{j}$ or $F_{j} \subseteq F_{i}$ . Let $F = ⋃_{i \in I} F_{i}$ . Need to show $F$ is a filter:

(1) $\emptyset \notin F$ since $\emptyset \notin F_{i}$ for each $i$ .
(2) If $A \in F$ and $A \subseteq B$ then $A \in F_{i}$ for some $i$ , and then we have $B \in F_{i}$ for this same $i$ (as $F_{i}$ is a filter), so $B \in F$ .
(3) If $A, B \in F$ then say $A \in F_{i}$ , $B \in F_{j}$ . Since $(F_{i})$ is a chain, we can suppose without loss of generality that $F_{i} \subseteq F_{j}$ . Then $A, B \in F_{j}$ , so $A \cap B \in F_{j} \subseteq F$ , so $A \cap B \in F$ .

and also clearly $F$ extends $F$ . So $F$ is an upper bound. □

Remark.

(1) Any ultrafilter that extends the cofinite filter cannot be principal. Suppose $F$ is the cofinite filter and $U$ is a filter extending it. If $U = U_{x}$ then ${x}^{c} \in F \subseteq U$ but we also have ${x} \in U$ , contradiction.
(2) If $U$ is non-principal, then it must extend the cofinite filter. If $U$ were to contain a finite set $A = {x_{1}} \cup \dots \cup {x_{i}}$ , so there exists $i$ such that ${x_{i}} \in U$ (contradiction). If $A$ is a set in the cofinite filter, then $A^{c}$ is finite, so $A^{c} \notin U$ , hence $A \in U$ .
(3) The Axiom of Choice is absolutely needed for the existence of non-principal ultrafilters.

Definition ( $b e t a N$ ). The set of ultrafilters on $ℕ$ is called $β ℕ$ . We define a topology on $β ℕ$ as the one induced by the following base of open sets

C_{A} : = {U : A \in U} .

We can see that $⋃_{A} C_{A} = β ℕ$ and $C_{A} \cap C_{B} = C_{A \cap B}$ because $A \cap B \in U$ if and only if $A, B \in U$ .

Open sets are $⋃_{i \in I} C_{A_{i}}$ .

Closed sets are $⋂_{i \in I} C_{A_{i}}$ (using the fact that ${(⋃_{i \in I} C_{A_{i}})}^{c} = ⋂_{i \in I} C_{A_{i}}^{c} = ⋂_{i \in I} C_{A_{i}^{c}}$ ).

Remark.

(1) $β ℕ ∖ C_{A} = C_{A^{c}}$ .
(2) We can view $ℕ$ embedded in $β ℕ$ by identifying $n \in ℕ$ with the principal ultrafilter at $n$ , i.e. $ñ = {A : n \in A}$ , ${\tilde{1}, \tilde{2}, \dots} \leftrightarrow ℕ$ .
Each point in $ℕ$ is isolated because $C_{{n}} = ñ$ . Under this, $ℕ$ is dense in $β ℕ$ : for $C_{A}$ an open set and $n \in A$ we have $ñ \in C_{A}$ .

Proposition 2.14. $β ℕ$ is a compact Hausdorff space.

Proof. $β ℕ$ is Hausdorff: Let $U \neq V$ be two ultrafilters. Then there exists $A \in U$ such that $A \notin V$ . Then $U \in C_{A}$ (and $C_{A}$ is open), and $A^{c} \in V$ , hence $V \in C_{A^{c}}$ (and $C_{A^{c}}$ is open). Note $C_{A} \cap C_{A^{c}} = \emptyset$ . So indeed $β ℕ$ is Hausdorff.

$β ℕ$ is compact: want to show that every open cover has a finite subcover. This is equivalent to showing that if a collection of closed sets has the property that no finite subset covers $β ℕ$ , then the whole collection doesn’t cover $β ℕ$ . This is equivalent to showing that if you have a collection of closed sets such that they have the finite intersection property (for any $J \subset I$ finite, $⋂_{i \in J} F_{i} \neq \emptyset$ ), then their intersection is non-empty.

Further, in the first sentence we can without loss of generality that the open sets are basis sets (i.e. of the form $C_{A}$ ), and carrying this forward tells us that we may assume that the closed sets in the last sentence are of the form $C_{A}^{c}$ , or equivalently, of the form $C_{A}$ .

We are given some closed, non-empty sets in $β ℕ$ . Without loss of generality, they are all $C_{A}$ for some $A \neq \emptyset$ . Suppose ${(C_{A_{i}})}_{i \in I}$ with the finite intersection property. First note $C_{A_{i_{1}}} \cap C_{A_{i_{2}}} \cap \dots \cap C_{A_{i_{k}}} = C_{A_{i_{1}} \cap \dots \cap A_{i_{k}}} \neq \emptyset$ , hence $A_{i_{1}} \cap \dots \cap A_{i_{k}}$ .

So let $F = {A : A \supset A_{i_{1}} \cap A_{i_{2}} \cap \dots \cap A_{i_{k}} for some {(A_{i_{j}})}_{j = 1}^{n}}$ . $F$ is a filter because:

(1) $\emptyset \notin F$
(2) $B \supset A ⟹ B \in F$
(3) If $A \supset ⋂ A_{i_{j}}$ , $B \supset ⋂ A_{k_{j}}$ , then $A \cap B \supset ⋂ A_{i_{j}} \cap ⋂ A_{k_{j}}$ hence $A \cap B \in F$ .

Let $U$ be an ultrafilter extending $F$ . Note: $\forall A_{i} \in U$ if and only if $U \in C_{A_{i}} \forall i$ . Hence $U \in ⋂ A_{A_{i}} ⟹ ⋂ C_{A_{i}} \neq \emptyset$ . Thus $β ℕ$ is compact. □

Remark.

(1) $β ℕ$ can be viewed as a subset $P (ℕ) \to {0, 1}$ or a subset of ${0, 1}^{P (ℕ)}$ . The topology on $β ℕ$ comes from restricting the product topology on ${0, 1}^{P (ℕ)}$ and also $β ℕ$ is a closed subset of ${0, 1}^{P (ℕ)}$ , hence it is compact by Tychonoff’s theorem.
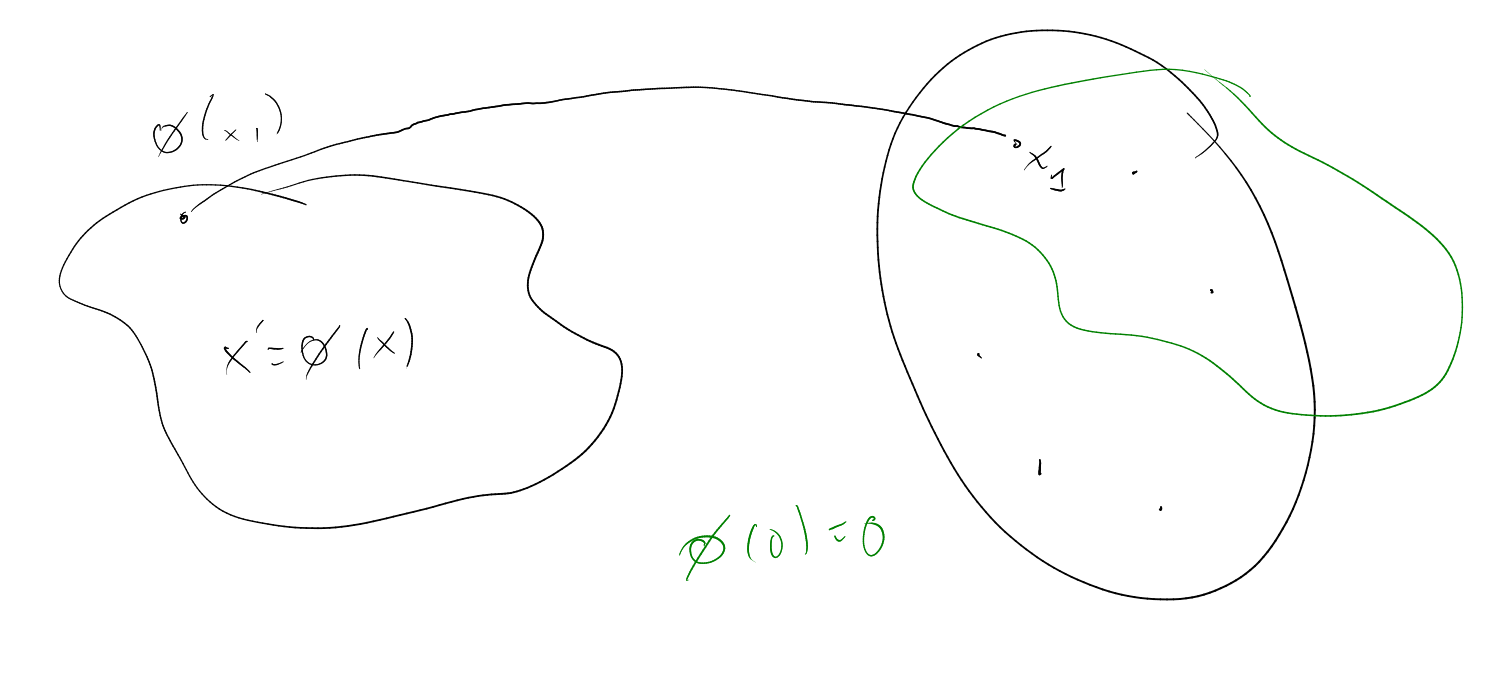
(2) $β ℕ$ is the biggest compact Hausdorff space in which $ℕ$ is dense. In other words, if $X$ is compact and Hausdorff and $f : ℕ \to X$ , there exists a unique $\tilde{f}$ continuous that extends $f$ , i.e. $\tilde{f} : β ℕ \to X$ makes the diagram
commute.
(3) $β ℕ$ is called the Stone-Cěch Compactification of $ℕ$ .

Notation. Let $p$ be a statement and $U$ an ultrafilter. We write

\forall_{U} x, p (x)

to mean ${x : p (x)} \in U$ (“ $p (x)$ holds for ( $U$ -)most $x$ ”).

Example.

(1) If $U$ is principal, then $U = ñ$ so $\forall_{U} x, p (x) ⟺ p (n)$ .
(2) If $U$ is not principal then let’s consider $\forall_{U} x, (4 < x)$ . This says ${x : x > 4} \in U$ . If not true, then ${x : x > 4}^{c} \in U$ , i.e. ${1, 2, 3, 4} \in U$ . Then ${1} \cup {2} \cup {3} \cup {4} \in U$ hence for some $1 \leq i \leq 4$ , ${i} \in U$ , so $U$ is principal, contradiction.

Proposition 2.15. Assuming that:

$U$ an ultrafilter
$p, q$ statements

Then

(i) $\forall_{U} x, (p (x) and q (x))$ if and only if $\forall_{U} x, p (x)$ and $\forall_{U} x, q (x)$
(ii) $\forall_{U} x, (p (x) or q (x))$ if and only if $\forall_{U} x, p (x)$ or $\forall_{U} x, q (x)$
(iii) $\forall_{U} x, p (x)$ is false if and only if $\forall_{U} x, \neg p (x)$

Proof. Let $A = {x : p (x)}$ , $B = {x : q (x)}$ .

(i) $A \cap B \in U$ if and only if $A \in U$ and $B \in U$
(ii) $A \cup B \in U$ if and only if $A \in U$ or $B \in U$
(iii) $A \notin U$ if and only if $A^{c} \in U$ □

Warning. $\forall_{U} x, \forall_{V} y, p (x, y)$ is not necessarily the same as $\forall_{V} y, \forall_{U} x, p (x, y)$ (there is even a counterexample in the case $U = V$ !).

Example. Let $U$ be a non-principal ultrafilter. Let $p (x, y) = x < y$ . Then:

$\forall_{U} x \forall_{U} y, x < y$ is true (since $\forall_{U} y, x < y$ is always true)
$\forall_{U} y \forall_{U} x, x < y$ is false (since $\forall_{U} x, x < y$ is always false)

Moral. Don’t swap quantifiers!!

Cool fact: we can “add” ultrafilters.

Definition (Addition of ultrafilters). Let $U, V$ be ultrafilters. Then we define

U + V = {A \subseteq ℕ : \forall_{U} x, \forall_{V} y, x + y \in A} .

Example. $\tilde{m} + ñ + \tilde{m + n}$ .

Proof that $U + V$ is a filter:

(1) $\emptyset \notin U + V$
(2) If $A \in U + V$ and $B \supset A$ then trivially $B \in U + V$
(3) Intersections: if $A \in U + V$ and $B \in U + V$ , then:
- $\forall_{U} x, \forall_{V} y, x + y \in A$
- $\forall_{U} x, \forall_{V} y, x + y \in B$
hence by Proposition 2.15(i) applied twice, we have $\forall_{U} x, \forall_{U} y, x + y \in A \cap B$ .

Hence $U + V$ is a filter.

Now check that it is an ultrafilter:

Suppose $A \notin U + V$ , i.e. $\forall_{U} x, \forall_{V} y, x + y \in A$ is false. By Proposition 2.15(iii) applied twice, this is equivalent to $\forall_{U} x, \forall_{V} y, x + y \in A^{c}$ . Hence $A^{c} \in U + V$ .

So $U + V$ is indeed an ultrafilter.

Remark. The addition of ultrafilters is associative, i.e.

U + (V + W) = (U + V) + W .

To show this, we claim $A \in LHS$ if and only if

\forall_{U} x, \forall_{V} y, \forall_{W} z, x + y + z \in A .

By similar reasoning, one can also show $A \in RHS$ if and only if the above holds, hence $A \in LHS$ if and only if $A \in RHS$ , which establishes the desired equality.

Let $A \in U + (V + W)$ . So $\forall_{U} x, (\forall_{V + W} y, x + y \in A)$ . Let $B_{x} = {y : x + y \in A}$ . TODO

Last piece of the puzzle: $+$ is left continuous: we show that $U \mapsto U + V$ is continuous (for any fixed $V$ ).

Proof. Note $U + V \in C_{A}$ (for some $A$ ) if and only if $A \in U + V$ , which happens if and only if $\forall_{U} x, \forall_{V} y, x + y \in A$ . This is equivalent to saying

{x : \forall_{V}, x + y \in A} \in U,

which is equivalent to $U \in C_{{x : \forall_{V} y, x + y \in A}}$ , so the pre-image is open. □

Recall: $β ℕ$ is compact Hausdorff, with $ℕ$ a dense subset, $+$ is left continuous, associative, and $β ℕ$ is non-empty.

Goal: want $U$ such that $U + U = U$ , i.e. idempotent.

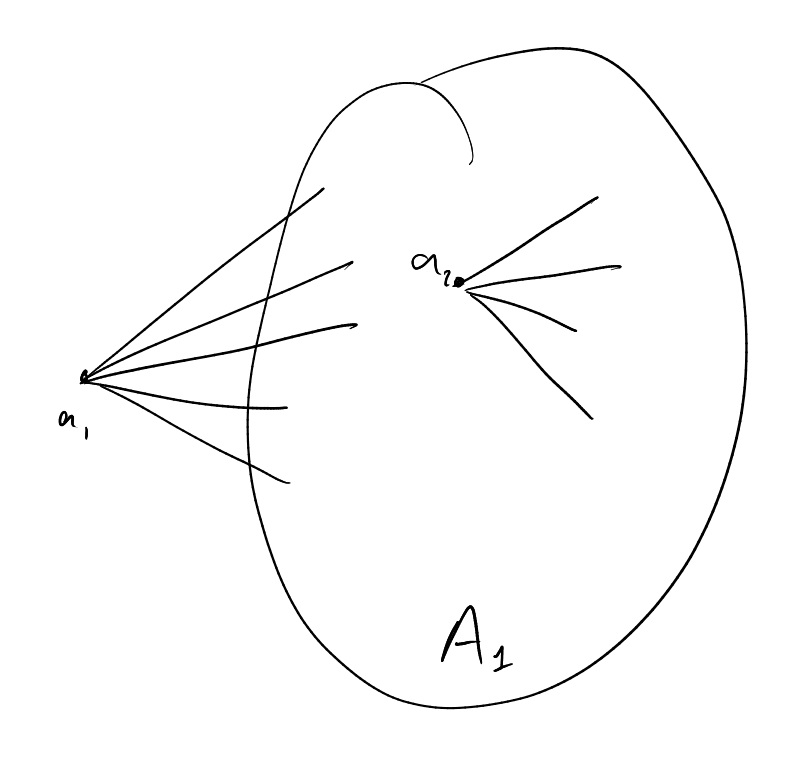
Proposition 2.16 (Idempotent lemma). There exists $U \in β ℕ$ such that $U = U + U$ .

Proof. (Warning: we will use Zorn’s lemma :O)

Start with $M \subseteq β ℕ$ such that $M + M : = {x + y : x, y \in M} \subseteq M$ . Seek $M \subseteq β ℕ$ , non-empty, compact and minimal with the property that $M + M \subseteq M$ (hope to show $M$ is a singleton).

Proof of existence: there exists such a set, namely $β ℕ$ itself. Look at all such $M$ – this set is not empty. By Zorn’s lemma, it is enough to show that if ${(M_{i})}_{i \in I}$ is a collection of such sets that is also a chain, then $M = ⋂_{i \in I} M_{i}$ has this property also ( $M + M \subseteq M$ , $M$ is compact).

Compact: We are in a compact Hausdorff space, so a subspace is compact if and only if it is closed. Since the $M_{i}$ are closed we have that $M$ is closed, hence $M$ is compact.

Why $M + M \subseteq M$ ? Let $x, y \in M$ , $x, y \in M_{i}$ for all $i$ . Then $x + y \in M_{i} + M_{i} \subseteq M_{i}$ for all $i$ , hence $x + y \in M_{i}$ for all $i$ , hence $x + y \in M$ . So $M + M \subseteq M$ .

Also $M$ is non-empty: ${(M_{i})}_{i \in M}$ have the finite intersection property (as they are a chain). Since they are closed, we get that the intersection is non-empty.

Therefore, by Zorn’s lemma, there exists a minimal $M$ , which is non-empty, compact such that $M + M \subseteq M$ .

Pick $x \in M$ . Look at $M + x$ and we want to show that this is $M$ .

Claim: $M + x = M$ .

Proof: $M + x \subseteq M + M \subseteq M$ . Check:

non-empty
compact, as continuous image ( $∙ + x$ ) of a compact set
$(M + x) + (M + x) = (M + x + M) + x \subseteq M + x$

So by minimality $M + x = M$ .

In particular, there exists $y \in M$ such that $y + x = x$ . Consider $T = {y \in M : y + x = x}$ .

Claim: $T = M$ . Since $T \subseteq M$ , it’s enough to show (by minimality) that $T$ is compact, non-empty and $T + T \subseteq T$ . Indeed:

non-empty: $y \in T$
$T$ compact as $T$ is the pre-image of a singleton (which is compact hence closed), thus closed, thus compact.
for $T + T \subseteq T$ : $y, z \in T$ , $y + x = x$ , $z + x = x$ so $y + z + x = y + x = x$ hence $y + z \in T$ . So $T + T \subseteq T$ .

By minimality, $T = M$ .

So ${y : y + x = x} = M$ , hence $x + x = x$ . □

Remark. $M = {x}$ .

Remark.

(1) The finite subgroup question: can we find a non-trivial subgroup of $β ℕ$ ? For example, $U$ , $U + U \neq U$ , $U + U + U = U$ ? Solved by Zeleyum (1996) – No!
(2) Can an ultrafilter “absorb” another ultrafilter? That is, $U \neq V$ such that all $U + U$ , $U + V$ , $V + U$ , $V + V$ are equal to $V$ ? Totally open (until it was show that the answer is yes)!

Proof of Hindman’s Theorem. (If $ℕ$ is finitely coloured, there exists ${(x_{n})}_{n = 1}^{\infty}$ such that $FS (x_{1}, x_{2}, \dots)$ is monochromatic).

Let $A_{1}, A_{2}, \dots, A_{k}$ be the colour classes ( $A_{1} ⊔ A_{2} ⊔ \dots ⊔ A_{k} = ℕ$ ) and $U$ an idempotent ultrafilter.

Claim: $A_{i} \in U$ for some $i$ (this is because ultrafilters are prime: whenever we have a finite union lying in the ultrafilter we have at least one of the components lying in the ultrafilter, else have $A_{i}^{c} \in U$ for each $i$ , hence $A_{1}^{c} \cap \dots \cap A_{k}^{c} \in U$ , but this is ${(A_{1} \cup \dots \cup A_{k})}^{c}$ , contradicting the fact that $A_{1} \cup \dots \cup A_{k} \in U$ ).

Let $A = A_{i} \in U$ . Therefore we have $\forall_{U} y, y \in A$ . Then:

(1) $\forall_{U} x, \forall_{U} y, y \in A$
(2) $\forall_{U} x, \forall_{U} y, x \in A$
(3) $A \in U + U = U$ gives that $\forall_{U} x, \forall_{U} y, x + y \in A$ .

Then (1) and (2) and (3) give:

\forall_{U} x, \forall_{U} y, FS (x, y) \subseteq A .

Now fix $x_{1} \in A$ such that

\forall_{U} y, FS (x_{1} x) \subseteq A .

Assume we have found $x_{1}, \dots, x_{n}$ such that

\begin{array}{l} \forall_{U} y, FS (x_{1}, \dots, x_{n}, y) & \subseteq A \\ \underset{= : B}{\underset{⏟}{{y : FS (x_{1}, \dots, x_{n}, y) \subseteq A}}} & \in U = U + U \end{array}

Then have $\forall_{U} x, \forall_{U} y, x + y \in B$ .

(1) $\forall_{U} x, \forall_{U} y, FS (x_{1}, \dots, x_{n}, y) \subseteq A$
(2) $\forall_{U} x, \forall_{U} y, FS (x_{1}, \dots, x_{n}, x) \subseteq A$
(3) $\forall_{U} x, \forall_{U} y, FS (x_{1}, \dots, x_{n}, y) \subseteq A$ .

Then (1), (2) and (3) give:

\forall_{U} x, \forall_{U} y, FS (x_{1}, \dots, x_{n}, y) \subseteq A .

Thus fix $x_{n + 1} ≫ x_{n}$ . Have $\forall_{U} y, FS (x_{1}, \dots, x_{n}, y) \subseteq A$ . Then done by induction. □

Remark.

(1) Very few other infinite partition regular equations are known. In particular, there does not exist a “Rado-type” theorem of iff.
(2) The consistency theorem no longer holds.
${FS}_{12} (x_{1}, x_{2}, \dots) = . c b \sum_{i \in I} x_{i} + 2 \sum_{i \in J} x_{i}, \max I < \min J$

is partition regular (special case of Milliken-Taylor theorem). It was shown in 1995 that ${F S}_{12} (x_{1}, x_{2}, \dots)$ and $FS (x_{1}, x_{2}, \dots)$ are incompatible.
(3) Trivially from Hindman, ${x_{n}}_{n = 1}^{\infty} \cup {x_{i} + x_{i}}$ is partition regular. Any proof of this without Hindman? Not known!

3 Euclidean Ramsey

Launched in 1970 by Erdős, Graham, Montgomery, Rothchild, Spencer and Straus.

Here we want actual copies of some objects.

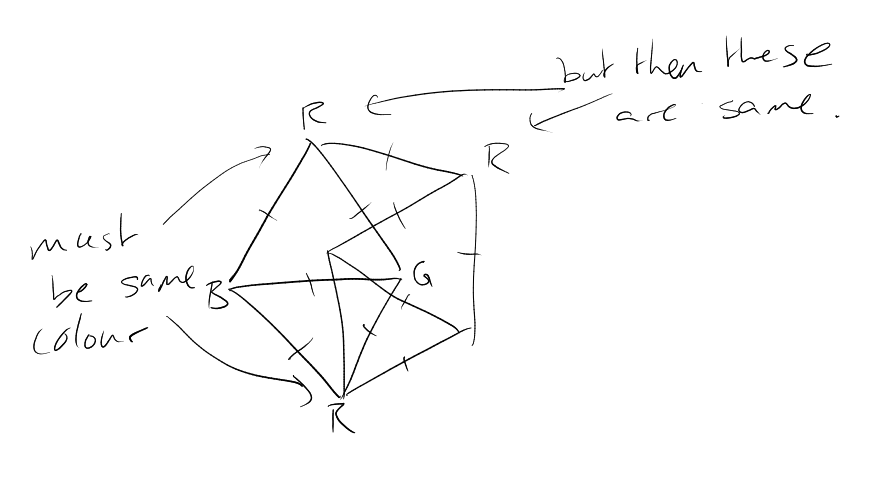
Colourings of $ℝ^{n}$ .

Let us $2$ -colour $ℝ^{2}$ . Then have 2 points of distance $1$ of same colour (consider equilateral triangle of side length $1$ ).

If we $3$ -colour $ℝ^{3}$ , we can also get 2 points of distance $1$ , by considering a regular tetrahedron of side length $1$ .

In general, if we $k$ -colour $ℝ^{k}$ , then by looking at the unit regular simplex $(k + 1)$ , then any $2$ have distance $1$ between them, so we get 2 points having the same colour and being unit distance apart.

Definition (Isometric copy). We say $X^{'}$ is an isometric copy of $X$ if there exists $ϕ : X \to X^{'}$ bijection such that $d (x, y) = d (ϕ (x), ϕ (y))$ .

Definition. We say that a set $X$ (finite) is Ramsey (Euclidean Ramsey) if for all $k$ there exists a finite set $S \subseteq ℝ^{n}$ ( $n$ could be very big) such that whenever $S$ is $k$ -coloured, there exists a monochromatic copy of $X$ .

Example.

(1) ${0, 1}$ is Ramsey: for $k$ -colours, take a $k$ -dimensional unit simplex.
(2) Unit equilateral triangle is Ramsey: for $k$ -colours, can take $2 k$ -dimensional unit simplex.
(3) Similarly have that any ${0, a}$ is Ramsey.
(4) Similarly any regular simplex is Ramsey.

Remark.

(1) If $X$ is infinite, then can build a $2$ -colouring of $ℝ^{n}$ with no monochromatic $X$ (exercise).
(2) We took for $k$ -colours $S$ to be in $ℝ^{k}$ . Can we do better? For ${0, 1}$ , can we do it in $ℝ$ ? Colour $x \mapsto ⌊ x ⌋ mod 2$ . Need $2$ dimensions or higher.
What about ${0, 1}$ ? Can we do it in $ℝ^{2}$ ? Yes we can:

This shows $χ (ℝ^{2}) \geq 4$ (max $χ (G)$ where $G$ is a graph on $ℝ^{2}$ iwth $x \sim y$ if and only if $d (x, y) = 1$ ).

Up until 1990, $4 \leq χ (ℝ^{2}) \leq 7$ (by using hexagonal colouring idea).

De Grey – 2018: showed $χ (ℝ^{2}) \leq 5$ using a graph on $\approx 1500$ vertices. Uses nice ideas and computer assistance.

In general, $1 . 1^{n} \leq χ (ℝ^{n}) \leq 3^{n}$ . Lower bound is hard – by Frankl-Wilson. Upper bound is by a type of hexagonal colouring, by Posy.

Proposition 3.1. $X$ is Euclidean Ramsey if and only if for all $k$ , there exists $n$ such that whenever $ℝ^{n}$ is $k$ -coloured, there exists a monochromatic copy of $X$ .

Proof.

$\Rightarrow$ If $X$ is Euclidean Ramsey then take $S$ finite in $ℝ^{n}$ (for $k$ -colours).
$\Leftarrow$ We know that for all $k$ -colourings of $ℝ^{n}$ , there exists a monochromatic copy of $X$ (by compactness). Suppose not. Therefore, for any set $S$ finite in $ℝ^{n}$ , there exists a bad colouring (i.e. not a copy of $X$ monochromatic). Space of all $k$ -colourings is ${[k]}^{ℝ^{n}}$ , which is compact by Tychonoff. Let
$C_{X^{'}} = {colourings that do not make X monochromatic} .$

This is a closed set. Let ${C_{X^{'}}}_{X^{'} a copy of X}$ . It has the finite intersection property, because any finite $S$ has a bad $k$ -colouring. Hence the intersection of all $C_{X^{'}}$ is non-empty. Hence there exists a colouring of $ℝ^{m}$ with no monochromatic $X$ , contradiction. □

How can we generate Ramsey sets?

Lemma 3.2. Assuming that:

$X \subset ℝ^{n}$ Ramsey
$Y \subset ℝ^{m}$ Ramsey

Then

X \times Y \subset ℝ^{n + m}

is also Ramsey.

Remark.

${0, a}$ is Ramsey, and so is ${0, b}$ . So $a \times b$ rectangles are Ramsey. In particular, any right angled triangle is Ramsey.

By considering ${0, a} \times {0, b} \times {0, c}$ , we can acute angled triangles:

Proof. Let $k$ be a colouring of $S \times T$ , where $S$ is $k$ -Ramsey for $X$ and $T$ is $k^{| S |}$ -Ramsey for $T$ .

We $k^{| S |}$ -colour $T$ as follows:

c^{″} (t) = (c (s_{1}, t), c (s_{2}, t), \dots, c (s_{| S |}, t)) .

By choice of $T$ , there exists a monochromatic $Y^{'}$ (copy of $Y$ ) with respect to $c^{'}$ , i.e. $c (s, y) = c (s, y^{'})$ for all $y, y^{'} \in Y$ and any $s \in S$ .

Now $k$ -colour $S$ via $c^{″} (s) = c^{″} (s, y)$ for some $y \in Y^{'}$ (which is well-defined by the above). By the choice of $X$ , there exists monochromatic $X^{'}$ with respect to $c^{″}$ , and hence $X^{'} \times Y^{'}$ is monochromatic with respect to $c$ . □

Homework: Convince yourself that this is a very standard product argument.

Remark.

(1) In general to prove sets are Ramsey we will first embed them into other sets (with ‘cool’ symmetry groups) and show that those sets are Ramsey.
(2) Spoiler:
- Obtuse triangles are Ramsey (twisted prism).
- Any regular $n$ -gon is Ramsey.
- 3D Platonic solids.

Next time: non-Ramsey. (think about ${0, 1, 2}$ ?)

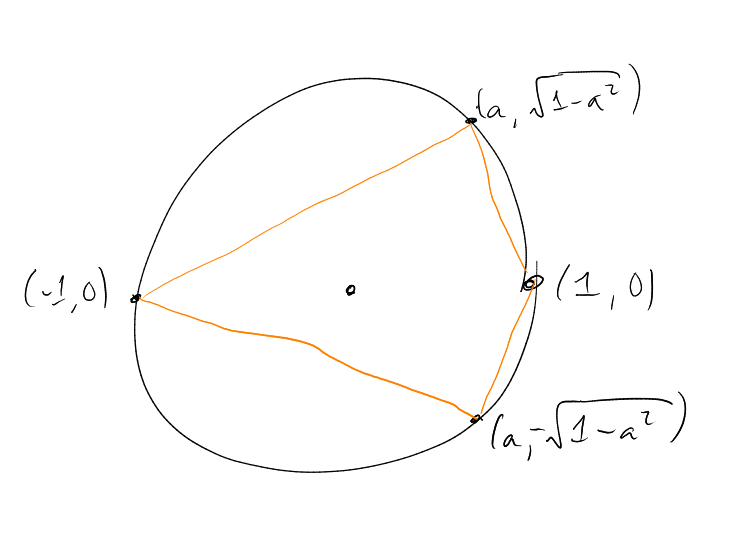
Proposition 3.3. $X = {0, 1, 2}$ is not Ramsey.

Proof. Recall in $ℝ^{n}$ we have

∥ x + y ∥_{2}^{2} + ∥ x - y ∥_{2}^{2} = 2 (∥ x ∥_{2}^{2} + ∥ y ∥_{2}^{2}) .

Every copy of ${0, 1, 2}$ is ${x - y, x, x + y}$ with $∥ y ∥_{2} = 1$ (in any $ℝ^{n}$ ). We have

∥ x + y ∥_{2}^{2} + ∥ x - y ∥_{2}^{2} = 2 ∥ x ∥_{2}^{2} + 2 .

If we can find a colouring of $ℝ_{\geq 0}$ such that there does not exist a monochromatic solution to $a + b = 2 c + 2$ . Then use $c (x) \to ϕ (∥ x ∥_{2}^{2})$ .

We $4$ -colour $ℝ_{\geq 0}$ by $ϕ (x) = ⌊ x ⌋ (m o d 4)$ .

Suppose $a, b, c$ all have colour $n \in {0, 1, 2, 3}$ . Then $a + b = c + 2$ implies

a + b - 2 c = M_{4} + {a} + {b} - 2 {c} = 2

where $M_{4}$ is a multiple of $4$ . This is impossible as $- 2 < {a} + {b} - 2 {c} < 2$ . □

Remark.

(1) For all $n$ , there is a $4$ -colouring of $ℝ^{n}$ that stops every copy of $X = {0, 1, 2}$ from being monochromatic.
(2) Very important in $a + b = 2 c + 2$ , we got this $2$ to not be $0$ .
(3) It will turn out that the property that made ${0, 1, 2}$ not Ramsey is “it does not lie on a sphere”.

Definition (Spherical). A set $X \subseteq ℝ^{n}$ is called spherical if it lies on the surfcace of a sphere.

For example, a triangle, a rectangle, any simplex (non-degenerate).

Definition (Simplex). Let $x_{1}, \dots, x_{d}$ be some points. They form a simplex if $x_{1} - x_{d}, x_{2} - x_{d}, \dots, x_{d - 1} - x_{d}$ are linearly independent. In other words, they do not lie in a $(d - 2)$ -dimensional affine space.

Aim: If $X$ is Ramsey, then $X$ is spherical.

To do so, we will use a “generalised parallelogram law”.

Lemma 3.4. $x_{1}, \dots, x_{d}$ in $ℝ^{n}$ are not spherical if and only if there exists $c_{i} \in ℝ$ , not all $0$ , such that:

(1) $\sum_{i} c_{i} = 0$
(2) $\sum_{i} c_{i} x_{i} = 0$
(3) $\sum_{i} c_{i} ∥ x_{i} ∥_{2}^{2} \neq 0$

In the previous proof, we took $(1, 1, - 2)$ and $2$ being the value in (3).

Proof.

\Rightarrow

x_{1}, \dots, x_{d}

are not spherical. The first two conditions say that

x_{1}, \dots, x_{d}

is not a simplex: so there exists

c_{1}, \dots, c_{d - 1}

(not all

0

) such that

\sum_{i} c_{i} (x_{i} - x_{d}) = 0

\sum_{i = 1}^{N - 1} c_{i} x_{i} + (- c_{1} - c_{2} - \dots - c_{d - 1}) x_{d} = 0

First we note that (1)–(3) are invariant under translation by $v \in ℝ^{n}$ :

$\sum_{i} c_{i} (x_{i} + v) = 0$ since $\sum_{i} c_{i} = 0$
$\sum_{i} c_{i} ∥ x_{i} + v ∥_{2}^{2} = \sum_{i} c_{i} ∥ x_{i} ∥_{2}^{2} + 2 c_{i} (x_{i}, v) + c_{i} ∥ v ∥_{2}^{2} = \sum_{i} c_{i} ∥ x_{i} ∥_{2}^{2} + 2 (\sum_{i} c_{i} x_{i}, v) + ∥ v ∥_{2}^{2} \sum_{i} c_{i} = \sum_{i} c_{i} ∥ x_{i} ∥_{2}^{2}$

Let us look at a minimal subset of $x_{1}, \dots, x_{d}$ that is not spherical. If we can show this for without loss of generality $x_{1}, \dots, x_{k}$ ( $k \leq d$ ) then take $c_{i} = 0$ for all $i \in [k + 1, d]$ . Let ${x_{2}, \dots, x_{k}}$ . This is spherical by minimality. Suppose the sphere radius is $r$ , and centred at $y$ .

By the above, translate the set such that ${x_{2}, \dots, x_{k}}$ is centred at $0$ . Since ${x_{1}, \dots, x_{k}}$ are not spherical, it is not a simplex. Hence there exists $c_{i}$ such that $\sum_{i} c_{i} (x_{i} - x_{k}) = 0$ . Then

c_{1} x_{1} + c_{2} x_{2} + \dots + c_{k - 1} x_{k - 1} + (- c_{1} - c_{2} - \dots - c_{k - 1}) x_{k} = 0 .

Without loss of generality $c_{i} \neq 0$ . This is fine because the same $c_{i}$ ’s work after translations ((1)–(3) is totally invariant under translations). Then

\sum_{i = 1}^{k} c_{i} ∥ x_{i} ∥_{2}^{2} = c_{1} ∥ x_{1} ∥_{2}^{2} + r^{2} (\sum_{i = 2}^{k} c_{i}) \neq 0

as $∥ x_{i} ∥ \neq r$ .

$\Leftarrow$ Suppose there exists $c_{i}$ as in the statement, and assume $(x_{1}, \dots, x_{d})$ are spherical, centred at $r$ , radius $r$ .
Translate the set so that they are centred at the origin (this preserves all conditions and does not vhange the value of $\sum_{I} c_{i} ∥ x_{i} ∥^{2} \neq 0$ ).

Let $∥ x_{i} ∥^{2} = r^{2}$ . Then
$\sum_{i} c_{i} ∥ x_{i} ∥^{2} = r^{2} \sum_{i} c_{i} = 0$

so $(x_{1}, \dots, x_{d})$ are not spherical. □

Corollary 3.5 (Generalised parallelogram law). Let $X = {x_{1}, \dots, x_{n}}$ be non-spherical. Then there exists $c_{1}, \dots, c_{n}$ not all $0$ with $\sum c_{i} = 0$ and there exists $b \neq 0$ such that $\sum_{i} c_{i} ∥ x_{i} ∥^{2} = b$ .

Very important: This is tru for every copy $X^{'}$ of $X$ (with the same $c_{i}$ and $b$ !).

Choosing the $c_{i}$ as in Lemma 3.4. If $ϕ (X)$ is a copy of $X$

then as we have seen we can translate and the $c_{i}$ and $b$ are unaffected, and $ϕ (0) = 0$ .

After that apply $A$ that corresponds to rotation / reflection, and $∥ A x ∥_{2} = ∥ x ∥_{2}$ , so (3) holds.

Theorem 3.6. Assuming that:

$X$ is Ramsey

Then

X

is spherical.

Proof. Suppose $X$ is not spherical. Then there exists $c_{i}$ (not all $0$ ) such that $\sum_{i} ∥ x_{i} ∥^{2} = b$ and $\sum_{i} c_{i} = 0$ .

Also true for any copy of $X^{'}$ .

Going to split $[0, 1)$ into $[0, δ), [δ, 2 δ), \dots$ for small $δ$ . Then colour depending on where $c_{i} ∥ x ∥^{2}$ lies.

Let’s prove that there is a colouring of $ℝ$ such that $\sum_{i = 1}^{n} c_{i} y_{i} = b$ does not have a monochromatic solution. Let $\sum_{i = 1}^{n - 1} c_{i} (y_{i} - y_{n}) = b$ . By rescaling, we may assume $b = \frac{1}{2}$ . Now we split $[0, 1)$ into intervals $[0, δ), [δ, 2 δ), \dots$ where $δ$ is very small. Let

c (y) = (interval where {c_{1} y} is, interval where {c_{2} y} is, \dots) .

A ${(⌊ \frac{1}{δ} ⌋)}^{n - 1}$ -colouring.

Assume $y_{1}, \dots, y_{n - 1}$ monochromatic under $c$ and such that $\sum c_{i} (y_{i} - y_{n}) = \frac{1}{2}$ .

Hence the sum is within $(n - 1) δ$ of an integer, so not $\frac{1}{2}$ , if $δ$ small enough. □

We have showed Ramsey implies spherical.

What about spherical implies Ramsey?

Still an open question (1975).

What is known:

(1) Triangles are Ramsey, simplices are Ramsey, (old stuff). In 1991, Kriz showed that a regular pentagon is Ramsey and that any regular $m$ -gon is Ramsey. His proof is unbelievably clever!

Aim: To show tht $X = {1, 2, \dots, m} =$ a regular $m$ -gon is Ramsey.

Roughly speaking:

(1) First find a copy of $X$ such that $1$ and $2$ are monochromatic.
(2) Use a product argument to get a copy of $X^{N}$ (with $N$ very large), such that the colouring is invariant under $1, 2$ . e.g.
(3) The above plus some clever stuff to find a copy of $X$ on which $1, 2, 3$ is monochromatic.

Definition ( $A$ -invariant). For a finite $A \subseteq X$ , we say that a colouring of $X^{n}$ is $A$ -invariant if it is invariant under chaning the coordinates within $A$ . i.e. for $x = (x_{1}, \dots, x_{n})$ , $x^{'} = (x_{1}^{'}, \dots, x_{n}^{'})$ if $\forall i$ either $x_{i} = x_{i}^{'}$ or $x_{i}, x_{i}^{'} \in A$ implies $c (x^{'}) = c (x)$ .

Proposition 3.7 (Our product argument). Assuming that:

$X \subseteq ℝ^{d}$
$A \subseteq X$
$\forall k, \exists$ a finite $S \subseteq ℝ^{e}$ such that whenever $S$ is $k$ -coloured, there exists a copy of $X$ that is constant on $A$

Then for all

n, k

, there exists

S^{'}

finite such that whenever

S^{'}

k

-coloured there exists a copy of

X^{n}

that is

A

-invariant.

“boosting from $A$ -constant to $A$ -invariant.”

Proof. (Yawn, product argument…)

We will by induction on $n$ (and all $k$ at once).

$n = 1$ is just the assumption.

Suppose true for $n - 1$ . Fix $k$ . Let $S$ be a finite set such that whenever $S$ is $k^{| X |}$ coloured, there exists an $A$ -invariant copy of $X^{n - 1}$ .

$T$ a finite set such that whenever $T$ is $k^{| S |}$ -coloured, there exists a copy of $X$ with $A$ monochromatic.

Claim: $S \times T$ works for $X^{n}$ .

By definition of $T$ , if we look at $c^{'} (s, t) = (c (s_{1}, t), c (s_{2}, t), \dots, c (s_{| S |}, t))$ , a $k^{| S |}$ -colouring. Thus there exists a copy of $X$ with $A$ monochromatic.

This induces a colouring of $S$ as follows: $c^{″} (s) = (c (s, a), c (s, x_{1}), \dots, c (s, x_{| X | - | A |}))$ for some $a \in A$ (note $c (s, a)$ is well-defined). This is a $k^{| X | - | A | + 1}$ -colouring.

Therefore by the choice of $n$ , there exists a copy of $X^{n - 1}$ that is $A$ -invariant.

Then we are done as this copy of $X$ in $T$ is $A$ -invariant. □

Next time:

Theorem 3.8 (Kriz Theorem). Every regular $m$ -gon is Ramsey.

Note. We will show that we can find $(1, 2, \dots, m), (2, 3, \dots, m, 1), (3, 4, \dots, m, 1, 2), \dots, (m, 1, 2, \dots, m - 1)$ monochromatic, which is a copy of $X$ , but scaled by $\sqrt{m}$ (which is fine as $\sqrt{m}$ is constant).

Proof. $X = {1, 2, \dots, m}$ , where the numbers are the names of points.

We find a copy of $\sqrt{m} X$ of the form

(1, 2, \dots, m), (2, 3, \dots, m, 1), (3, 4, \dots, m, 1, 2), \dots (m, 1, 2, \dots, m - 1) .

We will show by induction on $r$ and all $k$ at once that we can find a copy of $X$ with ${1, 2, \dots, r}$ monochromatic.

$r = 1$ is trivial as it is just a point.

$r = 2$ is 2 points at a specified distance (which we showed is Ramsey).

Assume true for $r$ and all $k$ . By Our product argument, there exists $S$ and $N$ such that we have a $X^{N}$ (copy) on which the colouring is ${1, 2, \dots, r}$ -invariant on $X^{N}$ (for any $N$ ). We will choose $N$ to be as big as we want.

The clever bit:

We will colour $(m - 1)$ sets in $[N]$ say $a_{1} < a_{2} < \dots < a_{m - 1}$ as follows.

$c^{'} ({a_{1}, \dots, a_{m + 1}}) = (c (w_{1}), c (w_{2}), \dots, c (w_{r}))$ is a $k^{r}$ colouring of ${[N]}^{(m - 1)}$ .

As $N$ can be taken as big as needed, by Ramsey there exists a $m$ -monochromatic set. By relabeling, we may assume that this set is ${1, 2, \dots, m}$ coordinates.

Now we look at the following:

with this we note that the colour of $y_{i}$ is the same as the colour of $x_{i + 1}$ .

Now look at: $(1, 2, \dots, m)$ , $2, 3, \dots, m, 1)$ , …, $(r + 1, \dots, r, r - 1)$ . monochromatic copy of ${1, 2, \dots, r + 1}$ . They all have the same colour (ignoring this). □

Remark. Same proof works for any cyclic set: i.e. a set ${x_{1}, \dots, x_{n}}$ such that the map $x_{i} \mapsto x_{i + 1}$ (modulo $n$ ) is a symmetry of the set.

Or equivalently, there exists a cyclic transitive symmetry group on $X$ .

Example. Given by rotation $12 0^{\circ}$ and reflection. Generates order $6$ .

This is Ramsey.

The following discussion is non-examinable (until told otherwise).

A soluble group is “built” up from cyclic groups.

Theorem (Kriz). If $X$ hs a soluble, transitive symmetry group, then $X$ is Ramsey.

Rival conjecture to the spherical conjecture (2010, Leader, Russell, Walters):

$X$ is Ramsey if and only if $X$ is subtransitive (subtransitive means that it can be embedded in a transitive set, i.e. it can be embedded in a set that has a transitive isometry group).

Why are they rival?

spherical does not imply sub-transitive.

sub-transitive does imply spherical: let $X$ be sub-transitive. Embed into $Y$ transitive. There exists a unique minimal sphere containing $Y$ , which is preserved by the isometry group.