Ramsey Theory
Lectured by Maria Ivan
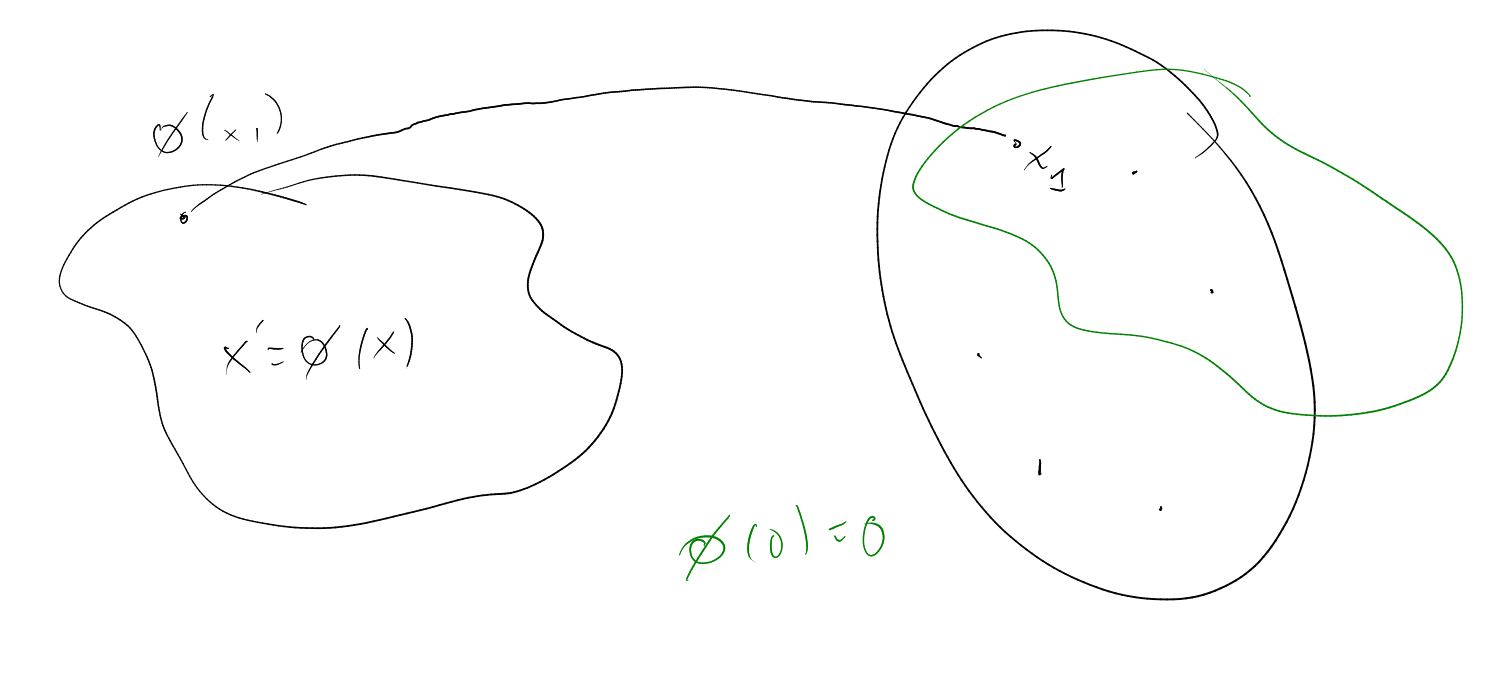
Notation. , for a set , , .
Given a 2-colouring of , are we guaranteed to have an infinite monochromatic set (i.e. , infinite such that the colouring is constant on )?
Example.
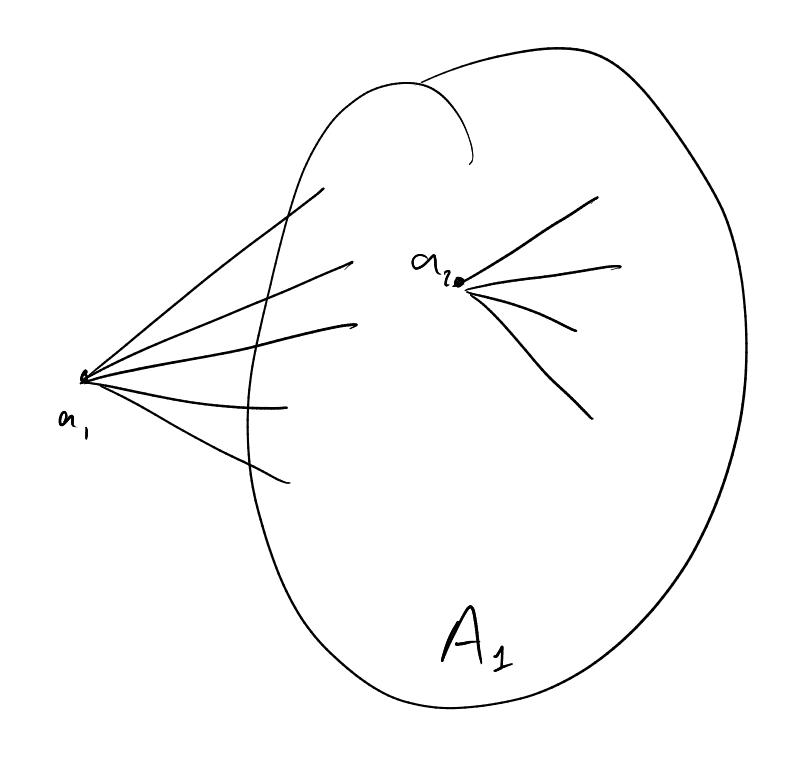
Proof. Pick . Then there exists an infinite set such that for all . Pick and find (infinite) such that for all . Keep on doing this. We end up with and such that for all .
One colour appears infinitely many times . Now note is a monochromatic set. □

Remark.
For example: suppose we write , , and so on. Say is red if there exists such that , and blue otherwise. Then there exist arbitrarily large monochromatic red sets, but no infinite monochromatic red set.
What about with ?
Example. , , red if and only if . Then is monochromatic.
Proof. pigeonhole, is Theorem 1.1. Prove this by induction.
Assume it is true for . Given , we must find (infinite and monochromatic). Pick . Look at the sets of . Define via .
By induction there exists such that is constant on it, say constantly equal to .
Now pick and induce defined by . By induction there exists such that is constant on it, say equal to .
Continuing this, we end up with and sets such that with for all , .
Some colour must appear infinitely many times: say . Check: is monochromatic. □
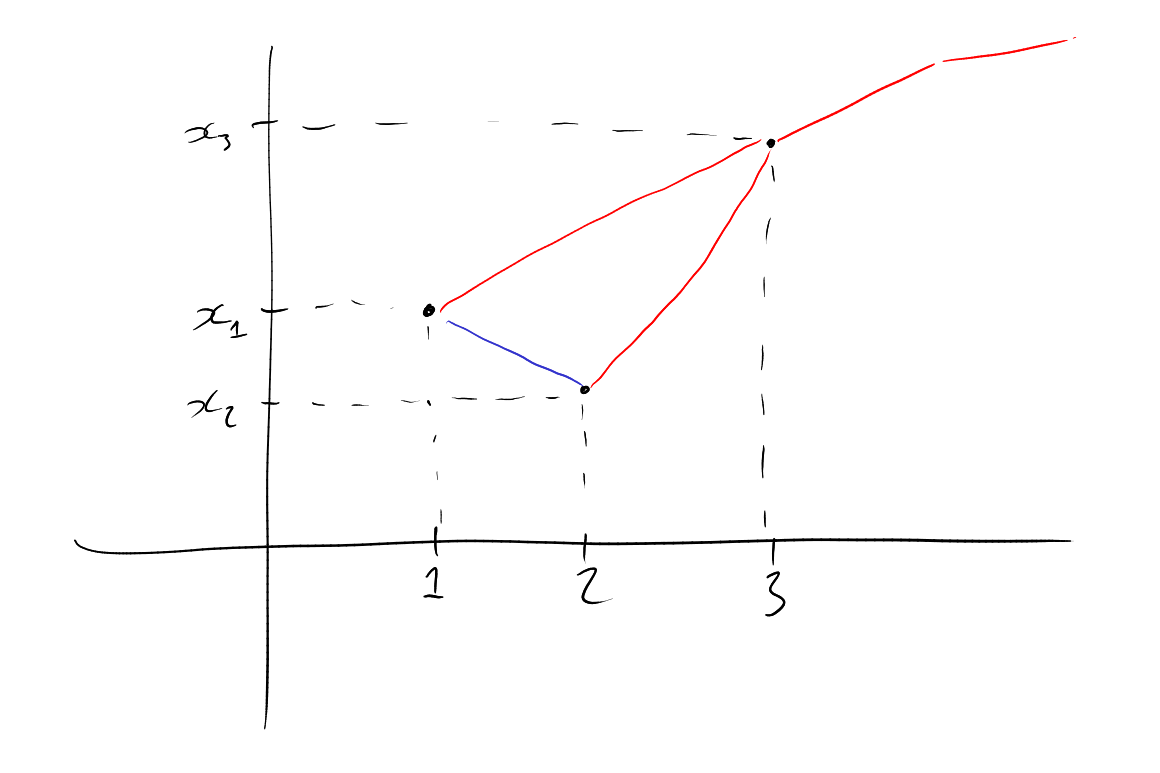
Example. Applications:
Proof. Let the sequence be . Say is red if , and blue otherwise. By Theorem 1.1, we may find monochromatic. If is red, then the sequence is increasing, and if is blue then the sequence is strictly decreasing. □
From Theorem 1.2 we can deduce:
Proof. Suppose not. Then for each we can find with no monochromatic -sets. Note that there are only finitely many ways to -colour . So infinitely many will agree on . Pick such that for all ,
We can do the same on and produce some such that is constant on .
Continuing this, we get . They satisfy:
Finally: colour via , where is any integer . One can see that this is well defined, and gives a contradiction to Theorem 1.2. □
Remark.
What happens if we have with being potentially infinite?
Proof. We colour an element of as follows: We say that it is red if , and blue otherwise.
By Ramsey’s Theorem for -sets, there exists an infinite set that is monochromatic under this colouring.
Let , . Pick (in ) bigger than all . Then hence . Also, , so . So is constant on .
We claim that cannot be green. This is because if is green, let in . Then:
gives us that
gives us that
But using these we get , which contradicts the fact that is blue.
Therefore is purple: for we have .
Next we colour as follows: is orange if , and white otherwise. Again, by Ramsey’s Theorem for -sets we can pick an infinite such that it is monochromatic with respect to this colouring.
We claim that cannot be orange. If it is, then we again consider :
gives that
gives that
Hence , which contradicts the fact that is blue.
Therefore is white. This finally tells us (using earlier working) that given any pair disjoint edges, the colours must be different.
Now, we colour via: yellow if , and pink otherwise. By Ramsey’s Theorem for -sets, there is an infinite that is monochromatic.
We claim that is not yellow. If it is, then given , we have , which contradicts blueness.
Thus for any in , we have .
Finally: we colour with 4 colours, with coloured according to:
turquoise if and
magenta if and
cyan if and
maroon if and
By Ramsey’s Theorem for -sets, there exists a monochromatic set . It cannot be turquoise because contradicts . Then:
magenta implies case (iii)
cyan implies case (iv)
maroon implies (ii), i.e. injective. □
Example. In the previous theorem:
These colourings are call the “canonical colourings” of .
Proof. Exercise. Note that this proof is examinable (because the ideas are exactly the same as those in the previous theorem). □
We will colour .
Aim 1: Whenever we -colour , we find a monochromatic arithmetic progression of length for any .
The abbreviation A.P. can be used to mean “arithmetic progression”, i.e. a sequence of the form .
Aim 2: For any , there exists such that whenever are -coloured, there exists a monochromatic arithmetic progression of length .
This is equivalent to Aim 1, by using a proof by compactness argument like before:
If Aim 2 is not true, then we can find such that infinitely many agree on . Of those infinitely many agree on , etc. Keep going (as before), and then get a colouring of without a monochromatic arithmetic progression of length .
The other direction is easier.
We will show something a bit stronger (because it turns out to be easier): we will prove Aim 2 but with colours.
This is in contrast with the earlier theorems, where the proofs were slightly easier to think about with just 2 colours.
Definition 1.6 (Focused). Let be arithmetic progressions of length . Say
We say that these arithmetic progressions are focused if for all .
If we have a colouring of and are focused arithmetic progressions if each is monochromatic but they all have different colours, then we call them colour-focused.
Example. and are focused at .

Proof. Claim: For any there exists an such that if is -coloured then either:
there exists a monochromatic arithmetic progression of length
there exists colour-focused arithmetic progressions of length
The proof is by induction on .
Base case we can take , since 2 numbers will have the same colour.
Suppose the result is true for and let be an that satisfies the property in the claim.
We will show that works for . Let be a colouring. We will split the ground set into blocks of length . Call the blocks .
If there exists a monochromatic arithmetic progression of length in this colouring, then we are done. So assume not.
By the induction hypothesis, the first half of each has colour-focused arithmetic progressions of length . Because , each block also contains their focus.
For a set , there are exactly ways to -colour it. So there exists two blocks and that are identically coloured.
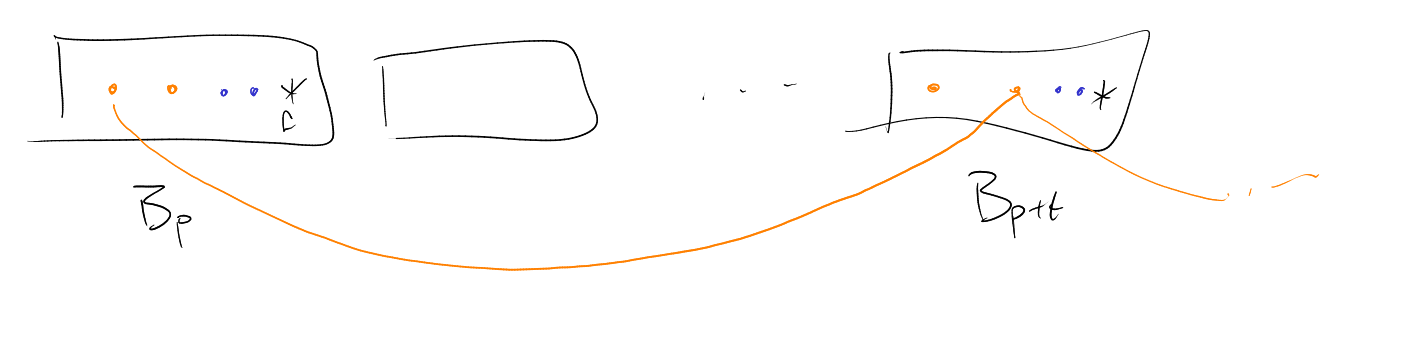
Let be the colour-focused arithmetic progressions in . Then are the corresponding ones in . Let be the focus in , so therefore is the focus in .
Now take for , and . Since , we have . So all of these sequences are focused at .
We know that and are monochromatic by the choice of , . Why colour focused? have different colours by induction hypothesis. Also, because was assumed to have no monochromatic arithmetic progression of length , the colours of must be different to all the colours of the above arithmetic progressions of length . Thus we have colour-focused arithmetic progressions of length in . □
Remark. The idea of looking at all the possible colouring of a set is referred to as the “product argument”.
The Van der Waerden number is the smallest such that whenever is -coloured, there exists a monochromatic arithmetic progression of length .
Proof above claims that for a tower of size . “tower-type bound”.
Theorem 1.8 (Van der Waerden). Assuming that:
Recall that we defined to be the smallest (if it exists) such that whenever is -coloured, there exists a monochromatic arithmetic progression of length .
Proof. This will be by induction on . For any :
is trivial.
is pigeonhole.
is Theorem 1.7.
Assume that this is true for some fixed, but for any . In other words, exists for all .
Claim: For every there exists such that we always have one of the following:
have a monochromatic arithmetic progression of length
colour-focused arithmetic progressions of length
When we are done by looking at the focus. Now we prove the claim. We will prove it by induction on .
For we can take .
Now assume that the result is true for and that there does not exist a monochromatic arithmetic progression of length . We will show that works for , then will work for .
Aim: whenever we -colour we can find colour-focused arithmetic progressions of length . Let , etc, i.e. for .
Let us look at the indices of these blocks. I colour with colours like so:
We therefore colour with colours. By the definition of , there exists a monochromatic arithmetic progression of length (with respect to ). Say .
So the respective blocks are identically coloured. Look at . It has length , so by induction contains colour-focused arithmetic progressions of length together with their focus.
Let for . Let be their focus. Look at , .
They are monochromatic because the blocks are identically coloured and the s are monochromatic. Since the colour of is the colour of and the s are colour-focused, we must have that the s have pairwise distinct colours.
Remember that the s are are focused at and the colour of is different than the colour of all the s. Note .
Look at . This is an arithmetic progression of length and monochromatic and of a different colour from all of the s.
Enough to show for all , which is equivalent to , which is true as all the s are focused at . □
Non-examinable: what about bounds?
We define the Ackermann hierarchy to be the seqeunce of functions
by
Observe:
These functions grow very fast.
We say that a function is of type if there exists such that
Our bound on was of type .
If you check our proof carefully, then (as a function of ) is bounded by a “type ” bound.
Define: . Then our proof gives a bound that grows faster than any .
Remark. This is often a feature of a double induction proof.
It was believed that does indeed grow this fast.
Shelah (1987) found a proof by just induction on , and showed that .
A prize of $1000 was placed by Graham to show that .
Gowers (1998) showed that , which is “almost type 2”.
The best lower bound is .
Corollary. Whenever is finitely coloured, there exists a colour class that contains arbitrarily long arithmetic progressions.
What about infinite monochromatic arithmetic progressions
No, for example:
Theorem 1.9 (Strengthened Van Waerden). Assuming that:
Proof. By induction on the number of colours. is trivial.
Assume that the case for colours is true. So there exists that works for and .
We will show that works for and . If are -coloured, then there exists a monochromatic arithmetic progression (say red) of length , say .
If any of is red, then we are done: e.g. for some .
If not, the set is -coloured.. This involves a colouring on , therefore there exist and the same colour. This translates to monochromatic. □
Remark. is known as Schur’s Theorem: we can always find monochromatic (for finite colouring of ). In other words, there exists a monochromatic solution to .
Can deduce Schur from Ramsey for pairs: then we induce as follows: . By Ramsey’s Theorem for -sets, there exists such that . Then
Get and monochromatic.
Let be a finite set and is words of length on the alphabet .
Example. and we want combinatorial lines in . If , we get:
If we get:
, then
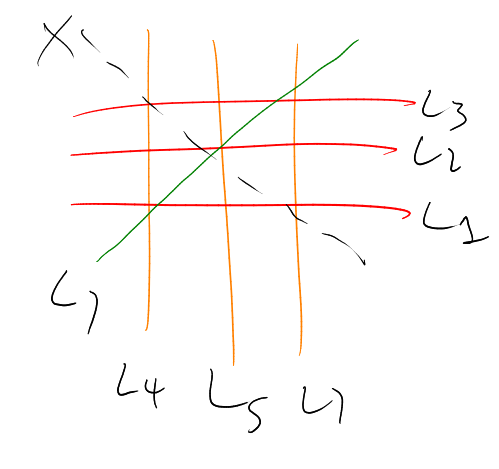
Example. , , or if .
Note. The definition of a combinatorial line is invariant under permutations of .
Theorem 1.11 (The Hales-Jewett Theorem). Assuming that:
Remark.
Proof. Let be a finite colouring of . Let be large enough ()and now colour . is the length of desired arithmetic progression. Define
By The Hales-Jewett Theorem, there exists a monochromatic line
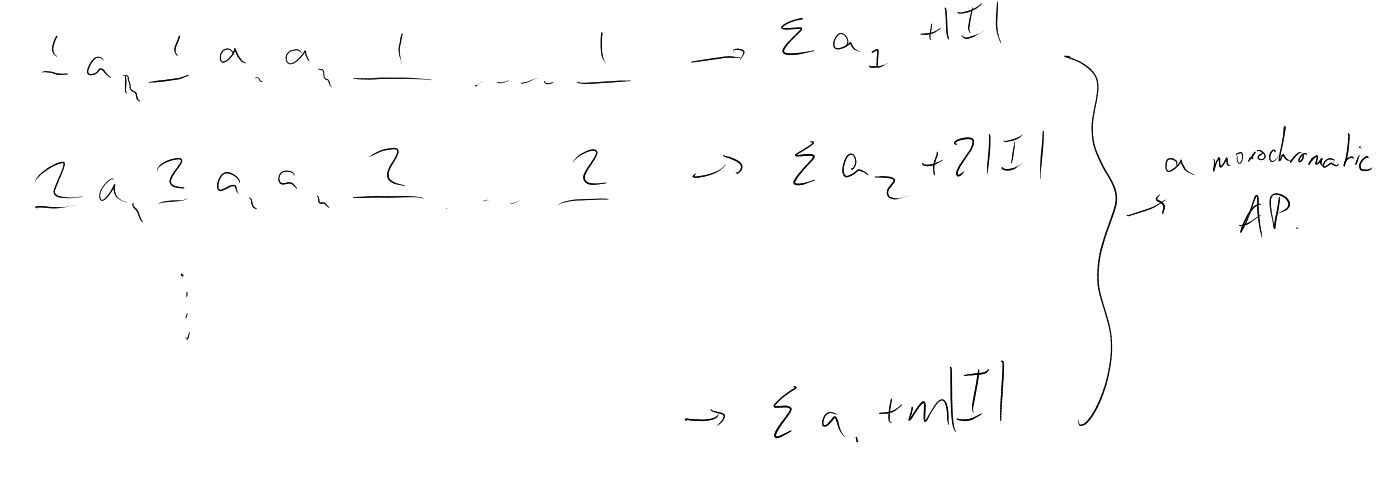
Exercise: Suppose you play Naughts and Crosses with in a line and you play it in high enough dimensions. Show it cannot be a draw (assuming optimal play). Moreover, it is a first player win. Hint: Strategy stealing.
Definition 1.12 (Ordering of chromatic line). If I have a combinatorial line in , then I can order if and only if for all . Let denote the first point in this ordering, and let denote the last point in this ordering.
Definition 1.13 (Focussed (and colour focussed)). Let be combinatorial lines. We call them focussed if for all . For a fixed colouring, they are colour focused if they are focused and monochromatic for each , and they have different colours.
Proof of The Hales-Jewett Theorem. The proof is by induction on the size of the alphabet, i.e. .
is trivially true.
Assume and assume exists for all .
Claim: for every there exists such that in
Then we are done by and looking at the focus.
Now we prove the claim:
: look in We can take .
Now assume and that is suitable for . We will show that is suitable for . Let for convenience.
Need: given a -colouring of with no monochromatic combinatorial lines, we can find colour-focused combinatorial lines. Look at as , with .
Let us colour as follows:
By The Hales-Jewett Theorem there exists a combinatorial lines with active coordinates such that
But now this induces where for any . By the definition of , there exist colour-focused combinatorial lines (for ) , focused at , and with active coordinates .
Finally: look at the combinatorial lines that start at and active coordinates . These give combinatorial lines, and the combinatorial lines that starts at with active coordinates . All focused at . Then done. □
Theorem 1.15 (The Extended Hales-Jewett Theorem). Assuming that:
Proof. In what does a combinatorial line in look like?
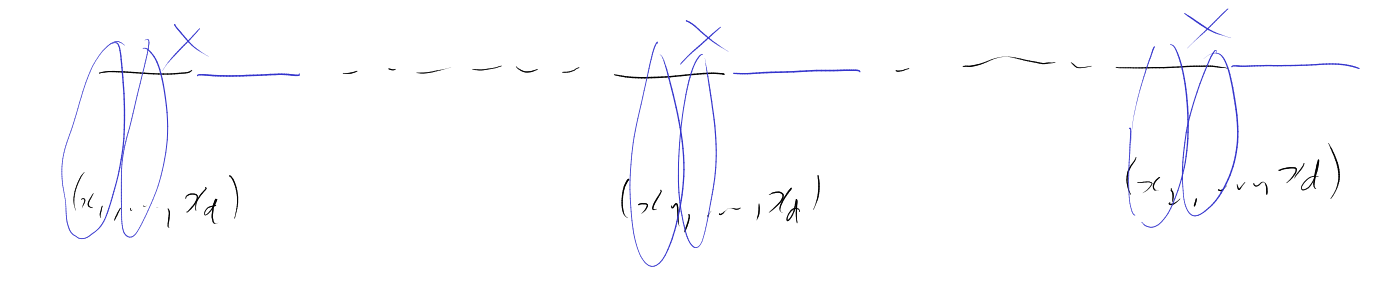
So a monochromatic line in is a monochromatic -point parameter set in .
Letting works. □
Theorem 1.17 (Gallai’s Theorem). Assuming that:
Proof. . Let be a colouring.
We colour (for large enough) as follows:
By The Hales-Jewett Theorem, there exists a monochromatic combinatorial line in with active coordinates . Then
has the same colour for all .
Done as this is a copy of translate by , and dilation factor . □
Remark.
Schur’s theorem: has monochromatic solutions (if is finitely coloured).
Van der Waerden: such that the system
has a monochromatic solution.
Main aim: decide when a system of equations is ‘partition regular’.
Example.
Example.
Aim:
Theorem 2.1 (Rado’s Theorem). A matrix over is partition regular if and only if it has the column property.
Remark.
is partition regular. Take .
Today we will look at a single equation, i.e. a single row matrix.
If we have a matrix, then is partition regular if and only if is also partition regular. So we may assume that .
Observation: has the column property if and only if there exists a set of non-zero elements such that ().
Also note that we may assume that .
We are going to show that if partition regular then it has the column property, which is equivalent to () in this case.
Remark. Even in this case, neither direction of Rado’s Theorem is easy.
Example.
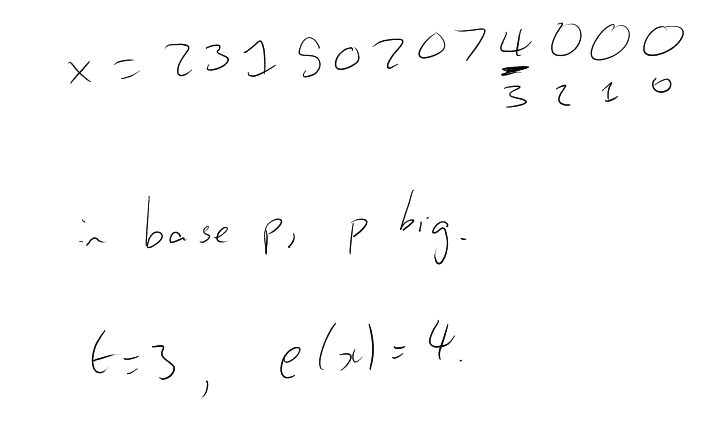
Proposition 2.2. If , is partition regular then it has the column property.
Proof. Let be a huge prime, . I give to the number the colour . Then by assumption, there exists of the same colour such that .
In symbols, let , . When we sum and we look at the last digit , we get , where is the colour of our s. Then . Then (and note is non-empty). □
Remark. To this day, there are no other known proofs of this proposition.
Currently looking at: single equation, i.e. vectors , .
Showed that if is partition regular then it has the column property (recall that in this one dimensional case, having the column property is the same as there exists such that ).
The other direction:
We want to take a vector with and show that it is partition regular.
For we know that it is partition regular if and only if .
For length , is the only non-trivial case with column property. Note is Schur’s theorem.
Remark. We in fact show that whenever is -coloured (), then we have a monochromatic solution.
Proof. If then nothing to show.
If then , so these are equivalent.
Assume , , .
Seek solution to . Let be a finite colouring. Prove this by induction on .
trivial.
Assume this is true for and we want to show it for . Assume is suitable for . We show that is suitable for .
We now have -coloured. There exists a monochromatic arithmetic progression of length , say of colour red. Let us look at , where . Note , so “it is in our set of coloured numbers”.
If is also red, then is a monochromatic solution.
If no such exists, then is coloured. So there exists such that and . Then , i.e. is a monochromatic solution. □
Remark.
Proof. We saw in Proposition 2.2 that if it is partition regular then it has the column property.
For the other direction, we know that and we need to show that given such that there exists monochromatic such that .
Fix and we “cook up” the following vector:
Need monochromatic such that , which is the same as requiring .
Upon dividing by , we see that this is the same as
which is true by Lemma 2.3. □
Remark. Rado’s Boundedness Conjecture: Let be an matrix that is not partition regular. In other words, there exists a bad -colouring for some . Is this bounded, i.e. ?
This is known for matrices (Fox, Kleitman, 2006). colours suffices in this case.
Onto the general case for Rado’s Theorem.
Recall that for a prime and , .
Also recall .
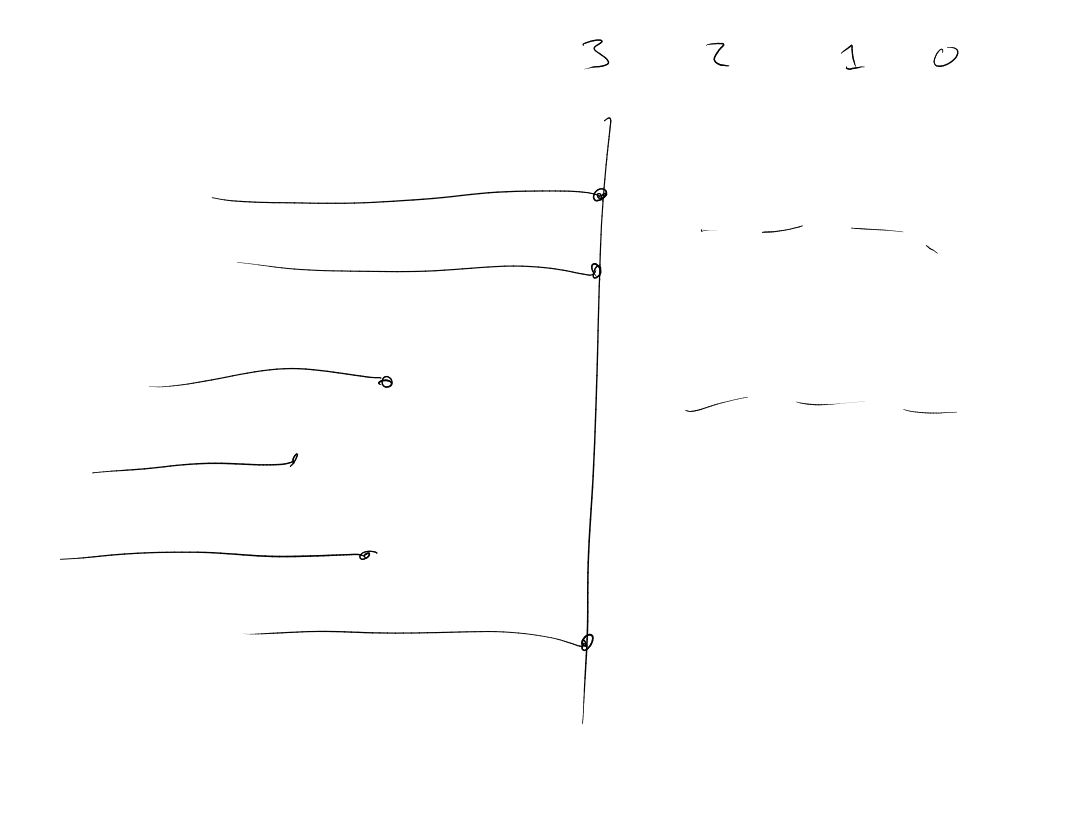
Proof. Let be its columns. Fix prime.
Colour as we did before, by . By assumption there exists monochromatic such that .
Let us partition as where if and only if , , for if and only if .
We do this for infinitely many . Because there exist finitely many partitions, for infinitely many primes we will have the same blocks.
For : , say all have colour , i.e. . Then (by collecting the right-most terms in base ). Since this holds for infinitely many , we have that for infinitely many primes (the large primes), and hence we have that .
.
Then ().
Claim: .
We will show that given such that got sll . Then
which finishes the proof as this implies . Take the inner product of () with . Get
which is equivalent to . Since this happens for infinitely many , we get . □
A crucial notion that puts things into perspective is:
Remark. An -set is sort of a progression of progressions.
Example.
Proof. By the above remark, it is enough to find a -set set such that each row is monochromatic.
Let be large enough (enough in order to apply everything to follow). Let . By Van der Waerden, there exists a monochromatic arithmetic progression of length , with is large enough.
has colour . Let . Now we restrict attention to
Observe that where , is in for any and any . Thus has colour .
Next: look inside :
Apply Van der Waerden to find an arithmetic progression of length , of colour . Let
of colour , and let
Note that for any and . Then
is in , thus has colour .
Keep on doing this times. Restrict to generators (by setting some to ). □
Remark. For the sake of exams (and also in general):
Being “super” pedantic about and bounds is not that important.
The idea is important.
Also known as Folkman’s Theorem
Proof. The previous theorem implies this: any -set contains a set of the above desired form. □
Also: what about products? If then induce by .
By the above for you get such that is constant.
Question: Can we always fine (when finitely coloured) such that the set
is monochromatic?
This is very open …even , i.e. .
Remark.
Proposition 2.8. Assuming that:
Proof. Let be the columns of . Then there exists a partition of such that
For all , we have
with .
For each , let
Rewriting the above we get
for all . We will take . Let be some integers. Let .
Claim is a solution, i.e. . Indeed:
Look at . Have . Let be the common denominator of all the s. Then
Also have that is a solution. Our (for the -set) is indeed the common denominator of the , and . □
Proof of Rado’s Theorem. Want to prove is partition regular if and only if it has the column property.
If is partition regular, then by Proposition 2.5, it has the column property.
For the other direction, let be a finite colouring of . Also, since has column property there exists such that solutions in any -set. By Theorem 2.6 there exists a monochromatic -set with respect to . But this gives a monochromatic solution to . □
Remark. From the proof, we get that if is partition regular for the “” (right-most position in base ) colourings then in fact is partition regular for any colouring. There is no direct proof of this (i.e. that does not go via the Rado’s Theorem proof).
Theorem 2.9 (Consistency Theorem). Assuming that:
Proof. Trivial check of column property. □
This says that if you can solve monochromatically and you can solve monochromatically, then there exists of the same colour such that , .
Remark. You can show this by hand (but much harder).
Proof. . Assume for all that there exists that is partition regular, but has no solution in . Look at
This is partition regular too, hence it has a monochromatic solution of colour say . Then has a solution in , contradiction. □
Rado’s conjecture (1933)
Definition (PR subset). is partition regular if it contains solutions to all partition regular equations.
Rado conjectured that if , then one is also partition regular.
Proved in 1973 by Deuber – introduced -sets. Showed that is partition regular if and only if it contains an -set for all .
He then showed that given , there exists such that whenever an -set is -coloured, there exists a monochromatic -set (this indeed solved the conjecture).
Aim:
This is the first infinite partition regular system in the course.
Definition (Ultrafilter). An ultrafilter is a maximal filter.
Example.
Proposition 2.12. is an ultrafilter if and only if for all , either or is in .
Proof.
By maximality, if is not in then there exists such that . Indeed, suppose not. Then
extends it (the only way this can fail to be a filter is if , which would require a such that ).
Then , so , contradicting the initial assumption. □
Remark. If is an ultrafilter and , . Then either or is in . Indeed, suppost not. Then , hence , i.e. is in . Hence , a contradiction.
Proof. By Zorn’s lemma, it is enough to show that any chain of filters extending has an upper bound.
Let be a chain of filters containing , i.e. for all either or . Let . Need to show is a filter:
and also clearly extends . So is an upper bound. □
Remark.
Definition (). The set of ultrafilters on is called . We define a topology on as the one induced by the following base of open sets
We can see that and because if and only if .
Open sets are .
Closed sets are (using the fact that ).
Remark.
Each point in is isolated because . Under this, is dense in : for an open set and we have .
Proof. is Hausdorff: Let be two ultrafilters. Then there exists such that . Then (and is open), and , hence (and is open). Note . So indeed is Hausdorff.
is compact: want to show that every open cover has a finite subcover. This is equivalent to showing that if a collection of closed sets has the property that no finite subset covers , then the whole collection doesn’t cover . This is equivalent to showing that if you have a collection of closed sets such that they have the finite intersection property (for any finite, ), then their intersection is non-empty.
Further, in the first sentence we can without loss of generality that the open sets are basis sets (i.e. of the form ), and carrying this forward tells us that we may assume that the closed sets in the last sentence are of the form , or equivalently, of the form .
We are given some closed, non-empty sets in . Without loss of generality, they are all for some . Suppose with the finite intersection property. First note , hence .
So let . is a filter because:
Let be an ultrafilter extending . Note: if and only if . Hence . Thus is compact. □
Remark.
Proposition 2.15. Assuming that:
Proof. Let , .
Warning. is not necessarily the same as (there is even a counterexample in the case !).
Example. Let be a non-principal ultrafilter. Let . Then:
is true (since is always true)
is false (since is always false)
Moral. Don’t swap quantifiers!!
Cool fact: we can “add” ultrafilters.
Definition (Addition of ultrafilters). Let be ultrafilters. Then we define
Example. .
Proof that is a filter:
hence by Proposition 2.15(i) applied twice, we have .
Hence is a filter.
Now check that it is an ultrafilter:
Suppose , i.e. is false. By Proposition 2.15(iii) applied twice, this is equivalent to . Hence .
So is indeed an ultrafilter.
Remark. The addition of ultrafilters is associative, i.e.
To show this, we claim if and only if
By similar reasoning, one can also show if and only if the above holds, hence if and only if , which establishes the desired equality.
Let . So . Let . TODO
Last piece of the puzzle: is left continuous: we show that is continuous (for any fixed ).
Proof.
which is equivalent to , so the pre-image is open.
Recall: is compact Hausdorff, with a dense subset, is left continuous, associative, and is non-empty.
Goal: want such that , i.e. idempotent.
Proof. (Warning: we will use Zorn’s lemma :O)
Start with such that . Seek , non-empty, compact and minimal with the property that (hope to show is a singleton).
Proof of existence: there exists such a set, namely itself. Look at all such – this set is not empty. By Zorn’s lemma, it is enough to show that if is a collection of such sets that is also a chain, then has this property also (, is compact).
Compact: We are in a compact Hausdorff space, so a subspace is compact if and only if it is closed. Since the are closed we have that is closed, hence is compact.
Why ? Let , for all . Then for all , hence for all , hence . So .
Also is non-empty: have the finite intersection property (as they are a chain). Since they are closed, we get that the intersection is non-empty.
Therefore, by Zorn’s lemma, there exists a minimal , which is non-empty, compact such that .
Pick . Look at and we want to show that this is .
Claim: .
Proof: . Check:
non-empty
compact, as continuous image () of a compact set
So by minimality .
In particular, there exists such that . Consider .
Claim: . Since , it’s enough to show (by minimality) that is compact, non-empty and . Indeed:
non-empty:
compact as is the pre-image of a singleton (which is compact hence closed), thus closed, thus compact.
for : , , so hence . So .
By minimality, .
So , hence . □
Remark. .
Remark.
Proof of Hindman’s Theorem.
Let be the colour classes () and an idempotent ultrafilter.
Claim: for some (this is because ultrafilters are prime: whenever we have a finite union lying in the ultrafilter we have at least one of the components lying in the ultrafilter, else have for each , hence , but this is , contradicting the fact that ).
Let . Therefore we have . Then:
Then (1) and (2) and (3) give:
Now fix such that
Assume we have found such that
Then have .
Then (1), (2) and (3) give:
Thus fix . Have . Then done by induction.
Remark.
is partition regular (special case of Milliken-Taylor theorem). It was shown in 1995 that and are incompatible.
Launched in 1970 by Erdős, Graham, Montgomery, Rothchild, Spencer and Straus.
Here we want actual copies of some objects.
Colourings of .
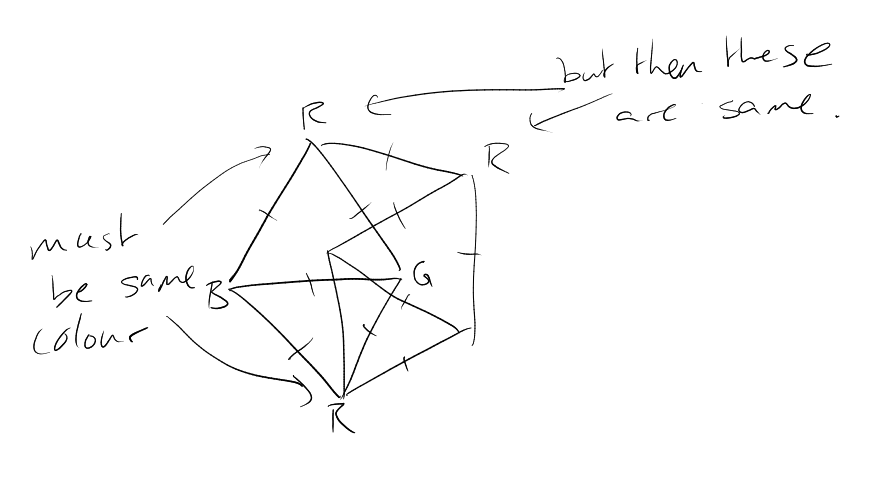
Let us -colour . Then have 2 points of distance of same colour (consider equilateral triangle of side length ).
If we -colour , we can also get 2 points of distance , by considering a regular tetrahedron of side length .
In general, if we -colour , then by looking at the unit regular simplex , then any have distance between them, so we get 2 points having the same colour and being unit distance apart.
Definition (Isometric copy). We say is an isometric copy of if there exists bijection such that .
Definition. We say that a set (finite) is Ramsey (Euclidean Ramsey) if for all there exists a finite set ( could be very big) such that whenever is -coloured, there exists a monochromatic copy of .
Remark.
What about ? Can we do it in ? Yes we can:
This shows (max where is a graph on iwth if and only if ).
Up until 1990, (by using hexagonal colouring idea).
De Grey – 2018: showed using a graph on vertices. Uses nice ideas and computer assistance.
In general, . Lower bound is hard – by Frankl-Wilson. Upper bound is by a type of hexagonal colouring, by Posy.
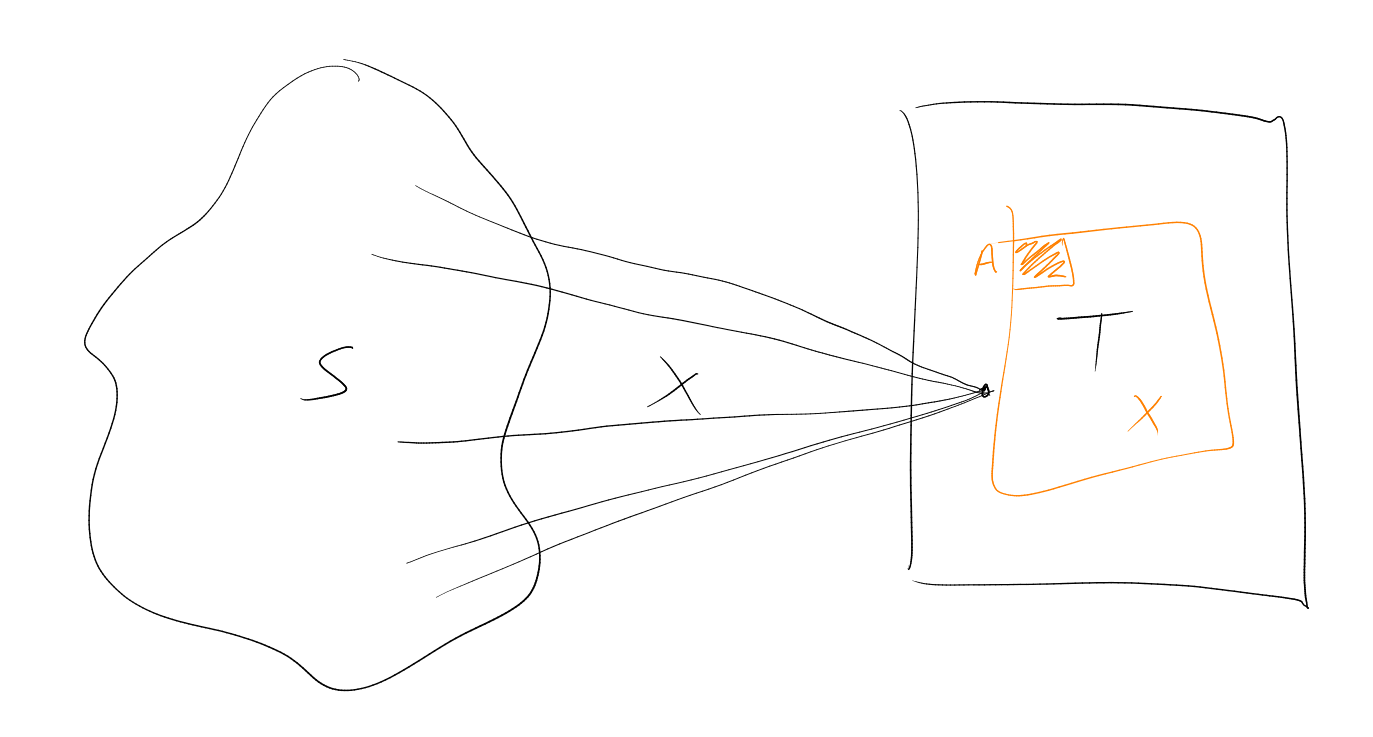
Proposition 3.1. is Euclidean Ramsey if and only if for all , there exists such that whenever is -coloured, there exists a monochromatic copy of .
Proof.
This is a closed set. Let . It has the finite intersection property, because any finite has a bad -colouring. Hence the intersection of all is non-empty. Hence there exists a colouring of with no monochromatic , contradiction. □
How can we generate Ramsey sets?
Proof. Let be a colouring of , where is -Ramsey for and is -Ramsey for .
We -colour as follows:
By choice of , there exists a monochromatic (copy of ) with respect to , i.e. for all and any .
Now -colour via for some (which is well-defined by the above). By the choice of , there exists monochromatic with respect to , and hence is monochromatic with respect to . □
Homework: Convince yourself that this is a very standard product argument.
Next time: non-Ramsey. (think about ?)
Proposition 3.3. is not Ramsey.
Proof. Recall in we have
Every copy of is with (in any ). We have
If we can find a colouring of such that there does not exist a monochromatic solution to . Then use .
We -colour by .
Suppose all have colour . Then implies
where is a multiple of . This is impossible as . □
Remark.
For example, a triangle, a rectangle, any simplex (non-degenerate).
Aim: If is Ramsey, then is spherical.
To do so, we will use a “generalised parallelogram law”.
Lemma 3.4. in are not spherical if and only if there exists , not all , such that:
In the previous proof, we took and being the value in (3).
Proof.
First we note that (1)–(3) are invariant under translation by :
since
Let us look at a minimal subset of that is not spherical. If we can show this for without loss of generality () then take for all .
Since are not spherical, it is not a simplex. Hence there exists such that . Then
Without loss of generality (because the conditions are invariant under reordering the ’s).
Consider . This is spherical by minimality. Suppose the sphere radius is , and centred at . By the above, translate the set such that is centred at . This is fine because the same ’s work after translations ((1)–(3) are totally invariant under translations). Then
as .
Translate the set so that they are centred at the origin (this preserves all conditions and does not vhange the value of ).
Let . Then
so are not spherical. □
Very important: This is tru for every copy of (with the same and !).
Choosing the as in Lemma 3.4. If is a copy of
then as we have seen we can translate and the and are unaffected, and .
After that apply that corresponds to rotation / reflection, and , so (3) holds.
Proof. Suppose is not spherical. Then there exists (not all ) such that and .
Also true for any copy of .
Going to split into for small . Then colour depending on where lies.
Let’s prove that there is a colouring of such that does not have a monochromatic solution. Let . By rescaling, we may assume . Now we split into intervals where is very small. Let
A -colouring.
Assume monochromatic under and such that .
Hence the sum is within of an integer, so not , if small enough. □
We have showed Ramsey implies spherical.
What about spherical implies Ramsey?
Still an open question (1975).
What is known:
Aim: To show tht a regular -gon is Ramsey.
Roughly speaking:

Definition (-invariant). For a finite , we say that a colouring of is -invariant if it is invariant under chaning the coordinates within . i.e. for , if either or implies .
“boosting from -constant to -invariant.”
Proof. (Yawn, product argument…)
We will by induction on (and all at once).
is just the assumption.
Suppose true for . Fix . Let be a finite set such that whenever is coloured, there exists an -invariant copy of .
a finite set such that whenever is -coloured, there exists a copy of with monochromatic.
Claim: works for .
By definition of , if we look at , a -colouring. Thus there exists a copy of with monochromatic.
This induces a colouring of as follows: for some (note is well-defined). This is a -colouring.
Therefore by the choice of , there exists a copy of that is -invariant.
Then we are done as this copy of in is -invariant. □
Next time:
Theorem 3.8 (Kriz Theorem). Every regular -gon is Ramsey.
Note. We will show that we can find monochromatic, which is a copy of , but scaled by (which is fine as is constant).
Proof. , where the numbers are the names of points.
We find a copy of of the form
We will show by induction on and all at once that we can find a copy of with monochromatic.
is trivial as it is just a point.
is 2 points at a specified distance (which we showed is Ramsey).
Assume true for and all . By Our product argument, there exists and such that we have a (copy) on which the colouring is -invariant on (for any ). We will choose to be as big as we want.
The clever bit:

We will colour sets in say as follows.

is a colouring of .
As can be taken as big as needed, by Ramsey there exists a -monochromatic set. By relabeling, we may assume that this set is coordinates.

Now we look at the following:

with this we note that the colour of is the same as the colour of .
Now look at: , , …, . monochromatic copy of . They all have the same colour (ignoring this). □
Remark. Same proof works for any cyclic set: i.e. a set such that the map (modulo ) is a symmetry of the set.
Or equivalently, there exists a cyclic transitive symmetry group on .
The following discussion is non-examinable (until told otherwise).
A soluble group is “built” up from cyclic groups.
Theorem (Kriz). If hs a soluble, transitive symmetry group, then is Ramsey.
Rival conjecture to the spherical conjecture (2010, Leader, Russell, Walters):
is Ramsey if and only if is subtransitive (subtransitive means that it can be embedded in a transitive set, i.e. it can be embedded in a set that has a transitive isometry group).
Why are they rival?
spherical does not imply sub-transitive.
sub-transitive does imply spherical: let be sub-transitive. Embed into transitive. There exists a unique minimal sphere containing , which is preserved by the isometry group.
For spherical doesn’t imply sub-transitive: the kite.

This is not sub-transitive.
What happens if the kite is Ramsey? It would disprove the 2010 conjecture. If not Ramsey, it would disprove the original conjecture.
It is believed that the transitive conjecture is true.
It could also be the case that neither is true :?.
End of non-examinable discussion.
˙