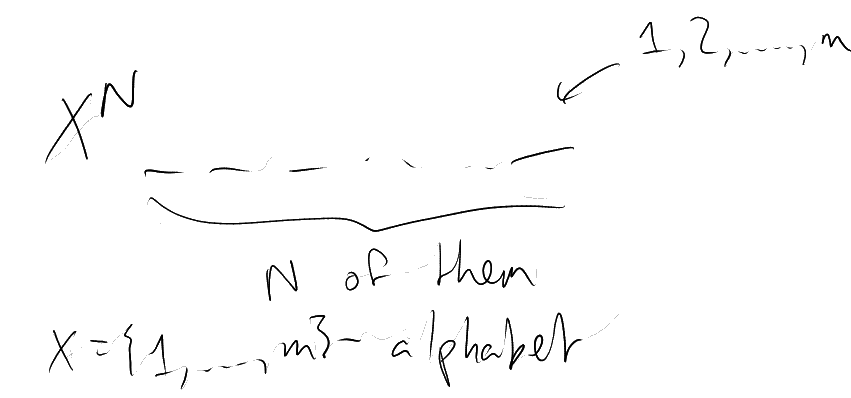3 Euclidean Ramsey
Launched in 1970 by Erdős, Graham, Montgomery, Rothchild, Spencer and Straus.
Here we want actual copies of some objects.
Colourings of .
Let us -colour
. Then have 2 points of distance
of same colour (consider
equilateral triangle of side length ).
If we -colour
, we can also get 2 points of
distance , by considering a regular
tetrahedron of side length .
In general, if we -colour
, then by looking at the
unit regular simplex ,
then any have
distance
between them, so we get 2 points having the same colour and being unit distance apart.
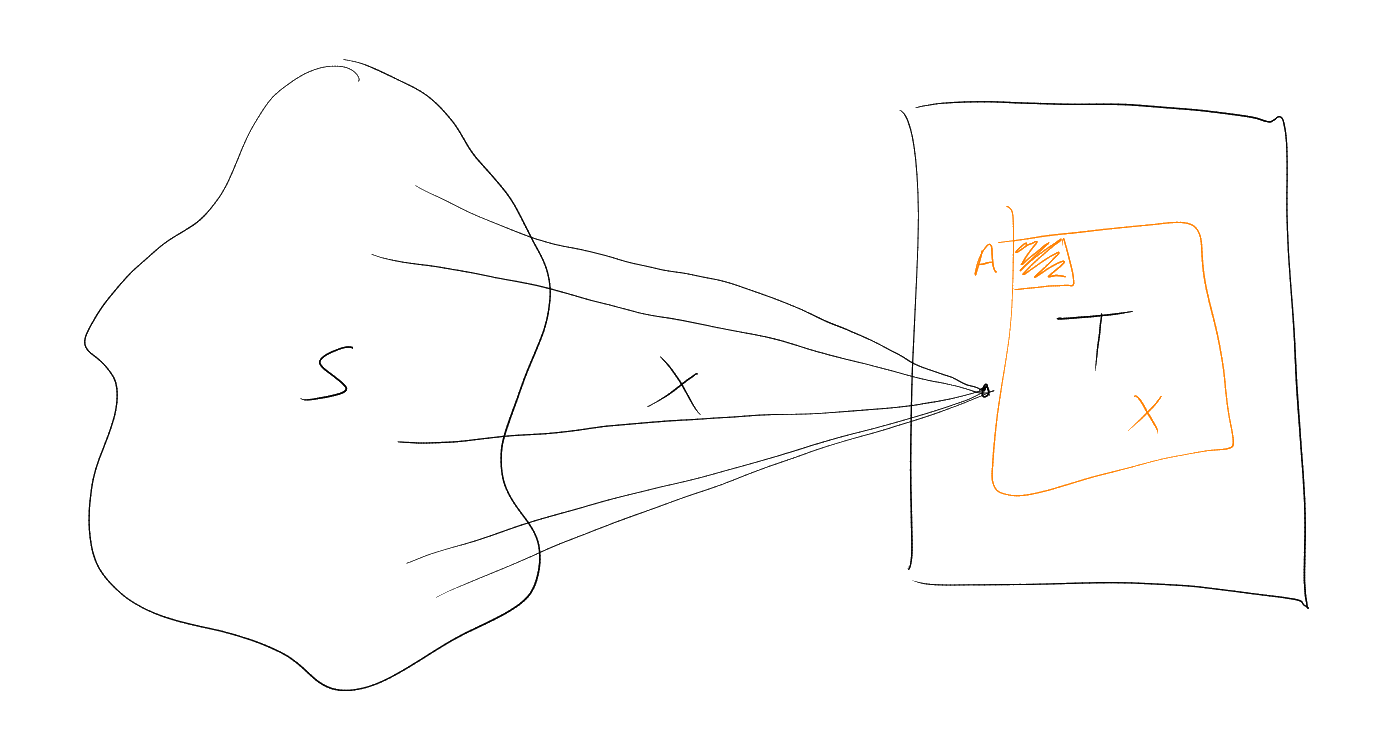
Definition (Isometric copy).
We say
is an isometric copy of
if there exists
bijection such that .
Definition.
We say that a set
(finite) is Ramsey (Euclidean Ramsey) if for all
there exists a finite set
(
could be very big) such that whenever
is -coloured,
there exists a monochromatic copy of .
Example.
-
(1)
is Ramsey: for -colours,
take a -dimensional
unit simplex.
-
(2)
Unit equilateral triangle is Ramsey: for -colours,
can take -dimensional
unit simplex.
-
(3)
Similarly have that any
is Ramsey.
-
(4)
Similarly any regular simplex is Ramsey.
Remark.
-
(1)
If
is infinite, then can build a -colouring
of
with no monochromatic
(exercise).
-
(2)
We took for -colours
to be in .
Can we do better? For ,
can we do it in ?
Colour .
Need
dimensions or higher.
What about ?
Can we do it in ?
Yes we can:
This shows
(max where
is a graph
on iwth
if and
only if ).
Up until 1990,
(by using hexagonal colouring idea).
De Grey – 2018: showed
using a graph on
vertices. Uses nice ideas and computer assistance.
In general, .
Lower bound is hard – by Frankl-Wilson. Upper bound is by a type of hexagonal colouring, by
Posy.
Proposition 3.1.
is Euclidean
Ramsey if and only if for all ,
there exists such
that whenever is
-coloured, there exists a
monochromatic copy of .
Proof.
-
If
is Euclidean Ramsey then take
finite in
(for -colours).
-
We know that for all -colourings
of , there exists a
monochromatic copy of
(by compactness). Suppose not. Therefore, for any set
finite in
, there exists a bad colouring (i.e.
not a copy of monochromatic).
Space of all -colourings
is ,
which is compact by Tychonoff. Let
|
|
This is a closed set. Let .
It has the finite intersection property, because any finite
has a bad -colouring.
Hence the intersection of all
is non-empty. Hence there exists a colouring of
with no monochromatic ,
contradiction. □
How can we generate Ramsey sets?
Lemma 3.2.
Assuming that:
Remark.
-
is Ramsey, and so is .
So
rectangles are Ramsey. In particular, any right angled triangle is Ramsey.
By considering ,
we can acute angled triangles:
Proof.
Let
be a colouring of ,
where
is -Ramsey
for
and
is -Ramsey
for .
We -colour
as
follows:
|
|
By choice of ,
there exists a monochromatic
(copy of )
with respect to ,
i.e.
for all
and any .
Now -colour
via
for some
(which is well-defined by the above). By the choice of ,
there exists monochromatic
with respect to ,
and hence
is monochromatic with respect to .
□
Homework: Convince yourself that this is a very standard product argument.
Remark.
-
(1)
In general to prove sets are Ramsey we will first embed them into other sets (with ‘cool’ symmetry
groups) and show that those sets are Ramsey.
-
(2)
Spoiler:
Next time: non-Ramsey. (think about ?)
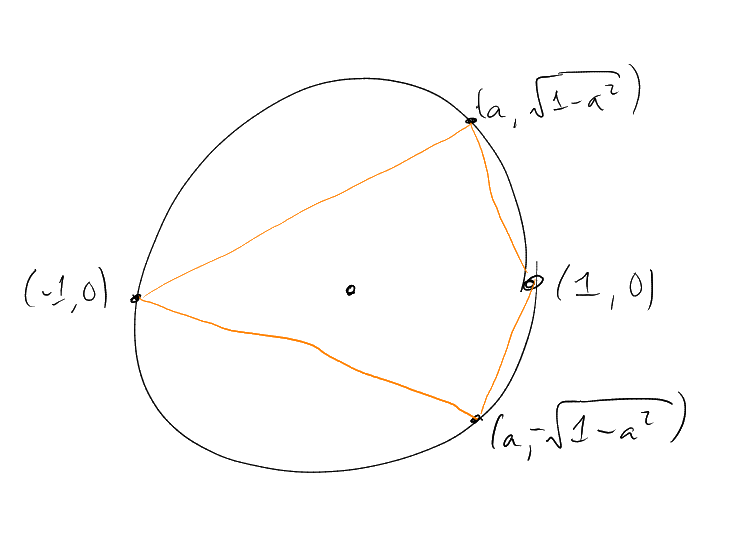
Proposition 3.3.
is not Ramsey.
Proof.
Recall in
we have
|
|
Every copy of
is with
(in any
). We
have
|
|
If we can find a colouring of
such that there does not exist a monochromatic solution to .
Then use .
We -colour
by .
Suppose all
have colour .
Then
implies
where
is a multiple of .
This is impossible as .
□
Remark.
-
(1)
For all ,
there is a -colouring
of
that stops every copy of
from being monochromatic.
-
(2)
Very important in ,
we got this
to not be .
-
(3)
It will turn out that the property that made
not Ramsey is “it does not lie on a sphere”.
Definition (Spherical).
A set
is called spherical if it lies on the surfcace of a sphere.
For example, a triangle, a rectangle, any simplex (non-degenerate).
Definition (Simplex).
Let
be some points. They form a simplex if
are linearly independent. In other words, they do not lie in a -dimensional
affine space.
Aim: If is
Ramsey, then
is spherical.
To do so, we will use a “generalised parallelogram law”.
Lemma 3.4.
in
are not spherical if
and only if there exists ,
not all ,
such that:
-
(1)
-
(2)
-
(3)
In the previous proof, we took
and
being the value in (3).
Proof.
-
are not spherical. The first two conditions say that
is not a simplex: so there exists
(not all )
such that
or .
First we note that (1)–(3) are invariant under translation by
:
-
since
-
Let us look at a minimal subset of
that is not spherical. If we can show this for without loss of generality
() then
take for
all .
Since are not spherical, it is not
a simplex. Hence there exists
such that .
Then
|
|
Without loss of generality
(because the conditions are invariant under reordering the
’s).
Consider .
This is spherical by minimality. Suppose the sphere radius is
, and centred at
. By the above, translate
the set such that is
centred at . This is fine
because the same ’s
work after translations ((1)–(3) are totally invariant under translations). Then
|
|
as .
-
Suppose there exists as in
the statement, and assume
are spherical, centred at ,
radius .
Translate the set so that they are centred at the origin (this preserves all conditions and does not vhange the
value of ).
Let .
Then
so
are not spherical. □
Corollary 3.5 (Generalised parallelogram law).
Assuming that:
Then there exists
not all with
and there
exists such
that .
Very important: This is tru for every copy
of (with the
same
and !).
Choosing the as
in Lemma 3.4. If
is a copy of
then as we have seen we can translate and the
and are
unaffected, and .
After that apply that corresponds
to rotation / reflection, and ,
so (3) holds.
Theorem 3.6.
Assuming that:
Proof.
Suppose
is not spherical. Then there exists
(not all )
such that
and .
Also true for any copy of .
Going to split
into
for small .
Then colour depending on where
lies.
Let’s prove that there is a colouring of
such that does not have a
monochromatic solution. Let .
By rescaling, we may assume .
Now we split
into intervals
where
is very small. Let
|
|
A -colouring.
Assume
monochromatic under
and such that .
Hence the sum is within
of an integer, so not ,
if
small enough. □
We have showed Ramsey implies spherical.
What about spherical implies Ramsey?
Still an open question (1975).
What is known:
-
(1)
Triangles are Ramsey, simplices are Ramsey, (old stuff). In 1991, Kriz showed that a regular
pentagon is Ramsey and that any regular -gon
is Ramsey. His proof is unbelievably clever!
Aim: To show tht
a regular -gon
is Ramsey.
Roughly speaking:
-
(1)
First find a copy of
such that
and
are monochromatic.
-
(2)
Use a product argument to get a copy of
(with very large), such that the
colouring is invariant under .
e.g.
-
(3)
The above plus some clever stuff to find a copy of
on
which
is monochromatic.
Definition (-invariant).
For a finite ,
we say that a colouring of
is -invariant
if it is invariant under chaning the coordinates within .
i.e. for ,
if
either
or
implies .
Proposition 3.7 (Our product argument).
Assuming that:
Then for all , there
exists finite such
that whenever
is -coloured there
exists a copy of
that is -invariant.
“boosting from -constant
to -invariant.”
Proof.
(Yawn, product argument…)
We will by induction on
(and all
at once).
is just the assumption.
Suppose true for .
Fix . Let
be a finite set such
that whenever
is coloured, there
exists an -invariant
copy of .
a finite set such
that whenever
is -coloured, there
exists a copy of
with
monochromatic.
Claim:
works for .
By definition of ,
if we look at , a
-colouring. Thus
there exists a copy of
with
monochromatic.
This induces a colouring of
as follows: for
some (note
is well-defined).
This is a -colouring.
Therefore by the choice of ,
there exists a copy of
that is -invariant.
Then we are done as this copy of
in is
-invariant.
□
Next time:
Theorem 3.8 (Kriz Theorem).
Every regular
-gon is
Ramsey.
Note.
We will show that we can find
monochromatic, which is a copy of ,
but scaled by
(which is fine as
is constant).
Proof.
,
where the numbers are the names of points.
We find a copy of
of the form
|
|
We will show by induction on
and all at once that
we can find a copy of
with
monochromatic.
is
trivial as it is just a point.
is 2
points at a specified distance (which we showed is Ramsey).
Assume true for and
all . By Our product
argument, there exists
and such that we have
a (copy) on which the
colouring is -invariant
on (for any
). We will
choose
to be as big as we want.
The clever bit:
We will colour
sets in
say as
follows.
is a
colouring of
.
As
can be taken as big as needed, by Ramsey there exists a
-monochromatic set. By relabeling,
we may assume that this set is
coordinates.
Now we look at the following:
with this we note that the colour of
is the same as the colour of .
Now look at: ,
, …,
. monochromatic
copy of .
They all have the same colour (ignoring this). □
Remark.
Same proof works for any cyclic set: i.e. a set
such that the map
(modulo )
is a symmetry of the set.
Or equivalently, there exists a cyclic transitive symmetry group on
.
Example.
Given by rotation
and reflection. Generates order .
This is Ramsey.
The following discussion is non-examinable (until told otherwise).
A soluble group is “built” up from cyclic groups.
Theorem (Kriz).
If hs a soluble,
transitive symmetry group, then
is Ramsey.
Rival conjecture to the spherical conjecture (2010, Leader, Russell, Walters):
is Ramsey if
and only if
is subtransitive (subtransitive means that it can be embedded in a transitive set, i.e. it can be embedded in a
set that has a transitive isometry group).
Why are they rival?
spherical does not imply sub-transitive.
sub-transitive does imply spherical: let
be sub-transitive. Embed into
transitive. There exists a unique minimal sphere containing
, which
is preserved by the isometry group.
For spherical doesn’t imply sub-transitive: the kite.
This is not sub-transitive.
What happens if the kite is Ramsey? It would disprove the 2010 conjecture. If not Ramsey, it would disprove
the original conjecture.
It is believed that the transitive conjecture is true.
It could also be the case that neither is true :?.
End of non-examinable discussion.