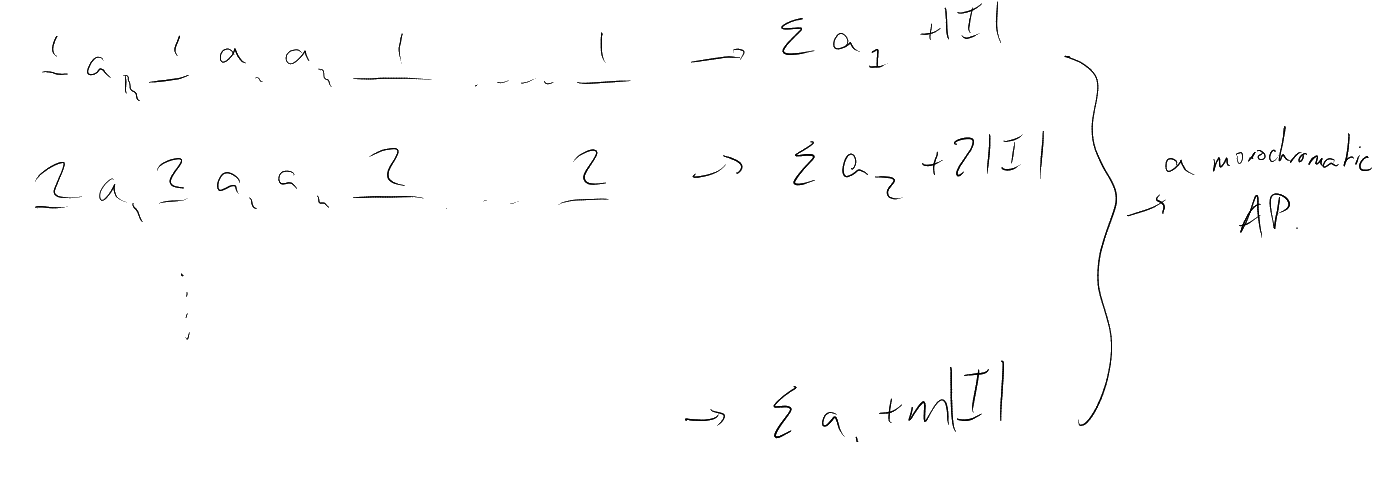1 Ramsey’s Theorem
Notation.
,
for a
set ,
,
.
Given a 2-colouring of ,
are we guaranteed to have an infinite monochromatic set (i.e.
,
infinite such that the
colouring is constant on )?
Example.
-
(1)
red if
even, odd otherwise. Then
works.
-
(2)
red if
is even, blue otherwise. Then
works.
-
(3)
red if
has an even number of distinct prime divisors, and blue otherwise. No explicit
is known!
Theorem 1.1 (Ramsey’s Theorem for pairs).
Assuming that:
Then there exists
infinite monochromatic.
Proof.
Pick .
Then there exists an infinite set
such that
for all .
Pick
and find
(infinite) such that
for all .
Keep on doing this. We end up with
and
such that
for all .
One colour appears infinitely many times .
Now note
is a monochromatic set. □

Remark.
-
(1)
The same proof works for
colours. This is referred to as a “-pass”
proof. Alternatively: if we have colours ,
then we can consider
to be red, and everything else to be blue. Then using the above result and induction, we get an
alternative way to prove the theorem for greater than
colours.
-
(2)
Infinite monochromatic is very different than arbitrarily large monochromatic.
For example: suppose we write ,
,
and so on. Say
is red if there exists
such that ,
and blue otherwise. Then there exist arbitrarily large monochromatic red sets, but no infinite
monochromatic red set.
What about
with ?
Example.
,
,
red if and
only if .
Then is
monochromatic.
Theorem 1.2 (Ramsey’s Theorem for -sets).
Assuming that:
Then there exists a monochromatic infinite set.
Proof.
pigeonhole,
is Theorem 1.1. Prove this by induction.
Assume it is true for .
Given ,
we must find
(infinite and monochromatic). Pick .
Look at the
sets of .
Define
via .
By induction there exists
such that
is constant on it, say constantly equal to .
Now pick
and induce
defined by .
By induction there exists
such that
is constant on it, say equal to .
Continuing this, we end up with
and sets
such that
with
for all ,
.
Some colour must appear infinitely many times: say .
Check:
is monochromatic. □
Example.
Applications:
-
(1)
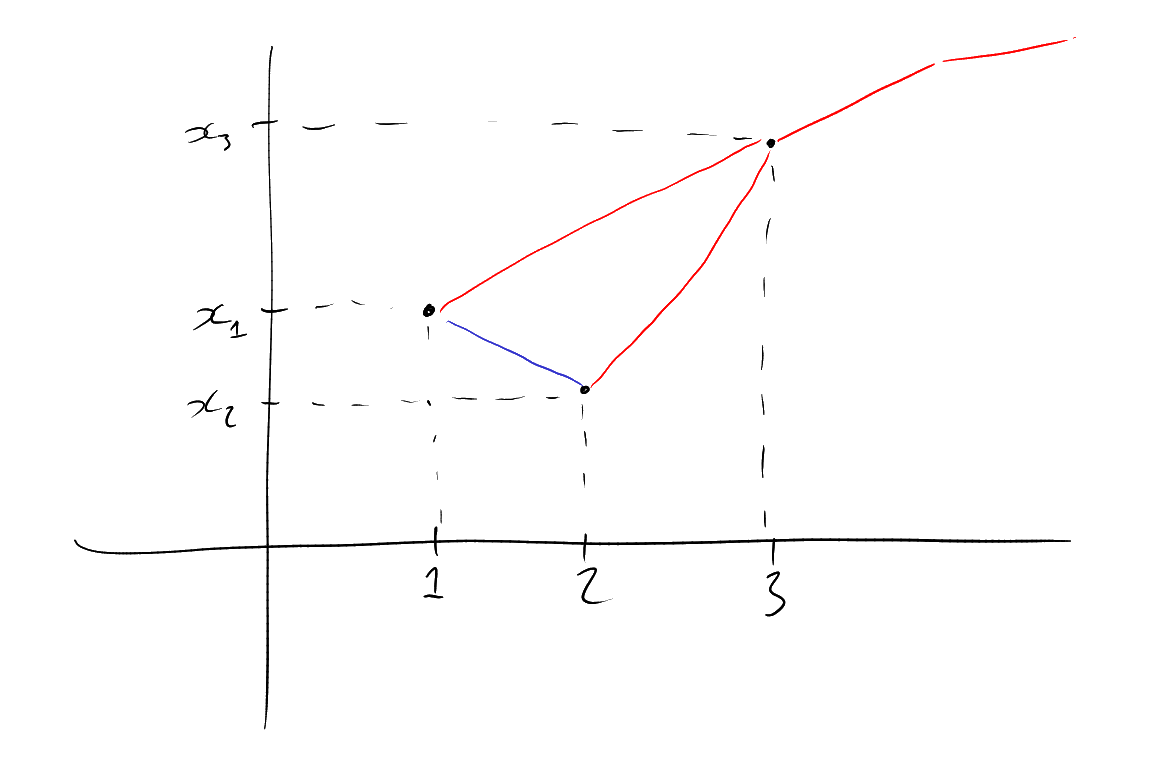
In a totally ordered set, any sequence has a monotone subsequence.
Proof.
Let the sequence be .
Say
is red if ,
and blue otherwise. By Theorem 1.1, we may find
monochromatic. If
is red, then the sequence
is increasing, and if
is blue then the sequence is strictly decreasing. □
-
(2)
Using a slightly adjusted argument, we can insist that the function given by
is either concave or convex.
We do this by: for a triple
we colour it convex or concave. Then apply Theorem 1.2.
From Theorem 1.2 we can deduce:
Theorem 1.3 (Finite Ramsey).
Assuming that:
Then there exists
such that whenever is
-coloured, we can find a
monochromatic set of size .
Proof.
Suppose not. Then for each
we can find with no monochromatic
-sets. Note that there are only
finitely many ways to -colour
. So infinitely
many will
agree on .
Pick such
that for all ,
We can do the same on
and produce some
such that
is constant on .
Continuing this, we get .
They satisfy:
-
(1)
There is no monochromatic -set
for any
(because ).
-
(2)
These ’s
are nested:
for .
Finally: colour
via , where
is any
integer .
One can see that this is well defined, and gives a contradiction to Theorem 1.2. □
Remark.
-
(1)
This proof gives no bound on this .
There are other proofs that give some bounds.
-
(2)
This is a “proof by compactness”: what we (essentially) showed is that
with the product topology is (sequentially) compact. If you prefer, the product topology can be thought
of as the topology derived from the metric
|
|
What happens if we have
with
being potentially infinite?
Theorem 1.4 (Canonical Ramsey Theorem).
Assuming that:
Then there exists an infinite set
such that one of the following holds:
-
(i)
is constant on .
-
(ii)
is injective on .
-
(iii)
if and only if
for ,
in .
-
(iv)
if and only if ,
for all ,
.
Proof.
We colour an element
of
as follows: We say that it is red if ,
and blue otherwise.
By Ramsey’s Theorem for -sets,
there exists an infinite set
that is monochromatic under this colouring.
-
(1)
Suppose
is red. Then
is constant on .
Let ,
.
Pick
(in )
bigger than all .
Then
hence .
Also, ,
so .
So
is constant on .
-
(2)
Now let’s assume
is blue. So for
we have .
Next: colour
as follows: we will say that
is green if ,
and purple otherwise. By Ramsey’s Theorem for -sets
we can pick infinite
monochromatic.
We claim that cannot be
green. This is because if
is green, let
in .
Then:
But using these we get , which
contradicts the fact that
is blue.
Therefore is
purple: for
we have .
Next we colour as
follows: is orange if
, and white otherwise. Again,
by Ramsey’s Theorem for -sets
we can pick an infinite
such that it is monochromatic with respect to this colouring.
We claim that cannot be orange.
If it is, then we again consider :
Hence , which
contradicts the fact that
is blue.
Therefore
is white. This finally tells us (using earlier working) that given any pair disjoint edges, the colours must
be different.
Now, we colour
via: yellow if
, and pink otherwise. By
Ramsey’s Theorem for -sets,
there is an infinite
that is monochromatic.
We claim that is not
yellow. If it is, then given ,
we have ,
which contradicts blueness.
Thus for any
in , we
have .
Finally: we colour
with 4 colours, with
coloured according to:
-
turquoise if
and
-
magenta if
and
-
cyan if
and
-
maroon if
and
By Ramsey’s Theorem for -sets,
there exists a monochromatic set .
It cannot be turquoise because
contradicts .
Then:
Theorem 1.5.
Assuming that:
Then we can find an infinite set
and such
that for any
in , and
in
we have
if and
only if
for all .
Example.
In the previous theorem:
-
(i)
-
(ii)
-
(iii)
-
(iv)
These colourings are call the
“canonical colourings” of .
Proof.
Exercise. Note that this proof is examinable (because the ideas are exactly the same as those
in the previous theorem). □
1.1 Van der Waerden’s Theorem
We will colour .
Aim 1: Whenever we -colour
, we find a monochromatic
arithmetic progression of length
for any .
The abbreviation A.P. can be used to mean “arithmetic progression”, i.e. a sequence of the form
.
Aim 2: For any ,
there exists such
that whenever
are -coloured,
there exists a monochromatic arithmetic progression of length
.
This is equivalent to Aim 1, by using a proof by compactness argument like before:
If Aim 2 is not true, then we can find
such that infinitely many agree on .
Of those infinitely many agree on ,
etc. Keep going (as before), and then get a colouring of
without a monochromatic
arithmetic progression of length .
The other direction is easier.
We will show something a bit stronger (because it turns out to be easier): we will prove Aim 2 but with
colours.
This is in contrast with the earlier theorems, where the proofs were slightly easier to think about with just 2
colours.
Example.
and are
focused at .
Theorem 1.7.
Assuming that:
Then we can find a monochromatic
arithmetic progression of length
(equivalently,
for any
we
find an
that works).
Proof.
Claim: For any
there exists an
such that if
is -coloured
then either:
The proof is by induction on .
Base case we
can take ,
since 2 numbers will have the same colour.
Suppose the result is true for
and let
be an
that satisfies the property in the claim.
We will show that
works for . Let
be a colouring. We will
split the ground set into
blocks of length .
Call the blocks .
If there exists a monochromatic arithmetic progression of length
in this
colouring, then we are done. So assume not.
By the induction hypothesis, the first half of each
has colour-focused arithmetic
progressions of length .
Because ,
each block also contains their focus.
For a set , there are
exactly ways to
-colour it. So there
exists two blocks
and
that are identically coloured.
Let be the
colour-focused arithmetic
progressions in .
Then are the
corresponding ones in .
Let be the
focus in , so
therefore is
the focus in .
Now take
for , and
. Since
, we have
. So all
of these sequences
are focused at .
We know that and
are monochromatic
by the choice of ,
. Why colour focused?
have different colours by induction
hypothesis. Also, because
was assumed to have no monochromatic arithmetic progression of length
, the colours of
must be different to all the
colours of the above arithmetic
progressions of length . Thus
we have colour-focused
arithmetic progressions of length
in .
□
Remark.
The idea of looking at all the possible colouring of a set is referred to as the “product argument”.
The Van der Waerden number
is the smallest such
that whenever
is -coloured,
there exists a monochromatic arithmetic progression of length
.
Proof above claims that msup
for a tower of size .
“tower-type bound”.
Theorem 1.8 (Van der Waerden).
Assuming that:
Then there exists an
such
that whenever we
-colour
we can find a monochromatic
arithmetic progression of length
.
Recall that we defined
to be the smallest (if it
exists) such that whenever
is -coloured,
there exists a monochromatic arithmetic progression of length
.
Proof.
This will be by induction on .
For any :
is trivial.
is pigeonhole.
is Theorem 1.7.
Assume that this is true for some
fixed, but for any .
In other words,
exists for all .
Claim: For every
there exists
such that we always have one of the following:
When
we are done by looking at the focus. Now we prove the claim. We will prove it by induction on
.
For we can
take .
Now assume that the result is true for
and that there does not exist a monochromatic arithmetic progression of length
. We will
show that
works for ,
then will
work for .
Aim: whenever we -colour
we can find
colour-focused arithmetic
progressions of length .
Let ,
etc, i.e.
for
.
Let us look at the indices of these blocks. I colour
with
colours
like so:
|
|
We therefore colour with
colours. By the definition of
, there exists a monochromatic
arithmetic progression of length
(with respect to ).
Say .
So the respective blocks are
identically coloured. Look at .
It has length , so by
induction contains
colour-focused arithmetic
progressions of length
together with their focus.
Let for
. Let
be their focus.
Look at ,
.
They are monochromatic because the blocks are identically coloured and the
s are monochromatic.
Since the colour of is
the colour of and the
s are colour-focused, we
must have that the s
have pairwise distinct colours.
Remember that the s are
are focused at and the
colour of is different
than the colour of all the s.
Note .
Look at . This is an arithmetic
progression of length
and monochromatic and of a different colour from all of the
s.
Enough to show
for all , which is
equivalent to , which
is true as all the s
are focused at .
□
Non-examinable: what about bounds?
We define the Ackermann hierarchy to be the seqeunce of functions
by
Observe:
msupmsup
These functions grow very fast.
We say that a function
is of type if
there exists
such that
Our bound on
was of type .
If you check our proof carefully, then
(as a function of ) is
bounded by a “type ”
bound.
Define: . Then our proof gives a
bound that grows faster than any .
Remark.
This is often a feature of a double induction proof.
It was believed that
does indeed grow this fast.
Shelah (1987) found a proof by just induction on ,
and showed that .
A prize of $1000 was placed by Graham to show that .
Gowers (1998) showed that ,
which is “almost type 2”.
The best lower bound is .
Corollary.
Whenever
is finitely coloured, there exists a colour class that contains arbitrarily long arithmetic progressions.
What about infinite monochromatic arithmetic progressions
No, for example:
-
(1)
colour
red,
blue,
red, etc
-
(2)
Or “just do it”: the set of arithmetic progressions in
is countable. So let them be .
Pick
in ,
and colour
red,
blue. Next go to
and select
in .
Colour
red,
blue. Keep going...
Theorem 1.9 (Strengthened Van Waerden).
Assuming that:
Then there exists
such that whenever
is
-coloured,
there exists a monochromatic
arithmetic progression of length
together with their common
differences, i.e. the set
is monochromatic.
Proof.
By induction on the number of colours.
is trivial.
Assume that the case for
colours is true. So there exists
that works for
and .
We will show that
works for
and .
If
are -coloured,
then there exists a monochromatic arithmetic progression (say red) of length ,
say .
If any of
is red, then we are done: e.g.
for some .
If not, the set
is -coloured..
This involves a
colouring on ,
therefore there exist
and
the same colour. This translates to
monochromatic. □
Remark.
is known as Schur’s Theorem: we can always find
monochromatic (for finite colouring of ).
In other words, there exists a monochromatic solution to .
Can deduce Schur from Ramsey for pairs:
then we induce as
follows: . By Ramsey’s
Theorem for -sets,
there exists
such that .
Then
|
|
Get
and
monochromatic.
1.2 The Hales-Jewett Theorem
Let be a finite
set and is words
of length on
the alphabet .
Definition 1.10 (Combinatorial line).
A combinatorial line in
is a set
of the following form:
|
|
Example.
and we want
combinatorial lines in .
If , we
get:
If we
get:
, then
Example.
,
, or if
.
Theorem 1.11 (The Hales-Jewett Theorem).
Assuming that:
Then there exists
such
that whenever we
-colour
there
exists a monochromatic
combinatorial line.
Exercise: Suppose you play Naughts and Crosses with
in a
line and you play it in high enough dimensions. Show it cannot be a draw (assuming optimal play). Moreover,
it is a first player win. Hint: Strategy stealing.
Definition 1.12 (Ordering of chromatic line).
If I have a combinatorial line
in ,
then I can order
if and only if
for all .
Let
denote the first point in this ordering, and let
denote the last point in this ordering.
Definition 1.13 (Focussed (and colour focussed)).
Let
be combinatorial lines. We call them focussed if
for all .
For a fixed colouring, they are colour focused if they are focused and
monochromatic for each ,
and they have different colours.
Proof of The Hales-Jewett Theorem.
The proof is by induction on the size of the alphabet, i.e. .
is trivially true.
Assume
and assume
exists for all .
Claim: for every
there exists such
that in
Then we are done by
and looking at the focus.
Now we prove the claim:
: look in
We can
take .
Now assume
and that is
suitable for . We
will show that
is suitable for .
Let for
convenience.
Need: given a
-colouring of
with no monochromatic combinatorial
lines, we can find colour-focused
combinatorial lines. Look at
as , with
.
Let us colour
as follows:
|
|
By The Hales-Jewett Theorem there exists a combinatorial lines
with active
coordinates
such that
|
|
But now this induces
where for any
. By the definition
of , there exist
colour-focused
combinatorial lines (for )
, focused at
, and with active
coordinates .
Finally: look at the combinatorial lines that start at
and active coordinates
. These give
combinatorial lines, and the
combinatorial lines that starts at
with active coordinates .
All focused at .
Then done. □
Definition 1.14 (-dimensional space).
A -dimensional
space or a
-point parameter set is a
set such that there exists
disjoint and ,
and if
and only if:
Theorem 1.15 (The Extended Hales-Jewett Theorem).
Assuming that:
Then there exists
such that whenever
is
-coloured, there
exists a
-point
parameter set monochromatic.
Definition 1.16 (Homothetic copy).
Let
be a finite set of points in .
A homothetic copy of
is a set of the form .
Theorem 1.17 (Gallai’s Theorem).
Assuming that:
-
finite
-
-colouring
of
Proof.
.
Let
be a colouring.
We colour
(for
large enough) as follows:
|
|
By The Hales-Jewett Theorem, there exists a monochromatic combinatorial line in
with active
coordinates .
Then
has the same colour for all .
Done as this is a copy of
translate by ,
and dilation factor .
□