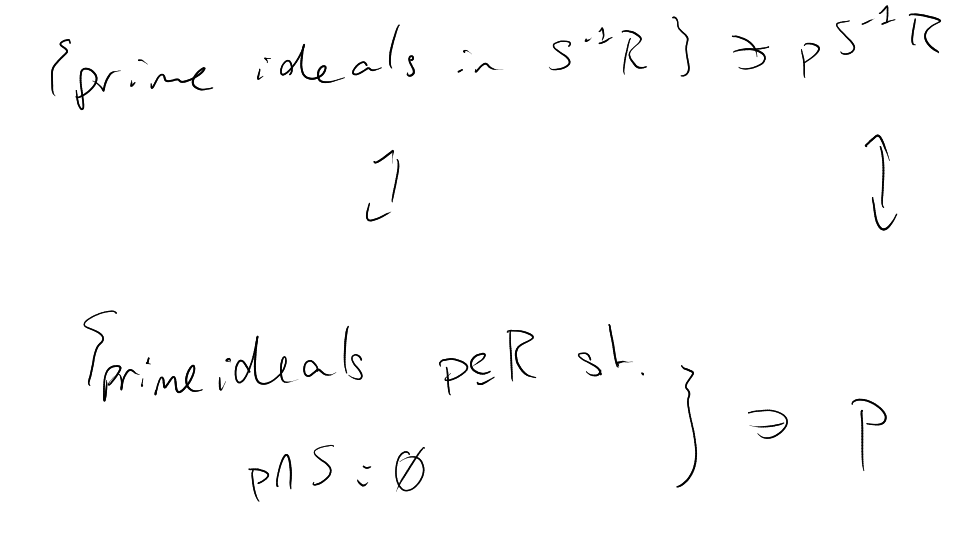Local Fields
Daniel Naylor

I Basic Theory
1Absolute values
2Valuation Rings
3The

p

-adic numbers

II  Complete Valued Fields
4Hensel’s Lemma
5Teichmüller lifts
6Extensions of complete valued fields

III  Local Fields
7Local Fields
8Global Fields

IV  Dedekind domains
9Dedekind domains
10Dedekind domains and extensions
10.1Completions
11Decomposition groups

V  Ramification Theory
12Different and discriminant
13Unramified and totally ramified extensions of local fields
13.1Structure of Units
14Higher Ramification Groups

VI  Local Class Field Theory
15Infinite Galois Theory
Index

Part I
Basic Theory

Example. $f (x_{1}, \dots, x_{r}) \in ℤ [c_{1}, \dots, x_{r}]$ , $f (x_{1}, \dots, x_{r}) = 0$ ? This is hard to study. It is easier to study

\begin{array}{l} f (x_{1}, \dots, x_{r}) & \equiv 0 (m o d p) \\ f (x_{1}, \dots, x_{r}) & \equiv 0 (m o d p^{2}) \\ ⋮ \\ f (x_{1}, \dots, x_{r}) & \equiv 0 (m o d p^{n}) \end{array}

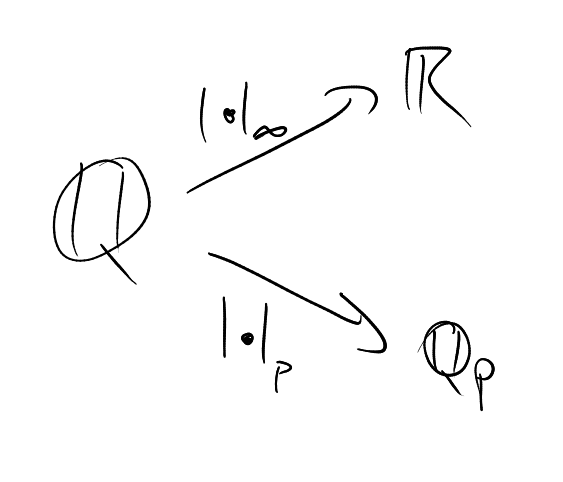
A local field packages all this information together.

1 Absolute values

Definition 1.1 (Absolute value). Let $K$ be a field. An absolute value on $K$ is a function $| ∙ | : K \to ℝ_{\geq 0}$ such that

(i) $| x | = 0$ if and only if $x = 0$ .
(ii) $| x y | = | x | | y |$ for all $x, y \in K$ .
(iii) $| x + y | \leq | x | + | y | \forall x, y \in K$ (triangly inequality).

We say $(K, | ∙ |)$ is a valued field.

Example.

$K = ℚ, ℝ, ℂ$ with usual absolute value $| a + i b | = \sqrt{a^{2} + b^{2}}$ . Write $| ∙ |_{\infty}$ for this absolute value.
$K$ any field. The trivial absolute value is
$| x | = {\begin{matrix} 0 & x = 0 \\ 1 & x \neq 0 \end{matrix}$

Although this is technically an absolute value, it is not useful or interesting, so should be ignored.

Definition 1.2 ( $p$ -adic absolute value). Let $K = ℚ$ , and $p$ be a prime. For $0 \neq x \in ℚ$ , write $x = p^{n} \frac{a}{b}$ , where $(a, p) = 1$ , $(b, p) = 1$ . The $p$ -adic absolute value is defined to be

| x |_{p} = {\begin{matrix} 0 & x = 0 \\ p^{- n} & x = p^{n} \frac{a}{b} \end{matrix}

Verification:

(i) Clear

(ii) Write

y = p^{m} \frac{c}{d}

. Then

{| x y |}_{p} = {| p^{m + n} \frac{a c}{b d} |}_{p} = p^{- m - n} = {| x |}_{p} {| y |}_{p} .

(iii) Without loss of generality, $m \geq n$ . Then
${| x + y |}_{p} = {| p^{n} \frac{a d + p^{m - n} b c}{b d} |}_{p} \leq p^{- n} = \max ({| x |}_{p}, {| y |}_{p}) .$

An absolute value $| ∙ |$ on $K$ induces a metric $d (x, y) = | x - y |$ on $K$ , hence a topology on $K$ .

Definition 1.3 (Place). Let $| ∙ |$ , ${| ∙ |}^{'}$ be absolute values on a field $K$ . We say $| ∙ |$ and ${| ∙ |}^{'}$ are equivalent if they induce the same topology. An equivalence class of absolute values is called a place.

Proposition 1.4. Assuming that:

$| ∙ |$ , ${| ∙ |}^{'}$ are (non-trivial) absolute values on $K$ .

Then the following are equivalent:

(i) $| ∙ |$ and ${| ∙ |}^{'}$ are equivalent.
(ii) $| x | < 1 ⟺ {| ∙ |}^{'} < 1$ for all $x \in K$ .
(iii) There exists $c \in ℝ_{> 0}$ such that ${| x |}^{c} = {| ∙ |}^{'}$ for all $x \in K$ .

Proof.

(i) $⟹$ (ii) $\begin{array}{l} | x | < 1 & ⟺ x^{n} \to 0 w.r.t | ∙ | \\ ⟺ x^{n} \to 0 w.r.t {| ∙ |}^{'} \\ ⟺ {| x |}^{'} < 1 \end{array}$

(ii)

⟹

(iii) Note:

{| x |}^{c} = {| x |}^{'} ⟺ c \log | x | = \log {| x |}^{'}

. Let

a \in K^{\times}

such that

| a | > 1

(exists since

| ∙ |

is non-trivial). We need that

\forall x \in K^{\times}

\frac{\log | x |}{\log | a |} = \frac{\log {| x |}^{'}}{\log {| a |}^{'}} .

Assume that

\frac{\log | x |}{\log | a |} < \frac{\log {| x |}^{'}}{\log {| a |}^{'}} .

Choose $m, n \in ℤ$ (with $n > 0$ ) such that

\frac{\log | x |}{\log | a |} < \frac{m}{n} < \frac{\log {| x |}^{'}}{\log {| a |}^{'}} .

Then we have

\begin{array}{l} n \log | x | & < m \log | a | \\ n \log {| x |}^{'} & > m \log {| a |}^{'} \end{array}

Hence $| \frac{x^{n}}{a^{m}} | < 1$ and $| \frac{x^{n}}{a^{m}} | > 1$ , contradiction. Similarly for the case where

\frac{\log | x |}{\log | a |} > \frac{\log {| x |}^{'}}{\log {| a |}^{'}} .

(iii) $⟹$ (i) Clear.

□

Remark. $| ∙ |_{\infty}^{2}$ on $ℂ$ is not an absolute value by our definition. Some authors replace the triangle inequality by

{| x + y |}^{β} \leq {| x |}^{β} + {| y |}^{β}

for some fixed $β \in ℝ_{> 0}$ .

Definition 1.5 (Non-archimedean). An absolute value $| ∙ |$ on $K$ is said to be non-archimedean if it satisfies the ultrametric inequality:

| x + y | \leq \max (| x |, | y |) .

If $| ∙ |$ is not non-archimedean, then it is archimedean.

Example.

${| ∙ |}_{\infty}$ on $ℝ$ is archimedean.
${| ∙ |}_{p}$ is a non-archimedean absolute value.

Lemma 1.6. Assuming that:

$(K, | ∙ |)$ is non-archimedean
$x, y \in K$
$| x | < | y |$

Then

| x - y | = | y |

Proof.

| x - y | \leq \max (| x |, | y |) = | y |

and

| y | \leq \max (| x |, | x - y |) \leq | x - y | .

□

Proposition 1.7. Assuming that:

$(K, | ∙ |)$ is non-archimedean
${(x_{n})}_{n = 1}^{\infty}$ a sequence in $K$
$| x_{n} - x_{n + 1} | \to 0$

Then

{(x_{n})}_{n = 1}^{\infty}

is Cauchy. In particular, if

K

is in addition complete, then

{(x_{n})}_{n = 1}^{\infty}

converges.

Proof. For $𝜀 > 0$ , choose $N$ such that $| x_{n} - x_{n + 1} | < 𝜀$ for $n > N$ . Then $N < n < m$ ,

| x_{n} - x_{m} | = | (x_{n} - x_{n + 1}) + \dots + (x_{n - 1}) - x_{m}) | < 𝜀 .

The “In particular” is clear. □

Example. $p = 5$ , construct sequence ${(x_{n})}_{n = 1}^{\infty}$ in $ℤ$ such that

(i) $x_{n}^{2} + 1 \equiv 0 (m o d 5^{n})$
(ii) $x_{n} \equiv x_{n + 1} (m o d 5^{n})$

Take $x_{1} = 2$ . Suppose we have constructed $x_{n}$ . Let $x_{n}^{2} + 1 = a 5^{n}$ and set $x_{n + 1} = x_{n} + b 5^{n}$ . Then

\begin{array}{l} x_{n + 1}^{2} + 1 & = x_{n}^{2} + 2 b x_{n} 5^{n} + b^{2} 5^{2 n} + 1 \\ = a 5^{n} + 2 b x_{n} 5^{n} + b^{2} 5^{2 n} \end{array}

We choose $b$ such that $a + 2 b x_{n} \equiv 0 (m o d 5)$ . Then we have $x_{n + 1}^{2} + 1 \equiv 0 (m o d 5^{n + 1})$ . Now (ii) implies that ${(x_{n})}_{n = 1}^{\infty}$ is Cauchy. Suppose $x_{n} \to l \in ℚ$ . Then $x_{n}^{2} \to l^{2}$ . But (i) tells us that $x_{n}^{2} \to - 1$ , so $l^{2} = - 1$ , a contradiction. Thus $(ℚ, {| ∙ |}_{5})$ is not complete.

Definition 1.8. The $p$ -adic numbers $ℚ_{p}$ is the completion of $ℚ$ with respect to ${| ∙ |}_{p}$ .

Analogy with $ℝ$ :

Notation. As is usual when working with metric spaces, we will be using the notation:

\begin{array}{l} B (x, r) & = {y \in K | | x - y | < r} \\ \bar{B} (x, r) & = {y \in K | | x - y | \leq r} \end{array}

Lemma 1.9. Assuming that:

$(K, | ∙ |)$ is a non-archimedean valued field

Then

(i) If $z \in B (x, r)$ , then $B (z, r) = B (x, r)$ – so open balls don’t have a centre.
(ii) If $z \in \bar{B} (x, r)$ then $\bar{B} (x, r) = \bar{B} (z, r)$ .
(iii) $B (x, r)$ is closed.
(iv) $\bar{B} (x, r)$ is open.

Proof.

(i) Let $y \in B (x, r)$ . Then $| x - y | < r$ hence $\begin{array}{l} | z - y | & = | (z - x) + (x - y) | \\ \leq \max (| z - x |, | x - y |) \\ < r \end{array}$
Thus $B (x, r) \subseteq B (z, r)$ . $\supseteq$ follows by symmetry.
(ii) Same as (i).
(iii) Let $y \notin B (x, r)$ . If $z \in B (x, r) \cap B (y, r)$ then $B (x, r) = B (z, r) = B (y, r)$ Hence $y \in B (x, r)$ . Hence $B (x, r) \cap B (y, r) = \emptyset$ .
(iv) If $z \in \bar{B} (x, r)$ , then $B (z, r) \subseteq \bar{B} (z, r) = \bar{B} (x, r)$ . □

2 Valuation Rings

Definition 2.1 (Valuation). Let $K$ be a field. A valuation on $K$ is a function $v : K^{\times} \to ℝ$ such that

(i) $v (x y) = v (x) + v (y)$
(ii) $v (x + y) \geq \min (v (x), v (y))$

Fix $0 < α < 1$ . If $v$ is a valuation on $K$ , then

| x | = {\begin{matrix} α^{v (x)} & x \neq 0 \\ 0 & x = 0 \end{matrix}

determines a non-archimedean absolute value on $K$ .

Conversely a non-archimedean absolute value determines a valuation $v (x) = \log_{α} | x |$ .

Remark.

Ignore the trivial valuation $v (x) = 0$ .
Say $v_{1}, v_{2}$ are equivalent if there exists $c \in ℝ > 0$ such that $v_{1} (x) = c v_{2} (x)$ for all $x \in K^{\times}$ .

Example.

$K = ℚ$ , $v_{p} (x) = - \log_{p} {| x |}_{p}$ is known as the $p$ -adic valuation.
If $k$ is a field, consider $K = k (t) = Frac (k [t])$ the rational function field. Then define
$v (t^{n} \frac{f (t)}{g (t)}) = n$

for $f, g \in k [t]$ with $f (0), g (0) \neq 0$ . We call this the $t$ -adic valuation.

$K = k ((t)) = Frac (k [[t]]) = {\sum_{i = n}^{\infty} a_{i} t^{i} | a_{i} \in k, n \in ℤ}$ , known as the field of formal Laurent series over $k$ . Then we can define

v (\sum_{I} a_{i} t^{i}) = \min {i | a_{i} \neq 0}

is the $t$ -adic valuation on $K$ .

Definition 2.2. Let $(K, | ∙ |)$ be a non-archimedean valued field. The valuation ring of $K$ is defined to be

\begin{array}{l} O_{K} & = {x \in K | | x | \leq 1} (= \bar{B} (0, 1)) \\ ( & = {x \in K^{\times} | v (x) \geq 0} \cup {0}) \end{array}

Proposition 2.3.

(i) $O_{K}$ is an open subring of $K$
(ii) The subsets ${x \in K | | x | \leq r}$ and ${x \in K | | x | < r}$ for $r \leq 1$ are open ideals in $O_{K}$ .
(iii) $O_{K}^{\times} = {x \in K | | x | = 1}$ .

Proof.

(i) $| 0 | = 0$ , $| 1 | = 1$ so $0, 1 \in O_{K}$ . If $x \in O_{K}$ , then $| - x | = | x |$ hence $- x \in O_{K}$ . If $x, y \in O_{K}$ , then
$| x + y | \leq \max (| x |, | y |) \leq 1 .$

Hence $x + y \in O_{K}$ . If $x, y \in O_{K}$ , then $| x y | = | x | | y | \leq 1$ , hence $x y \in O_{K}$ . Thus $O_{K}$ is a ring. Since $O_{K} = \bar{B} (0, 1)$ , it is open.
(ii) Similar to (i).
(iii) Note that $| x | | x^{- 1} | = | x x^{- 1} | = 1$ . Thus $\begin{array}{l} | x | = 1 & ⟺ | x^{- 1} | = 1 \\ ⟺ x, x^{- 1} \in O_{K} \\ ⟺ x \in O_{K}^{\times} □ \end{array}$

Notation.

$m : = {x \in O_{K} | | x | < 1}$ is a max ideal of $O_{K}$ .
$k : = O_{K} ∕ m$ is the residue field.

Corollary 2.4. $O_{K}$ is a local ring with unique maximal ideal $m$ (a local ring is a ring with a unique maximal ideal).

Proof. Let $m^{'}$ be a maximal ideal. Suppose $m^{'} \neq m$ . Then there exists $x \in m^{'} ∖ m$ . Using part (iii) of Proposition 2.3, we get that $x$ is a unit, hence $m^{'} = O_{K}$ , a contradiction. □

Example. $K = ℚ$ with ${| ∙ |}_{p}$ . Then

O_{K} = ℤ_{(p)} = {\frac{a}{b} \in ℚ | p ∤ b},

and $m = p ℤ_{(p)}$ , $k = 𝔽_{p}$ .

Definition 2.5. Let $v : K^{\times} \to ℝ$ be a valuation. If $v (K^{\times}) ≅ ℤ$ , we say $v$ is a discrete valuation. $K$ is said to be a discretely valued field. An element $π \in O_{K}$ is uniformiser if $v (π) > 0$ and $v (π)$ generates $v (K^{\times})$ .

Example.

$K = ℚ$ with $p$ -adic valuation is a discrete valuation ring.
$K = k (t)$ with $t$ -adic valuation is a discrete valuation ring.
$K = k (t) (t^{1 ∕ 2}, t^{1 ∕ 4}, t 1 ∕ 8, \dots)$ . Here, the $t$ -adic valuation is not discrete.

Remark. If $v$ is a discrete valuation, can replace with equivalent one such that $v (K^{\times}) = ℤ$ > Call such a $v$ normalised valuations (then $v (π) = 1$ if and only if $π$ is a unit).

Lemma 2.6. Assuming that:

$v$ is a valuation on $K$

Then the following are equivalent:

(i) $v$ is discrete
(ii) $O_{K}$ is a PID
(iii) $O_{K}$ is Noetherian
(iv) $m$ is principal

Proof.

(i)

⟹

(ii)

O_{K}

is an integral domain since it is a subset of

K

, which is an integral domain.

Let $I \subseteq O_{K}$ be a non-zero ideal. Let $x \in I$ such that $v (x) = \min {v (a) | a \in I}$ , which exists since $v$ is discrete. Then we claim

x O_{K} = {a \in O_{K} | v (a) \geq v (x)}

is equal to $I$ .

$\subseteq$ ( $I$ is an ideal)
$\supseteq$ Let $y \in I$ . Then $v (x^{- 1} y) \geq 0$ . Hence $y = x (x^{- 1} y) \in x O_{K}$ .

(ii) $⟹$ (iii) Clear.
(iii) $⟹$ (iv) Write $m = x_{1} O_{K} + \dots + x_{n} O_{K}$ . Without loss of generality,
$v (x_{1}) \leq v (x_{2}) \leq \dots \leq v (x_{n}) .$

Then $x_{2}, \dots, x_{n} \in x_{1} O_{K}$ . Hence $m = x_{1} O_{K}$ .
(iv) $⟹$ (i) Let $m = π O_{K}$ for some $π \in O_{K}$ and let $c = v (π)$ . Then if $v (x) > 0$ , $x \in m$ hence $v (x) \geq c$ . Thus $v (K^{\times}) \cap (0, c) = \emptyset$ . Since $v (K^{\times})$ is a subgroup of $(ℝ, +)$ , we deduce $v (K^{\times}) = ℤ$ . □

Suppose $v$ is a discrete valuation on $K$ , $π \in O_{K}$ a uniformiser. For $x \in K^{\times}$ , let $n \in ℤ$ such that $v (x) = n v (π)$ . Then $u = π^{- n} x \in O_{K}^{\times}$ and $x = u π^{n}$ . In particular, $K = O_{K} [\frac{1}{π}]$ and hence $K = Frac (O_{K})$ .

Definition 2.7 (Discrete valuation ring). A ring $R$ is called a discrete valuation ring (DVR) if it is a PID with exactly one non-zero prime ideal (necessarily maximal).

Lemma 2.8.

(i) Let $v$ be a discrete valuation on $K$ . Then $O_{K}$ is a discrete valuation ring.
(ii) Let $R$ be a discrete valuation ring. Then there exists a valuation on $K : = Frac (R)$ such that $R = O_{K}$ .

Proof.

(i) $O_{K}$ is a PID by Lemma 2.6. Hence any non-zero prime ideal is maximal and hence $O_{K}$ is a discrete valuation ring since it is a local ring.
(ii) Let $R$ be a discrete valuation ring, with maximal ideal $m$ . Then $m = (π)$ for some $π \in R$ . Since PIDs are UFDs, we may write any $x \in R ∖ {0}$ uniquely as $π^{n} u$ with $n \geq 0$ , $u \in R^{\times}$ . Then any $y \in K^{\times}$ can be written uniquely as $π^{m} u$ with $u \in R^{\times}$ , $m \in ℤ$ . Define $v (π^{m} u) = m$ ; check $v$ is a valuation and $O_{K} = R$ . □

Example. $ℤ_{(p)}$ , $k [[t]]$ ( $k$ a field) are discrete valuation rings.

3 The $p$ -adic numbers

Recall that $ℚ_{p}$ is the completion of $ℚ$ with respect to ${| ∙ |}_{p}$ . On Example Sheet 1, we will show that $ℚ_{p}$ is a field. We also show that ${| ∙ |}_{p}$ extends to $ℚ_{p}$ and the associated valuation is discrete.

Definition 3.1. The ring of $p$ -adic integers $ℤ_{p}$ is the valuation ring

ℤ_{p} = {x \in ℚ_{p} | {| x |}_{p} \leq 1} .

Facts: $ℤ_{p}$ is a discrete valuation ring, with maximal ideal $p ℤ_{p}$ , and non-zero ideals are given by $p^{n} ℤ_{p}$ .

Proposition. $ℤ_{p}$ is the closure of $ℤ$ inside $ℚ_{p}$ . In particular, $ℤ_{p}$ is the completion of $ℤ$ with respect to ${| ∙ |}_{p}$ .

Proof. Need to show $ℤ$ is dense in $ℤ_{p}$ . Note $ℚ$ is dense in $ℚ_{p}$ . Since $ℤ_{p} \subseteq ℚ_{p}$ is open, we have that $ℤ_{p} \cap ℚ$ is dense in $ℤ_{p}$ . Now:

ℤ_{p} \cap ℚ = {x \in ℚ | {| x |}_{p} \leq 1} = {\frac{a}{b} \in ℚ | p ∤ b} = ℤ_{(p)} .

Thus it suffices to show $ℤ$ is dense in $ℤ_{(p)}$ .

Let $\frac{a}{b} \in ℤ_{(p)}$ , $a, b \in ℤ$ , $p ∤ b$ . For $n \in ℕ$ , choose $y_{n} \in ℤ$ such that $b y_{n} \equiv a (m o d p^{n})$ . THen $y_{n} \to \frac{a}{b}$ as $n \to \infty$ .

In particular, $ℤ_{p}$ is complete and $ℤ \subseteq ℤ_{p}$ is dense. □

Definition (Inverse limit). Let ${(A_{n})}_{n = 1}^{\infty}$ be a sequence of sets / groups / rings together with homomorphisms $φ_{n} : A_{n + 1} \to A_{n}$ (transition maps). Then the inverse limit of ${(A_{n})}_{n = 1}^{\infty}$ is the set / group / ring defined by

\lim_{\overset{[}{n}] \leftarrow} A_{n} = {{(a_{n})}_{n = 1}^{\infty} \in \prod_{n = 1}^{\infty} A_{n} | φ (a_{n + 1}) = a_{n} \forall n} .

Define the group / ring operation componentwise.

Notation. Let $𝜃_{m} : \lim_{\overset{[}{n}] \leftarrow} A_{n} \to A_{m}$ denote the natural projection.

The inverse limit satisfies the following universal property:

Proposition 3.2 (Universal property of inverse limits). Assuming that:

$B$ is a set / group / ring
$ψ_{n}$ are homomorphisms $ψ_{n} : B \to A_{n}$ such that
commutes for all $n$

Then there exists a unique homomorphism

ψ : B \to \lim_{\overset{[}{n}] \leftarrow} A_{n}

such that

𝜃_{n} \circ ψ = ψ_{n}

Proof. Define

\begin{array}{l} ψ : B & \to \prod_{n = 1}^{\infty} A_{n} \\ b & \mapsto \prod_{n = 1}^{\infty} ψ_{n} (b) \end{array}

Then $ψ_{n} = φ_{n} \circ ψ_{n + 1}$ implies that $ψ (b) \in \lim_{\overset{[}{n}] \leftarrow} A_{n}$ . The map is clearly unique (determined by $ψ_{n} = 𝜃_{n} \circ ψ$ ) and is a homomorphism of sets / groups / rings. □

Definition 3.3 ( $I$ -adic completion). Let $I \subseteq R$ be an ideal ( $R$ a ring). The $I$ -adic completion of $R$ is the

\hat{R} : = \lim_{\overset{[}{R}] \leftarrow} ∕ I^{n}

where $R ∕ I^{n + 1} \to R ∕ I^{n}$ is the natural projection.

Note that there exists a natural map $i : R \to \hat{R}$ by the Universal property of inverse limits (there exist maps $R \to R ∕ I^{n}$ ). We say $R$ is $I$ -adically complete if it is an isomorphism.

Fact: $\ker (i : R \to \hat{R}) = ⋂_{n = 1}^{\infty} I^{n}$ .

Let $(K, | ∙ |)$ be a non-archimedean valued fieldand $π \in O_{K}$ such that $| π | < 1$ .

Proposition 3.4. Assuming that:

$K$ is complete with respect to $| ∙ |$

Then

(i) Then $O_{K} ≅ \lim_{\overset{[}{n}] \leftarrow} O_{K} ∕ π^{n} O_{K}$ ( $O_{K}$ is $π$ -adically complete)
(ii) Every $x \in O_{K}$ can be written uniquely as $x = \sum_{i = 0}^{n} a_{i} π^{i}$ , $a_{i} \in A$ , where $A \subseteq O_{K}$ is a set of coset representatives for $O_{K} ∕ π O_{K}$ .

Proof.

(i) $K$ is complete and $O_{K}$ is closed, so $O_{K}$ is complete.
$x \in ⋂_{n = 1}^{\infty} π^{n} O_{K}$ impies $v (x) \geq n v (π)$ for all $n$ , and hence $x = 0$ . Hence $O_{K} \to {\lim_{\overset{[}{O}] \leftarrow}}_{K} ∕ π^{n} O_{K}$ is injective.

Let ${(x_{n})}_{n = 1}^{\infty} \in {\lim_{\overset{[}{O}] \leftarrow}}_{K} ∕ π^{n} O_{K}$ and for each $n$ , let $y_{n} \in O_{K}$ be a lifting of $x_{n} \in O_{K} ∕ π^{n} O_{K}$ . Then $y_{n} - y_{n + 1} \in π^{n} O_{K}$ so that $v (y_{n} - y_{n + 1}) \geq n v (π)$ .

Thus ${(y_{n})}_{n = 1}^{\infty}$ is a Cauchy sequence in $O_{K}$ . Let $y_{n} \to y \in O_{K}$ . Then $y$ maps to ${(x_{n})}_{n = 1}^{\infty}$ in the $\lim_{\overset{[}{n}] \leftarrow} O_{K} ∕ π^{n} O_{K}$ . Thus $O_{K} \to \lim_{\overset{[}{n}] \leftarrow} O_{K} ∕ π^{n} O_{K}$ is surjective.
(ii) Exercise on Example Sheet 1. □

Corollary 3.5.

(i) $ℤ_{p} ≅ \lim_{\overset{[}{ℤ}] \leftarrow} ∕ p^{n} ℤ$ .
(ii) Every element $x \in ℚ_{p}$ can be written uniquely as
$x = \sum_{i = n}^{\infty} a_{i} p^{i},$

with $n \in ℤ$ , $a_{i} \in {0, 1, \dots, - 1}$ .

Proof.

(i) It suffices by Proposition 3.4 to show that

ℤ_{p} ∕ p^{n} ℤ_{p} ≅ ℤ ∕ p^{n} ℤ .

Let $f_{n} : ℤ \to ℤ_{p} ∕ p^{n} ℤ_{p}$ be the natural map

\ker (f_{n}) = {x \in ℤ | {| x |}_{p} \leq p^{- n}} = p^{n} ℤ,

hence $ℤ ∕ p^{n} ℤ \to ℤ_{p} ∕ p^{n} ℤ_{p}$ is injective.

Let $τ \in ℤ_{p} ∕ p^{n} ℤ_{p}$ and let $c \in ℤ_{p}$ be a lift. Since $ℤ$ is dense in $ℤ_{p}$ , there exists $x \in ℤ$ such that $x \in c + p^{n} ℤ_{p}$ is open in $ℤ_{p}$ . Then $f_{n} (x) = τ$ , hence $ℤ ∕ p^{n} ℤ \to ℤ_{p} ∕ p^{n} ℤ_{p}$ is surjective.

(ii) It follows from Proposition 3.4(ii) to $p^{- n} x \in ℤ_{p}$ for some $n \in ℤ$ □

Example.

\frac{1}{1 - p} = 1 + p + p^{2} + p^{3} + \dots

Part II
Complete Valued Fields

4 Hensel’s Lemma

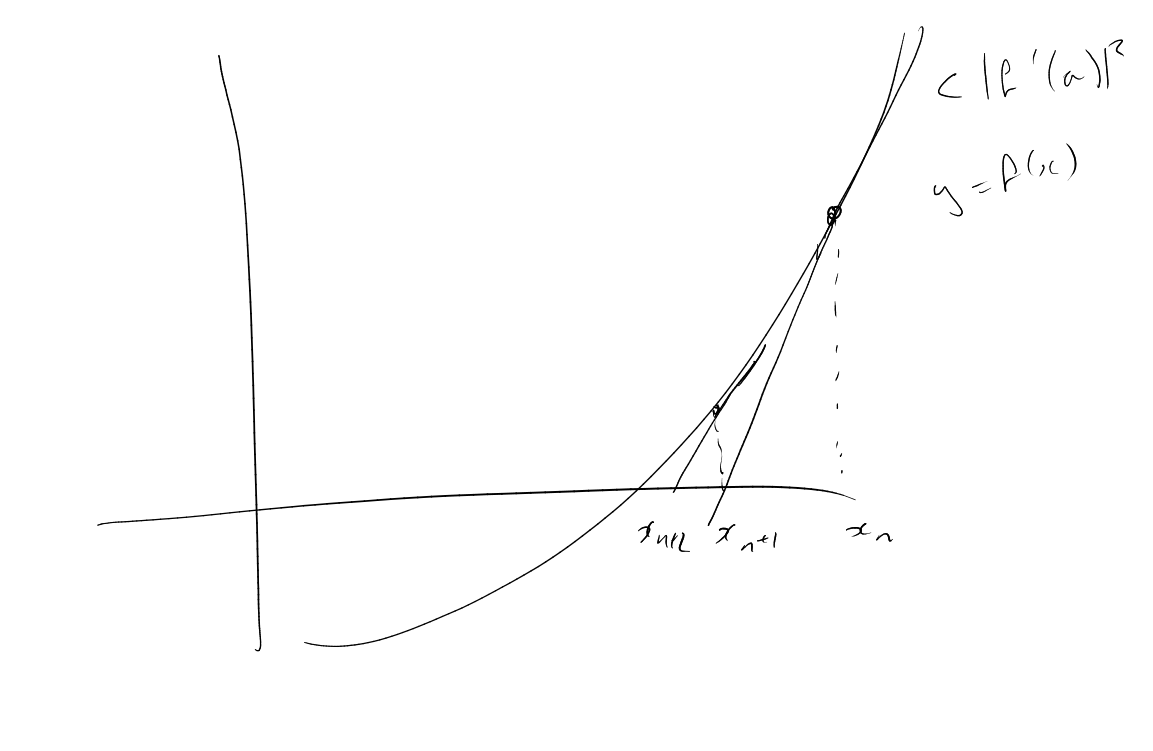
Theorem 4.1 (Hensel’s Lemma version 1). Assuming that:

$(K, | ∙ |)$ is a complete discretely valued field
$f (X) \in O_{K} [X]$
assume $\exists a \in O_{K}$ such that $| f (a) | < | f^{'} (a) |^{2}$

Then there exists a unique

x \in O_{K}

such that

f (x) = 0

and

| x - a | < | f^{'} (a) |

Proof. Let $π \in O_{K}$ be a uniformiser and let $r = v (f^{'} (a))$ , with $v$ the normalised valuation ( $v (π) = 1$ ). We construct a sequence ${(x_{n})}_{n = 1}^{\infty}$ in $O_{K}$ such that:

(i) $f (x_{n}) \equiv 0 (m o d π^{n + 2 r})$
(ii) $x_{n + 1} \equiv x_{n} (m o d π^{n + r})$

Take $x_{1} = a$ : then $f (x_{1}) \equiv 0 (m o d π 1 + 2 r)$ .

Now we suppose we have constructed $x_{1}, \dots, x_{n}$ satisfying (i) and (ii). Define

x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})} .

Since $x_{n} \equiv x_{1} (m o d π^{r + 1})$ , we have

v (f^{'} (x_{n})) = v (f^{'} (x_{i})) = r,

and hence

\frac{f (x_{n})}{f^{'} (x_{n})} \equiv 0 (m o d π^{n + r})

by (i).

It follows that $x_{n + 1} \equiv x_{n} (m o d π^{n + r})$ , so (ii) holds. Note that letting $X, Y$ be indeterminates, we have

f (X + Y) = f_{0} (X) + f_{1} (X) Y + f_{2} (X) Y^{2} + \dots,

where $f_{i} (X) \in O_{K} [X]$ and $f_{0} (X) = f (X)$ , $f_{1} (X) = f^{'} (X)$ . Thus

f (x_{n + 1}) = f (x_{n}) + c f^{'} (x_{n}) + c^{2} f_{2} (x_{N}) + \underset{\in π^{n + 2 r + 1}}{\underset{⏟}{c^{2} f_{2} (x_{n}) + \dots}}

where $c = - \frac{f (x_{n})}{f^{'} (x_{n})}$ .

Since $c \equiv 0 (m o d π^{n + r})$ and $v (f_{i} (x_{n})) \geq 0$ we have

f (x_{n + 1}) \equiv f (x_{n}) + f^{'} (x_{n}) c \equiv 0 (m o d π^{n + 2 r + 1}),

so (i) holds.

Property (ii) implies that ${(x_{n})}_{n = 1}^{\infty}$ is Cauchy, so let $x \in O_{K}$ such that $x_{n} \to x$ . Then $f (x) = \lim_{n \to \infty} f (x_{n}) = 0$ by (i).

Moreover, (ii) impies that

\begin{array}{l} a = x_{1} & \equiv x_{n} (m o d π^{r + 1}) \forall n \\ ⟹ a & \equiv x (m o d π^{r + 1}) \\ ⟹ | x - a | & < | f^{'} (a) | \end{array}

This proves existence.

Uniqueness: suppose $x^{'}$ also satisfies $f^{'} (x) = 0$ , $| x^{'} - a | < | f^{'} (a) |$ . Set $δ = x^{'} - x \neq 0$ . Then

| x^{'} - a | < | f^{'} (a) | | x - a^{'} | < | f^{'} (a) |,

and the ultrametric inequality implies

| δ | = | x - x^{'} | < | f^{'} (a) | = | f^{'} (x) | .

But

0 = f (x^{'}) = f (x + δ) = \underset{= 0}{\underset{⏟}{f (x)}} + f^{'} (x) δ + \underset{| ∙ | \leq | δ |^{2}}{\underset{⏟}{\dots}} .

Hence $| f^{'} (x) δ | \leq | δ |^{2}$ , so $| f^{'} (x) | < | δ |$ , a contradiction. □

Corollary 4.2. Let $(K, | ∙ |)$ be a complete discretely valued field. Let $f (X) \in O_{K} [X]$ and $\bar{c} \in k : = O_{K} ∕ m$ a simple root of $\bar{f} (X) : = f (X) (m o d m) \in k [X]$ . Then there exists a unique $x \in O_{K}$ such that $f (x) = 0$ , $x \equiv \bar{c} (m o d m)$ .

Proof. Apply Theorem 4.1 to a lift $c \in O_{K}$ of $\bar{c}$ . Then $| f (c) | < 1 = | f^{'} (c) |^{2}$ since $\bar{c}$ is a simple root. □

Example. $f (X) = X^{2} - 2$ has a simple root modulo 7. Thus $\sqrt{2} \in ℤ_{7} \subseteq ℚ_{7}$ .

Corollary 4.3.

{ℚ_{p}}^{\times} ∕ {({ℚ_{p}}^{\times})}^{2} ≅ {\begin{matrix} {(ℤ ∕ 2 ℤ)}^{2} & if p > 2 \\ {(ℤ ∕ 2 ℤ)}^{3} & if p = 2 \end{matrix}

Proof. Case $p > 2$ : Let $b \in {ℤ_{p}}^{\times}$ . Applying to $f (X) = X^{2} - b$ , we find that $b \in {({ℤ_{p}}^{\times})}^{2}$ if and only if $b \in {(𝔽_{p}^{\times})}^{2}$ . Thus ${ℤ_{p}}^{\times} ∕ {({ℤ_{p}}^{\times})}^{2} ≅ 𝔽_{p}^{\times} ∕ {(𝔽_{p}^{\times})}^{2} ≅ ℤ ∕ 2 ℤ$ ( $𝔽_{p}^{\times} ≅ ℤ ∕ (p - 1) ℤ$ ).

We have an isomorphism

{ℤ_{p}}^{\times} \times (ℤ, +) ≅ {ℚ_{p}}^{\times}

given by $(u, n) \mapsto u p^{n}$ . Thus

{ℚ_{p}}^{\times} ∕ {({ℚ_{p}}^{\times})}^{2} ≅ {(ℤ ∕ 2 ℤ)}^{2} .

Case $p = 2$ : Let $b \in ℤ_{2}^{\times}$ . Consider $f (X) = X^{2} - b$ . Note $f^{'} (X) = 2 X \equiv 0 (m o d 2)$ . Let $b \equiv 1 (m o d 8)$ . Then

| f (1) | = 2^{- 3} < 2^{- 2} = | f^{'} (1) |^{2} .

Hensel’s Lemma version 1 gives

b \in {(ℤ_{2}^{\times})}^{2} ⟺ b \equiv 1 (m o d 8) .

Then

ℤ_{2}^{\times} ∕ {(ℤ_{2}^{\times})}^{2} ≅ {(ℤ ∕ 8 ℤ)}^{\times} \equiv {(ℤ ∕ 2 ℤ)}^{j} .

Again using $ℚ_{2}^{\times} \equiv ℤ_{2}^{\times} \times ℤ$ , we find that $ℚ_{2}^{\times} ≅ {(ℤ ∕ 2 ℤ)}^{3}$ . □

Remark. Proof uses the iteration

x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})},

which is the non-archimedean analogue of the unewton Raphson method.

Theorem 4.4 (Hensel’s Lemma version 2). Assuming that:

$(K, | ∙ |)$ is a complete discretely valued field
$f (X) \in O_{K} [X]$
$\bar{f} (X) : = f (X) (m o d m) \in k [X]$ factorises as $\bar{f} (X) = \bar{g} (X) \bar{h} (X)$ in $k [X]$
$\bar{g} (X)$ and $\bar{h} (X)$ coprime.

Then there is a factorisation

f (X) = g (X) h (X)

in $O_{K} [X]$ , with $\bar{g} (X) \equiv g (X) (m o d m)$ , $\bar{h} (X) \equiv h (X) (m o d m)$ and $\deg \bar{g} = \deg g$ .

Proof. Example Sheet 1. □

Corollary 4.5. Let $(K, | ∙ |)$ be a complete discretely valued field. Let

f (X) = a_{n} X^{n} + \dots + a_{n} \in K [X]

with $a_{0}, a_{n} \neq 0$ . If $f (X)$ is irreducible, then $| a_{i} | \leq \max (| a_{0} |, | a_{n} |)$ for all $i$ .

Proof. Upon scaling, we may assume $f (X) \in O_{K} [X]$ with $\max_{i} (| a_{i} |) = 1$ . Thus we need to show that $\max (| a_{0} |, | a_{n} |) = 1$ . If not, let $r$ minimal such that $| a_{r} | = 1$ , then $0 < r < n$ . Thus we have

\bar{f} (X) = X^{r} (a_{r} + \dots + a_{n} X^{n - r}) (m o d m) .

Then Theorem 4.4 implies $f (X) = g (X) h (X)$ with $0 < \deg < n$ . □

5 Teichmüller lifts

Definition 5.1 (Perfect). A ring $R$ of characteristic $p > 0$ (prime) is a perfect ring if the Frobenius $x \mapsto x^{p}$ is a bijection. A field of characteristic $p$ is a perfect field if it is perfect as a ring.

Remark. Since $characteristic R = p$ , ${(x + y)}^{p} = x^{p} + y^{p}$ , so Frobenius is a ring homomorphism.

Example.

(i) $𝔽_{p^{n}}$ and $\bar{𝔽_{p}}$ are perfect fields.
(ii) $𝔽_{p} [t]$ is not perfect, because $t \notin Im (Frob)$ .
(iii) $𝔽_{p} (t^{\frac{1}{p^{\infty}}}) : = 𝔽_{p} (t, t^{\frac{1}{p}}, t^{\frac{1}{p^{2}}}, \dots)$ is a perfect field (called the perfection of $𝔽_{p} (t)$ ).

Fact: A field of characteristic $p > 0$ is perfect if and only if any finite extension of $k$ is separable.

Theorem 5.2. Assuming that:

$(K, | ∙ |)$ is a complete discretely valued field
such that $k : = O_{K} ∕ m$ is a perfect field of characterist $p$

Then there exists a unique map

[∙] : k \to O_{K}

such that

(i) $a \equiv [a] mod m$ for all $a \in k$
(ii) $[a b] = [a] [b]$ for all $a, b \in k$

Moreover if $characteristic O_{K} = p$ , then $[∙]$ is a ring homomorphism.

Definition 5.3. The element $[a] \in O_{K}$ constructed in Theorem 5.2 is the Teichmüller lift of $a$ .

Lemma 5.4. Assuming that:

$(K, | ∙ |)$ is a complete discretely valued field
such that $k : = O_{K} ∕ m$ is a perfect field of characterist $p$
$π \in O_{K}$ a fixed uniformiser
$x, y \in O_{K}$ such that $x \equiv y mod π^{k}$ ( $k \geq 1$ )

Then

x^{p} \equiv y^{p} mod π^{k + 1}

Proof. Let $x = y + u π^{k}$ with $u \in O_{K}$ . Then

\begin{array}{l} x^{p} & = \sum_{i = 0}^{p} (\binom{p}{i}) y^{p - i} {(u π^{k})}^{i} \\ = y^{p} + \sum_{i = 1}^{p} (\binom{p}{i}) y^{p - 1} {(u π^{k})}^{i} \end{array}

Since $O_{K} ∕ π O_{K}$ has characteristic $p$ , we have $p \in π O_{K}$ . Thus

(\binom{p}{i}) {(u π^{k})}^{i} y^{p - i} \in π^{k + 1} O_{K} \forall i \geq 1,

hence $x^{p} \equiv y^{p} mod π^{k + 1}$ . □

Proof of Theorem 5.2. Let $a \in k$ . For each $i \geq 0$ we choose a lift $y_{i} \in O_{K}$ of $a^{\frac{1}{p^{i}}}$ , and we define

x_{i} : = y_{i}^{p_{i}} .

We claim that ${(x_{i})}_{i = 1}^{\infty}$ is a Cauchy sequence and its limit is independent of the choice of $y_{i}$ .

By construction, $y_{i} \equiv y_{i + 1}^{p} mod π$ . By Lemma 5.4 and induction on $k$ , we have $y_{i}^{p^{k}} \equiv y_{i + 1}^{p^{k + 1}}$ and hence $x_{i} \equiv x_{i + 1} mod π^{i + 1}$ (take $i = p$ ). Hence ${(x_{i})}_{i = 1}^{\infty}$ is Cauchy, so $x_{i} \to x \in O_{K}$ .

Suppose ${(x_{i}^{'})}_{i = 1}^{\infty}$ arises from another choice of $y_{i}^{'}$ lifting $a_{i}^{\frac{1}{p^{i}}}$ . Then ${(x_{i}^{'})}_{i = 1}^{\infty}$ is Cauchy, and $x_{i}^{'} \to x^{'} \in O_{K}$ . Let

x_{i}^{″} = {\begin{matrix} x_{i} & i even \\ x_{i}^{'} & i odd \end{matrix} .

Then $x_{i}^{″}$ arises from lifting

y_{i}^{″} = {\begin{matrix} y_{i} & i even \\ y_{i} & i odd \end{matrix} .

Then $x_{i}^{″}$ is Cauchy and $x_{i}^{″} \to x$ , $x_{i}^{″} \to x^{'}$ . So $x = x^{'}$ and hence $x$ is independet of the choice of $y_{i}$ . So we may define $[a] = x$ .

Then $x_{i} = y_{i}^{p^{i}} \equiv {(a^{\frac{1}{p^{i}}})}^{p^{i}} \equiv a mod π$ . Hence $x \equiv a mod π$ . So (i) is satisfied.

We let $b \in k$ and we choose $u_{i} \in O_{K}$ a lift of $b^{\frac{1}{p^{i}}}$ , and let $z_{i} : = u_{i}^{p^{i}} t$ . Then $\lim_{i \to \infty} z_{i} = [b]$ .

Now $u_{i} y_{i}$ is a lift of ${(a b)}^{\frac{1}{p^{i}}}$ , hence

[a b] = \lim_{i \to \infty} x_{i} z_{i} = (\lim_{i \to \infty} x_{i}) (\lim_{i \to \infty} z_{i}) = [a] [b] .

So (ii) is satisfied.

If $characteristic K = p$ , $y_{i} + u_{i}$ is a lift of $a^{\frac{1}{p^{i}}} + b^{\frac{1}{p^{i}}} = {(a + b)}^{\frac{1}{p^{i}}}$ . Then

\begin{array}{l} [a + b] & = \lim_{i \to \infty} {(y_{i} + u_{i})}^{p^{i}} \\ = \lim_{i \to \infty} y_{i}^{p^{i}} + u_{i}^{p^{i}} \\ = \lim_{i \to \infty} x_{i} + z_{i} \\ = [a] + [b] \end{array}

Easy to check that $[0] = 0$ , $[1] = 1$ , and hence $[∙]$ is a ring homomorphism.

Uniqueness: let $ϕ : k \to O_{K}$ be another such map. Then for $a \in k$ , $ϕ (a^{\frac{1}{p^{i}}})$ is a lift of $a^{\frac{1}{p^{i}}}$ . It follows that

\begin{array}{l} [a] & = \lim_{i \to \infty} ϕ {(a^{\frac{1}{p^{i}}})}^{p^{i}} \\ = \lim_{i \to \infty} ϕ (a) \\ = ϕ (a) □ \end{array}

Example. $K = ℚ_{p}$ , $[∙] : 𝔽_{p} \to ℤ_{p}$ , $a \in 𝔽_{p}^{\times}$ , ${[a]}^{p - 1} = [a^{p - 1}] = [1] = 1$ . So $[a]$ is a $(p - 1)$ -th root of unity.

Lemma 5.5. Assuming that:

$(K, | ∙ |)$ complete discretely valued field
$k = O_{K} ∕ m \subseteq \bar{𝔽_{p}}$
$a \in k^{\times}$

Then

[a]

is a root of unity.

Proof.

\begin{array}{l} a \in k^{\times} & ⟹ a \in 𝔽_{p^{n}}^{\times} for some n \\ ⟹ {[a]}^{p^{n} - 1} = [a^{p^{n} - 1}] = [1] = 1 □ \end{array}

Theorem 5.6. Assuming that:

$(K, | ∙ |)$ complete discretely valued field
$characteristic (K) = p > 0$
$k$ is perfect

Then

K = k ((t))

(

k = O_{K} ∕ m

Proof. Since $K = Frac (O_{K})$ , it suffices to show $O_{K} ≅ k [[t]$ . Fix $π \in O_{K}$ a uniformiser, and let $[∙] : k \to O_{K}$ be the Teichmüller map and define

\begin{array}{l} φ : k [[t]] & \to O_{K} \\ φ (\sum_{i = 0}^{\infty} a_{i} t^{i}) & = \sum_{i = 0}^{\infty} [a_{i}] π^{i} \end{array}

Then $φ$ is a ring homomorphism since $[∙]$ is, and it is a bijection by Proposition 3.4(ii). □

6 Extensions of complete valued fields

Theorem 6.1. Assuming that:

$(K, | ∙ |)$ is a complete discretely valued field
$L ∕ K$ a finite extension of degree $n$

Then

(i)

| ∙ |

extends uniquely to an absolute value

{| ∙ |}_{L}

L

defined by

{| y |}_{L} = {| N_{L ∕ L} (y) |}^{\frac{1}{n}} \forall y \in L .

(ii) $L$ is complete with respect to ${| ∙ |}_{L}$ .

Recall: If $L ∕ K$ is finite, $N_{L ∕ K} : L \to K$ is defined by $N_{L ∕ K} (y) = \underset{K}{\det} (m u l t (y)$ where $m u l t (y) : L \to L$ is the $K$ -linear map induced by multiplication by $y$ .

Facts:

$N_{L ∕ K}$ is multiplicative.
Let $X^{n} + a_{n - 1} X^{n - 1} + \dots + a_{0} \in K [X]$ be the minimal polynomial of $y \in L$ . Then $N_{L ∕ K} (y) = \pm a_{0}^{m}$ for some $m \geq 1$ (in fact, $m$ is the degree of $L ∕ K [y]$ ).
$N_{L ∕ K} (y) = 0 ⟺ y = 0$ .

Definition 6.2 (Norm). Let $(K, | ∙ |)$ be a non-archimedean valued field, $V$ a vector space over $K$ . A normon $V$ is a function $∥ ∙ ∥ : V \to ℝ_{\geq 0}$ satisfying:

(i) $∥ x ∥ = 0 ⟺ x = 0$ .
(ii) $∥ λ x ∥ = ∥ λ ∥ ∥ x ∥$ for all $λ \in K$ , $x \in V$ .
(iii) $∥ x + y ∥ \leq \max (∥ x ∥, ∥ y ∥)$ for all $x, y \in V$ .

Example. If $V$ is finite dimensional and $e_{1}, \dots, e_{n}$ is a basis of $V$ . The supremum ${∥ ∙ ∥}_{\sup}$ on $V$ is defined by

{∥ x ∥}_{\sup} = \max_{i} | x_{i} |,

where $x = \sum_{i = 1}^{n} x_{i} e_{i}$ .

Exercise: ${∥ ∙ ∥}_{\sup}$ is a norm.

Definition 6.3 (Equivalent norms). Two norms ${∥ ∙ ∥}_{1}$ and ${∥ ∙ ∥}_{2}$ on $V$ are equivalent if there exists $C, D \in ℝ_{> 0}$ such that

C {∥ x ∥}_{1} \leq {∥ x ∥}_{2} \leq D {∥ x ∥}_{1} \forall x \in V .

Fact: A norm defines a topology on $V$ , and equivalent norms induce the same topology.

Proposition 6.4. Assuming that:

$(K, | ∙ |)$ is a complete non-archimedean valued field
$V$ a finite dimensional vector space over $K$

Then

V

is complete with respect to

{∥ ∙ ∥}_{\sup}

Proof. Let ${(v_{i})}_{i = 1}^{\infty}$ be a Cauchy sequence in $V$ , and let $e_{1}, \dots, e_{n}$ be a basis for $V$ .

Write $v_{i} = \sum_{j = 1}^{n} x_{j}^{i} e_{j}$ . Then ${(x_{j}^{i})}_{i = 1}^{\infty}$ is a Cauchy sequence in $K$ . Let $x_{j}^{i} \to x_{j} \in K$ , then $v_{i} \to v : = \sum_{j = 1}^{n} x_{j} e_{j}$ . □

Theorem 6.5. Assuming that:

$(K, | ∙ |)$ is a complete non-archimedean valued field
$V$ a finite dimensional vector space over $K$

Then any two norms on

K

are equivalent. In particular,

V

is complete with respect to any norm (using Proposition 6.4).

Proof. Since equivalence defines an equivalence relation on the set of norms, it suffices to show that any norm $∥ ∙ ∥$ is equivalent to ${∥ ∙ ∥}_{\sup}$ .

Let $e_{1}, \dots, e_{n}$ be a basis for $V$ , and set $D : = \max_{i} ∥ e_{i} ∥ > 0$ . Then for $x = \sum_{i = 1}^{n} x_{i} e_{i}$ , we have

∥ x ∥ \leq \max_{i} ∥ x_{i} e_{i} ∥ = \max_{i} | x_{i} | ∥ e_{i} ∥ \leq D \max_{i} | x_{i} | = D {∥ x ∥}_{\sup} .

To find $C$ such that $C {∥ ∙ ∥}_{\sup} \leq ∥ ∙ ∥$ , we induct on $n = \dim V$ .

For $n = 1$ : $∥ x ∥ = ∥ x_{1} e_{1} ∥ = | x_{1} | ∥ e_{1} ∥$ , so take $C = ∥ e_{1} ∥$ .

For $n > 1$ : set $V_{i} = span ⟨ e_{1}, \dots, e_{i - 1}, e_{i + 1}, \dots, e_{n} ⟩$ . By induction, $V_{i}$ is complete with respect to $∥ ∙ ∥$ , hence closed.

Then $e_{i} + V_{i}$ is closed for all $i$ , and hence

S : = ⋃_{i = 1}^{n} e_{i} + V_{i}

is a closed subset not containing $0$ . Thus there exists $c > 0$ such that $B (0, C) \cap S = \emptyset$ where $B (0, C) = {x \in V | ∥ x ∥ < C}$ .

Let $0 \neq x = \sum_{i = 1}^{n} x_{i} e_{i}$ and suppose $| x_{j} | = \max_{i} | x_{i} |$ . Then ${∥ x ∥}_{\sup} = | x_{j} |$ , and $\frac{1}{x_{j}} \in S$ . Thus $∥ \frac{x_{i}}{x_{j}} ∥ \geq C$ , and hence

∥ x ∥ \geq C | x_{j} | = C {∥ x ∥}_{\sup} .

$V$ is complete since it is complete with respect to ${∥ ∙ ∥}_{\sup}$ (see Proposition 6.4). □

Definition 6.6 (Integral closure). Let $R$ be a subring of $S$ . We say $s \in S$ is integral over $R$ if there exists a monic polynomial $f (X) \in R [X]$ such that $f (s) = 0$ .

The integral closure $R^{i n t (S)}$ of $R$ inside $S$ is defined to be

R^{i n t (S)} = {s \in S | s integral over R} .

We say $R$ is integrally closed in $S$ if $R^{i n t (S)} = R$ .

Proposition 6.7. $R^{int (S)}$ is a subring of $S$ . Moreover, $R^{int (S)}$ is integrally closed in $S$ .

Proof. Example Sheet 2. □

Lemma 6.8. Assuming that:

$(K, | ∙ |)$ is non-archimedean valued field

Then

O_{K}

is integrally closed in

K

Proof. Let $x \in K$ be integral over $O_{K}$ . Without loss of generality, $x \neq 0$ . Let $f (X) = X^{n} + a_{n - 1} X^{n - 1} + \dots + a_{0} \in O_{K} [X]$ such that $f (x) = 0$ . Then

x = - a_{n - 1} \frac{1}{x} - \dots - a_{0} \frac{1}{x_{n - 1}} .

If $| x | > 1$ , we have $| - a_{n - 1} \frac{1}{x} - \dots - a_{0} \frac{1}{x_{n - 1}} | < 1$ . Thus $| x | \leq 1 ⟹ x \in O_{K}$ . □

Lemma 6.9. $O_{L}$ is the integral closure of $O_{K}$ inside $L$ .

Proof. Let $0 \neq y \in L$ and let

f (X) = X^{d} + a_{d - 1} X^{d - 1} + \dots + a_{0} \in K [X]

be the minimal (monic) polynomial of $y$ .

Claim: $y$ integral over $O_{K}$ if and only if $f (X) \in ℚ_{K} [X]$ .

$\Rightarrow$ Clear.
$\Leftarrow$ Let $g (X) \in O_{K} [X]$ monic such that $g (y) = 0$ . Then $f | g$ (in $K [X]$ ), and hence every root of $f$ is a root of $g$ . So every root of $f$ in $\bar{K}$ is integral over $O_{K}$ , so $a_{i}$ are integral over $O_{K}$ for $i = 0, \dots, d - 1$ .

Hence $a_{i} \in O_{k}$ (by Lemma 6.8). By Corollary 4.5, $| a_{i} | \leq \max (| a_{0} |, 1)$ for $i = 0, \dots, d - 1$ . By property of $N_{L ∕ K}$ , we have $N_{L ∕ K} (y) = \pm a_{0}^{m}$ for $m \geq 1$ .

Hence

\begin{array}{l} y \in O_{L} & ⟺ | N_{L ∕ K} (y) | \leq 1 \\ ⟺ | a_{0} | \leq 1 \\ \overset{C o r o l l a r y 4.5}{⟺} | a_{i} | \leq 1 \forall i, i.e. a_{i} \in O_{K} \end{array}

Thus $O^{K} int (L) = O_{L}$ and proves the Lemma. □

Proof of Theorem 6.1. We first show ${| ∙ |}_{L} = {| N_{L ∕ K} (∙) |}^{\frac{1}{n}}$ satisfies the three axioms in the definition of absolute value.

(i) $\begin{array}{l} {| y |}_{L} = 0 & ⟺ {| N_{L ∕ K} (y) |}^{\frac{1}{n}} = 0 \\ ⟺ N_{L ∕ K} (y) = 0 \\ ⟺ y = 0 \end{array}$
(ii) $\begin{array}{l} {| y_{1} y_{2} |}_{L} & = {| N_{L ∕ K} (y_{1}, y_{2}) |}^{\frac{1}{n}} \\ = {| N_{L ∕ K} (y_{1}) N_{L ∕ K} (y_{2}) |}^{\frac{1}{n}} \\ = {| N_{L ∕ K} (y_{1}) |}^{\frac{1}{n}} {| N_{L ∕ K} (y_{2}) |}^{\frac{1}{n}} \\ = {| y_{1} |}_{L} {| y_{2} |}_{L} \end{array}$
(iii) Set $O_{L} = {y \in L | {| y |}_{L} \leq 1}$ .
Claim: $O_{L}$ is the integral closure of $O_{K}$ inside $L$ .

Assuming this, we prove (iii). Let $x, y \in L$ , and without loss of generality assume ${| x |}_{L} \leq {| y |}_{L}$ . Then ${| \frac{x}{y} |}_{L}$ hence $\frac{x}{y} \in O_{L}$ . Since $1 \in O_{L}$ and $O_{L}$ is a ring, we have $1 + \frac{x}{y} \in O_{L}$ and hence ${| 1 + \frac{x}{y} |}_{L} \leq 1$ . Hence ${| x + y |}_{L} \leq {| y |}_{L} = \max ({| x |}_{L}, {| y |}_{L})$ thus (iii) is satisfied.

So we have proved that $| ∙ |_{L}$ is an absolute value on $L$ .

Since $N_{L ∕ K} (x) = x^{n}$ for $x \in K$ , $| x |_{L}$ extends $| ∙ |$ on $K$ .

If ${| ∙ |}_{L}^{'}$ is another absolute value on $L$ extending $| ∙ |$ , then $| ∙ |_{L}, | ∙ |_{L}^{'}$ are norms on $L$ .

Theorem 6.5 tells us that $| ∙ |_{L}^{'}, | ∙ |_{L}$ induce the same topology on $L$ . Hence $| ∙ |_{L}^{'} = | ∙ |_{L}^{c}$ for some $c > 0$ (by Proposition 1.4) since $| ∙ |_{L}^{'}$ extends $| ∙ |$ , we have $c = 1$ .

Now we show that $L$ is complete with respect to $| ∙ |_{L}$ : this is immediate by Theorem 6.5. □

Let $(K, | ∙ |)$ be a complete discretely valued field.

Corollary 6.10. Let $L ∕ K$ be a finite extension. Then

(i) $L$ is discretely valued with respect to $| ∙ |_{L}$ .
(ii) $O_{L}$ is the integral closure of $O_{K}$ in $L$ .

Proof.

(i) $v$ a valuation on $K$ , $v_{L}$ valuation on $L$ such that $v_{L}$ extends $v$ . Let $n = [L : K]$ , and let $y \in L^{\times}$ . Then $| y |_{L} = | N_{L ∕ K} (y) |^{\frac{1}{n}}$ hence $v_{L} (y) = \frac{1}{n} v (N_{L ∕ K} (y))$ , hence $v_{L} (L^{\times}) \leq \frac{1}{n} v (K^{\times})$ , so $v_{L}$ is discrete.
(ii) Lemma 6.9.

□

Corollary 6.11. Let $\bar{K} ∕ K$ be an algebraic closure of $K$ . Then $| ∙ |$ extends to a unique absolute value $| ∙ |_{\bar{K}}$ on $\bar{K}$ .

Proof. Let $x \in \bar{K}$ , then $x \in L$ for some $L ∕ K$ finite. Define $| x |_{\bar{K}} = | x |_{L}$ . Well-defined, i.e. independent of $L$ by the uniqueness in Theorem 6.1.

The axioms for $| ∙ |_{\bar{K}}$ to be an absolute value can be checked over finite extensions.

Uniqueness: clear. □

Remark. $| ∙ |_{\bar{K}}$ on $\bar{K}$ is never discrete. For example $K = ℚ_{p}$ , $\sqrt[n]{p} \in \bar{ℚ_{p}}$ for all $n \in ℤ_{> 0}$ . Then

v_{p} (\sqrt[n]{p}) = \frac{1}{n} v (p) = \frac{1}{n} .

$\bar{ℚ_{p}}$ is not complete with respect to $| ∙ |_{ℚ_{p}}$ .

Example Sheet 2: $ℂ_{p} : =$ completion of $\bar{ℚ_{p}}$ with respect to $| ∙ |_{\bar{ℚ_{p}}}$ , then $ℂ_{p}$ is algebraically closed.

Proposition 6.12. Assuming that:

$L ∕ K$ finite extension of complete discretely valued fields.
(i): $O_{K}$ is compact.
(ii): The extension of residue fields $k_{L} ∕ k$ is finite and separable.

Then there exists

α \in O_{L}

such that

O_{L} = O_{K} [α]

Later we’ll prove that the (i) implies (ii).

Proof. We’ll choose $α \in O_{L}$ such that:

there exists $β \in O_{L} [α]$ a uniformiser for $O_{L}$
$O_{K} [α] \to k_{L}$ surjective

$k_{L} ∕ k$ separable tells us that there exists $\bar{α} \in k_{L}$ such that $k_{L} = k (\bar{α})$ .

Let $α \in O_{L}$ a lift of $\bar{α}$ , and $g (X) \in O_{K} [X]$ a monic lift of the minimal polynomial of $\bar{α}$ .

Fix $π_{L} \in O_{L}$ a uniformiser. Then $\bar{g} (X) \in k [X]$ irreducible and separable, hence $g (α) \equiv 0 mod π_{L}$ and $g^{'} (α) ⁄ \equiv 0 mod π_{L}$ .

If $g (α) \equiv 0 mod π_{L}^{2}$ , then

g (α + π_{L}) \equiv g (α) + π_{L} g^{'} (α) mod π_{L}^{2} .

Thus

v_{L} (g (α + π_{L})) = v_{L} (π_{L} g^{'} (α)) = v_{L} (π_{L}) = 1 .

( $v_{L}$ normalised valuation on $L$ ).

Thus either $v_{L} (g (α)) = 1$ or $v_{L} (g (α + π_{L})) = 1$ . Upon possibly replacing $α$ by $α + π_{L}$ , we may assume $v_{L} (g (α)) = 1$ .

Set $β = g (α) \in O_{K} [α]$ a uniformiser. Then $O_{K} [α] \subseteq L$ is the image of a continuous map:

\begin{array}{l} O_{K}^{n} & \to L \\ (x_{0}, \dots, x_{n - 1}) & \mapsto \sum_{i = 0}^{n} x_{i} a^{i} \end{array}

where $n = [K (α) : K]$ . Since $O_{K}$ is compact, $O_{K} [α] \subseteq L$ is compact, hence closed. Since $k_{L} = k (\bar{α})$ , $O_{K} [α]$ contians a set of coset representatives for $k_{L} = O_{L} ∕ β O_{L}$ .

Let $y \in O_{L}$ . Then Proposition 3.4 gives us

y = \sum_{i = 0}^{\infty} λ_{i} β^{i}, λ_{i} \in O_{K} [α]

Then $y_{m} = \sum_{i = 0}^{m} λ_{i} β^{i} \in O_{K} [α]$ . Hence $y \in O_{K} [α]$ , since $O_{k} [α]$ is closed. □

Part III
Local Fields

7 Local Fields

Definition 7.1 (Local field). Let $(K, | ∙ |)$ be a valued field. Then $K$ is a local field if it is complete and locally compact.

Reminder: locally compact means for all $x \in K$ , there exists $U$ open and $V$ compact such that $x \in U \subseteq V$ .

Example. $ℝ$ and $ℂ$ are compact.

Proposition 7.2. Assuming that:

$(K, | ∙ |)$ is a non-archimedean complete valued field

Then the following are equivalent:

(i) $K$ is locally compact
(ii) $O_{K}$ is compact
(iii) $v$ is discrete and $k = O_{K} ∕ m$ is finite.

Proof.

(i) $⟹$ (ii) Let $U ∋ 0$ be a compact neighbourhood of $0$ ( $0 \in U \subseteq Z$ with $U$ open, $Z$ compact). Then there exists $x \in O_{K}$ such that $x O_{K} \subseteq U$ . Since $x O_{K}$ is closed, $x O_{K}$ is compact. Hence $O_{K}$ is compact ( $x O_{K} \overset{\cdot x^{- 1}}{\to} O_{K}$ is a homeomorphism).
(ii) $⟹$ (i) $O_{K}$ compact implies $a + O_{K}$ is compact for all $a \in K$ . So $K$ is locally compact.

(ii)

⟹

(iii) Let

x \in m

, and

A_{x} \subseteq O_{K}

be a set of coset representatives for

O_{K} ∕ x O_{K}

. Then

O_{K} = ⋃_{y \in A} y + x O_{K}

is a disjoint open cover. So

A_{x}

is finite by compactness of

O_{K}

. So

O_{K} ∕ x O_{K}

is finite, hence

O_{K} ∕ m O_{K}

is finite.o

Suppose $v$ is not discrete. Then let $x_{1}, x_{2}, \dots$ such that

v (x_{1}) > v (x_{2}) > \dots > 0 .

Then $x O_{K} ⊊ x_{2} O_{K} ⊊ x_{3} O_{K} ⊊ \dots ⊊ O_{K}$ . But $O_{K} ∕ x O_{K}$ is finite so can only have finitely many subgroups, contradiction.

(iii) $⟹$ (ii) Since OK is a metric space, it suffices to prove OK is sequentially compact.
Let ${(x_{n})}_{n = 1}^{\infty}$ be a sequence in $O_{K}$ , and fix $π \in O_{K}$ a uniformiser. Since $π^{i} O_{K} ∕ π^{i + 1} O_{K} ≅ k$ , $O_{K} ∕ π^{i} O_{K}$ is finite for all $i$ ( $O_{K} \supseteq π O_{K} \supseteq \dots \supseteq π^{i} O_{K}$ ). Since $O_{K} ∕ π O_{K}$ is finite, there exists $a_{1} \in O_{K} ∕ π O_{K}$ and a subsequence ${(x_{n})}_{n = 1}^{\infty}$ such that $x_{1 n} \equiv a mod π$ for all $n$ .

Since $O_{K} ∕ π^{2} O_{K}$ is finite, there exists $a_{2} \in O_{K} ∕ π^{2} O_{K}$ and a subsequence ${(x_{2 n})}_{n = 1}^{\infty}$ of ${(x_{1 n})}_{n = 1}^{\infty}$ such that $x_{2 n} \equiv a_{2} {(m o d π)}^{2} O_{K}$ . Continuing, this, we obtain sequences ${(x_{i n})}_{n = 1}^{\infty}$ for $i = 1, 2, \dots$ such that
- (1) ${(x_{(i + 1) n})}_{n = 1}^{\infty}$ is a subsequence of ${(x_{i n})}_{n = 1}^{\infty}$
- (2) For any $i$ , there exists $a_{i} \in O_{K} ∕ π^{i} O_{K}$ such that $x_{i n} \equiv a_{i} mod π^{i}$ for all $n$ .
Then necessarily $a_{i} \equiv a_{i + 1} mod π^{i}$ for all $i$ .

Now choose $y_{i} = x_{i i}$ . This defines a subsequence of ${(x_{n})}_{n = 1}^{\infty}$ . Moreover, $y_{i} \equiv a_{i} \equiv a_{i + 1} \equiv y_{i + 1} mod π^{i}$ . Thus $y_{i}$ is Cauchy, hence converges by completeness. □

Example.

(i) $ℚ_{p}$ is a local field.
(ii) $𝔽_{p} ((t))$ is a local field.

8 Global Fields

Definition 8.1 (Global field). A global field is a field which is either:

(i) An algebraic number field
(ii) A global function field, i.e. a finite extension of $𝔽_{p} (t)$ .

Lemma 8.2. Assuming that:

$(K, | ∙ |)$ is a complete discretely valued field
$L ∕ K$ a finite Galois extension with absolute value ${| ∙ |}_{L}$ extending $| ∙ |$ .

Then for

x \in L

and

σ \in Gal (L ∕ K)

, we have

{| σ (x) |}_{L} = {| x |}_{L}

Proof. Since $x \mapsto {| σ (x) |}_{L}$ is another absolute value on $L$ extending $| ∙ |$ on $K$ , the result follows from uniqueness of ${| ∙ |}_{L}$ . □

Lemma 8.3 (Kummer’s Lemma). Assuming that:

$(K, | ∙ |)$ a complete discretely valued field
$f (X) \in K [X]$ a separable irreducible polynomial with roots $α_{1}, \dots, α_{n} \in K^{sep}$ ( $K^{sep}$ is the separable closure of $K$ )
$β \in K^{sep}$ with
$| β - α_{1} | < | β - α_{i} |$

for $i = 2, \dots, n$ .

Then

α_{1} \in K (β)

Proof. Let $L = K (β)$ , $L^{'} = L (α_{1}, \dots, α_{n})$ . Then $L^{'} ∕ L$ is a Galois extension. Let $σ \in Gal (L^{'} ∕ L)$ . We have

\begin{array}{l} | β - σ (α_{1}) | & = | σ (β - α_{1}) | \\ = | β - α_{1} | \end{array}

using Lemma 8.2. Hence $σ (α_{1}) = α_{1}$ , so $α_{1} \in K (β)$ . □

Proposition 8.4. Assuming that:

$(F, | ∙ |)$ is a complete discretely valued field
$f (X) = \sum_{i = 0}^{n} a_{i} X^{i} \in O_{K} [X]$ a separable irreducible monic polynomial
$α \in K^{sep}$ a root of $f$

Then there exists

𝜀 > 0

such that for any

g (X) = \sum_{i = 0}^{n} b_{i} X^{i} \in O_{K} [X]

monic with

| a_{i} - b_{i} | < 𝜀

for all

i

, there exists a root

β

g (X)

such that

K (α) = K (β)

“Nearby polynomials define the same extensions”.

Proof. Let $α_{1}, \dots, α_{n} \in K^{sep}$ be the roots of $f$ which are necessarily distinct. Then $f^{'} (α_{1}) \neq 0$ . We choose $𝜀$ sufficiently small such that $| g (α_{1}) | < | f^{'} (α_{1}) |^{2}$ and $| f^{'} (α_{1}) - g^{'} (α_{1}) | < | f^{'} (α_{1}) |$ . Then we have $| g^{'} (α_{1}) | < | f^{'} (α_{1}) |^{2} = | g^{'} (α_{1}) |^{2}$ (the equality is by Lemma 1.6).

By Hensel’s Lemma version 1 applied to the field $K (α_{1})$ there exists $β \in K (α_{1})$ such that $g (β) = 0$ and $| ∙ - α_{1} | < | g^{'} (α_{1}) |$ . Then

\begin{array}{l} | g^{'} (α_{1}) | & = | f^{'} (α_{1}) | \\ = \prod_{j = 1}^{n} | α_{1} - α_{j} | \\ \leq | α_{1} - α_{i} | \end{array}

for $i = 2, \dots, n$ . (Use $| α_{1} - α_{i} | \leq 1$ since $α_{i}$ integral). Since $| β - α_{1} | < | α_{1} - α_{i} | = | β - α_{i} |$ using Lemma 1.6, we have that Kummer’s Lemma gives that $α_{1} \in K (β)$ and hence $K (α_{1}) = K (β)$ . □

Theorem 8.5. Assuming that:

$K$ is a local field

Then

K

is the completion of a global field.

Proof. Case 1: $| ∙ |$ is archimedean. Then $ℝ$ is the completion of $ℚ$ , and $ℂ$ is the completion of $ℚ (i)$ (with respect to ${| ∙ |}_{\infty}$ ).

Case 2: $| ∙ |$ non-archimedean, equal characteristic. Then $K ≅ 𝔽_{q} ((t))$ is the completion of $𝔽_{q} (t)$ with respect to the $t$ -adic valuation.

Case 3: $| ∙ |$ non-archimedean mixed characteristic. Then $K = ℚ_{p} (α)$ , with $α$ a root of a monic irreducible polynomial $f (X) \in ℤ_{p} [X]$ . Since $ℤ$ is dense in $ℤ_{p}$ , we choose $g (X) \in ℤ [X]$ as in Proposition 8.4. Then $K = ℚ (β)$ with $β$ a root of $g (X)$ . Since $ℚ (β)$ dense in $ℚ_{p} (β) = K$ , and $K$ is complete, we must have that $K$ is the completion of $ℚ (β)$ . □

Part IV
Dedekind domains

9 Dedekind domains

Definition 9.1 (Dedekind domain). A Dedekind domain is a ring $R$ such that

(i) $R$ is a Noetherian integral domain.
(ii) $R$ is integrally closed in $Frac (R)$ .
(iii) Every non-zero prime ideal is maximal.

Example.

The ring of integers in a number field is a Dedekind domain.
Any PID (hence a discrete valuation ring) is a Dedekind domain.

Theorem 9.2. A ring $R$ is a discrete valuation ring if and only if $R$ is a Dedekind domain with exactly one non-zero prime.

Lemma 9.3. Assuming that:

$R$ is a Noetherian ring
$I \subseteq R$ a non-zero ideal

Then there exists non-zero prime ideals

p_{1}, \dots, p_{r}

such that

p_{1}, \dots, p_{r} \subseteq I

Proof. Suppose not. Since $R$ is Noetherian, we may choose $I$ maximal with this property. Then $I$ is not prime, so there exists $x, y \in R ∖ I$ such that $x, y \in I$ .

Let $I_{1} + (x)$ , $I_{2} = I + (y)$ . Then by maximality of $I$ , there exist $p_{1}, \dots, p_{r}$ and $q_{1}, \dots, q_{s}$ such that $p_{1} \dots p_{r} \subseteq I_{1}$ and $q_{1} \dots q_{s} \subseteq I_{2}$ . Then $p_{1} \dots p_{r} q_{1} \dots q_{s} \subseteq I_{1} I_{2} \subset I$ . □

Lemma 9.4. Assuming that:

$R$ is an integral domain
$R$ is integrally closed in $K = Frac (R)$
$0 \neq I \subseteq R$ a finitely generated ideal
$x \in K$

Then if

x I \subseteq I

, we have

x \in R

Proof. Let $I = (c_{1}, \dots, c_{n})$ . We write

x c_{i} = \sum_{j = 1}^{n} a_{i j} c_{j}

for some $a_{i j} \in R$ . Let $A$ be the matrix $A = {(a_{i j})}_{1 \leq i, j \leq n}$ and set $B = x {id}_{n} - A \in M_{n \times n} (K)$ .

Then in $K^{n}$

B (\begin{matrix} c_{1} \\ ⋮ \\ c_{n} \end{matrix}) = 0 .

Multiply by $adj (B)$ , the adjugate matrix for $B$ . We have

\det (B) {id}_{n} (\begin{matrix} c_{1} \\ ⋮ \\ c_{n} \end{matrix}) = 0 .

Hence $\det (B) = 0$ . But $\det B$ is a monic polynomial with coefficients in $R$ . Then $x$ is integral over $R$ , hence $x \in R$ . □

Proof of Theorem 9.2.

$\Rightarrow$ Clear.
$\Leftarrow$ We need to show $R$ is a PID. The assumption implies that $R$ is a local ring with unique maximal ideal $m$ .
Step 1: $m$ is principal.

Let $0 \neq x \in m$ . By Lemma 9.3, $(x) \supseteq m^{n}$ for some $n \geq 1$ . Let $n$ minimal such that $(x) \supset m^{n}$ , then we may choose $y \in m^{n - 1} ∖ (x)$ .

Set $π = \frac{x}{y}$ . Then we have $y m \subseteq m^{n} \subseteq (x)$ and hence $π^{- 1} m \subseteq R$ . If $π^{- 1} m \subseteq m$ , then $π^{- 1} \in R$ by Lemma 9.4 and $y \in (x)$ , contradiction. Hence $π^{- 1} m = R$ , so $m = π R$ is principal.

Step 2: $R$ is a PID.

Let $I \subseteq R$ be a non-zero ideal. Consider a sequence of fractional ideals $I \subseteq π^{- 1} I \subseteq π^{- 2} I \subseteq \dots$ in $K$ . Then since $π^{- 1} \notin R$ , we have $π^{- k} I \neq π^{- (k + 1)} I$ for all $k$ by Lemma 9.4. Therefore since $R$ is Noetherian, we may choose $n$ maximal such that $π^{- n} I \subseteq R$ . If $π^{- n} I \subseteq m = (π)$ , then $π^{- (n + 1)} \subseteq R$ . So we must have $π^{- n} I = R$ , and hence $I = (π^{n})$ . □

Let $R$ be an integral domain and $S \subseteq R$ a multiplicatively closed subset ( $x, y \in S$ implies $x y \in S$ , and also have $1 \in S$ ). The localisation $S^{- 1} R$ of $R$ with respect to $S$ is the ring

S^{- 1} R = {\frac{r}{s} | r \in R, s \in S} \subseteq Frac (R) .

If $p$ is a prime ideal in $R$ , we write $R_{(p)}$ for the localisation with respect to $S = R ∖ p$ .

Example.

$p = (0)$ , then $R_{(p)} = Frac (R)$ .
$R = ℤ$ , $ℤ_{(p)} = {\frac{a}{b} | a \in ℤ, (b, p) = 1}$ , where $p$ is a rational prime.

Facts: (not proved in this course, but can be found in a typical course / textbook on commutative algebra)

$R$ Noetherian implies $S^{- 1} R$ is Noetherian.

Corollary 9.5. Let $R$ be a Dedekind domain and $p \subseteq R$ a non-zero prime ideal. Then $R_{(p)}$ is a discrete valuation ring.

Proof. By properties of localisation, $R_{(p)}$ is a Noetherian integral domain with a unique non-zero prime ideal $p R_{(p)}$ .

It suffices to show $R_{(p)}$ is integrally closed in $Frac (R_{(p)}) = Frac (R)$ (since then $R_{(p)}$ is a Dedekind domain hence by Theorem 9.2, $R_{(p)}$ is a discrete valuation ring).

Let $x \in Frac (R)$ be integral over $R_{(p)}$ . Multiplying by denominators of a monic polynomial satisfied by $x$ , we obtain

s x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{0} = 0,

with $a_{i} \in R$ , $s \in S = R ∖ p$ . Multiply by $s^{n - 1}$ . Then $x s$ is integral over $R$ , so $x s \in R$ . Hence $x \in R_{(p)}$ . □

Definition 9.6 (Valuation on a Dedekind domain). If $R$ is a Dedekind domain, and $p \subseteq R$ a non-zero prime ideal, we write $v_{p}$ for the normalised valuation on $Frac (R) = Frac (R_{(p)})$ corresponding to the discrete valuation ring $R_{(p)}$ .

Example. $R = ℤ$ , $p = (p)$ , then $v_{p}$ is the $p$ -adiv valuation.

Theorem 9.7. Assuming that:

$R$ is a Dedekind domain
$I \subseteq R$ a non-zero ideal

Then

I

can be written uniquely as aproduct of prime ideals:

I = p_{1}^{e_{1}} \dots p_{r}^{e_{r}}

(with $p_{i}$ distinct).

Remark. Clear for PIDs (PID implies UFD).

Proof (Sketch). We quote the following properties of localisation:

(i) $I = J ⟺ I R_{(p)} = J R_{(p)}$ for all prime ideals $p$ .

(ii) If

R

a Dedekind domain,

p_{1}, p_{2}

non-zero ideals, then

p_{1} R_{(p_{2})} = {\begin{matrix} p_{2} R_{(p_{2})} & p_{1} = p_{2} \\ R_{(p_{2})} & p_{1} \neq p_{2} \end{matrix}

Let $I \subseteq R$ be a non-zero ideal. By Lemma 9.3, there are distinct prime ideals $p_{1}, \dots, p_{r}$ such that $p_{1}^{β_{1}} \dots p_{r}^{β_{r}} \subseteq I$ , where $β_{i} > 0$ .

Let $0 \neq p$ be a prime ideal, $p \notin {p_{1}, \dots, p_{r}}$ . Then property (ii) gives that $p_{i} R_{(p)} = R_{(p)}$ , and hence $I R_{(p)} = R_{(p)}$ .

Corollary 9.5 gives $I R_{(p_{)}} = {(p_{i} R_{(p_{i})})}^{α_{i}} = p_{i}^{α_{i}} R_{(p_{i})}$ for some $0 \leq α_{i} \leq β_{i}$ . Thus $I = p_{1}^{α_{1}} \dots p_{r}^{α_{r}}$ by property (i).

For uniqueness, if $I = p_{1}^{α_{1}} \dots p_{r}^{α_{r}} = p_{1}^{γ_{1}} \dots p_{r}^{γ_{r}}$ then $p_{i}^{α_{i}} R_{(p_{i})} = p_{i}^{γ_{i}} R_{(p_{i})}$ hence $a_{i} = γ_{i}$ by unique factorisation in discrete valuation rings. □

10 Dedekind domains and extensions

Let $L ∕ K$ be a finite extension. For $x \in L$ , we write ${Tr}_{L ∕ K} (x) \in K$ for the trace of the $K$ -linear map $L \to L$ , $y \mapsto x y$ .

If $L ∕ K$ is separable of degree $n$ and $σ_{1}, \dots, σ_{n} : L \to \bar{K}$ denotes the set of embeddings of $L$ into an algebraic closure $\bar{K}$ , then ${Tr}_{L ∕ K} (x) = \sum_{i = 1}^{n} σ_{i} (x) \in K$ .

Lemma 10.1. Assuming that:

$L ∕ K$ a finite separable extension of fields

Then the symmetric bilinear pairing

\begin{array}{l} (∙, ∙) & \to K \\ (x, y) & \mapsto {Tr}_{L ∕ K} (x y) \end{array}

is non-degenerate.

Proof. $L ∕ K$ separable tells us that $L = K (α)$ for some $α \in L$ . Consider the matrix $A$ for $(∙, ∙)$ in the $K$ -basis for $L$ given by $1, α, \dots α^{n - 1}$ .

Then $A_{i j} = {Tr}_{L ∕ K} (α^{i + j}) = {[B B^{⊤}]}_{i j}$ where

B = (\begin{matrix} 1 & 1 & \dots & 1 \\ σ_{1} (α) & σ_{2} (α) & \dots σ_{n} (α) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ σ_{1} (α^{n - 1}) & σ_{2} (α^{n - 1}) & \dots & σ_{n} (α^{n - 1}) \end{matrix})

\det A = \det {(B)}^{2} = {[\prod_{1 \leq i < j \leq n} (σ_{i} (α) - σ_{j} (α))]}^{2}

(Vandermonde determinant), which is non-zero since $σ_{i} (α) \neq σ_{j} (α)$ for $i \neq j$ by separability. □

Exercise: On Example Sheet 3 we will show that a finite extension $L ∕ K$ is separable if and only if the trace form is non-degenerate.

Theorem 10.2. Assuming that:

$O_{K}$ a Dedekind domain
$L$ a finite separable extension of $K = Frac (O_{K})$

Then the integral closure

O_{L}

O_{K}

L

is a Dedekind domain.

Proof. $O_{L}$ a subring of $L$ , hence $O_{L}$ is an integral domain.

Need to show:

(i) $O_{L}$ is Noetherian.
(ii) $O_{L}$ is integrally closed in $L$ .
(iii) Every $\neq 0$ prime ideal $P$ in $O_{L}$ is maximal.

Proofs:

(i) Let $e_{1}, \dots, e_{n} \in L$ be a $K$ -basis for $L$ . Upon scaling by $K$ , we may assume $e_{i} \in O_{L}$ for all $i$ .
Let $f_{i} \in L$ be the dual basis with respect to the trace form $(∙, ∙)$ . Let $x \in O_{L}$ , and write $x = \sum_{i = 1}^{n} λ_{i} f_{i}, λ_{i} \in K$ . Then $λ_{i} = {Tr}_{L ∕ K} (x e_{i}) \in O_{K}$ .

(For any $z \in O_{L}$ , ${Tr}_{L ∕ K} (z)$ is a sum of elements in $\bar{K}$ which are integral over $O_{K}$ . Hence ${Tr}_{L ∕ K} (z) \in K$ is integral over $O_{K}$ , hence ${Tr}_{L ∕ K} (z) \in O_{K}$ .)

Thus $O_{L} \subseteq O_{K} f_{1} + \dots + O_{K} f_{n} \subseteq L$ . Since $O_{K}$ is Noetherian, $O_{L}$ is finitely generated as an $O_{K}$ -module, hence $O_{L}$ is Noetherian.
(ii) Example Sheet 2.

(iii) Let

P

be a non-zero prime ideal of

O_{L}

, and

p : = P \cap O_{K}

be a prime ideal of

O_{K}

. Let

0 \neq x \in P

. Then

x

satisfies an equation

x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{0} = 0, a_{i} \in O_{K},

with $a_{0} \neq 0$ . Then $a_{0} \in P \cap O_{K}$ is a non-zero element of $p$ , hence $p$ is non-zero, hence $p$ is maximal.

We have $O_{K} ∕ p ↪ O_{L} ∕ P$ , and $O_{L} ∕ P$ is a finite dimensional vector space over $O_{K} ∕ p$ . Since $O_{L} ∕ P$ is an integral domain and finite, it is a field. □

Remark. Theorem 10.2 holds without the assumption that $L ∕ K$ is separable.

Corollary 10.3. The ring of integers of a number field is a Dedekind domain.

Convention: $O_{K}$ is the ring of integers of a number field – $p \leq O_{K}$ a non-zero prime ideal. We normalise $| ∙ |_{p}$ (absolute value associated to $v_{p}$ , as defined in Definition 9.6) by $| x |_{p} = {(N p)}^{- v_{p} (x)}$ , where $N_{p} = | O_{K} ∕ p |$ .

In the following theorems and lemmas we will have:

$O_{K}$ a Dedekind domain
$K = Frac (O_{K})$
$L ∕ K$ finite separable
$O_{L}$ the integral closure of $O_{K}$ in $L$ (which is a Dedekind domain by Theorem 10.2).

Lemma 10.4. Assuming that:

$0 \neq x \in O) K$

Then

(x) = \prod_{\begin{array}{c} p \neq 0 \\ prime ideal \end{array}} p^{v_{p} (x)} .

Proof. $x O_{K,_{(p)}} = {(p O_{K, (p)})}^{v_{p} (x)}$ by definition of $v_{p} (x)$ .

Lemma follows from property of localisation

I = J ⟺ I O_{K, (p)} = J O_{K, (p)}

for all prime ideals $p$ . □

Notation. $P \leq O_{L}$ , $p \leq O_{K}$ non-zero prime ideals. We write $P | p$ if $p O_{L} = P_{1}^{e_{1}} \dots P_{r}^{e_{r}}$ and $P \in {P_{1}, \dots, P_{r}}$ ( $e_{i} > 0$ , $P$ distinct).

Theorem 10.5. Assuming that:

$O_{K}$ , $O_{L}$ , $K$ , $L$ as usual
for $p$ a non-zero prime ideal of $O_{K}$ , we write $p O_{L} P_{1}^{e_{1}} \dots P_{r}^{e_{r}}$

Then the absolute values on

L

extending

| ∙ |_{p}

(up to equivalence) are precisely

| ∙ |_{P_{1}}, \dots, | ∙ |_{P_{L}}

Proof. By Lemma 10.4 for any $0 \neq x \in O_{K}$ and $i = 1, \dots, r$ we have $v_{P_{i}} (x) = e_{i} v_{p} (x)$ . Hence, up to equivalence, $| ∙ |_{P_{i}}$ extends $| ∙ |_{p}$ .

Now suppose $| ∙ |$ is an absolute value on $L$ extending $| ∙ |_{p}$ . Then $| ∙ |$ is bounded on $ℤ$ , hence is non-archimedean. Let $R = {x \in L | | x | \leq 1} \leq L$ be the valuation ring for $L$ with respect to $| ∙ |$ . Then $O_{K} \subseteq R$ , and since $R$ is integrally closed in $L$ (Lemma 6.8), we have $O_{L} \subseteq R$ . Set

\begin{array}{l} P & : = {x \in O_{L} | | x | < 1} \\ = m_{R} \cap O_{L} \end{array}

(where $m_{R}$ is the maximal ideal of $R$ ).

Hence $P$ a prime ideal in $O_{L}$ . It is non-zero since $p \subseteq P$ . Then $O_{L, (p)} \subseteq R$ , since $s \in O_{L} ∖ P ⟹ | s | = 1$ .

But $O_{L, (p)}$ is a discrete valuation ring, hence a maximal subring of $L$ , so $O_{L, (p)} = R$ . Hence $| ∙ |$ is equivalent to $| ∙ |_{p}$ . Since $| ∙ |$ extends $| ∙ |_{p}$ , $P \cap O_{K} = p$ so $P_{1}^{e_{1}} \dots P_{r}^{e_{r}} \subseteq P$ , so $P = P_{i}$ for some $i$ . □

Let $K$ be a number field. If $σ : K \to ℝ, ℂ$ is a real or complex embedding, then $x \mapsto | σ (x) |_{\infty}$ defines an absolute value on $K$ (Example Sheet 2) denoted $| ∙ |_{σ}$ .

Corollary 10.6. Let $K$ be a number field with ring of integers $O_{K}$ . Then any absolute value on $K$ is equivalent to either

(i) $| ∙ |_{p}$ for some non-zero prime ideal of $O_{K}$ .
(ii) $| ∙ |_{σ}$ for some $σ : K \to ℝ, ℂ$ .

Proof. Case 1: $| ∙ |$ non-archimedean. Then $| ∙ | |_{ℚ}$ is equivalent to $| ∙ |_{p}$ for some prime $p$ by Ostrowski’s Theorem. Theorem 10.5 gives that $| ∙ |$ is equivalent to $| ∙ |_{p}$ for some $𝔭 \subseteq O_{K}$ a prime ideal with $𝔭 | p$ .

Case 2: $| ∙ |$ archimedean. See Example Sheet 2. □

10.1 Completions

$O_{K}$ a Dedekind domain, $L ∕ K$ a finite separable extension.

Let $𝔭 \subseteq O_{K}$ , $P \subseteq O_{L}$ be non-zero prime ideals with $P | 𝔭$ .

We write $K_{𝔭}$ and $L_{P}$ for the completions of $K$ and $L$ with respect to the absolute values $| ∙ |_{𝔭}$ and $| ∙ |_{P}$ respectively.

Lemma 10.7.

(i) The natural $π_{P} : L \otimes_{K} K_{𝔭} \to L_{P}$ is surjective.
(ii) $[L_{P} : K_{P}] \leq [L : K]$ .

Proof. Let $M = L K_{𝔭} = Im (π_{P}) \subseteq L_{P}$ .

Write $L = K (α)$ then $M = K_{𝔭} (α)$ . Hence $M$ is a finite extension of $K_{𝔭}$ and $[M : K_{𝔭}] \leq [L : K]$ . Moreover $M$ is complete (Theorem 6.1) and since $L \subseteq M \subseteq L_{P}$ , we have $M = L_{P}$ . □

Lemma 10.8 (Chinese remainder theorem). Assuming that:

$R$ a ring
$I_{1}, \dots, I_{n} \subseteq R$ ideals
$I_{i} + I_{j} = R$ for all $i \neq j$

Then

(i) $⋂_{i = 1}^{n} = \prod_{i = 1}^{n} I_{i}$ ( $= I$ say).
(ii) $R ∕ I ≅ \prod_{I = 1}^{n} R ∕ I_{i}$ .

Proof. Example Sheet 2. □

Theorem 10.9. The natural map

L \otimes_{K} K_{𝔭} \to \prod_{P | 𝔭} L_{P}

is an isomorphism.

Proof. Write $L = K (α)$ and let $f (X) \in K [X]$ be the minimal polynomial of $α$ . Then we have

f (X) = f_{1} (X) \dots f_{r} (X) \in K_{𝔭} [X]

where $f_{i} (X) \in K_{𝔭} [X]$ are distinct irreducible (separable). Since $L ≅ K [X] ∕ f (X)$ ,

L \otimes_{K} K_{𝔭} ≅ K_{𝔭} [X] ∕ f_{i} (X) ≅ \prod_{i = 1}^{r} K_{𝔭} [X] ∕ f_{i} (X) .

Set $L_{i} = K_{𝔭} [X] ∕ f_{i} (X)$ a finite extension of $K_{𝔭}$ . Then $L_{i}$ contains both $K_{𝔭}$ and $L$ (use $K [X] ∕ f (x) \to K_{𝔭} [X] ∕ f_{i} (X)$ injective since morphism of fields). Moreover $L$ is dense inside $L_{i}$ (approximate coefficients of $K_{𝔭} [X] ∕ f_{i} (X)$ with an element of $K [X] ∕ f_{i} (X)$ ).

The theorem follows from the following three claims:

(1) $L_{i} ≅ L_{P}$ for some prime $P$ of $O_{L}$ dividing $𝔭$ .
(2) Each $P$ appears at most once.
(3) Each $P$ appears at least once.

Proof of claims:

(1) Since $[L_{i} : K_{𝔭}] < \infty$ , there is a unique absolute value on $L_{i}$ extending $| ∙ |_{𝔭}$ . Theorem 10.5 gives us that $| ∙ | |_{L}$ is equivalent to $| ∙ |_{P}$ for some $P | 𝔭$ . Since $L$ is dense in $L$ and $L_{i}$ is complete, we have $L_{i} ≅ L_{P}$ .
(2) Suppose $φ : L_{i} \to L_{j}$ is an isomorphism preserving $L$ and $K_{𝔭}$ ; then
$φ : K_{𝔭} [X] ∕ f_{i} (X) \to K_{𝔭} [X] ∕ f_{i} (X)$

takes $x$ to $x$ and hence $f_{i} = f_{i}$ .
(3) By Lemma 10.7, the natural map $π_{P} : L \otimes_{K} K_{𝔭} \to L_{P}$ is surjective for any prime $P | 𝔭$ .
Since $L_{P}$ is a field, $π_{P}$ factors through $L_{i}$ for some $i$ , and hence $L_{i} ≅ L_{P}$ by surjectivity of $π_{P}$ . □

Example. $K = ℚ$ , $L = ℚ (i)$ , $f (X) = X^{2} + 1$ . Hensel’s Lemma version 1 gives us that $\sqrt{- 1} \in ℚ_{5}$ . Hence $(5)$ splies in $ℚ (i)$ , i.e. $5 O_{L} = 𝔭_{1} 𝔭_{2}$ .

Corollary 10.10. Let $0 \neq 𝔭 \subseteq O_{K}$ a prime ideal. For $x \in L$ we have

N_{L ∕ K} (x) = \prod_{P | 𝔭} N_{L_{P} ∕ L_{𝔭}} (x) .

Proof. Let $B_{1}, \dots, B_{r}$ be bases for $L_{P_{1}}, \dots, L_{P_{r}}$ as $K_{𝔭}$ -vector spaces. Then $B = ⋃_{i} B_{i}$ is a basis for $L \otimes_{K} K_{𝔭}$ over $K_{𝔭}$ . Let ${[mult (x)]}_{B}$ (respectively ${[mult (x)]}_{B_{i}}$ ) denote the matrix for $mult (x) : L \otimes_{K} K_{𝔭} \to L \otimes_{K} K_{𝔭}$ (respectively $L_{P_{i}} \to L_{P_{i}}$ ) with respect to the basis $B$ (respectively $B_{i}$ ). Then

{[mult (x)]}_{B} = (\begin{matrix} {[mult (x)]}_{B_{1}} \\ ⋱ \\ {[mult (x)]}_{B_{r}} \end{matrix})

hence

\begin{array}{l} N_{L ∕ K} (x) & = \det ({[mult (x)]}_{B}) \\ = \prod_{i = 1}^{r} \det {[mult (x)]}_{B_{i}} \\ = \prod_{i = 1}^{r} N_{L_{P_{i}} ∕ K_{𝔭}} (x) □ \end{array}

11 Decomposition groups

Definition 11.1 (Ramification). Let $0 \neq 𝔭$ be a prime ideal of $O_{K}$ , and

𝔭 O_{L} = P_{1}^{e_{1}} \dots P_{r}^{e_{r}}

with $P_{i}$ distinct prime ideals in $O_{L}$ , and $e_{i} > 0$ .

(i) $e_{i}$ is the ramification index of $P_{i}$ over $𝔭$ .
(ii) We say $𝔭$ ramifies in $L$ if some $e_{i} > 1$ .

Example. $O_{K} = ℂ [t]$ , $O_{L} = ℂ [T]$ . $O_{K} \to O_{L}$ sends $t \mapsto T^{n}$ . Then $t O_{L} = T^{n} O_{L}$ , so the ramification index of $(T)$ over $(t)$ is $n$ .

Corresponds geometrically to the degree $n$ of covering of Riemann surfaces $ℂ \to ℂ$ , $x \mapsto x^{n}$ .

Definition 11.2 (Residue class degree). $f_{i} : = [O_{L} ∕ P_{i} : O_{K} ∕ 𝔭]$ is the residue class degree of $P_{i}$ over $𝔭$ .

Theorem 11.3. $\sum_{i = 1}^{r} e_{i} f_{i} = [L : K]$ .

Proof. Let $S = O_{K} ∖ (𝔭)$ . Exercise (properties of localisation):

(1) $S^{- 1} O_{L}$ is the integral closure of $S^{- 1} O_{K}$ in $L$ .
(2) $S_{- 1} 𝔭 S^{- 1} O_{L} ≅ S^{- 1} P_{1}^{e_{1}} \dots S^{- 1} P_{r}^{e_{r}}$ .
(3) $S^{- 1} O_{L} ∕ S^{- 1} P_{i} ≅ O_{L} ∕ P_{i}$ and $S^{- 1} O_{K} ∕ S^{- 1} 𝔭 ≅ O_{K} ∕ 𝔭$ .

In particular, (2) and (3) imply $e_{i}$ and $f_{i}$ don’t change when we replace $O_{K}$ and $O_{L}$ by $S^{- 1} O_{K}$ and $S^{- 1} O_{L}$ .

Thus we may assume that $O_{K}$ is a discrete valuation ring (hence a PID). By Chinese remainder theorem, we have

O_{L} ∕ 𝔭 O_{L} ≅ \prod_{i = 1}^{r} O_{L} ∕ P_{i}^{e_{i}} .

We count dimension as $k : = O_{K} ∕ 𝔭$ vector spaces.

RHS: for each $i$ , there exists a decreasing sequence of $k$ -suibspaces

0 \subseteq P_{i}^{e_{i} - 1} ∕ P_{i}^{e_{i}} \subseteq \dots \subseteq P_{i} ∕ P_{i}^{e_{i}} \subseteq O_{L} ∕ P_{i}^{e_{i}} .

Thus $\dim_{k} O_{L} ∕ P_{i}^{e_{i}} = \sum_{j = 0}^{e_{i} - 1} \dim_{k} (P_{i}^{j} ∕ P_{i}^{j + 1})$ . Note that $P_{i}^{j} ∕ P_{i}^{j + 1}$ is an $O_{L} ∕ P_{i}$ -module and $x \in P_{i}^{j} ∖ P_{i}^{j + 1}$ is a generator (for example can prove this after localisation at $P_{i}$ ).

Then $\dim_{k} P_{i}^{j} ∕ P_{i}^{j + 1} = f_{i}$ and we have

\dim_{k} O_{L} ∕ P_{i}^{e_{i}} = e_{i} f_{i},

and hence

\dim_{k} \prod_{i = 1}^{r} O_{L} ∕ P_{i}^{e_{i}} = \sum_{i = 1}^{r} e_{i} f_{i} .

LHS: Structure theorem for finitely generated modules over PIDs tells us that $O_{L}$ is a free module over $O_{K}$ of rank $n$ .

Thus $O_{L} ∕ 𝔭 O_{L} ≅ {(O_{K} ∕ 𝔭)}^{n}$ as $k$ -vector spaces, hence $\dim_{k} O_{L} ∕ 𝔭 O_{L} = n$ . □

Geometric analogue:

$f : X \to Y$ a degree $n$ cover of compact Riemann surfaces. For $y \in Y$ :

n = \sum_{x \in f^{- 1} (y)} e - x

where $e_{x}$ is the ramification index of $x$ . Now assume $L ∕ K$ is Galois. Then for any $σ \in Gal (L ∕ K)$ , $σ (P_{i}) \cap O_{K} = 𝔭$ and hence $σ (P_{i}) \in {P_{1}, \dots, P_{r}}$ .

Proposition 11.4. The action of $Gal (L ∕ K)$ on ${P_{1}, \dots, P_{r}}$ is transitive.

Proof. Suppose not, so that there exists $i \neq j$ such that $σ (P_{i}) \neq P_{j}$ for all $σ \in Gal (L ∕ K)$ .

By Chinese remainder theorem, we may choose $x \in O_{L}$ such that $x \equiv 0 m o d P_{i}$ , $x \equiv 1 m o d σ (P_{i})$ for all $σ \in Gal (L ∕ K)$ . Then

N_{L ∕ K} (x) = \prod_{σ \in Gal (L ∕ K)} σ (x) \in O_{K} \cap P_{i} = 𝔭 \subseteq P_{j} .

Since $P_{j}$ prime, there exists $τ \in Gal (L ∕ K)$ such that $τ (x) \in P_{j}$ . Hence $x \in τ^{- 1} (P_{j})$ , i.e. $x \equiv 0 m o d τ^{- 1} (P_{j})$ , contradiction. □

Corollary 11.5. Suppose $L ∕ K$ is Galois. Then $e_{1} = \dots = e_{r} = e$ , $f_{1} = \dots = f_{r} = f$ , and we have $n = e f r$ .

Proof. For any $σ \in Gal (L ∕ K)$ we have

(i) $𝔭 O_{L} = σ (𝔭) O_{L} = σ {(P_{1})}^{e_{1}} \dots σ {(P_{r})}^{e_{r}}$ , hence $e_{1} = \dots = e_{r}$ .
(ii) $O_{L} ∕ P_{i} ≅ O_{L} ∕ σ (P_{i})$ via $σ$ . Hence $f_{1} = \dots = f_{r}$ . □

If $L ∕ K$ is an extension of complete discretely valued fields with normalised valuations $v_{L}$ , $v_{K}$ and uniformisers $π_{L}, π_{K}$ , then the ramification index is $e = e_{L ∕ K} = v_{L} (π_{K})$ . The residue class degree is $f : = f_{L ∕ K} = [k_{L} : k]$ .

Corollary 11.6. Let $L ∕ K$ be a finite separable extension. Then $[L : K] = e f$ .

$O_{K}$ a Dedekind domain:

Definition 11.7 (Decomposition). Let $L ∕ K$ be a finite Galois extension. The decomposition at a prime $P$ of $O_{L}$ is the subgroup of $Gal (L ∕ K)$ defined by

G_{P} = {σ \in Gal (L ∕ K) | σ (P) = P} .

Proposition 11.8. Assuming that:

$O_{K}$ a Dedekind domain
$L ∕ K$ a finite Galois extension
$0 \neq P \subseteq O_{L}$ a prime ideal
$P | 𝔭 \subseteq O_{K}$

Then

(i) $L_{P} ∕ K_{𝔭}$ is Galois.
(ii) There is a natural map
$res : Gal (L_{P} ∕ K_{𝔭}) \to Gal (L ∕ K)$

which is injective and has image $G_{P}$ .

Proof.

(i) $L ∕ K$ Galois implies that $L$ is a splitting field of a separable polynomial $f (X) \in K [X]$ . Hence $L_{P}$ is the splitting field of $f (X) \in K_{[} X]$ , hence $L_{P} ∕ K_{𝔭}$ is Galois.
(ii) Let σ ∈ Gal ⁡ (LP∕K𝔭), then σ(L) = L since L∕K is normal, hence we have a map res ⁡ : Gal ⁡ (LP∕K𝔭) → Gal ⁡ (L∕K), σ↦σ|L. Since L is dense in LP, res ⁡ is injective. By Lemma 8.2, we have
$| σ (x) |_{P} = | x |_{P}$

for all $σ \in Gal (L_{P} ∕ K_{𝔭})$ and $x \in L_{P}$ . Hence $σ (P) = P$ for all $σ \in Gal (L_{P} ∕ K_{𝔭})$ and hence $res (σ) \in G_{P}$ for all $σ \in Gal (L_{P} ∕ K_{𝔭})$ .

To show surjectivity, it suffices to show that
$| G_{P} | = e f = [L_{P} : K_{𝔭}] .$

Write $𝔭 O_{L} = P_{1}^{e_{1}} \dots P_{r}^{e_{r}}$ , $f = [O_{L} ∕ P : O_{K} ∕ 𝔭]$ . Then
- $| G_{P} | = \frac{| Gal (L ∕ K) |}{r} = \frac{e f r}{r} = e f$ (using Corollary 11.5).
- $[L_{P} : K_{𝔭}] = e f$ . Apply Corollary 11.6 to $L_{P} ∕ K_{𝔭}$ , noting that $e, f$ don’t change when we take completions. □

Part V
Ramification Theory

$p = 𝔭_{1} 𝔭_{2}$ in $ℤ [i]$ if and only if $p = x^{2} + y^{2}$ .

We will consider $L ∕ K$ extension of algebraic number fields with $[L : K] = n$ .

12 Different and discriminant

Notation. Let $x_{1}, \dots, x_{n} \in L$ . Set

\begin{array}{l} Δ (x_{1}, \dots, x_{n}) & = \det ({Tr}_{L ∕ K} (x_{i} x_{j})) \in K \\ = \det (\sum_{k = 1}^{n} σ_{k} (x_{i}) σ_{k} (x_{j})) \\ = \det (B B^{⊤}) \end{array}

where $σ_{k} : L \to \bar{K}$ are distinct embeddings and $B = (σ_{i} (x_{j}))$ .

Note:

If $y_{i} = \sum_{j = 1}^{n} a_{i j} x_{j}$ , $a_{i j} \in K$ , then
$Δ (y_{1}, \dots, y_{n}) = \det {(A)}^{2} Δ (x_{1}, \dots, x_{n})$

where $A = (a_{i j})$ .
If $x_{1}, \dots, x_{n} \in O_{L}$ , then $Δ (x_{1}, \dots, x_{n}) \in O_{K}$ .

Lemma 12.1. Assuming that:

$k$ a perfect field
$R$ a $k$ -algebra which is finite dimensional as a $k$ -vector space

Then the Trace form

\begin{array}{l} (∙, ∙) : R \times R & \to R \\ (x, y) & \mapsto {Tr}_{R ∕ k} (x y) (: = {Tr}_{k} (mult (x y))) \end{array}

is non-degenerate if and only if $R = k_{1} \times \dots \times k_{r}$ where $k_{i} ∕ k$ is a finite separable extension of $k$ .

Proof. Example Sheet 3. □

Theorem 12.2. Assuming that:

$0 \neq 𝔭 \subseteq O_{K}$ prime ideal

Then

(i) If $𝔭$ ramifies in $L$ , then for every $x_{1}, \dots, x_{n} \in O_{L}$ , we have $Δ (x_{1}, \dots, x_{n}) \equiv 0 mod 𝔭$ .
(ii) If $𝔭$ is unramified in $L$ , then there exists $x_{1}, \dots, x_{n}$ such that $𝔭 ∤ (Δ (x_{1}, \dots, x_{n}))$ .

Proof.

(i) Let

𝔭 O_{L} = P_{1}^{e_{1}} \dots P_{r}^{e_{r}}

0 \neq P_{i} \subseteq O_{L}

distinct prime ideals,

e_{i} > 0

. Define

R : = O_{L} ∕ 𝔭 O_{L} \overset{CRT}{=} \prod_{i = 1}^{r} O_{L} ∕ P_{i}^{e_{i}} .

If $𝔭$ ramifies, then $O_{L} ∕ 𝔭 O_{L}$ has nilpotents. Hence

Δ ({\bar{x}}_{1}, \dots, {\bar{x}}_{n}) = 0 \forall {\bar{x}}_{i} \in O_{L} ∕ 𝔭 O_{L} .

Then using the fact that

𝒪 R = 𝒪 ∕𝔭𝒪
L L L

TrTrLR𝒪∕∕KKk k = 𝒪K ∕𝔭

commutes, we get that

Δ (x_{1}, \dots, x_{n}) \equiv 0 mod 𝔭 \forall x_{i} \in O_{L} ∕ 𝔭 O_{L} .

(ii) $𝔭$ unramified implies $R = O_{L} ∕ 𝔭 O_{L}$ is a product of finite extensions of $k$ . By Lemma 12.1, we get that the Trace form is non-degenerate, hence for ${\bar{x}}_{1}, \dots, {\bar{x}}_{n}$ a basis of $O_{L} ∕ 𝔭 O_{L}$ as a $k$ vector space, we have $Δ ({\bar{x}}_{1}, \dots, {\bar{x}}_{n}) \neq 0$ . So thee exist $x_{1}, \dots, x_{n} \in O_{L}$ such that
$Δ (x_{1}, \dots, x_{n}) ⁄ \equiv 0 mod 𝔭 . □$

Definition 12.3 (Discriminant). The discriminant is the ideal $d_{L ∕ K} \subseteq O_{K}$ generated by $Δ (x_{1}, \dots, x_{n})$ for all choices of $x_{1}, \dots, x_{n} \in O_{L}$ .

Corollary 12.4. $𝔭$ ramifies $L$ if and only if $𝔭 | d_{L ∕ K}$ . In particular, only finitely many primes ramify in $L$ .

Definition 12.5 (Inverse different). The inverse different is

D_{L ∕ K}^{- 1} = {y \in L : {Tr}_{L ∕ K} (x y) \in O_{K} \forall x \in O_{L}},

an $O_{L}$ submodule of $L$ .

Lemma 12.6. $D_{L ∕ K}^{- 1}$ is a fractional ideal in $L$ .

Proof. Let $x_{1}, \dots, x_{n} \in O_{L}$ a $K$ -basis for $L ∕ K$ . Set

d : = Δ (x_{1}, \dots, x_{n}) = \det ({Tr}_{L ∕ K} (x_{i} x_{j})),

which is non-zero since separable.

For $x \in D_{L ∕ K}^{- 1}$ write $x = \sum_{j = 1}^{r} λ_{j} x_{j}$ with $λ_{j} \in K$ . We show $λ_{j} \in \frac{1}{d} O_{K}$ . We have

{Tr}_{L ∕ K} (x x_{i}) = \sum_{j = 1}^{n} λ_{j} {Tr}_{L ∕ K} (x_{i} x_{j}) \in O_{K} .

Set $A_{i j} = {Tr}_{L ∕ K} (x_{i} x_{j})$ . Multiplying by $Adj (A) \in M_{n} (O_{K})$ , we get

d (\begin{matrix} λ_{1} \\ ⋮ \\ λ_{n} \end{matrix}) = Adj (A) (\begin{matrix} {Tr}_{L ∕ K} (x x_{1}) \\ ⋮ \\ {Tr}_{L ∕ K} (x x_{n}) \end{matrix})

Since $λ_{i} \in \frac{1}{d} O_{K}$ , we have $x \in \frac{1}{d} O_{L}$ . Thus $D_{L ∕ K}^{- 1} \leq \frac{1}{d O_{K}}$ , so $D_{L ∕ K}^{- 1}$ is a fractional ideal. □

The inverse $D_{L ∕ K}$ of $D_{L ∕ K}^{- 1}$ is the different ideal.

Remark. $D_{L ∕ K} \leq O_{L}$ since $O_{L} \subseteq D_{L ∕ K}^{- 1}$ .

Let $I_{L}$ , $I_{K}$ be the groups of fractional ideals.

Theorem 9.7 gives that

I_{L} ≅ \underset{\begin{array}{c} 0 \neq P \\ prime ideals in O_{L} \end{array}}{\otimes} ℤ, I_{K} ≅ \underset{\begin{array}{c} 0 \neq P \\ prime ideals in O_{K} \end{array}}{\otimes} .

Define $N_{L ∕ K} : I_{L} \to I_{K}$ induced by $P \mapsto 𝔭^{f}$ for $𝔭 = P \cap O_{K}$ and $f = f (P ∕ 𝔭)$ .

Fact:

(Use Corollary 10.10 and

v_{𝔭} (N_{L_{P} ∕ K_{𝔭}} (x)) = f_{P ∕ 𝔭} v_{(} x)

for

x \in L^{P} \times

where

v_{𝔭}

and

v_{P}

are the normalised valuations for

L_{P}

K_{𝔭}

Theorem 12.7. $N_{L ∕ K} (D_{L ∕ K}) = d_{L ∕ K}$ .

Proof. First assume $O_{K}$ , $O_{L}$ are PIDs. Let $x_{1}, \dots, x_{n}$ be an $O_{K}$ -basis for $O_{L}$ and $y_{1}, \dots, y_{n}$ be the dual basis with respect to trace form. Then $y_{1}, \dots, y_{n}$ is a basis for $D_{L ∕ K}^{- 1}$ . Let $σ_{1}, \dots, σ_{n} : L \to \bar{K}$ be the distinct embeddings. Have

\sum_{i = 1}^{n} σ_{i} (x_{j}) σ_{i} (y_{k}) = Tr (x_{j} y_{k}) = δ_{j k} .

But

Δ (x_{1}, \dots, x_{n}) = \det {(σ_{i} (x_{j}))}^{2} .

Thus

Δ (x_{1}, \dots, x_{n}) Δ (y_{1}, \dots, y_{n}) = 1 .

Write $D_{L ∕ K}^{- 1} = β O_{L}$ since $β \in L$ . Then

\begin{array}{l} d_{L ∕ K}^{- 1} & = (Δ {(x_{1}, \dots, x_{n})}^{- 1}) \\ = (Δ (y_{1}, \dots, y_{n})) \\ = (Δ (β x_{1}, \dots, β x_{n})) & change of basis matrix is invertible in O_{K} \\ = N_{L ∕ K} (β^{2}) Δ (x_{1}, \dots, x_{n}) & change of basis matrix is [mult (β)] \end{array}

Thus

d_{L ∕ K}^{- 1} = N_{L ∕ K} {(D_{L ∕ K}^{- 1})}^{2} d_{L ∕ K}

N_{L ∕ K} (D_{L ∕ K}) = d_{L ∕ K} .

In general, localise at $S = O_{K} ∖ 𝔭$ and use $S^{- 1} D_{L ∕ K} = D_{S^{- 1}} O_{L} ∕ S^{- 1} O_{K}$ . Then $S^{- 1} d_{L ∕ K} = d_{S^{- 1} O_{L} ∕ S^{- 1} O_{K}}$ . Details omitted. □

Theorem 12.8. Assuming that:

$O_{L} = O_{K} [α]$
$α$ has monic minimal polynomial $g (X) \in O_{K} [X]$

Then

D_{L ∕ K} = (g^{'} (α))

Proof. Let $α = α_{1}, \dots, α_{n}$ be the roots of $g$ . Write

\frac{g (X)}{X - α} = β_{n - 1} X^{n - 1} + \dots + β_{1} X + β_{0}

with $β_{i} \in O_{L}$ and $β_{n - 1} = 1$ . We claim

\sum_{i = 1}^{n} \frac{g (X)}{X - α_{i}} \frac{α_{i}^{n}}{g^{'} (α_{i})} = X^{r}

for $0 \leq r \leq n - 1$ .

Indeed the difference is a palynomial of degree $< n$ , which vanishes for $X = α_{1}, \dots, α_{n}$ . Equate coefficients of $X^{s}$ , which gives

{Tr}_{L ∕ K} (\frac{α^{r} β_{s}}{g^{'} (α)}) = δ_{r s} .

Since $1, α, \dots, α^{n - 1}$ is an $O_{K}$ basis for $O_{L}$ , $D_{L ∕ K}^{- 1}$ has an $O_{K}$ basis

\frac{β_{0}}{g^{'} (α)}, \frac{β_{1}}{g^{'} (α)}, \dots, \underset{\frac{1}{g^{'} (α)}}{\underset{⏟}{\frac{β_{n - 1}}{g^{'} (α)}}} .

Note all of these are $O_{L}$ multiples of the last term, since the $β_{i}$ are in $O_{L}$ . So $D_{L ∕ K}^{- 1} = \frac{1}{(g^{'} (α))}$ , hence $D_{L ∕ K} = (g^{'} (α))$ . □

$P$ a prime ideal of $O_{L}$ , $𝔭 = O_{K} \cap P$ . $D_{L_{P}} ∕ K_{𝔭}$ using $O_{K_{𝔭}}$ , $O_{L_{P}}$ . We identify $D_{L_{P}} ∕ K_{𝔭}$ with a power $P$ .

Theorem 12.9. $D_{L ∕ K} = \prod_{P} D_{L_{P}} ∕ K_{𝔭}$ (finite product, see later).

Proof. Let $x \in L$ , $𝔭 \subseteq O_{K}$ . Then

Tr L ∕ K (x) = \sum_{P | 𝔭} {Tr}_{L_{P} ∕ K_{𝔭}} (x) (∗)

(of Corollary 10.10).

Let $r (P) = v_{P} (D_{L ∕ K})$ , $s (P) = v_{P} (D_{L_{P}} ∕ K_{𝔭})$ .

$\subseteq$ (i.e. $r (P) \geq s (P)$ ). Let $x \in L$ with $v_{P} (x) \geq - s (P)$ for all $P$ . Then ${Tr}_{L_{P} ∕ K_{𝔭}} (x y) \in O_{K_{𝔭}}$ , for all $y \in L$ and for all $P$ . Using ( $*$ ) we get
${Tr}_{L ∕ K} (x y) \in O_{K_{𝔭}} \forall y \in O_{L}, \forall P .$

Thus
${Tr}_{L ∕ K} (x y) \in O_{K} \forall y \in O_{L}$

so $D_{L ∕ K} \subseteq \prod_{P} D_{L_{P}} ∕ K_{𝔭}$ .

\supseteq

(i.e.

r (P) \leq s (P)

). Fix

P

and let

x \in P^{- r (P)} ∖ P^{- r (P) + 1}

. Then

v_{P} (x) = - r (P)

v_{P^{'}} (x) \geq 0

for all

P^{'} \neq P

. By (

*

) , we have

{Tr}_{L_{P} ∕ K_{𝔭}} (x y) = {Tr}_{L ∕ K} (x y) - \sum_{\begin{array}{c} P^{'} | 𝔭 \\ P^{'} \neq P \end{array}} {Tr}_{L_{P} ∕ K_{𝔭}} (x y) \forall y \in O_{L}

hence

{Tr}_{L_{P} ∕ K_{𝔭}} (x y) \in O_{K_{𝔭}} \forall y \in O_{L_{P}} .

Hence $x \in D_{L_{P}} ∕ K_{𝔭} - 1$ , i.e. $- v_{P} (x) = r (P) \leq s (P)$ . So $D_{L ∕ K} \supseteq \prod_{P} D_{L_{P}} ∕ K_{𝔭}$ . □

Corollary 12.10. $d_{L ∕ K} = \prod_{P | 𝔭} d_{L_{P} ∕ K_{𝔭}}$ .

Proof. Apply $N_{L ∕ K}$ to $D_{L ∕ K} = \prod_{P | 𝔭} D_{L_{P}} ∕ K_{𝔭}$ . □

13 Unramified and totally ramified extensions of local fields

Let $L ∕ K$ be a finite separable extension of non-archimedean local fields. Corollary 11.6 implies

[L : K] = e_{L ∕ K} f_{L ∕ K} . (∗)

Lemma 13.1. Assuming that:

$M ∕ L ∕ K$ finite separable extensions of local fields

Then

(i) $f_{M ∕ K} = f_{L ∕ K} f_{M ∕ L}$
(ii) $e_{M ∕ K} = e_{L ∕ K} f_{M ∕ L}$

Proof.

(i) $f_{M ∕ K} = [k_{M} : k] = [k_{M} : k_{L}] [k_{L} : k] = f_{M ∕ L} f_{L ∕ K}$ .
(ii) (i) and ( $*$ ). □

Definition 13.2 (Unramified / ramified / totally ramified). The extension $L ∕ K$ is said to be:

unramified if $e_{L ∕ K} = 1$ (equivalently $f_{L ∕ K} = [L : K]$ ).
ramified if $e_{L ∕ K} > 1$ (equivalently $f_{L ∕ K} < [L : K]$ ).
totally ramified if $e_{L ∕ K} = [L : K]$ (equivalently $f_{L ∕ K} = 1$ ).

From now on in this course: if unspecified $L ∕ K$ is a finite separable extension of (non-archimedean) local fields. Also, all local fields that we consider from now on will be non-archimedean.

Theorem 13.3. Assuming that:

$L ∕ K$ a finite separable extension of non-archimedean local fields

Then there exists a field

K_{0}

K \subseteq K_{0} \subseteq L

and such that

(i) $K_{0}$ is unramified
(ii) $L ∕ K_{0}$ is totally ramified

Moreover $[L : K_{0}] = e_{L ∕ K}$ , $[K_{0} : K] = f_{L ∕ K}$ and $K_{0} ∕ K$ is Galois.

Proof. Let $k = 𝔽_{q}$ , so that $k_{L} = 𝔽_{q^{f}}$ , $f_{L ∕ K} = f$ . Set $m = q^{f} - 1$ , $[∙] : 𝔽_{q^{f}} \to L$ the Teichmüller map for $L$ .

Let $ζ_{m} : = [α]$ for $α$ a generator of $𝔽_{q^{f}}^{\times}$ . $ζ_{m}$ a primitive $m$ -th root of unity. Set $K_{0} = K (ζ_{m}) \subseteq L$ , then $K_{0} ∕ K$ is Galois and has residue field $k_{0} = 𝔽_{q} (α) = k_{L}$ . Hence $f_{L ∕ K_{0}} = 1$ , i.e. $L ∕ K_{0}$ is totally ramified.

Let $res : Gal (K_{0} ∕ K) \to Gal (k_{0} ∕ k)$ be the natural map. For $σ \in Gal (K_{0} ∕ K)$ . We have $σ (ζ_{m}) = ζ_{m}$ if $σ (ζ_{m}) \equiv ζ_{m} mod m$ (since $μ_{m} (K_{0}) ≅ μ_{m} (k_{0})$ by Hensel’s Lemma version 1). Hence $res$ is injective. Thus $| Gal (K_{0} ∕ K) | \leq | Gal (k_{0} ∕ k) | = f_{K_{0} ∕ K}$ , so $[K_{0} : K] = f_{K_{0} ∕ K}$ .

Hence $res$ is an isomorphism, and $K_{0} ∕ K$ is unramified. □

Theorem 13.4. Assuming that:

$k = 𝔽_{q}$
$n \geq 1$

Then there exists a unique unramified

L ∕ K

of degree

n

. Moreover,

L ∕ K

is Galois and the natural

Gal (L ∕ K) \to Gal (k_{L} ∕ k)

is an isomorphism. In particular,

Gal (L ∕ K) ≅ ⟨ {Frob}_{L ∕ K} ⟩

is cyclic, where

{Frob}_{L ∕ K} (x) = x^{q} mod m_{L}

for all

x \in O_{L}

Proof. For $n \geq 1$ , take $L = K (ζ_{m})$ where $m = q^{n} - 1$ .

As in Theorem 13.3:

Gal (L ∕ K) \tilde{\to} Gal (k_{L} ∕ K) ≅ Gal (𝔽_{q^{n}} ∕ 𝔽_{q}) .

Hence $Gal (L ∕ K)$ is cyclic, generated by a lift of $x \mapsto x^{q}$ .

Uniqueness: $L ∕ K$ of degree $n$ unramified. Then Teichmüller gives $ζ_{m} \in L$ , so $L = K (ζ_{m})$ . □

Corollary 13.5. $L ∕ K$ a finite Galois extension. Then $res : Gal (L ∕ K) \to Gal (k_{L} ∕ k)$ is surjective.

Proof. $res$ factorises as

Gal (L ∕ K) ↠ Gal (K_{0} ∕ K) \tilde{\to} Gal (k_{L} ∕ k) . □

Definition 13.6 (Inertial subgroup). The inertial subgroup is

I_{L ∕ K} = \ker (Gal (L ∕ K) ↠ Gal (k_{L} ∕ k)) .

Since $e_{L ∕ K} f_{L ∕ K} = [L : K]$ , we have $| I_{L ∕ K} | = e_{L ∕ K}$ .
$I_{L ∕ K} = Gal (L ∕ K_{0})$ – $K_{0}$ as in Theorem 13.3.

Definition 13.7 (Eisenstein polynomial). $f (x) = x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{0} \in O_{K} [x]$ is Eisenstein if $v_{K} (a_{i}) \geq 1$ for all $i$ , and $v_{K} (a_{0}) = 1$ .

Fact: $f (x)$ Eisenstein implies $f (x)$ irreducible.

Theorem 13.8.

(i) Let $L ∕ K$ finite totally ramified, $π_{L} \in O_{L}$ a uniformiser. Then the minimal polynomial of $π_{L}$ is Eisenstein and $O_{L} = O_{K} [π_{L}]$ (hence $L = K (π_{L})$ )
(ii) Conversely, if $f (x) \in O_{K} [x]$ is Eisenstein and a root of if f, then $L : = K (α) ∕ K$ is totally ramified and $α$ is a uniformiser of $L$ .

Proof.

(i)

[L : K] = e = e_{L ∕ K}

. Let

f (x) = x^{m} + a_{m - 1} x^{m - 1} + \dots + a_{0} \in O_{K} [x]

the minimal polynomial for $π_{L}$ . Then $m \leq e$ . Since $v_{L} (K^{\times}) = e ℤ$ , we have $v_{L} (a_{i} π^{i}) \equiv e mod e$ , for $i < m$ . Hence these terms have distinct valuations. As

π_{L}^{m} = - \sum_{i = 0}^{m - 1} a_{i} π_{L}^{i} .

we have

m = v_{L} (π_{L}^{m}) = \min_{0 \leq i \leq m - 1} (i + e v_{K} (a_{i}))

hence $v_{K} (a_{i}) \geq 1$ for all $i$ .

Hence $v_{K} (a_{0}) = 1$ and $m = e$ . Thus $f (x)$ is Eisenstein and $L = K (π_{L})$ . For $y \in L$ , we write $y = \sum_{i = 0}^{e - 1} π_{L}^{i} b_{i}$ , $b_{i} \in K$ . Then

v_{L} (y) = \min_{0 \leq i \leq e - 1} (i + e v_{K} (b_{i})) .

Thus

\begin{array}{l} y \in O_{L} & ⟺ v_{L} (y) \geq 0 \\ ⟺ v_{K} (b_{i}) \geq 0 \forall i \\ ⟺ y \in O_{K} [π_{L}] \end{array}

(ii) Let $f (x) = x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{0}$ is Eisenstein and $e = e_{L ∕ K}$ . Thus $v_{L} (a_{i}) \geq e$ and $v_{L} (a_{0}) = e$ . If $v_{L} (α) \leq 0$ , we have
$v_{L} (α^{n}) < v_{L} (\sum_{i = 0}^{n - 1} a_{i} α^{i})$

hence $v_{L} (α) > 0$ . For $i \neq 0$ , $v_{L} (a_{i} α^{i}) > e = v_{L} (a_{0})$ . Therefore
$v_{L} (α^{n}) = v_{L} (- \sum_{i = 0}^{n - 1} a_{i} α^{i}) = v_{L} (a_{0}) = e .$

Hence $n v_{L} (α) = e$ . But $n = [L : K] \geq e$ , so $n = e$ and $v_{L} (α) = 1$ .

□

13.1 Structure of Units

Let $[K : ℚ] < \infty$ , $e : = e_{K ∕ ℚ_{p}}$ , $π$ a uniformiser in $K$ .

Proposition 13.9. Assuming that:

$r > \frac{e}{p - 1}$

Then

\exp (x) = \sum_{n = 0}^{\infty} \frac{x^{n}}{n!}

converges on

π^{r} O_{K}

and induces an isomorphism

(π^{r} O_{K}, +) \tilde{\to} (1 + π^{r} O_{K}, \times) .

Proof.

\begin{array}{l} v_{K} (n!) & = e v_{p} (n!) \\ = \frac{e (n - s_{p} (n))}{p - 1} & Example Sheet 1 \\ \leq e (\frac{n - 1}{p - 1}) \end{array}

For $x \in π^{r} O_{K}$ and $n \geq 1$ ,

\begin{array}{l} v_{K} (\frac{x^{n}}{n!}) & \geq n r - \frac{e (n - 1)}{p - 1} \\ = r - (n - 1) \underset{> 0}{\underset{⏟}{(r - \frac{e}{p - 1})}} \end{array}

Hence $v_{K} (\frac{x^{n}}{n!}) \to \infty$ as $n \to \infty$ . Thus $\exp (x)$ converges.

Since $v_{K} (\frac{x^{n}}{n!}) \geq r$ for all $n \geq 1$ , $\exp (x) \in 1 + π^{r} O_{K}$ .

Consider $\log$ : $1 + π^{r} O_{K} \to π^{r} O_{K}$ .

\log (1 + x) = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} x^{n}

which converges as before.

Recall identities in $ℚ [[X, Y]]$ :

\begin{array}{l} \exp (X + Y) & = \exp (X) \exp (Y) \\ \exp (\log (1 + X)) & = 1 + X \\ \log (\exp (X)) & = X \end{array}

Thus $\exp; (π^{r} O_{K}, +) \tilde{\to} (1 + π^{r} O_{K}, \times)$ is an isomorphism. □

$K$ any local field: $U_{K} : = O_{K}^{\times}$ , $π \in O_{K}$ uniformiser.

Definition 13.10 ( $s$ -th unit group). For $s \in ℤ$ , the $s$ -th unit group $U_{K}^{(s)}$ is defined by

U_{K}^{(s)} = (1 + π^{s} O_{K}, \times) .

Set $U_{K}^{(0)} = U_{K}$ . Then we have

\dots \subseteq U_{K}^{(s)} \subseteq U_{K}^{(s - 1)} \subseteq \dots \subseteq U_{K}^{(0)} = U_{K} .

Proposition 13.11.

(i) $U_{K}^{(0)} ∕ U_{K}^{(i)} ≅ (k^{\times}, \times)$ ( $k ≅ O_{K} ∕ π$ )
(ii) $U_{K}^{(s)} ∕ U_{K}^{(s + 1)} ≅ (k, +)$ for $s \geq 1$

Proof.

(i) Reduction modulo $π$ . $O_{K}^{\times} \to k^{\times}$ is surfective with kernel $1 + π O_{K} = U_{K}^{(1)}$ .
(ii) $f; U_{K}^{(s)} \to k$ , $1 + π^{s} x \mapsto x m o d π$ .
$(1 + π^{s} x) (1 + π^{s} y) = 1 + π^{s} (x + y + π^{s} x y) .$

$x + y + π^{s} x y \equiv x + y mod π$ , hence $f$ is a group homomorphism, surjective with kernel $U_{K}^{(s + 1)}$ .

□

Remark. Let $[K : ℚ_{p}] < \infty$ . Proposition 13.9, ?? implies that there exists finite index subgroup of $O_{K}^{\times}$ isomorphism to $(O_{K}, +)$ .

Example. $ℤ_{p}$ , $p > 2$ , $e = 1$ , take $r = 1$ . Then

\begin{array}{l} {ℤ_{p}}^{\times} & \tilde{\to} {(ℤ ∕ p ℤ)}^{\times} \times (1 + p ℤ_{p}) ≅ ℤ ∕ (p - 1) ℤ \times ℤ_{p} \\ x & \mapsto (x mod p, \frac{x}{[x mod p]}) \end{array}

$p = 2$ , take $r = 2$ .

\begin{array}{l} ℤ_{2}^{\times} & \tilde{\to} {(ℤ ∕ 4 ℤ)}^{\times} \times (1 + p^{2} ℤ_{p}) ≅ ℤ ∕ 2 ℤ \times ℤ_{2} \\ x & \mapsto (x mod 4, \frac{x}{𝜀 (x)}) \end{array}

where

𝜀 (x) = {\begin{matrix} + 1 & x \equiv 1 (m o d 4) \\ - 1 & x \equiv - 1 (m o d 4) \end{matrix}

So:

{ℤ_{p}}^{\times} ∕ {({ℤ_{p}}^{\times})}^{2} ≅ {\begin{matrix} ℤ ∕ 2 ℤ & if p > 2 \\ {(ℤ ∕ 2 ℤ)}^{2} & if p = 2 \end{matrix}

14 Higher Ramification Groups

Let $L ∕ K$ be a finite Galois extension of local fields, and $π_{L} \in O_{L}$ a uniformiser.

Definition 14.1 ( $s$ -th ramification group). Let $v_{L}$ be a normalised valuation in $O_{L}$ . For $s \in ℝ_{\geq - 1}$ , the $s$ -th ramification group is

G_{s} (L ∕ K) = {σ \in Gal (K) | v_{L} (σ (x) - x) \geq s + 1 \forall x \in O_{L}} .

Remark. $G_{s}$ only changes at integers.

$G_{s}$ , $s \in ℝ_{\geq - 1}$ used to define upper numbering.

Example.

\begin{array}{l} G_{- 1} (L ∕ K) & = Gal (L ∕ K) \\ G_{0} (L ∕ K) & = {σ \in Gal (L ∕ K) | σ (x) \equiv x mod π_{L} \forall x \in O_{L}} \\ = \ker (Gal (L ∕ K) ↠ Gal (k_{L} ∕ k)) \\ = I_{L ∕ K} \end{array}

Note. For $s \in ℤ_{\geq 0}$ ,

G_{s} (L ∕ K) = \ker (Gal (L ∕ K) ↠ Aut (O_{L} ∕ π_{L}^{s + 1} O_{L}))

hence $G_{s} (L ∕ K)$ is normal in $G_{- 1}$ .

\dots \subseteq G_{s} \subseteq G_{s - 1} \subseteq \dots \subseteq G_{- 1} = Gal (L ∕ K) .

Theorem 14.2.

(i) For $s \geq 1$ ,
$G_{s} = {σ \in G_{0} | v_{L} (σ (π_{L}) - π_{L}) \geq s + 1} .$
(ii) $⋂_{n = 0}^{\infty} G_{n} = {1}$ .
(iii) Let $s \in ℤ_{\geq 0}$ . Then there exists an injective group homomorphism
$G_{s} ∕ G_{s + 1} ↪ U_{L}^{(s)} ∕ U_{L}^{(s + 1)}$

induced by $σ \mapsto \frac{σ (π_{L})}{π_{L}}$ . This map is independent of the choice of $π_{L}$ .

Proof. Let $K_{0} \subseteq L$ be a maximal unramified extension of $K$ in $L$ . Upon replacing $K$ by $K_{0}$ , we may assume that $L ∕ K$ is totally ramified.

(i) Theorem 13.8 implies $O_{L} ∕ O_{K} [π_{L}]$ . Suppose $v_{L} (σ (π_{L}) - π_{L}) \geq s + 1$ . Let $x \in O_{L}$ , then $x = f (π_{L})$ , $f (X) \in O_{K} [X]$ . $\begin{array}{l} σ (x) - x & = σ (f (π_{L})) - f (π_{L}) \\ = f (σ (π_{L})) - f (π_{L}) \\ = (σ (π_{L}) - π_{L}) g (π_{L}) \end{array}$
for some $g (X) \in O_{K} [X]$ , using the fact that $X^{n} - Y^{n} = (X - Y) (X^{n - 1} + \dots + Y^{n - 1})$ . Thus
$v_{L} (σ (x) - x) = v_{L} (σ (π_{L}) - π_{L}) + \underset{\geq 0}{\underset{⏟}{v_{L} (g (π_{L}))}} \geq s + 1 .$
(ii) Suppose $σ \in Gal (L ∕ K)$ , $σ \neq 1$ . Then $σ (π_{L}) \neq π_{L}$ , because $L = K (π_{L})$ and hence $v_{L} (σ (π_{L}) - π_{L}) < \infty$ . Thus $σ \notin G_{s}$ for some $s ≫ 0$ by (i).

(iii) Note: for

σ \in G_{s}

s \in ℤ_{\geq 0}

σ (π_{L}) \in π_{L} + π_{L}^{s + 1} O_{L}

hence

\frac{σ (π_{L})}{π_{L}} \in 1 + π_{L}^{s} O_{L} = U_{L}^{(s)} .

We claim

\begin{array}{l} φ : G_{s} & \to U_{L}^{(s)} ∕ U_{L}^{(s + 1)} \\ σ & \mapsto \frac{σ (π_{L})}{π_{L}} \end{array}

is a group homomorphism with kernel $G_{s + 1}$ . For $σ, τ \in G_{s}$ , let $τ (π_{L}) = u π_{L}$ , $u \in O_{L}^{\times}$ . Then

\begin{array}{l} \frac{σ τ (π_{L})}{π_{L}} & = \frac{σ (τ (π_{L}))}{τ (π_{L})} \frac{τ (π_{L})}{π_{L}} \\ = \frac{σ (u)}{u} \frac{σ (π_{L})}{π_{L}} \frac{τ (π_{L})}{π_{L}} \end{array}

But $σ (u) \in u + π_{L}^{s + 1} O_{L}$ since $σ \in G_{s}$ . Thus $\frac{σ (u)}{u} \in U_{L}^{(s + 1)}$ and hence

\frac{σ τ (π_{L})}{π_{L}} \equiv \frac{σ (π_{L})}{π_{L}} \cdot \frac{τ (π_{L})}{π_{L}} mod U_{L}^{(s + 1)} .

Hence $φ$ is a group homomorphism. Moreover,

\ker (φ) = {σ \in G_{s} | σ (π_{L}) \equiv π_{L} mod π_{L}^{s + 1}} = G_{s + 1} .

If $π_{L}^{'} = a π_{L}$ is another uniformiser, $a \in O_{L}^{\times}$ . Then

\frac{σ (π_{L}^{'})}{π_{L}^{'}} = \frac{σ (a)}{a} \cdot \frac{σ (π_{L})}{π_{L}} \equiv \frac{σ (π_{L})}{π_{L}} mod U_{L}^{(s + 1)} . □

Corollary 14.3. $Gal (L ∕ K)$ is solvable.

Proof. By Proposition 13.11, Theorem 14.2 and Theorem 13.4, for $s \in ℤ_{\geq - 1}$ ,

G_{s} ∕ G_{s + 1} ≅ a subgroup {\begin{matrix} Gal (k_{L} ∕ k) & if s = - 1 \\ (k_{L}^{\times}, \times) & if s = 0 \\ (k_{L}, +) & if s \geq 1 \end{matrix}

Thus $G_{s} ∕ G_{s + 1}$ is solvable for $s \geq - 1$ . Conclude using Theorem 14.2(ii). □

Let $characteristic k = p$ . Then $p ∤ | G_{0} ∕ G_{1} |$ and $| G_{1} | = p^{n}$ . Thus $G_{1}$ is the unique (since normal) Sylow $p$ -subgroup of $G_{0} = I_{L ∕ K}$ .

Definition 14.4. $G_{1}$ is called the wild inertial group, and $G_{0} ∕ G_{1}$ is called the tame quotient.

Suppose $L ∕ K$ is finite separable. Say $L ∕ K$ is tamely ramified if $characteristic k ∤ e_{L ∕ K}$ . Otherwise it is wildly ramified.

Theorem 14.5. Assuming that:

$[K : ℚ_{p}] < \infty$
$L ∕ K$ finite
$D_{L ∕ K} = (π^{δ (L ∕ K)})$

Then

δ (L ∕ K) \geq e_{L ∕ K} - 1

, with equality if and only if tamely ramified. In particular,

L ∕ K

unramified if and only if

D_{L ∕ K} = O_{L}

Proof. Example Sheet 3 shows $D_{L ∕ K} = D_{L ∕ K_{0}} \cdot D_{K_{0} ∕ K}$ . Suffices to check $2$ cases:

(i) $L ∕ K$ unramified. Then ?? gives that $O_{L} = O_{K} [α]$ , for some $α \in O_{L}$ with $k_{L} = k (\bar{a})$ .
Let $g (X) \in O_{K} [X]$ be the minimal polynomial of $α$ . Since $[L : K] = [k_{L} : k]$ , we have that $\bar{g} (X) \in k [X]$ is the minimal polynomial of $\bar{a}$ . $\bar{g} (X)$ separable and hence $g^{'} (α) ⁄ \equiv 0 {(m o d π)}_{L}$ . Theorem 12.8 implies $D_{L ∕ K} = (g (α)) = O_{L}$ .

(ii)

L ∕ K

totally ramified. Say

[L : K] = e

O_{L} = O_{K} [π_{L}]

π_{L}

a root of

g (X) = X^{e} + \sum_{i = 0}^{e - 1} a_{i} X^{i} \in O_{K} [X]

is Eisenstein. Then

g^{'} (π_{L}) = \underset{\geq e - 1}{\underset{⏟}{e π_{L}^{e - 1}}} + \underset{v_{L} \geq e}{\underset{⏟}{\sum_{i = 1}^{e - 1} i a_{i} π_{L}^{i - 1}}} .

Thus $v_{L} (y^{'} (π_{L})) \geq e - 1$ . Equality if and only if $p ∤ e$ . □

Corollary 14.6. Suppose $L ∕ K$ is an extension of number fields. Let $P \subseteq O_{L}$ , $P \cap O_{K} = 𝔭$ . Then $e (P ∕ 𝔭) > 1$ if and only if $P | D_{L ∕ K}$ .

Proof. Theorem 12.9 implies $D_{L ∕ K} = \prod_{P} D_{L_{P} ∕ K_{𝔭}}$ . Then use $e (P ∕ 𝔭) = e_{L_{P} ∕ K_{𝔭}}$ and Theorem 14.5. □

Example.

$K = ℚ_{p}$ , $ζ_{p^{n}}$ a primitive $p^{n}$ -th root of unity. $L = ℚ_{p} (ζ_{p^{n}})$ . The $p^{n}$ -th cyclotomic polynomial is
$Φ_{p^{n}} (X) = X^{p^{n - 1} (p - 1)} + X^{p^{n - 1} (p - 2)} + \dots + 1 \in ℤ_{p} [X] .$

See Example Sheet 3.
$Φ_{p^{n}} (X)$ irreducible (hence $Φ_{p^{n}} (X)$ is the minimal polynomial of $ζ_{p^{n}}$ ).
$L ∕ ℚ_{p}$ is Galois, totally ramified of degree $p^{n + 1} (p - 1)$ .
$π : = ζ_{p^{n}} - 1$ a uniformiser in $O_{L}$ $⇝$ $O_{L} = ℤ_{p} [ζ_{p^{n}} - 1] = ℤ_{p} [ζ_{p^{n}}]$ .

$Gal (L ∕ ℚ_{p}) \tilde{\to} {(ℤ ∕ p^{n} ℤ)}^{\times}$ (abelian). $σ_{m} \leftrightarrow m$ where $σ_{m} (ζ_{p^{n}}) = ζ_{p^{n}}^{m}$ .

v_{L} (σ_{m} (π) - π) = v_{L} (ζ_{p^{n}}^{m} - ζ_{p^{n}}) = v_{L} (ζ_{p^{n}}^{m - 1} - 1) .

Let $k$ be maximal such that $p^{k} | m - 1$ . Then $ζ_{p^{n}}^{m - 1}$ is a primitive $p^{n - k}$ -th root of unity, and hence $ζ_{p^{n}}^{m - 1} - 1$ is a uniformiser $π^{'}$ in $L^{'} = ℚ_{p} (ζ_{p^{n}}^{m - 1})$ . Hence

v_{L} (ζ_{p^{n}}^{m - 1} - 1) = e_{L ∕ L^{'}} = \frac{e_{L ∕ ℚ_{p}}}{e_{L^{'} ∕ ℚ_{p}}} = \frac{[L : ℚ_{p}]}{[L^{'} : ℚ_{p}]} = \frac{p^{n - 1} (p - 1)}{p^{n - k - 1} (p - 1)} = p^{k} .

Theorem 14.2(i) implies that $σ_{m} \in G_{i}$ if and only if $p^{k} \geq i + 1$ . Thus

G_{i} ≅ {\begin{matrix} {(ℤ ∕ p^{n} ℤ)}^{\times} & i \leq 0 \\ (1 + p^{k} ℤ) ∕ p^{n} ℤ & p^{k - 1} - 1 < i \leq p^{k} - 1 (1 \leq k \leq i + 1) \\ {1} & p^{n - 1} - 1 < i \end{matrix} .

Part VI
Local Class Field Theory

15 Infinite Galois Theory

Definition 15.1 (Infinite Galois definitions).

$L ∕ K$ is separable if $\forall α \in L$ , the minimal polynomial $f_{α} (X) \in K [X]$ for $α$ is separable.
$L ∕ K$ is normal if $f_{α} (X)$ splits in $L$ for all $α \in L$ .
$L ∕ K$ is Galois if it is separable and normal. Write $Gal (L ∕ K) : = {Aut}_{K} (L)$ in this case. If $L ∕ K$ is a finite Galois extension, then we have a Galois correspondence:
$\begin{array}{l} {subextensions K \subseteq K^{'} \subseteq L} & \leftrightarrow {subgroups of Gal (L ∕ K)} \\ K^{'} & \mapsto Gal (K ∕ K^{'}) \end{array}$

Let $(I, \leq)$ be a poset. Say $I$ is a directed set if for all $i, j \in I$ , there exists $k \in I$ such that $i \leq k$ , $j \leq k$ .

Example.

Any total order (for example $(ℕ, \leq)$ ).
$ℕ_{\geq 1}$ ordered by divisibility.

Definition 15.2. Let $(I, \leq)$ be a directed set and ${(G_{i})}_{i \in I}$ a collection of groups together with maps $φ_{i j} : G_{j} \to G_{i}$ , $i \leq j$ such that:

$φ_{i k} = φ_{i j} \circ φ_{j k}$ for any $i \leq j \leq k$
$φ_{i i} = id$

Say $({(G_{i})}_{i = 1}, φ_{i j})$ is an inverse system. The inverse limit of $(G_{i}, φ_{i})$ is

\lim_{\overset{[}{i}] \leftarrow} G_{i} = {{(g_{i})}_{i \in I} \in \prod_{i \in I} G_{i} | φ_{i j} (g_{j}) = g_{i}} .

Remark.

$(ℕ, \leq)$ recovers the previous set.
There exist projection maps $φ_{j} : \lim_{\overset{[}{i} \in I] \leftarrow} G_{i} \to G_{j}$ .
$\lim_{\overset{[}{i} \in I] \leftarrow} G_{i}$ satisfies a universal property.
Assume $G_{i}$ finite. Then the profinite topology on $\lim_{\overset{[}{i} \in I] \leftarrow} G_{i}$ is the weakest topology such that $φ_{j}$ are continuous for all $j \in I$ .

Proposition 15.3. Assuming that:

$L ∕ K$ Galois

Then

(i) The set $I = {F ∕ K finite | F \subseteq L, F Galois}$ is a directed set under $\subseteq$ .
(ii) For $F, F^{'} \in I$ , $F \subseteq F^{'}$ there is a restriction map ${res}_{F, F^{'}} : Gal (F^{'} ∕ K) ↠ Gal (F ∕ K)$ and the natural map
$Gal (L ∕ K) \to \lim_{\overset{[}{F} \in I] \leftarrow} Gal (F ∕ K)$

is an isomorphism.