Example. :
In general:
Combinatorics
Lectured by Imre Leader
Example.
Example. :

In general:

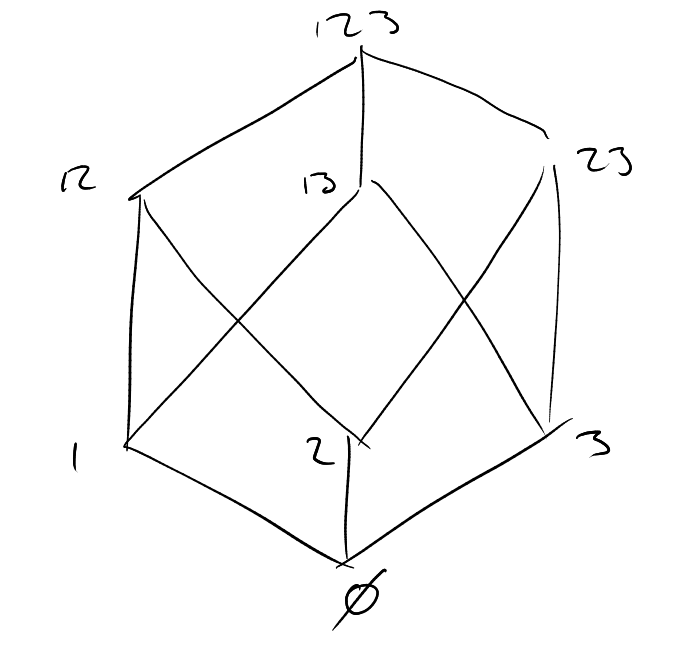
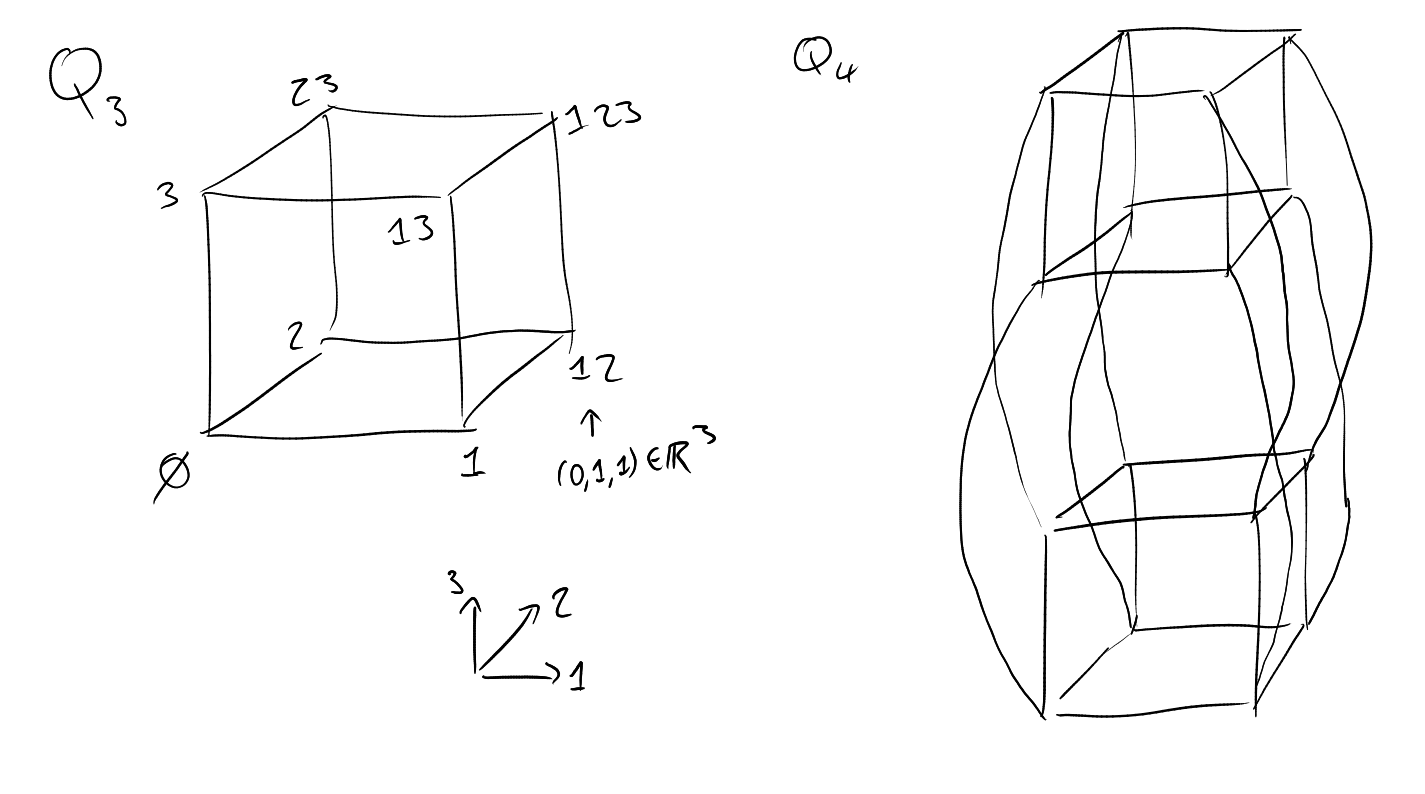
Alternatively, can view as an -dimensional unit cube , by identifying e.g. with (i.e. identify with , the characteristic function of ).
Example.
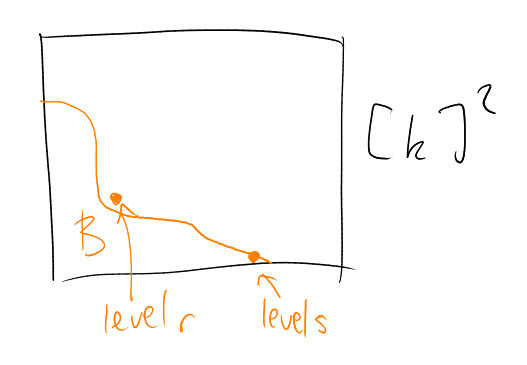
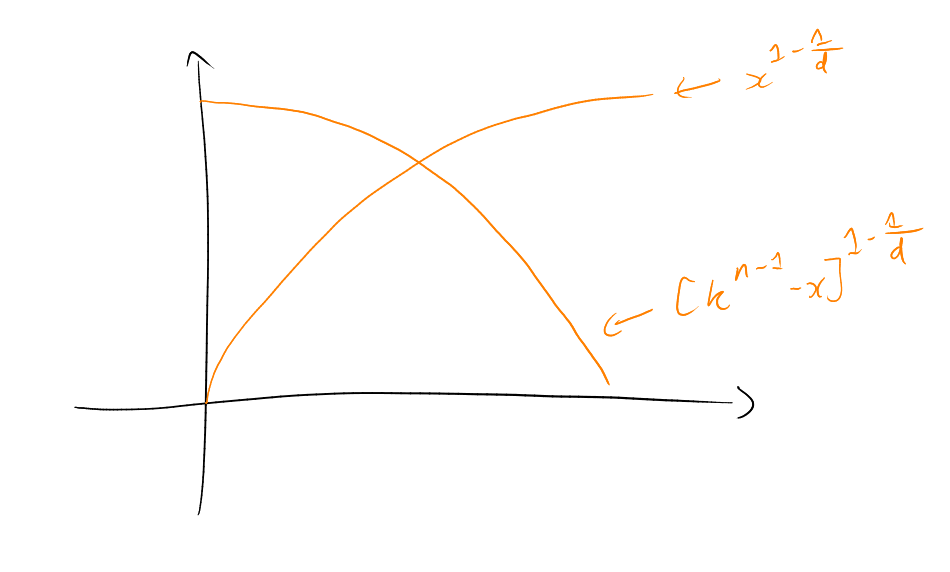
How large can a chain be? Can achieve , for example using
Cannot beat this: for each , contains -set.
How large can an antichain be? Can achieve , for example . More generally, can take , for any – best out of these is .
Can we beat this?
Idea: Motivated by “a chain meets each layer in point, because a layer is an antichain”, we will try to decompose the cube into chains.
Proof. We’ll decompose into chains – then done. To achieve this, it is sufficient to find:
We then put these together to form our chains, each passing through .
By taking complements, it is enough to prove (i).
Let be the (bipartite) subgraph of spanned by : we seek a matching from to . For any , the number of edges in is (counting from below) and (counting from above).
Hence, as ,
Thus by Hall’s Marriage theorem, there exists a matching. □
Equality in Sperner’s Lemma? Proof above tells us nothing.
Aim: If is an antichain then
“The percentages of each layer occupied add up to .”
Trivially implies Sperner’s Lemma (think about it).
Example. If , then .
“The fraction of the level occupied by is the fraction for ”.
Remark. LYM = Lubell, Meshalkin, Yamamoto.
Proof. The number of edges in is (counting from above) and is (counting from above). So
But , so done. □
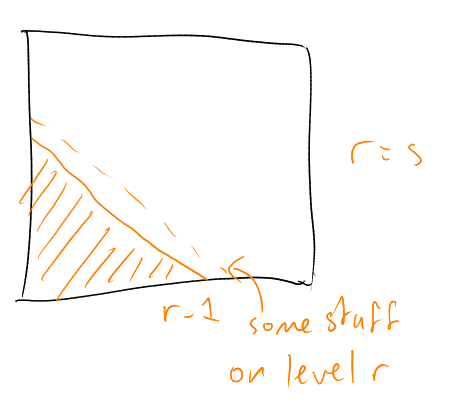
Equality in Local LYM? Must have that , , have . So or .
Proof 1. “Bubble down with Local LYM”.
Have . Now, and disjoint (as is an antichain), so
whence
by Local LYM.
Now, note is disjoint from (since is an antichain), so
whence
(Local LYM) so
Continue inductively. □
Equality in LYM Inequality? Must have had equality in each use of Local LYM. Hence equality in LYM Inequality needs: max with has .
So: equality in Local LYM for some .
Hence: equality in Sperner’s Lemma if and only if (if even), and or .
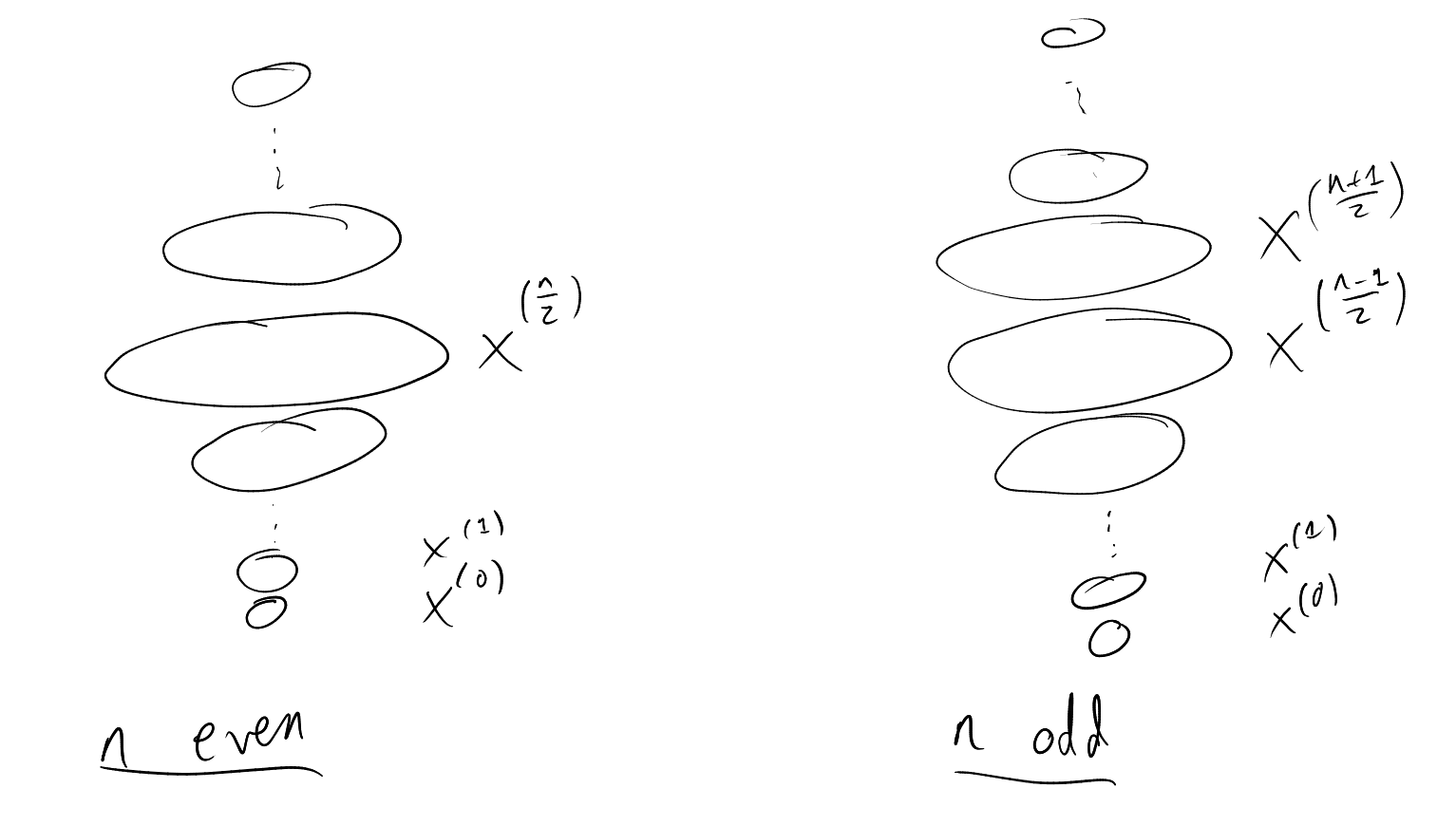
Proof 2. Choose, uniformly at random, a maximal chain (i.e. , with for all ).
For any -set , (all -sets are equally likely). So (as events are disjoint) and hence
Equivalently: (if you want to lose the intuition about how this works) then: , and , hence
For , know . Equality is rare – only for or . What happens in between?
In other words, given , how should we choose to minimise ?
Believable that if then we sholud take .
What if ?
Believable that should take plus some -sets in . For example, for with , take .
Let and be distinct -sets: say , where and .
Say that in the lexicographic (or lex) ordering if for some we have for and .
Slogan: “Use small elements” (“dictionary order”).
Example. lexicographic on : .
lexicographic on : , .
Say that in the colexicographic (or colex) ordering if for some we have for all and .
Slogan: “Avoid large elements” (note that this is not quite the same as “use small elements”, which is what we had before).
Example. colexicographic on : .
colexicographic on : , .
Note that, in colexicographic, is an initial segment (first elements, for some ) of .
This is false for lex.
So we could view colexicographic as an enumeration of .
Remark. in colexicographic if and only if in “lexicographic with ground set order reversed”.
Aim: colexicographic initial segments are best for , i.e. if and is the initial segment of colexicographic with , then .
In particular, .
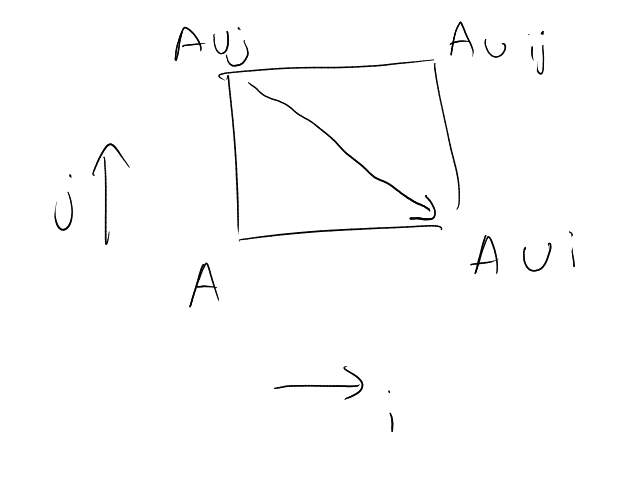
Idea: try to transform into some such that:
Ideally, we’d like a family of such ‘compressions’: such that either or is so similar to that we can directly check that .
“colexicographic prefers 1 to 2” inspires:
Note that the second part of the union in is because we need to make sure that we “replace by where possible”.
Example. If then .
So , and .
Say is -compressed if .
Proof. Write for . Let . We’ll show that , and . [Then done].
Have for some , with (as ). So , , and .
Cannot have , else , giving , contradiction.
Hence we have , .
Also, , since .
Suppose : so for some . Cannot have , else – so (as ), contradicting . Hence and .
Whence both and belong to (by definition of ), contradicting . □
Remark. Actually showed that .
Proof. Define a sequence as follows. Set . Having defined , if left-compressed then stop the sequence with .
If not, choose such that is not -compression, and set .
This must terminate, because for example is strictly decreasing in .
Final term satisfies , and (by Lemma 10) □
Remark.
These compressions only encode the idea “colexicographic prefers to ()”, but this is also true for lexicographic.
So we try to come up with more compressions that encode more of what colexicographic likes.
“colexicographic prefers to ” inspires:
Example. If
then
So , and .
Say is -compressed if .
Sadly, we can have :
Example. has , but has .
Despite this, we at least we do have the following:
Proof. Suppose not. So there exists with , in colexicographic but , .

Put , .
Then , and disjoint, and (since , by definition of colexicographic).
So , contradicting is -compression. □
Proof. Let . For , we’ll show , , and . (Then done).
Have for some , and , so , , and (by definition of ).
If : there exists such that is -compressed, so from we have – contradicting , contradiction.
Thus , and so , . Certainly (because ), so just need to show that .
Suppose : so , for some . Also have (for example, as contained in it).
If : know is -compressed for some , so – contradicting .
If : have , , so by definition of we must have that both and – contradicting , a contradiction. □
Theorem 16 (Kruskal-Katona). Assuming that:
Proof. Let . Define a sequence of set systems in as follows:
Set .
Having chosen , if is -compressed for all then stop. Otherwise, choose with minimal such that is not -compressed.
Note that such that (namely, use ). So () is satisfied.
So Lemma 15 tells us that .
Set , and continue.
Must terminate, as is strictly decreasing. The final term satisfies , and is -compressed for all .
So by Lemma 14. □
Remark.
where , and , then
For , , the upper shadow of is
Proof. From Kruskal-Katona, since in colexicographic if and only if in lexicographic with ground-set order reversed. □
Note that the shadow of an initial segment of colexicographic on is an initial segment of colexicographic on – as if then .
This fact gives:
Proof. If , then , because is an initial segment of colexicographic. Done by induction. □
Note. If , then .
Remark. Proof of Kruskal-Katona used Lemma 14 and Lemma 15, but not Lemma 10 or Corollary 12.
How large can an intersecting family be? Can have , by taking .
Proof. For any , at most one of can belong to . □
Note. Many other extremal examples. For example, for odd take .
What if ?
If , take .
If : just choose one of for all : gives .
So interesting case is .
Could try . Has size (while this identity can be verified by writing out factorials, a more useful way of observing it is by noting that ).
Could also try .
Example. , . Then and
Proof 1 (“Bubble down with Kruskal-Katona”). Note that .
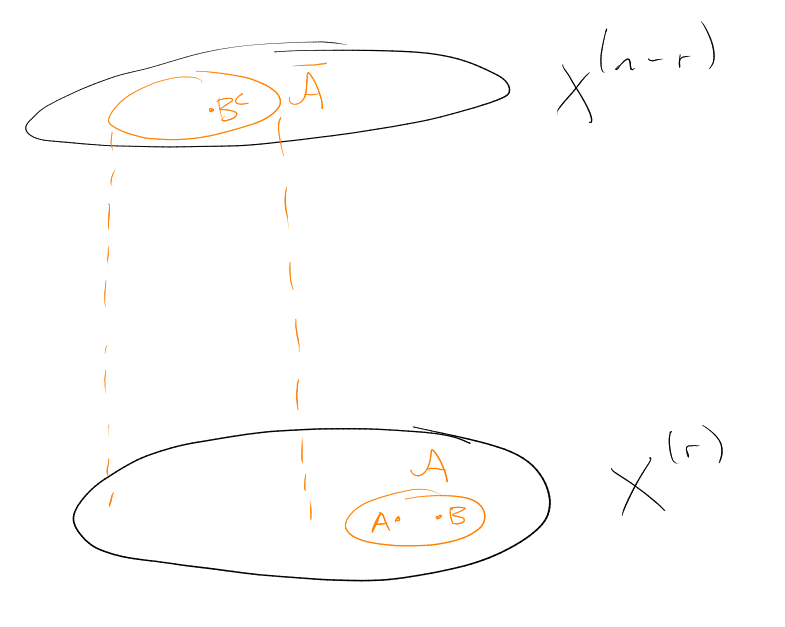
Let . Have and are disjoint families of -sets.
Suppose . Then . Whence by Kruskal-Katona we have .
So , a contradiction. □
Remark. Calculation at the end had to give the right answer, as the calculations would all be exact if .
Proof 2. Pick a cyclic ordering of i.e. a bijection .
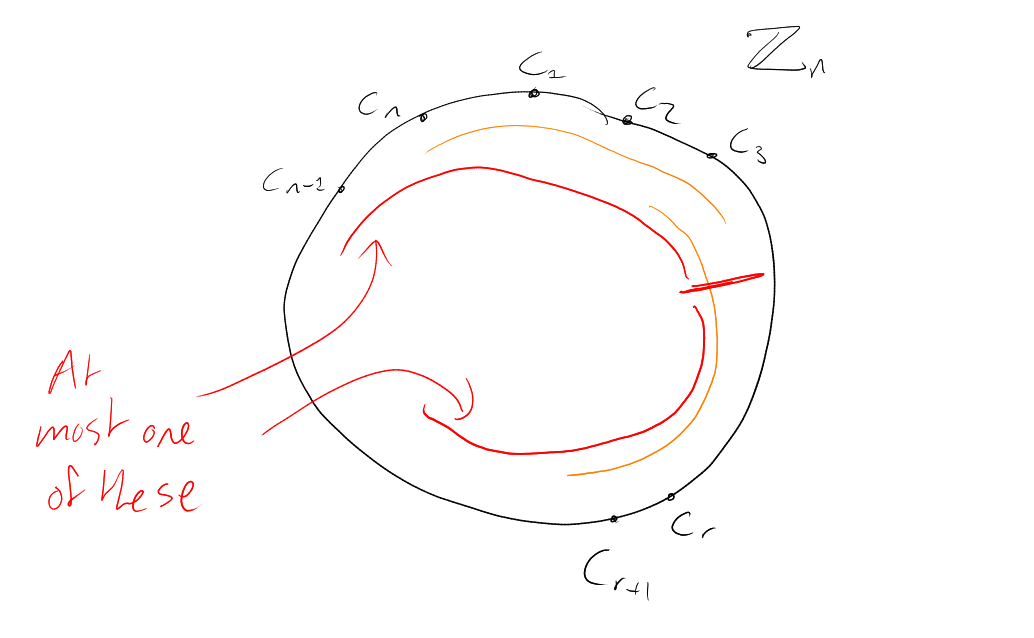
How many sets in are intervals ( consecutive elements) in this ordering?
Answer: . Because say . Then for each , at most one of the two intervals and can belong to (subscrpits are modulo ).
For each -set , in how many of the cyclic orderings is it an interval?
Answer: ( where, order inside , order outside ).
Hence , i.e. . □
Remark.
Can get this from Proof 1 (and equality in Kruskal-Katona) or from Proof 2 (with a bit of care).
“How do we minimise the boundary of a set of given size?”
Example. Among all subsets of of given area, the disc minimises the perimeter.
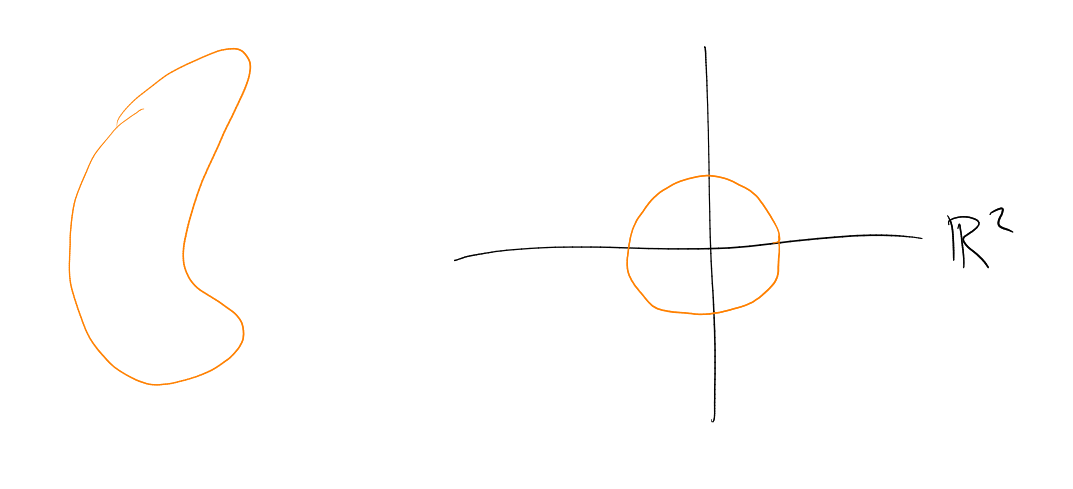
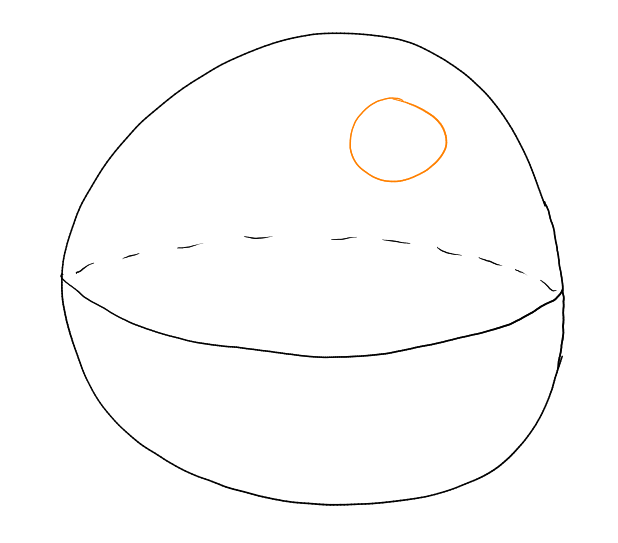
Among all subsets of of given volume, the solid sphere minimises the surface area.

Among all subsets of of given surface area, the circular arc has the smallest perimeter.
Example. Here, if , then .
Definition (Isoperimetric inequality). An isoperimetric inequality on is an inequality of the form
for some function .
A good example for might be a ball . What happens for ?
Example. in .
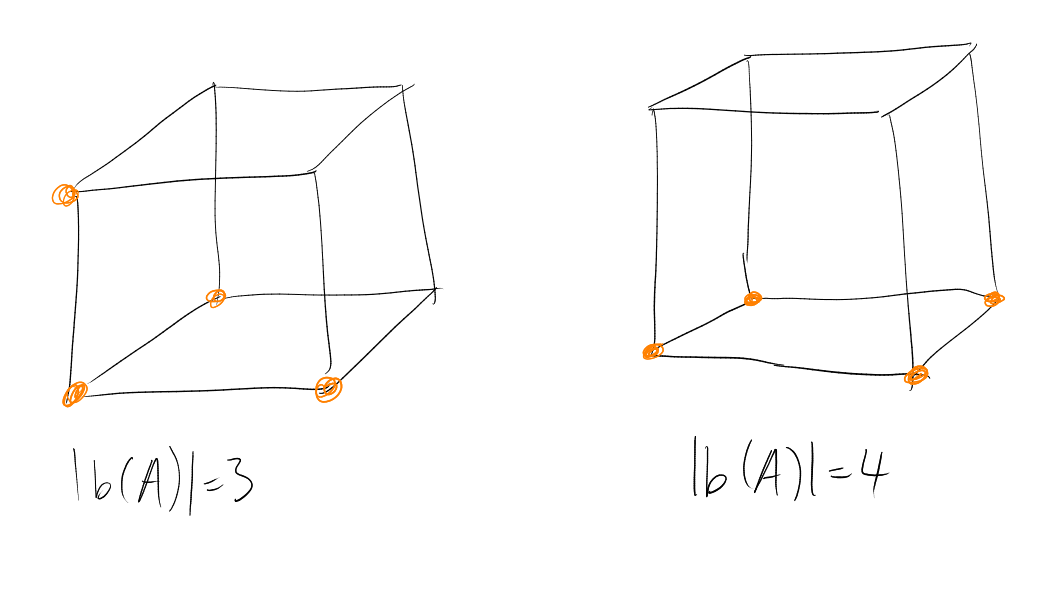
Good guess that balls are best, i.e. sets of the form .
What if ?
Guess: take with . If , where , then . So we’d take to be an initial segment of lexicographic (by Kruskal-Katona).
This suggests...
In the simplicial ordering on , we set if either or and in lexicographic.
Aim: initial segments of simplicial ordering minimise the boundary.
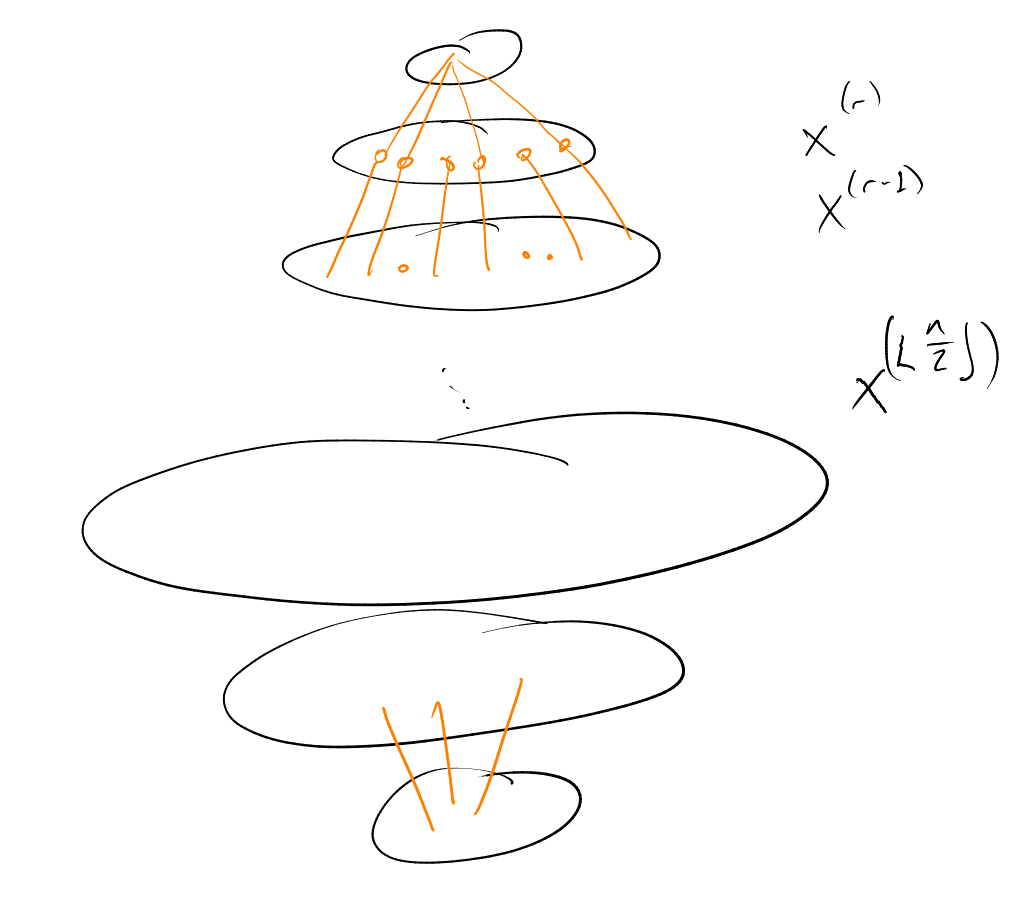
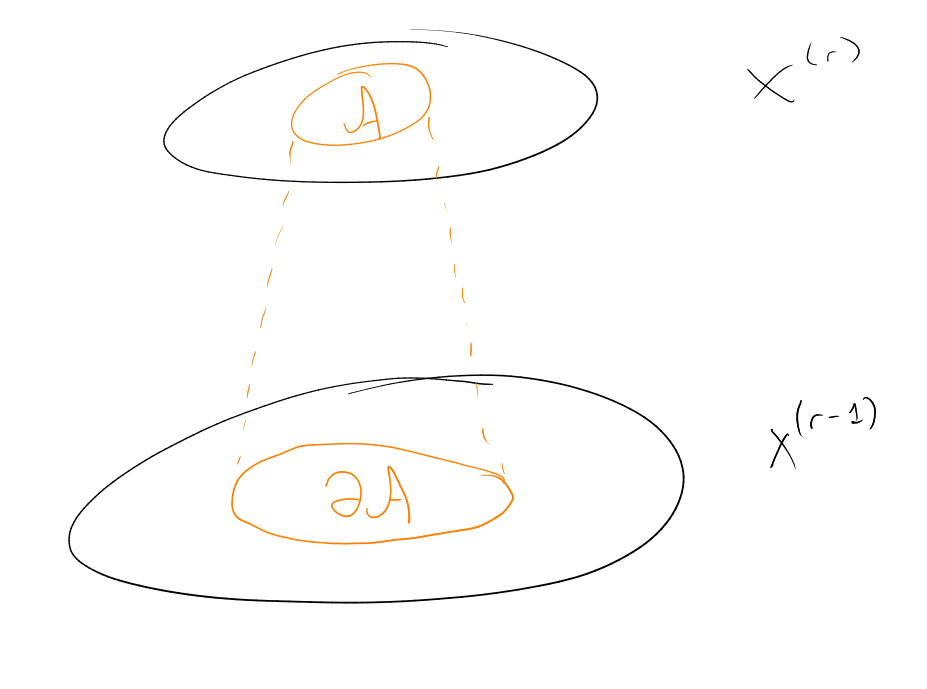
Definition (-sections). For and , the -sections of are the families given by:
The -compression of in the family given by:
is the first elements of simplicial ordering on
is the first elements of simplicial ordering on
Theorem 1 (Harper’s Theorem). Assuming that:
Remark.
Proof. Induction on : is trivial.
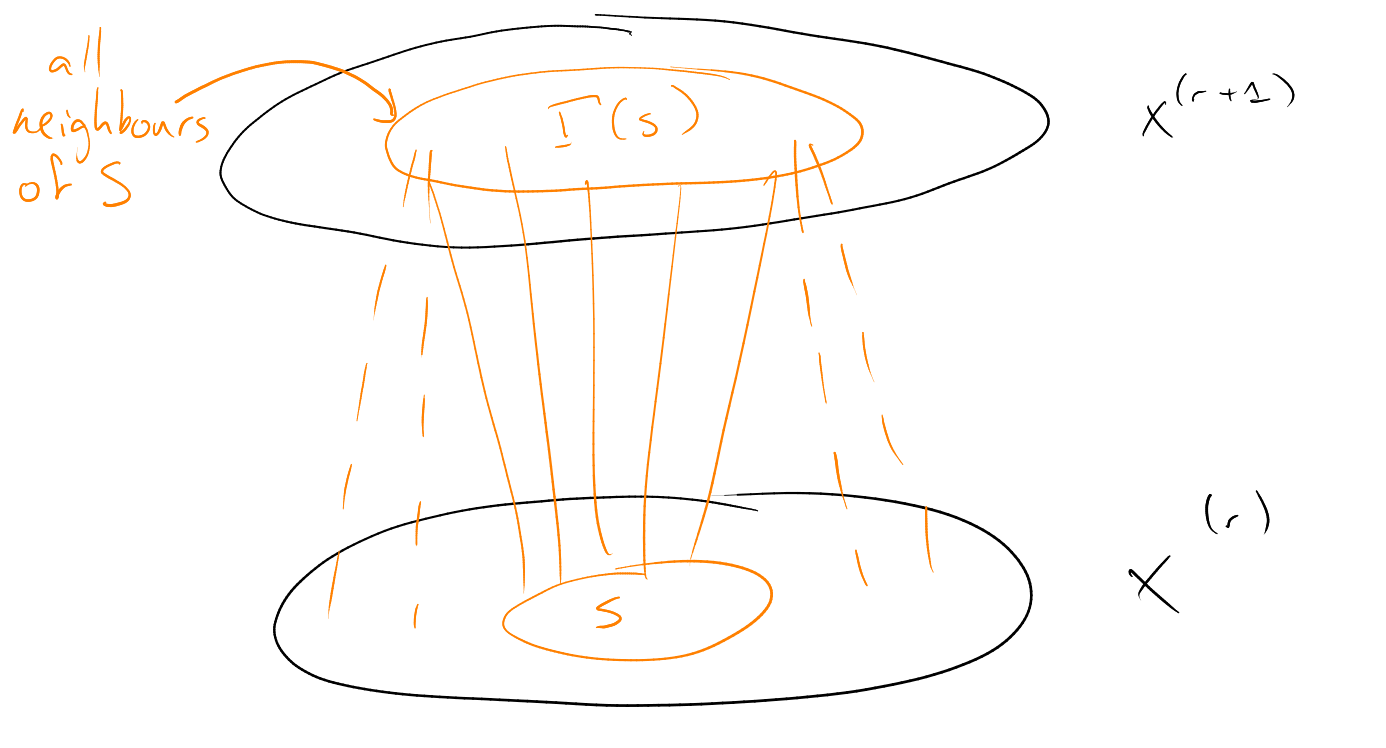
Given , and , and .
Claim: .
Proof of claim: Write for . We have
and of course
Now, and (by the induction hypothesis). But is an initial segment of simplicial ordering, and is an initial segment of simplicial ordering (as neighbourhood of initial segment is an initial segment).
So then and are nested (one conatined in the other). Hence . Similarly, .
Hence , which completes the proof of our claim. □
Define a sequence as follows:
Set .
Having chosen : if is -compressed with and set – and continue.
Must terminate, because is strictly decresing.
The final family satisfies , , and is -compressed for all . Does -compressed for all imply that is an initial segment of simplicial ordering? (If yes, then and we are done).
Sadly, no. For example in can take :
However:
either is odd, say , and
or is even, say , and .
For the even case: “Remove the last -set with , and add the first -set without .”
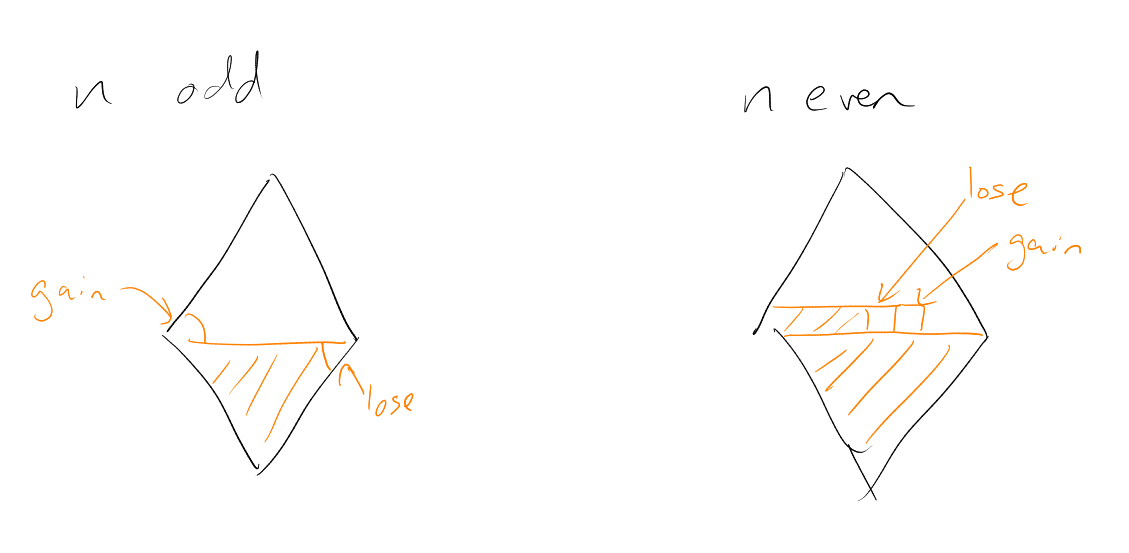
After we prove this, we will have solved our problem, as in each case we certainly have .
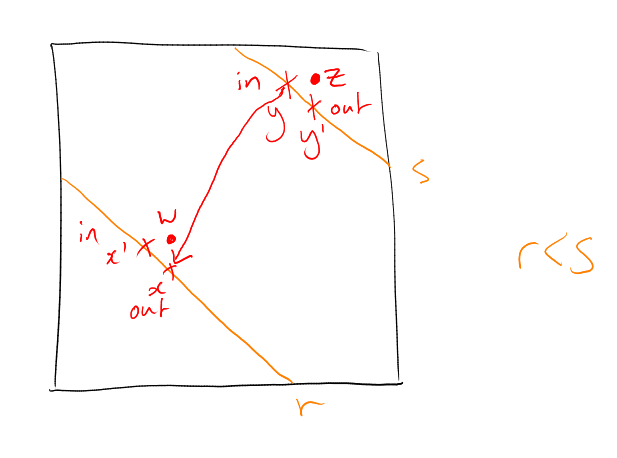
Proof. Since is not an initial segment of simplicial ordering, there exists (in simplicial ordering) with , .
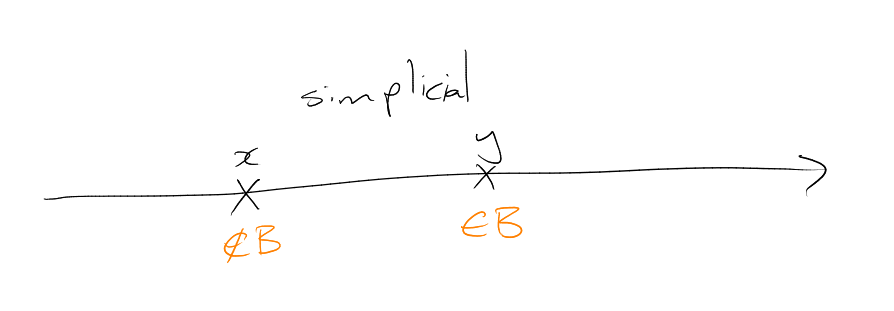
For each : cannot have , (as is -compressed). Also cannot have , for the same reason.
So .
Thus: for each , there exists at most one earlier with (namely ). Similarly, for each there is at most one later with (namely ).
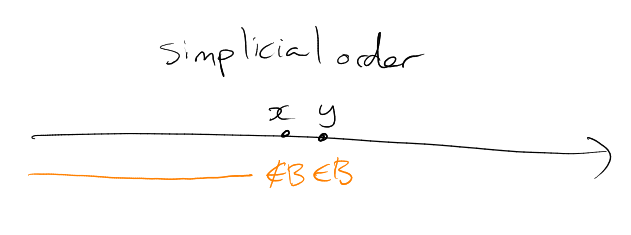
So , with the predessor of and .
Hence if then is the last -set, and if then is the last -set with . □
Proof of Theorem 1. Done by above. □
Remark.
For and , the -neighbourhood of is .
Proof. Theorem 1 with induction on . □
To get a feeling for the strength of Corollary 3, we’ll need some estimates on things like .
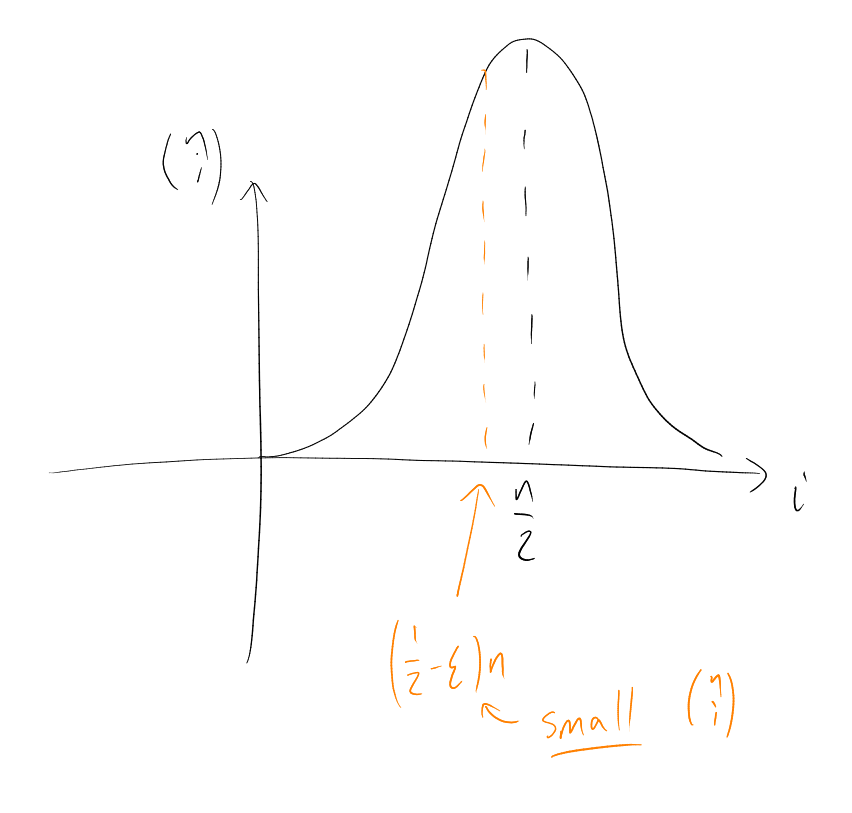
“Going standard deviations away from the mean .”
“For fixed, , this is an exponentially small fraction of .”
Proof. For :
so
Hence
(sum of a geometric progression).
Same argument tells us that
Thus
“-sized sets have exponentially large -neighbourhoods.”
Remark. Same would show, for “small” sets:
Say is Lipschitz if for all adjacent.
For , say is a Lévy mean or median of if
and
Now ready to show “every well-behaved function on the cube is roughly constant nearly everywhere”.
Note. This is the “concentration of measure” phenomenon.
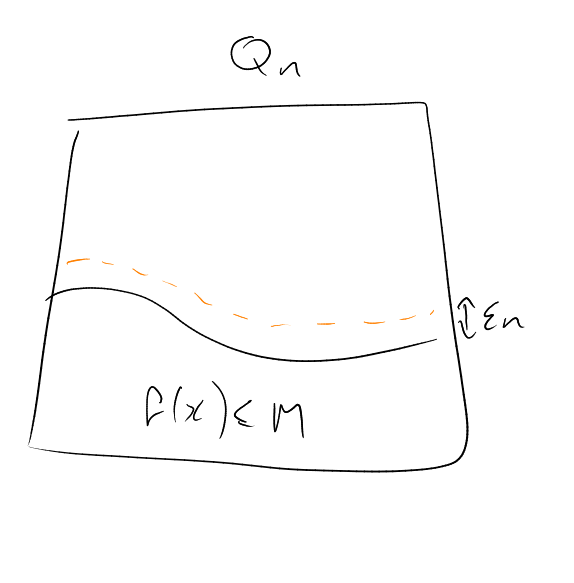
Let be a graph of diameter ().
So Theorem 5 tells us that the sequence is a Lévy family – even a normal Lévy family, meaning grows exponentially small in , for each .
So have concentration of measure for any Lévy family.
Many naturally-occurring families of graphs are Lévy families.
Example. , where is made into a graph by joining to if is a transposition.
Can define similarly for any metric measure space (of finite measure and finite diameter).
Example. is a Lévy family.
Two ingredients:
Proof by compression:

This complement has measure about , which as .
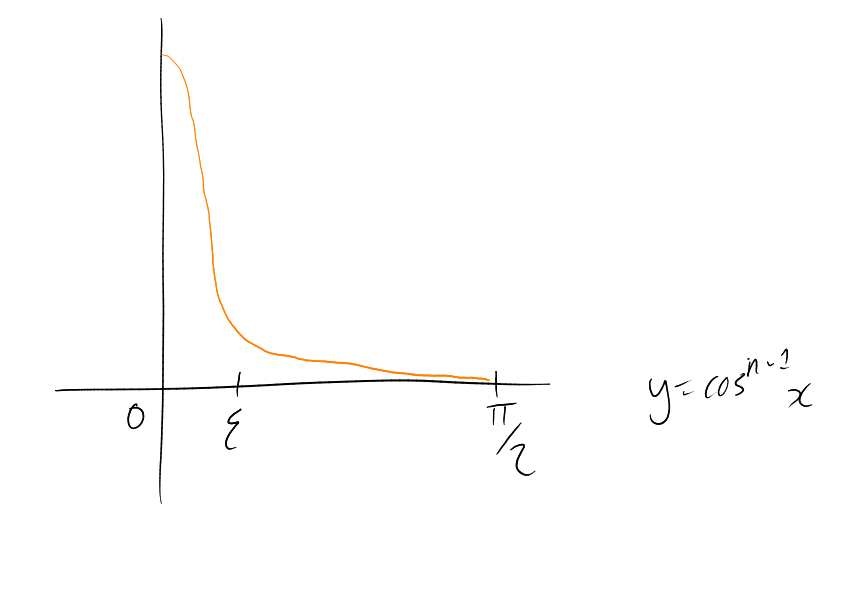
We deduced concentration of measure from an isoperimetric inequality.
Conversely:
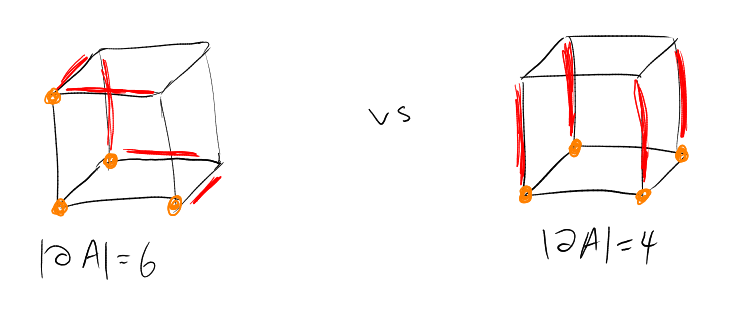
For a subset of vertices of a graph , the edge-boundary of is
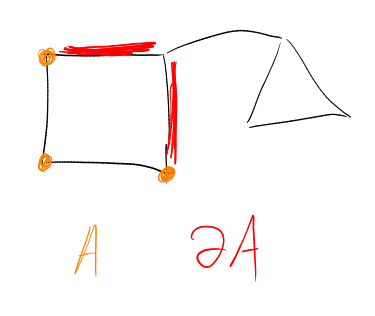
An inequality of the form: for all is an edge-isoperimetric inequality on .
What happens in ? Given , which should we take, to minimise ?
Example. in :
This suggests that maybe subcubes are best.
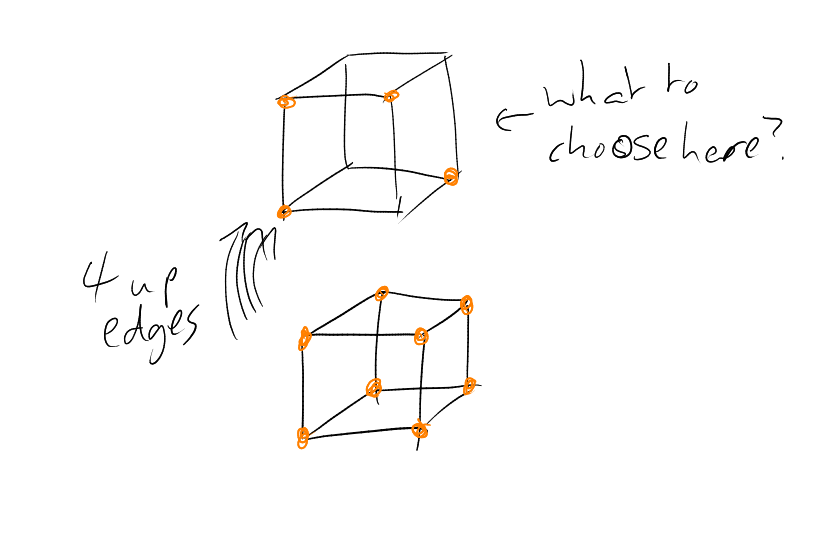
What if ? with ? Natural to take . Suppose we are in , and considering , eg . We might take the whole of the bottom layer, and then stuff in the upper layer. Note that the size of the boundary will be the number of up edges (which is , a constant), plus the number of edges in the top layer. So we just want to minimise the number of edges in the top layer, i.e. find with with minimal boundary.
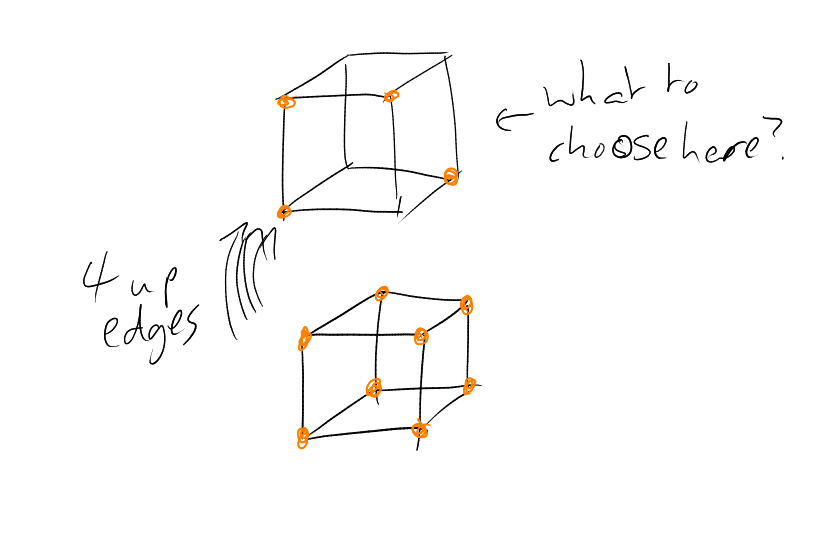
So we define: for , , say in the binary ordering on if . Equivalently, if and only if . “Go up in subcubes”.
Example. In : .
For , , we define the -binary compression by giving its -sections:
so . Say is -binary compressed if .
Remark. Sometimes called the “Theorem of Harper, Lindsey, Bernstein & Hart”.
Proof. Induction on . trivial.
For , , :
Claim: .
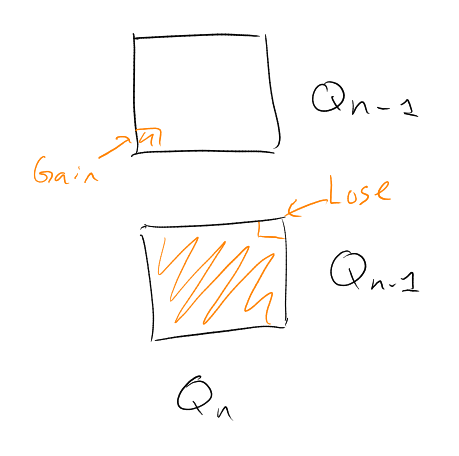
Proof of claim: write for . .image Have
Now, and (induction hypothesis). Also, the sets and are nested (one is contained inside the other), as each is an initial segment of binary on .
Whence we certainly have . So .
Define a sequence as follows: set . Having defined , if is -binary compressed for all then stop the sequence with . If not, choose with and put . Must terminate, as the function is strictly decreasing.
The final family satisfies , , and is -binary compressed for all .
Note that need not be an initial segment of binary, for example .
However:
(Then done, as clearly , since ).
Proof. As not an initial segment, there exists with , . Then for all : cannot have , and cannot have (as is -binary compressed).
Thus for each , there exists at most 1 earlier (namely ). Also for each there is at most one later (namely ).
Then and adjacent (since is the unique element in after , and is the unique element not in before ).
So , where is the predecessor of and .
So must have . □
This concludes the proof of Theorem 8. □
The isoperimetric number of a graph is
is the “average out-degree of ”.
Proof. Taking , we show (as ).
To show , just need to show that if is an initial segment of binary with then .
But , so certainly . □
For any , the grid is the graph on in which is joined to if for some we have for all and .
“distance is -distance”.
Example.
Note that for this is exactly .
Do we have analogues of Theorem 1 and Theorem 8 for the grid?
Starting with vertex-isoperimetric: which sets (of given size) minimise ?
Example. In :
For : .
For : .
This suggests we “go up in levels” according to – e.g. we’d take .
What if ?
Guess: take plus some points with , but which points?
Example. In :
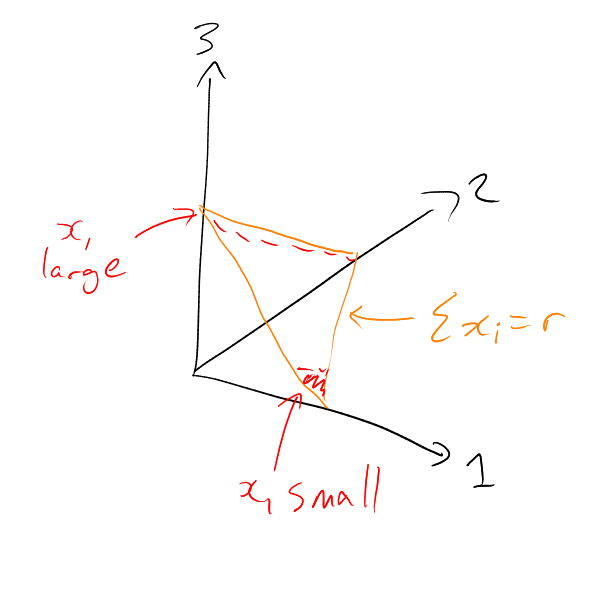
so “keep large”.
This suggests in the simplicial order on , we set if either or and , where .
Note. Agrees with the previous definition of simplicial ordering when .
Example. On : , , , , , , , , .
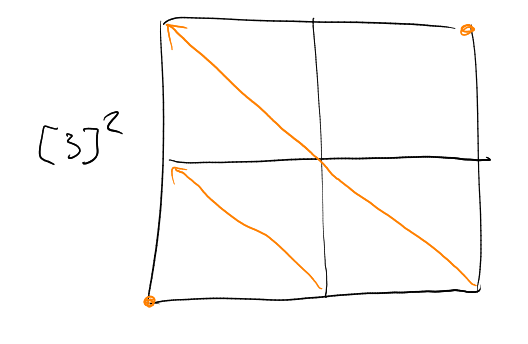
On : , , , , , , , , , , , , …
r (), and , the -sections of are the sets (or ) as a subset of defined by:
for each .
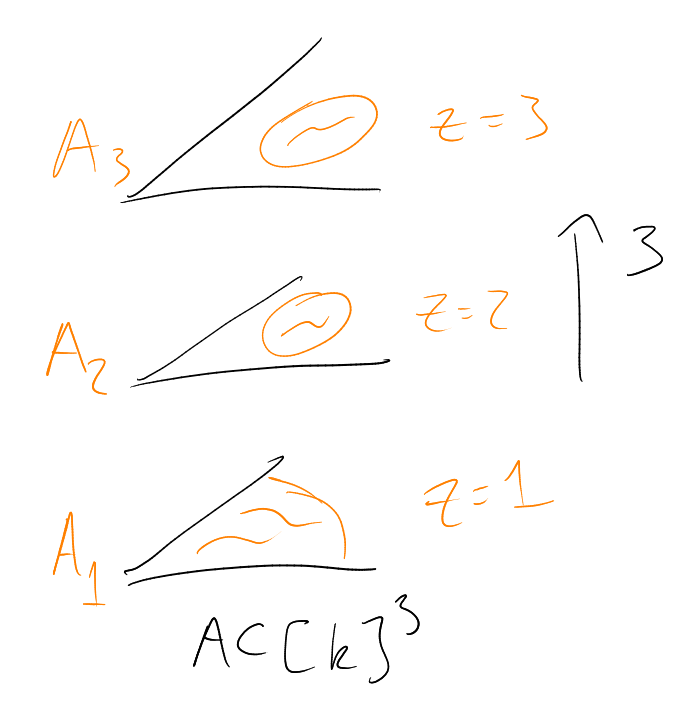
The -compression of is is defined by giving its -sections:
Thus .
Theorem 11 (Vertex-isoperimetric inequality in the grid). Assuming that:
Proof. Induction on . For it is trivial: if , then .
Given and : fix .
Claim: .
Proof of claim: write for . For any , we have

(where ).
Also,
Now, and , and (induction hypothesis). But the sets , , are nested (as each is an initial segment of simplicial order on ).
Hence for each . Thus .
Among all with and , pick one that minimises the quantity .
Then is -compressed for all . Note however, that this time we will make use of this minimality property of for more than just deducing that is -compressed for all .
Case 1: . What we know is precisely that is a down-set ( is a down-set if , )
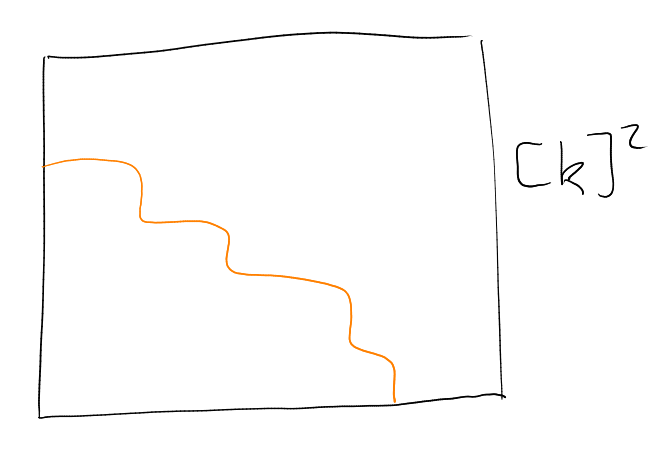
Let and . May assume , since implies would imply .
If : then . So clearly .
If : cannot have , because then also (as is a down-set).
So there exists with , , and (, ).
Similarly, cannot have , because then (as is a down-set). So there exists with , , and . Now let . From we lost point in the neighbourhood (namely in the picture), and gained point (the only point that we can possibly gain is ), so . This contradicts minimality of . This finishes the two dimensional case.
Case 2: . For any and any with , . Have (as is -compressed for any , so apply with some ). So, considering the -sections of , we have for all .
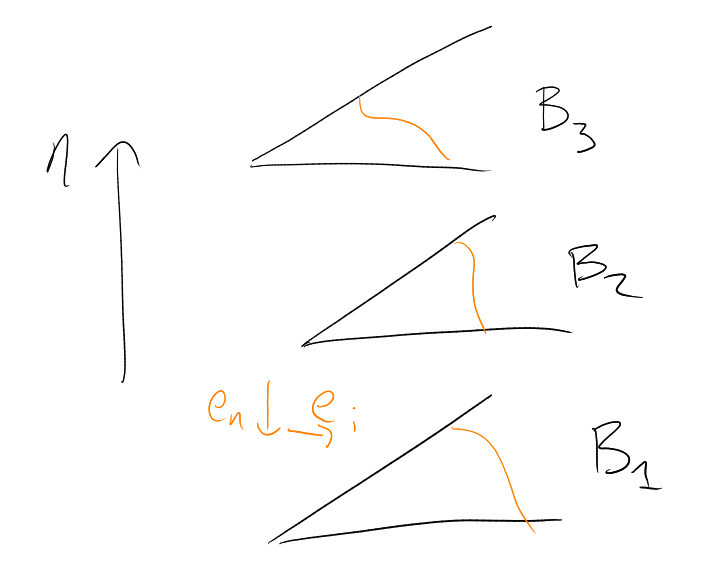
Recall that . So in fact for all . Thus
Similarly,
So to show , enough to show that and .
: define a set as follows: put , and for set . Then , so . Also, is an initial segment of simplicial order. So in fact , whence .
: define a set as follows: put and for set ( is the biggest it could be given ). Then , so . Also, is an initial segment of simplicial order. So , whence . □
Remark. Can check from Corollary 12 that, for fixed, the sequence is a Lévy family.
Which set (of given size) should we take to minimise ?
Example. In :
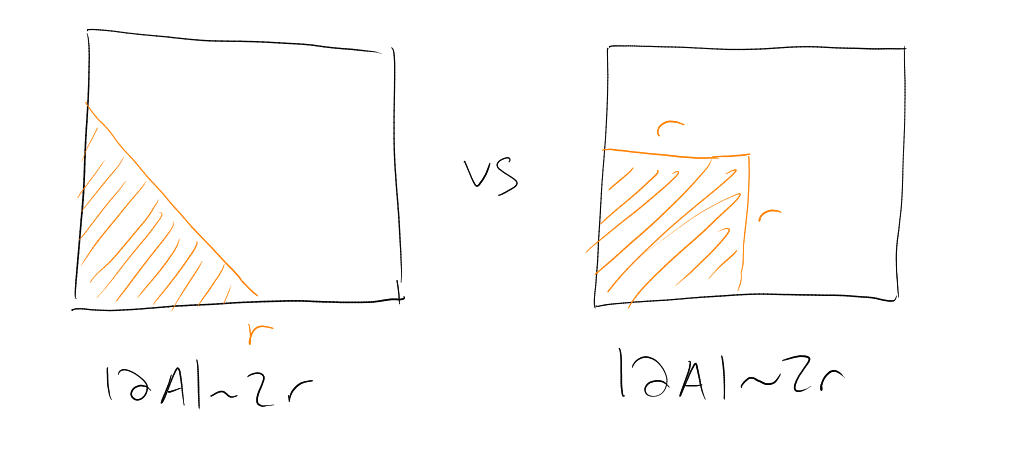
Suggests squares are best.
However...
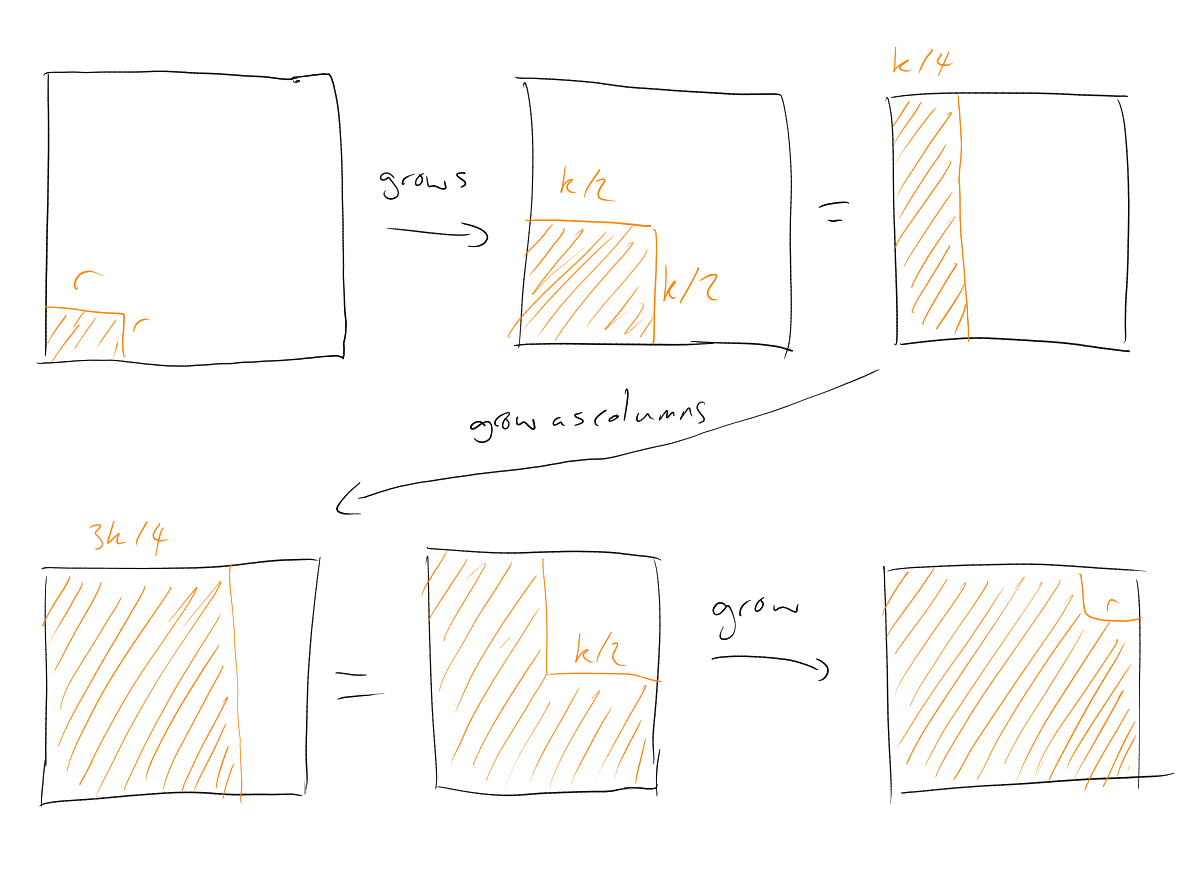
So we have “phase transitions” at and – extremal sets are not nested. This seems to rule out all our compression methods.
And in ?
So in , up to , we get of these phase transitions!
Note that if . Then .
“Some set of the form is best.”
Called the “edge-isoperimetric inequality in the grid”.
The following discussion is non-examinable (until told otherwise).
Proof (sketch). Induction on . is trivial.
Given with , where :
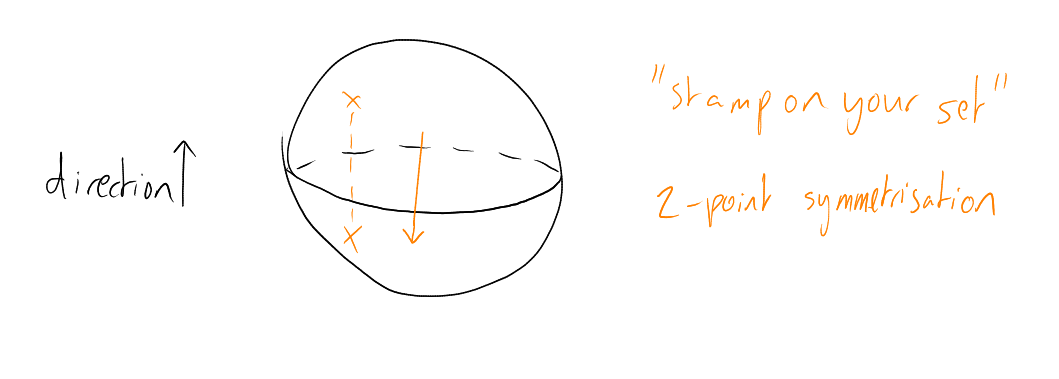
Wlog is a down-set (just down-compress, i.e. stamp on your set in direction for each ). For any , define by giving its -sections:
which will be a set of the form , or a complement. Write . Do we have ?
Now, is a down-set, so
and
The is because not a down-set, as extremal sets in dimension are not nested.
Indeed, can have :
Idea: try to introduce a “fake” boundary : want , with on extremal sets, such that does decrease (then done).
Try . Then for all , equality for extremal sets (as equality for any down-set) and . But: fails for for all .
Could try to fix this by defining . Also fails – for example if is the “outer shell” of then .
So far, have
where is the extremal function in .
Now, is the pointwise minimum of some functions of the form and – each of which is a concave function. Hence itself is a concave function.
Consider varying , keeping constant and keeping .
We obtain , where for some ,
So:
but is still not a down-set.
Now vary, , keeping fixed ( fixed) and .
This is a concave function of – as concave + concave + linear. Hence “make as small or large as possible”.
i.e. , where one of the following holds:
for all
for all , for all
for all , for all .
But (miraculously), this is a down-set!
Hence
So our “compression in direction ” is: .
Now finish as before. □
Remark. To make this precise, work instead in (and then take a discrete approximation at the end).
End of non-examinable discussion.
Remark. Very few isoperimetric inequalities are known (even approximately).
For example, “isoperimetric in a layer” – in the graph , with joined if (i.e. in ).
This is open. Nicest special case is , where it is conjectured that balls are best – i.e. sets of the form .
is called -intersecting if for all .
How large can a -intersecting family be?
Example. . Could take – has size . Or – has size .
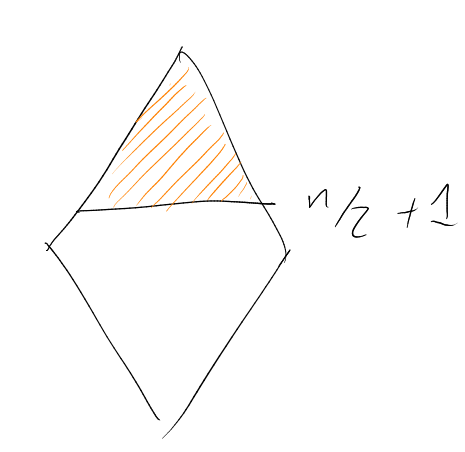
Proof. For any : have , so . So, writing for , have – i.e. disjoint from . Suppose that .
Then, by Harper’s Theorem, we have
But disjoint from , which has size contradicting . □
What about -intersecting ?
Might guess: best is .
Could also try , for .
Example. For -intersecting in:
: , , .
: , , .
: , , .
Note that grows quadratically, linearly, and constant – so largest of these for large.
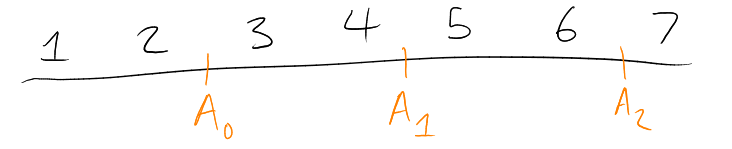
Remark.
Idea of proof: “ has degrees of freedom”.
Proof. Extending to a maximal -intersecting family, we must have some with (if not, then by maximality have that , , , have – whence , contradiction).
May assume that there exists with – otherwise all have . Whence .
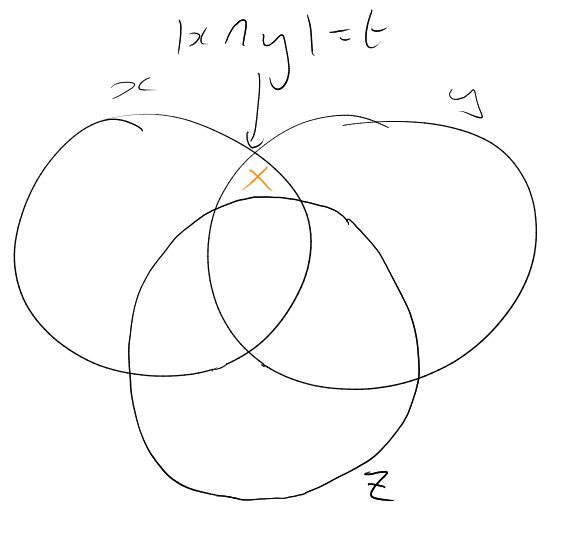
So each must meet in points. Thus
Note that the right hand side is a polynomial of degree – so eventually beaten by . □
For intersecting families, we ban .
What if we banned ?
Example. Want with odd for all distinct ?
Try odd: can achieve , by picture.
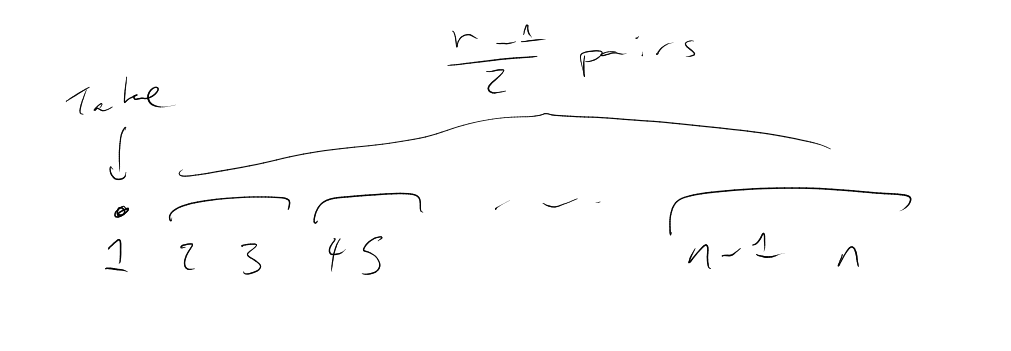
What if, still for odd, had even for all distinct ? Can achieve , by picture.
This is only linear in . Can we improve this?
Similarly if even: For even for all , can achieve – picture
But for odd for all (distinct): can achieve (as above). Can we improve this?
Seems to be that banning forces the family to be very small (polynomial in , in fact a linear polynomial).
Remarkably, cannot beat linear.
Idea: Find linearly independent vectors in a vector space of dimension , namely .
Proof. View as , the -dimensional space over (the field of order ). By identifying with , its characteristic sequence (e.g. for ).
We have for each , as is odd ( is the usual dot-product).
Also, for distinct (as even).
Hence the , are linearly independent (if , dot with to get ). □
Remark. Hence also if , even, with odd for all distinct , then – just add to each and apply Proposition 3 with .
Does this modulo behaviour generalise?
Now show: allowed values for modulo implies polynomial of degree .
Remark.
Idea: Try to find linearly independent points in a vector space of dimension , by somehow “applying the polynomial to ”.
Proof. For each , let be the matrix, with rows indexed by , columns indexed by , with
for each , .
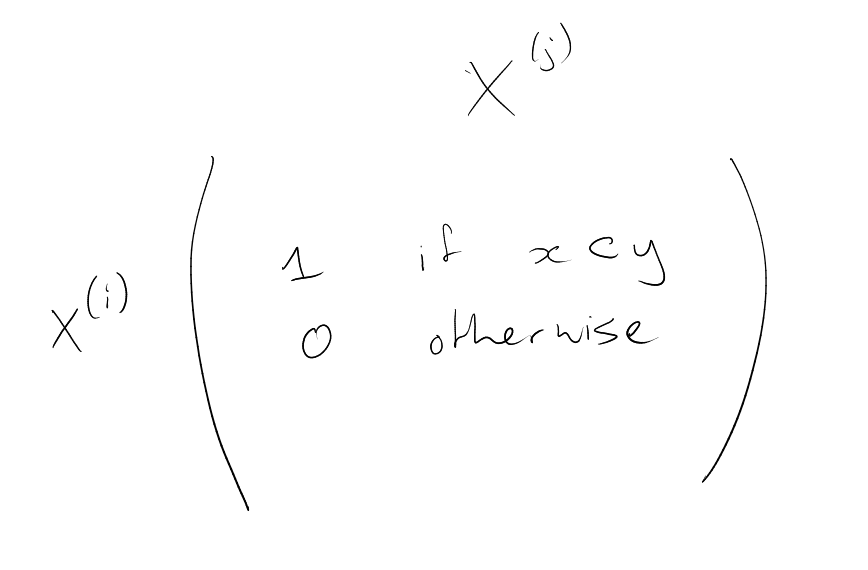
Let be the vector space (over ) spanned by the rows of . So .
For , consider (note each row belongs to , as we premultiplied by a matrix). For , :
So
so all rows of belong to .
Let (note each row is in ).
For , have
Write the integer polynomial as , with – possible because .
Let (each row is in ).
Then for all :
So the submatrix of spanned by the rows and columns corresponding to the elements of is
Hence the rows of corresponding to are linearly independent over , so also over , so also over , so also over .
So . □
Remark. Do need prime. Grolmusz constructed, for each , a value of and a family such that for all distinct we have with . This is not a polynomial in .
Proof. We are allowed values of , so done by Frankl-Wilson Theorem. □
Two -sets in typically meet in about points – but exactly equaling is very unlikely. But remarkably:
Note. is a tiny (exponentially small) proportion of . Indeed, (for some ) whereas .
Proof. Halving if necessary, may assume that no (any ).
Then distinct implies , so .
So by Corollary 5. □
Let be a bounded subset of .
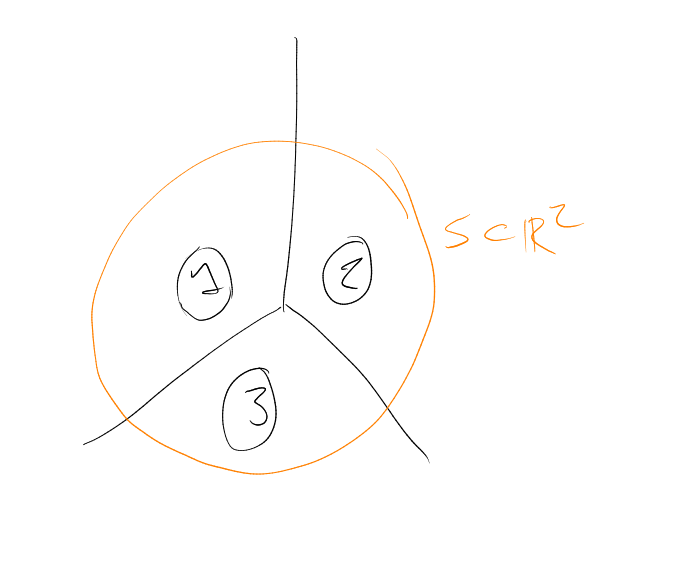
How few pieces can we break into such that each piece has smaller diameter than that of ?
The example of a regular simplex in ( points, all at distance ) shows that we may need pieces.

Conjecture (Borsuk’s conjecture (1920s)). pieces always sufficient.
Known for . Also known for a smooth convex body in or a symmetric convex body in (convex means implies ).
However, Borsuk is massively false:
Note.
Proof. We’ll find – in fact for some . We have already had two genuine ideas from this sentence: first that we think about having , and second that we go for .
Have , so :
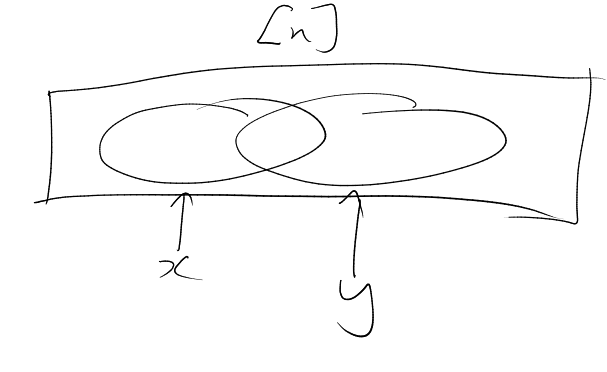
So seek with diameter , but every subset of with is very small (hence we will need many pieces).
Identify with the edge-set of , the complete graph on points.
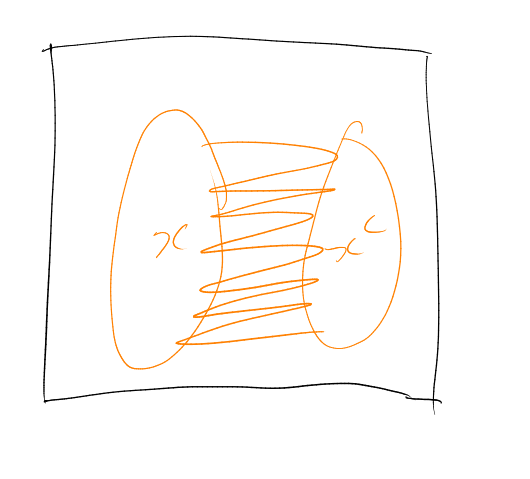
For each let be the complete bipartite graph, with vertex classes . Let . So , and .
Now
where .
This is minimised when , i.e. when .
Now let have smaller diameter than that of : say . So must have distinct: (else diameter of is the diameter of ).
Thus
Conclusion: the number of pieces needed is (for some ). This is , for some , which is at least for some . □
˙