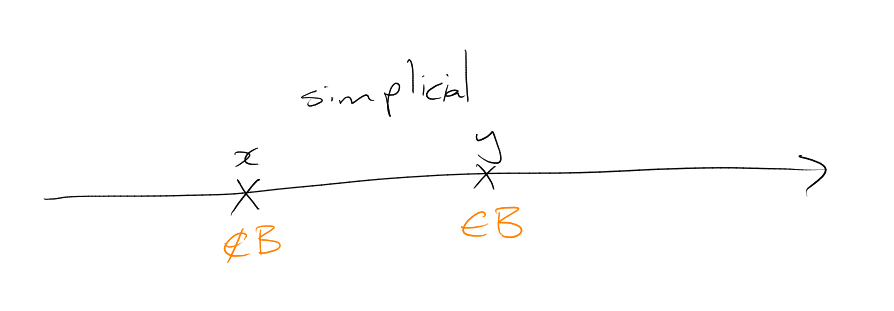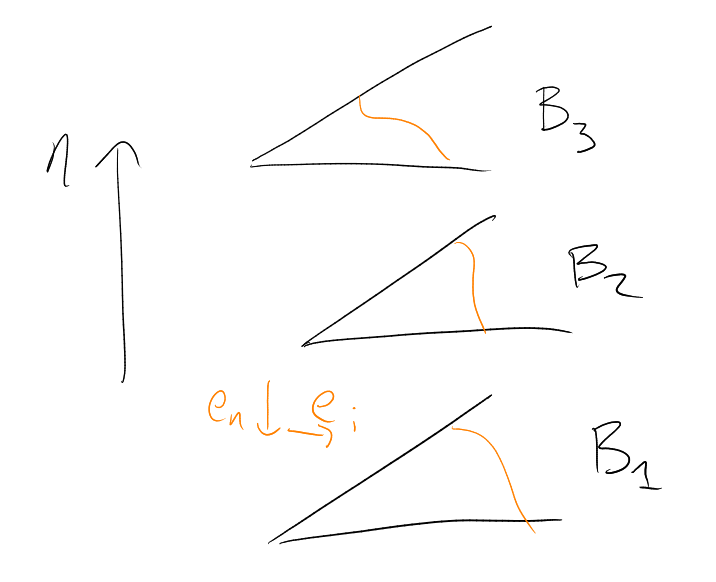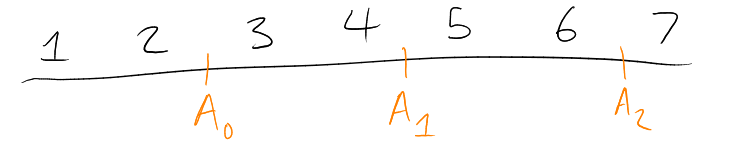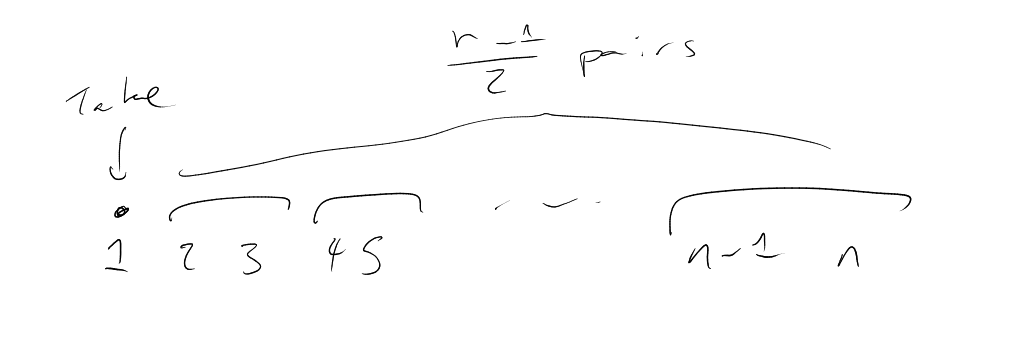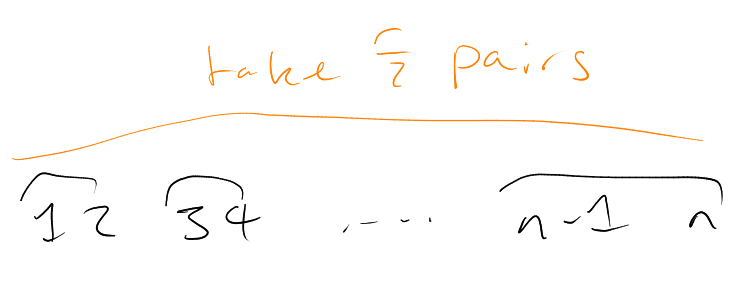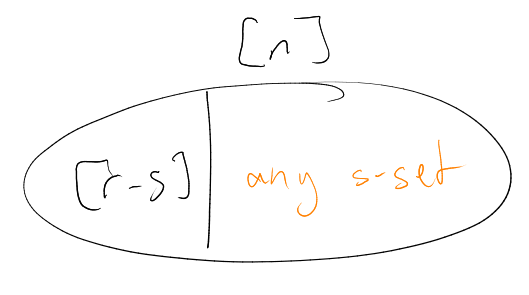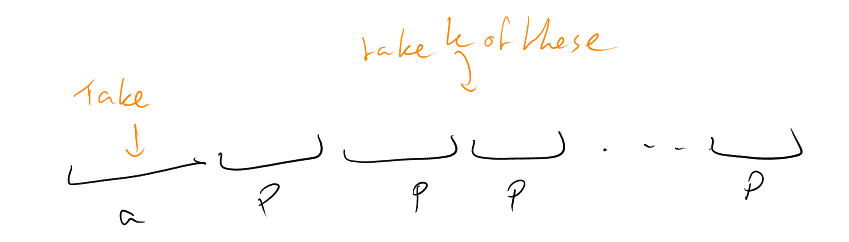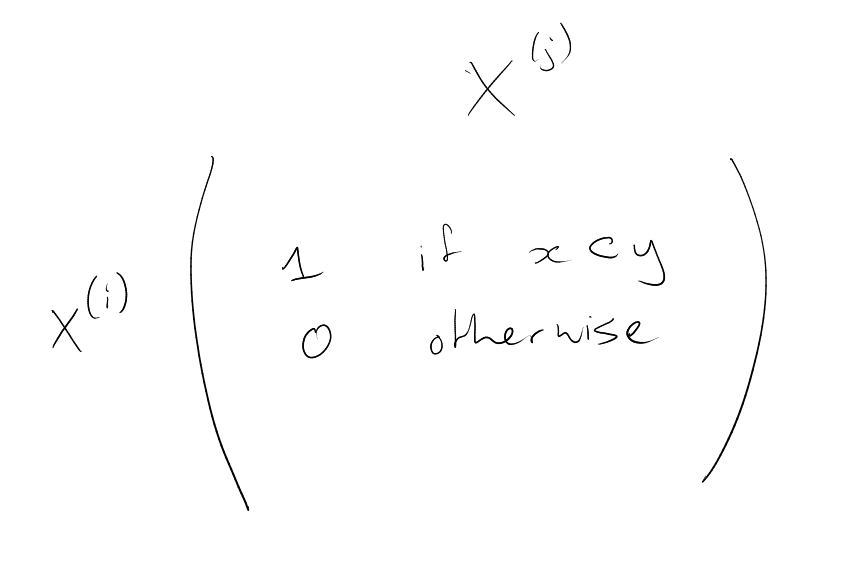Combinatorics
Lectured by Imre Leader
Contents
1 Set Systems
Definition 1 (Set system).
Let
be a set. A set system on
(or a family of subsets of )
is a family .
Notation.
We will use the notation
We call an element of
an -set. We will
usually be using ,
so .
Example.
|
|
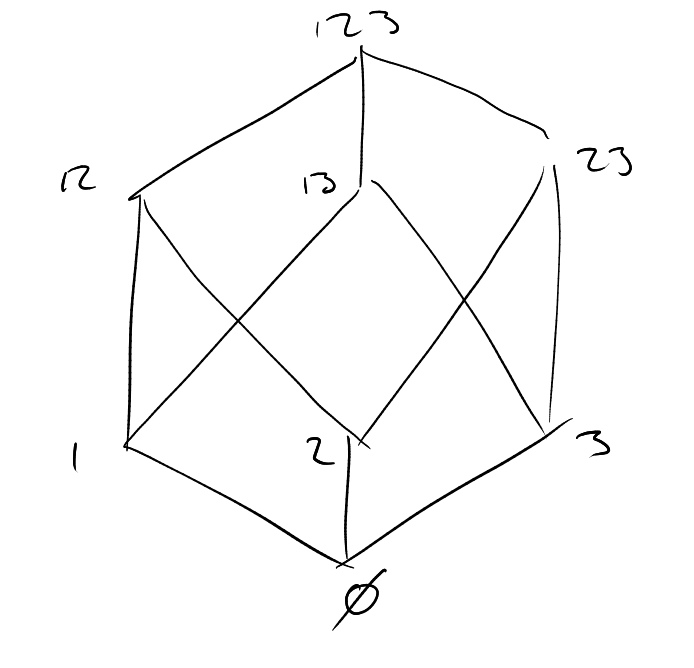
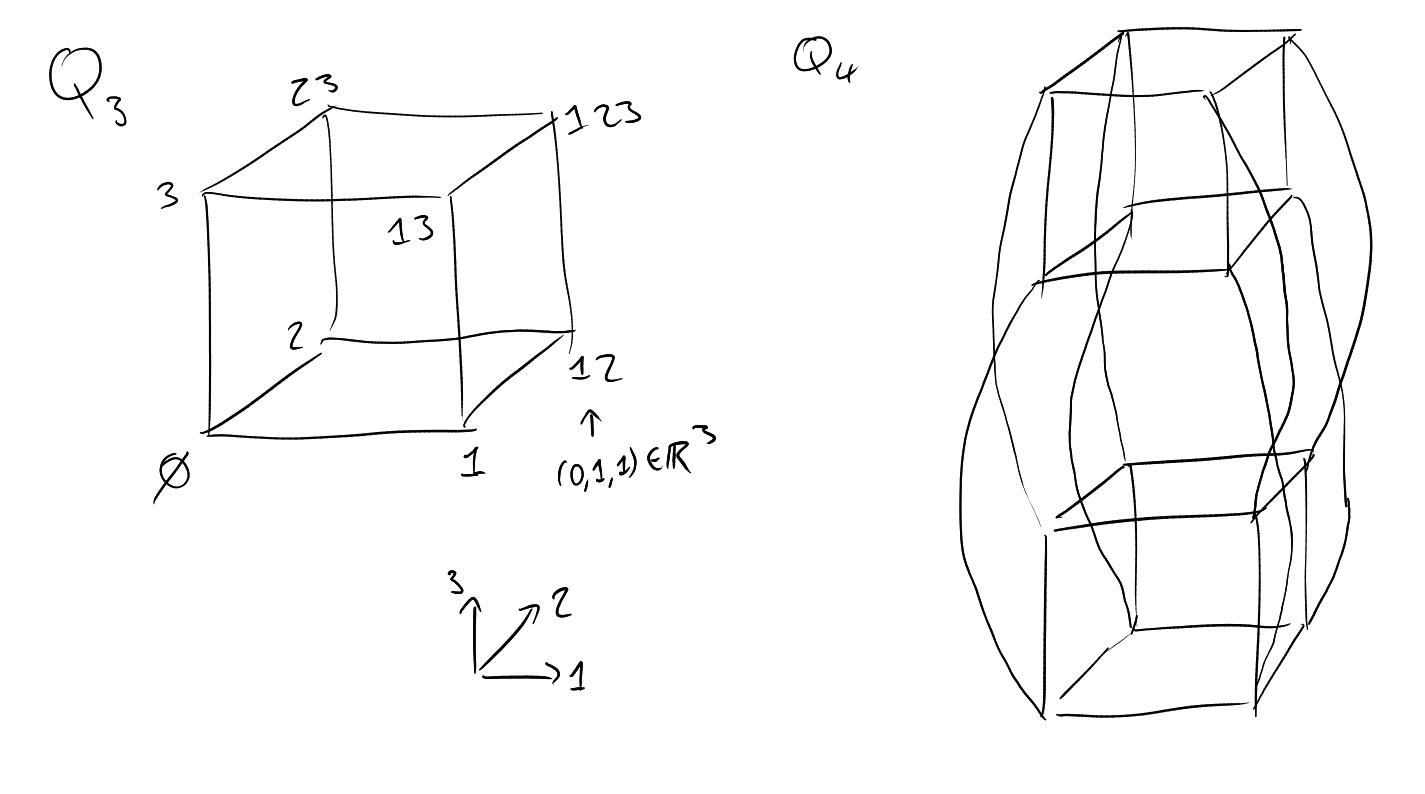
Definition 2 (Discrete cube).
Make
into a graph by joining
and
if ,
i.e. if
for some ,
or vice versa. We call this ths discrete cube
(if ).
Alternatively, can view
as an -dimensional
unit cube , by
identifying e.g.
with (i.e.
identify with
𝟙, the characteristic
function of ).
Definition 3 (Chain).
Say
is a chain if ,
either
or .
Example.
For example,
is a chain.
Definition 4 (Antichain).
Say
is an antichain if ,
,
we have .
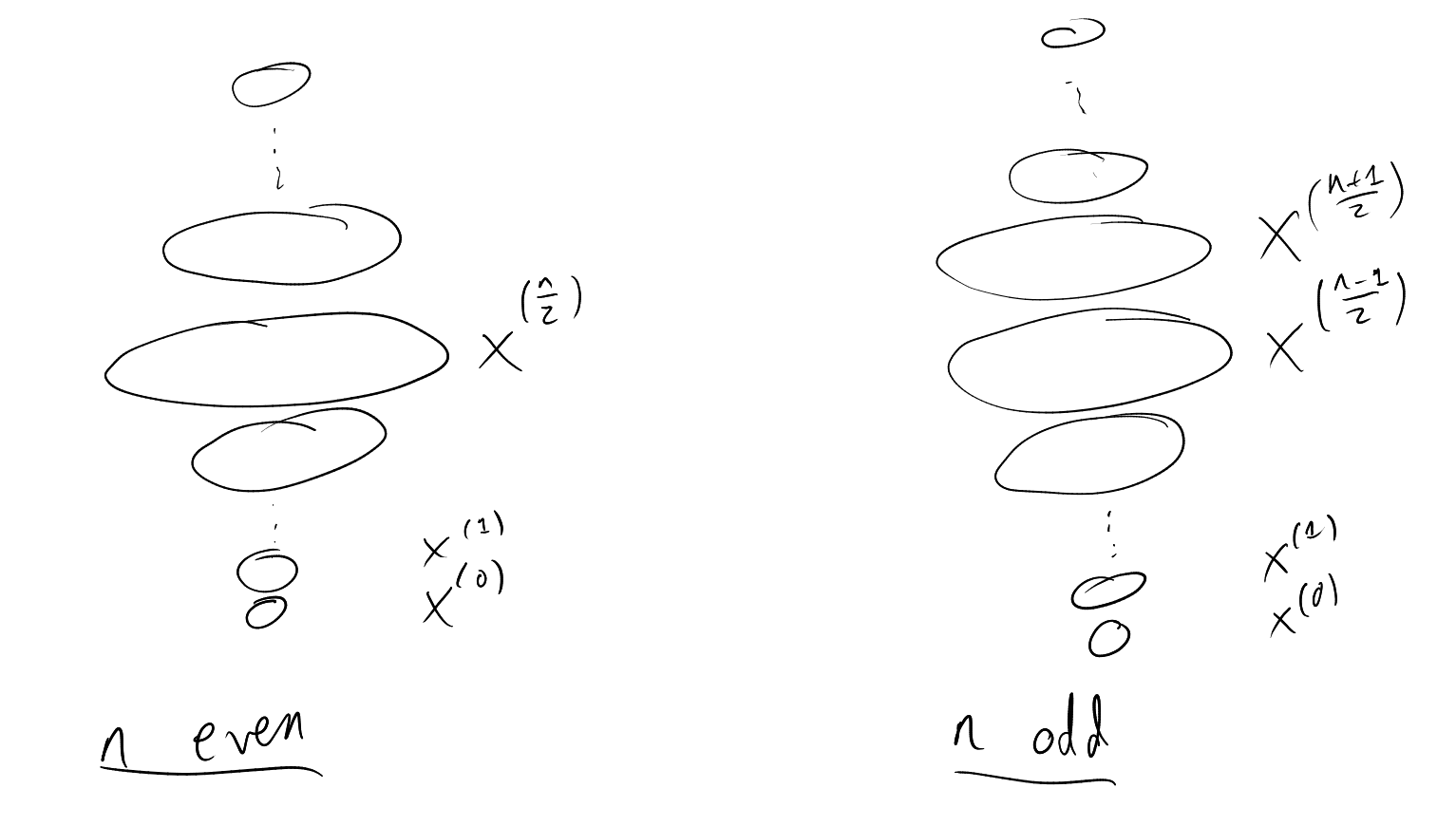
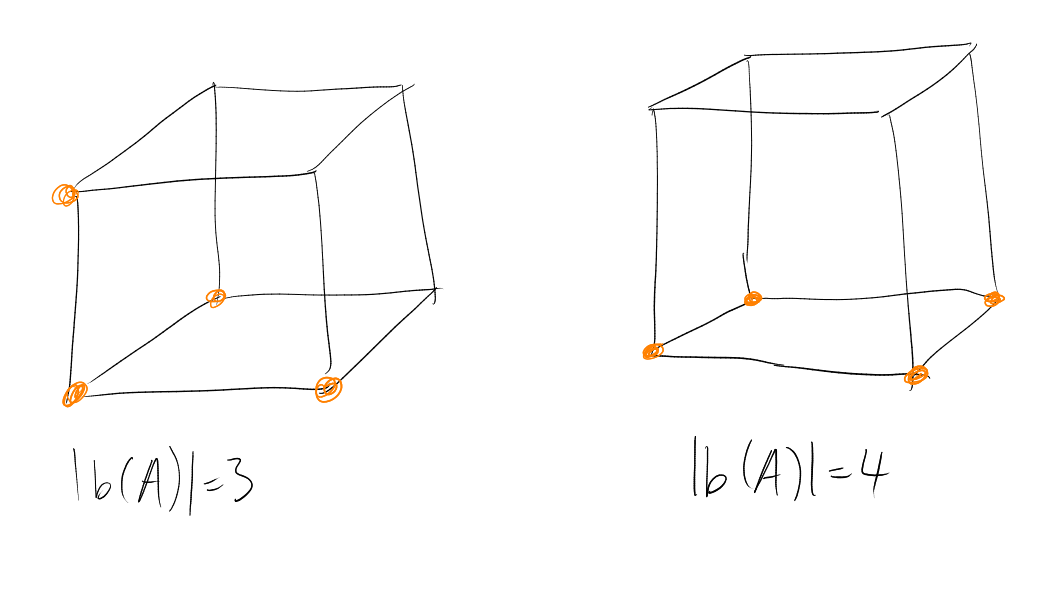
How large can a chain be? Can achieve ,
for example using
Cannot beat this: for each ,
contains
-set.
How large can an antichain be? Can achieve ,
for example . More
generally, can take ,
for any – best
out of these is .
Can we beat this?
Theorem 5 (Sperner’s Lemma).
Assuming that:
Then .
Idea: Motivated by “a chain meets each layer in
point, because a layer is an antichain”, we will try to decompose the cube into chains.
Proof.
We’ll decompose
into
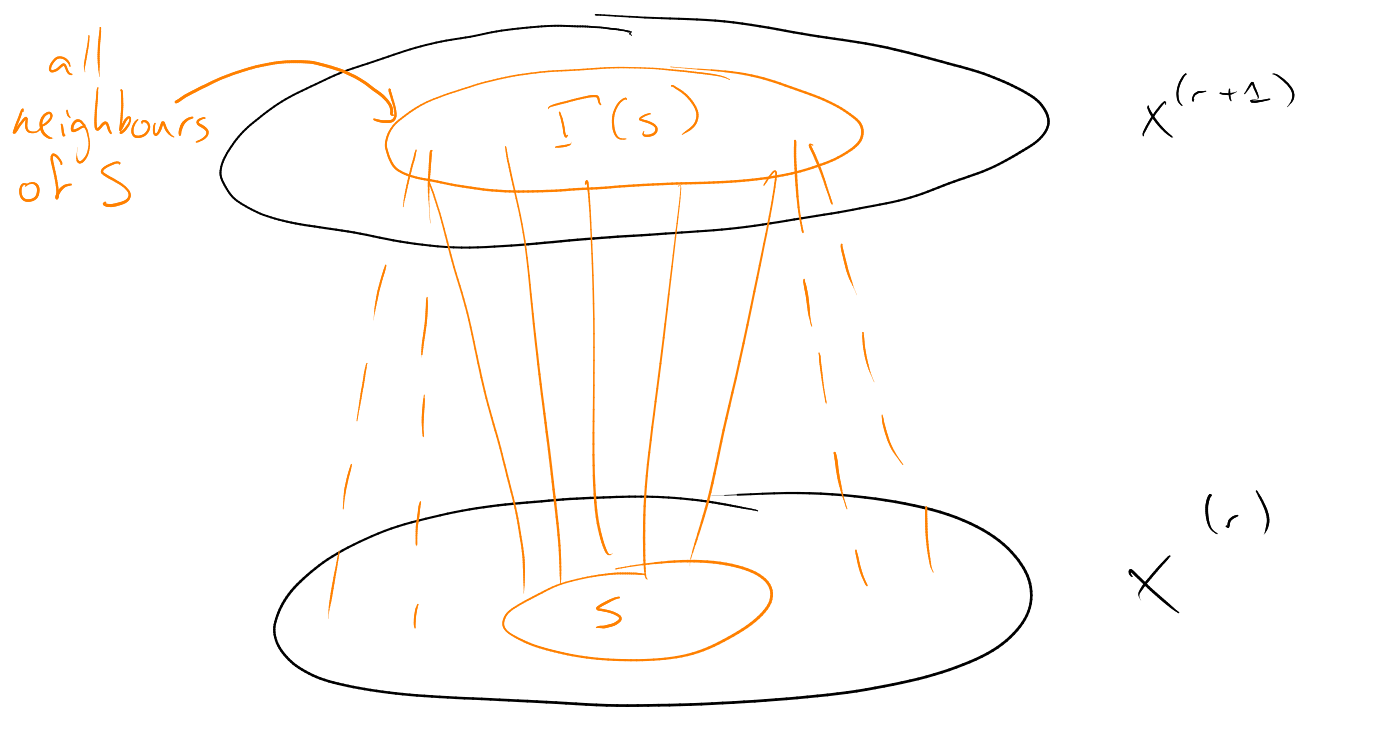
chains – then done. To achieve this, it is sufficient to find:
-
(i)
For each ,
a matching from
to
(recall that a matching here means a set of disjoint edges, one for each point in ).
-
(ii)
For each ,
a matching from
to .
We then put these together to form our chains, each passing through
.
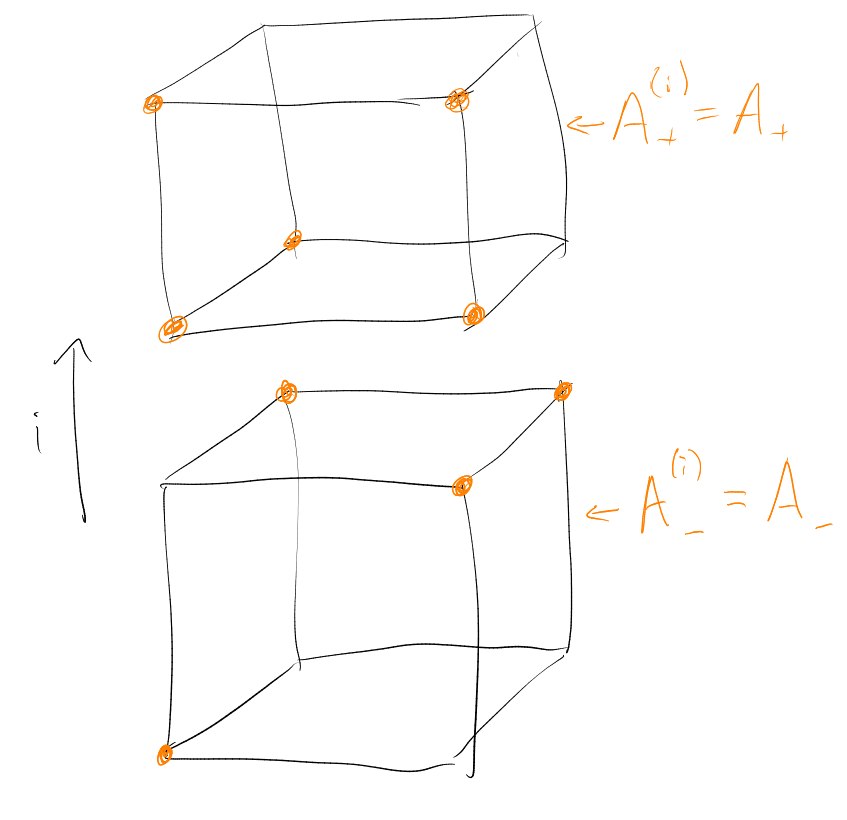
By taking complements, it is enough to prove (i).
Let be the (bipartite)
subgraph of spanned
by : we seek a
matching from
to . For any
, the
number of
edges in is
(counting from
below) and
(counting from above).
Hence, as ,
Thus by Hall’s Marriage theorem, there exists a matching. □
Equality in Sperner’s Lemma? Proof above tells us nothing.
Aim: If
is an antichain then
“The percentages of each layer occupied add up to
.”
Trivially implies Sperner’s Lemma (think about it).
Definition 6 (Shadow).
For
(),
the shadow of
is
defined by, .
Example.
If ,
then .
Proposition 7 (Local LYM).
Assuming that:
“The fraction of the level occupied by
is the fraction
for ”.
Remark.
LYM = Lubell, Meshalkin, Yamamoto.
Proof.
The number of
edges in is
(counting from
above) and is
(counting from above). So
But ,
so done. □
Equality in Local LYM? Must have that ,
,
have
. So
or
.
Theorem 8 (LYM Inequality).
Assuming that:
Notation.
We will now start writing
for .
Proof 1.
“Bubble down with Local LYM”.
Have . Now,
and
disjoint
(as is
an antichain), so
|
|
whence
by Local LYM.
Now, note is
disjoint from
(since is
an antichain), so
|
|
whence
|
|
(Local LYM) so
|
|
Continue inductively. □
Equality in LYM Inequality? Must have had equality in each use of Local LYM. Hence equality in LYM Inequality
needs: max
with
has .
So: equality in Local LYM
for
some .
Hence: equality in Sperner’s Lemma if and only if
(if even),
and or
.
Proof 2.
Choose, uniformly at random, a maximal chain
(i.e.
, with
for all
).
For any -set
,
(all
-sets are equally
likely). So
(as events are disjoint) and hence
|
|
Equivalently: (if you want to lose the intuition about how this works) then:
, and
, hence
1.1 Shadows
For , know
. Equality is
rare – only for
or .
What happens in between?
In other words, given ,
how should we choose
to minimise ?
Believable that if
then we sholud take .
What if ?
Believable that should take
plus some -sets
in . For
example, for
with ,
take .
1.2 Two total orders on
Let and
be distinct
-sets:
say ,
where
and
.
Say that in the lexicographic
(or lex) ordering if for some
we have
for and
.
Slogan: “Use small elements” (“dictionary order”).
Example.
lexicographic on :
.
lexicographic on :
,
.
Say that in the colexicographic
(or colex) ordering if for some
we have
for all
and .
Slogan: “Avoid large elements” (note that this is not quite the same as “use small elements”, which is what we
had before).
Example.
colexicographic on :
.
colexicographic on :
,
.
Note that, in colexicographic,
is an initial segment (first
elements, for some )
of .
This is false for lex.
So we could view colexicographic as an enumeration of
.
Aim: colexicographic initial segments are best for
, i.e. if
and
is the initial segment
of colexicographic with ,
then .
In particular, .
1.3 Compressions
Idea: try to transform
into some
such that:
-
(i)
.
-
(ii)
.
-
(iii)
looks more like’
than
did.
Ideally, we’d like a family of such ‘compressions’:
such that either
or is so similar to
that we can directly
check that .
“colexicographic prefers 1 to 2” inspires:
Definition 9 (-compression).
Fix .
The -compression
is defined as follows:
For , set
|
|
and for ,
set
|
|
Note that the second part of the union in is
because we need to make sure that we “replace
by
where possible”.
Example.
If
then .
So , and
.
Say is
-compressed
if .
Proof.
Write
for . Let
. We’ll show
that ,
and
. [Then
done].
Have for
some ,
with
(as ). So
,
, and
.
Cannot have ,
else ,
giving ,
contradiction.
Hence we have ,
.
Also, ,
since .
Suppose : so
for some
. Cannot
have ,
else –
so (as
),
contradicting .
Hence
and .
Whence both
and belong
to (by
definition of ),
contradicting .
□
Remark.
Actually showed that .
Definition 11 (Left-compressed).
Say
is left-compressed if
for all .
Corollary 12.
Assuming that:
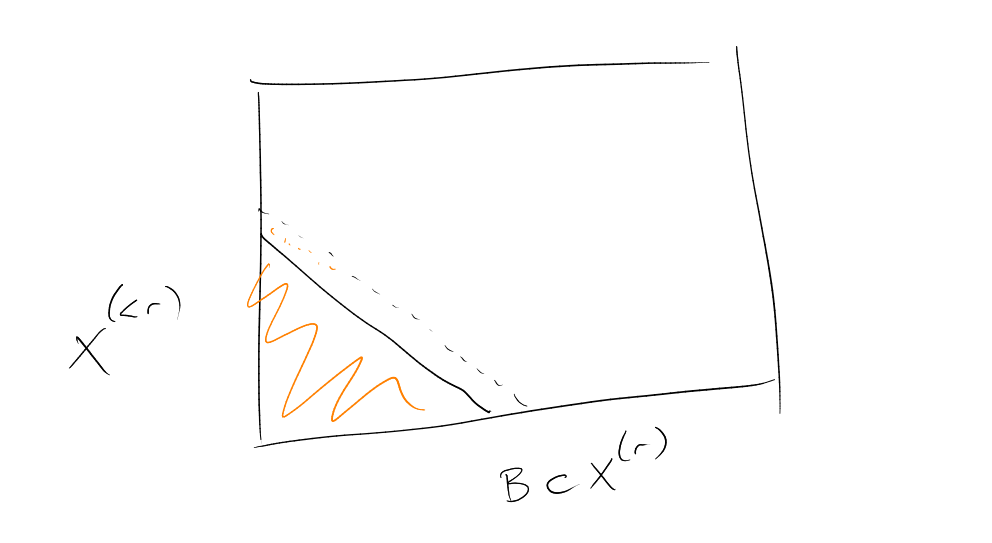
Proof.
Define a sequence
as follows. Set .
Having defined ,
if
left-compressed then stop the sequence with .
If not, choose
such that
is not -compression,
and set .
This must terminate, because for example
is strictly decreasing in .
Final term
satisfies ,
and
(by Lemma 10) □
Remark.
-
(1)
Or: among all
with
and ,
choose one with minimal .
-
(2)
Can choose order of the
so that no
applied twice.
-
(3)
Any initial segment of colexicographic is left-compressed. Converse false, for example
(initial segment of lexicographic).
These compressions only encode the idea “colexicographic prefers
to
()”, but
this is also true for lexicographic.
So we try to come up with more compressions that encode more of what colexicographic likes.
“colexicographic prefers
to ”
inspires:
Definition 13 (-compression).
Let
with ,
and
. We define the
-compression as
follows: for ,
|
|
and for ,
set
|
|
Example.
If
|
|
then
|
|
So , and
.
Say is
-compressed
if .
Sadly, we can have :
Example.
has ,
but has
.
Despite this, we at least we do have the following:
Proof.
Suppose not. So there exists
with , in
colexicographic but ,
.
Put ,
.
Then , and
disjoint,
and
(since ,
by definition of colexicographic).
So ,
contradicting is
-compression.
□
Lemma 15.
Assuming that:
-
-
-
-
-
-
|
|
Proof.
Let .
For , we’ll
show ,
, and
. (Then
done).
Have for
some ,
and , so
,
, and
(by definition
of ).
If : there
exists such
that is
-compressed,
so from we
have –
contradicting ,
contradiction.
Thus ,
and so ,
. Certainly
(because
), so just need
to show that .
Suppose : so
, for some
. Also have
(for
example, as
contained in it).
If :
know is
-compressed
for some , so
–
contradicting .
If : have
,
, so by definition
of we must have
that both
and –
contradicting ,
a contradiction. □
Theorem 16 (Kruskal-Katona).
Assuming that:
Then . In
particular: if
,
then
.
Proof.
Let . Define
a sequence of
set systems in
as follows:
-
Set .
-
Having chosen ,
if
is -compressed
for all
then stop. Otherwise, choose
with
minimal such that
is not -compressed.
Note that
such that
(namely, use ).
So ()
is satisfied.
So Lemma 15 tells us that .
Set ,
and continue.
Must terminate, as is strictly
decreasing. The final term
satisfies ,
and is
-compressed
for all .
So by
Lemma 14. □
For ,
, the upper
shadow of
is
|
|
Corollary 17.
Assuming that:
Note that the shadow of an initial segment of colexicographic on
is an initial segment
of colexicographic on
– as if
then .
This fact gives:
Corollary 18.
Assuming that:
-
,
and
is the initial segment of
colexicographic on
with
Then
for all
.
Proof.
If ,
then ,
because
is an initial segment of colexicographic. Done by induction. □
Note.
If ,
then .
1.4 Intersecting Families
Say
intersecting if
for all .
How large can an intersecting family be? Can have
, by
taking .
Proposition 19.
Assuming that:
Then .
Proof.
For any ,
at most one of
can belong to .
□
Note.
Many other extremal examples. For example, for
odd
take .
What if ?
If , take
.
If : just choose
one of
for all :
gives .
So interesting case is .
Could try .
Has size
(while this identity can be verified by writing out factorials, a more useful way of observing it is by noting
that ).
Could also try .
Example.
,
. Then
and
|
|
Theorem 20 (Erdos-Ko-Rado Theorem).
Assuming that:
Then .
Proof 1 (“Bubble down with Kruskal-Katona”).
Note that
.
Let . Have
and
are disjoint
families of -sets.
Suppose . Then
. Whence by
Kruskal-Katona we have .
So , a
contradiction. □
Remark.
Calculation at the end had to give the right answer, as the
calculations would
all be exact if .
Proof 2.
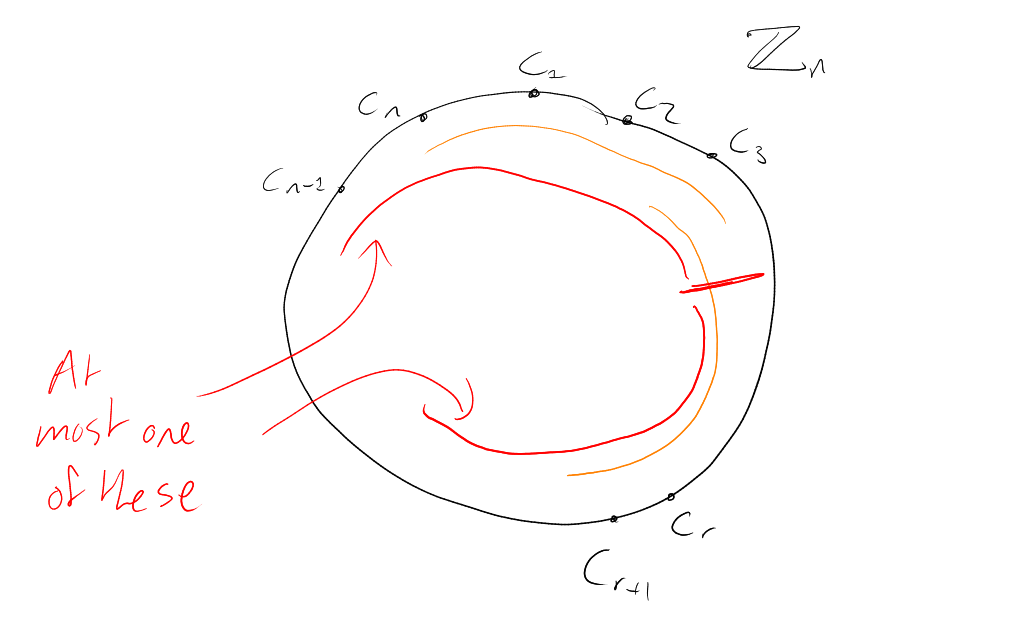
Pick a cyclic ordering of
i.e. a bijection .
How many sets in
are intervals (
consecutive elements) in this ordering?
Answer: . Because
say . Then for each
, at most one of
the two intervals
and can belong
to (subscrpits
are modulo ).
For each -set
, in how
many of the
cyclic orderings is it an interval?
Answer:
( where,
order
inside ,
order
outside ).
Hence ,
i.e. .
□
2 Isoperimetric Inequalities
“How do we minimise the boundary of a set of given size?”
Example.
Among all subsets of
of given area, the disc minimises the perimeter.
Among all subsets of of
given volume, the solid sphere minimises the surface area.
Among all subsets of
of given surface area, the circular arc has the smallest perimeter.
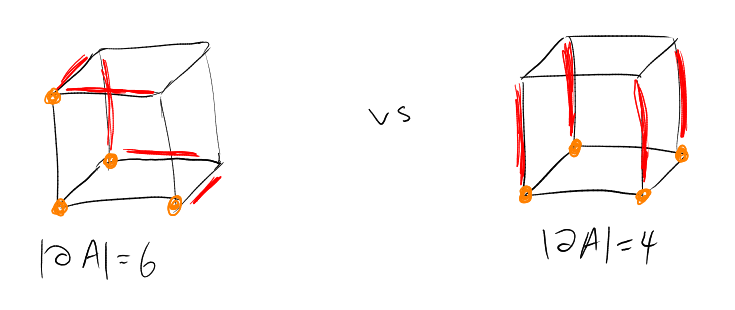
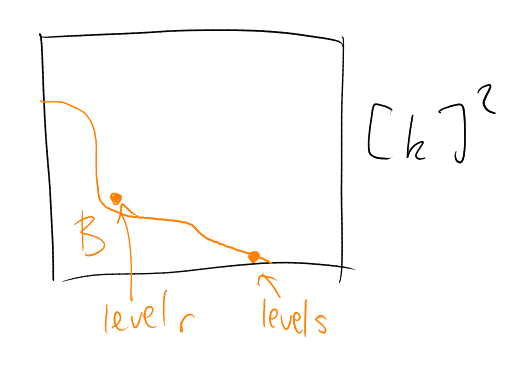
Definition (Boundary in a graph).
For a set
of vertices of a graph ,
the boundary of
is
|
|
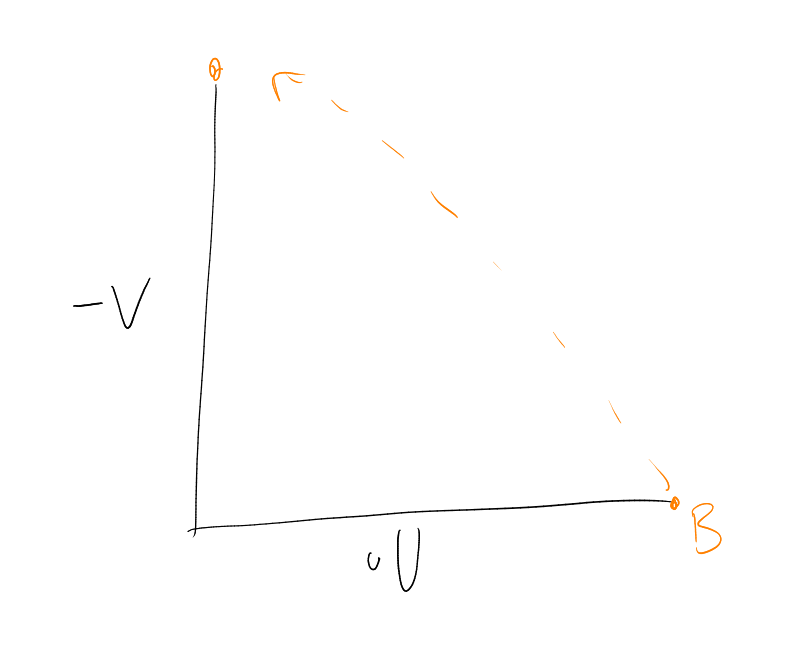
Example.
Here, if ,
then .
Definition (Isoperimetric inequality).
An isoperimetric inequality on
is an
inequality of the form
for some function .
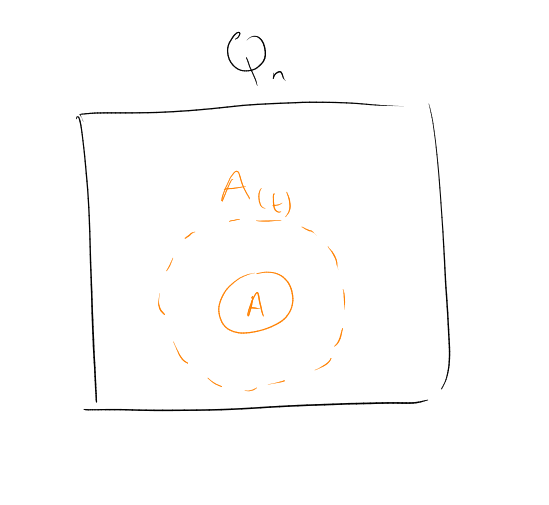
Definition (Neighbourhood).
Often simpler to look at the neighbourhood of
:
. So
A good example for
might be a ball .
What happens for ?
Good guess that balls are best, i.e. sets of the form
.
What if ?
Guess: take
with . If
, where
, then
. So we’d
take to
be an initial segment of lexicographic (by Kruskal-Katona).
This suggests...
In the simplicial ordering on ,
we set
if either
or and
in
lexicographic.
Aim: initial segments of simplicial ordering minimise the boundary.
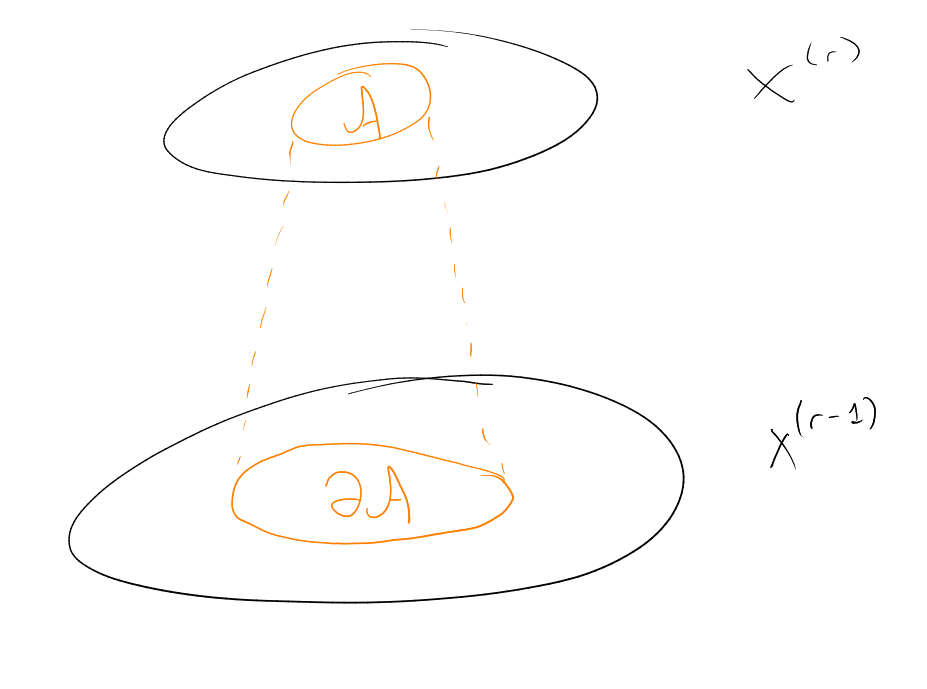
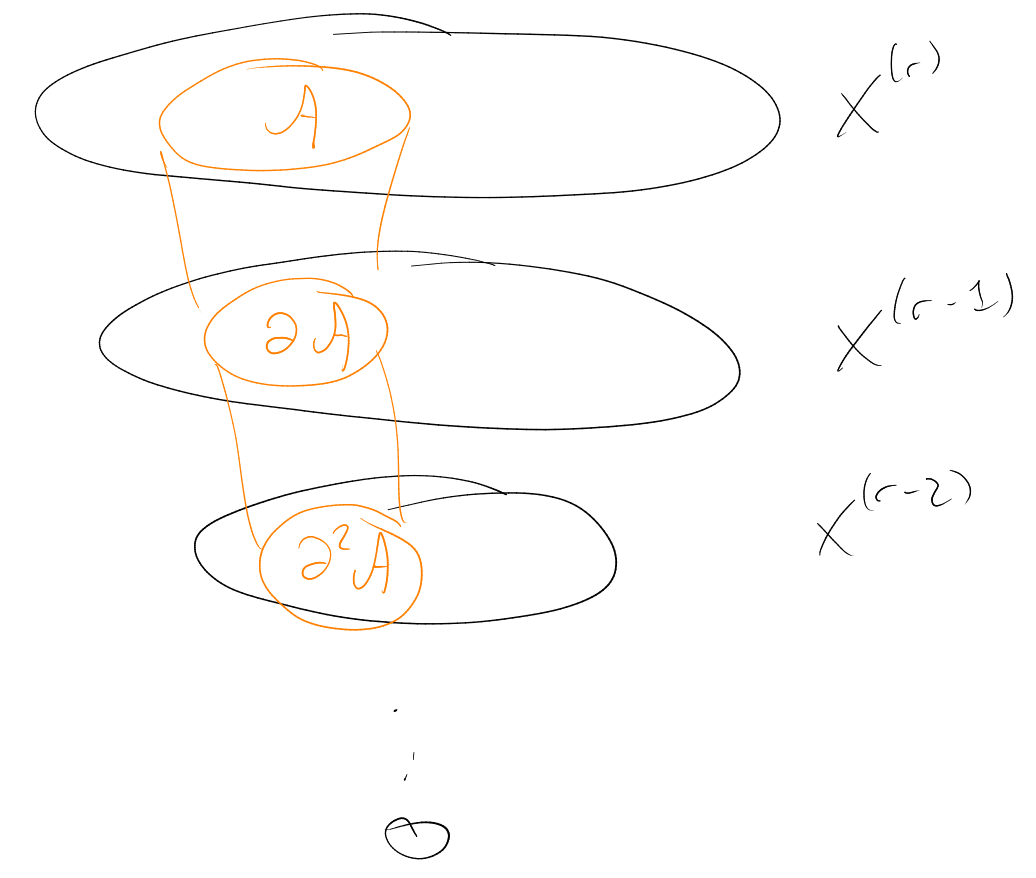
Definition (-sections).
For and
, the
-sections of
are the
families
given by:
The -compression
of in the
family
given by:
Example.
Certainly .
Say is
-compressed
if . Also,
“looks more like” a
Hamming ball than
does.
Here, a Hamming ball is a family
with , for
some .
Theorem 1 (Harper’s Theorem).
Assuming that:
Then . In
particular, if
then
.
Proof.
Induction on :
is
trivial.
Given ,
and ,
and .
Claim: .
Proof of claim: Write
for . We
have
and of course
Now, and
(by the induction hypothesis).
But is an initial segment of
simplicial ordering, and
is an initial segment of simplicial ordering (as neighbourhood of initial segment is an initial segment).
So then and
are nested (one conatined
in the other). Hence .
Similarly, .
Hence ,
which completes the proof of our claim. □
Define a sequence
as follows:
Must terminate, because
is strictly decresing.
The final family
satisfies ,
, and is
-compressed
for all .
Does
-compressed for
all imply that
is an initial segment of
simplicial ordering? (If yes, then
and we are done).
Sadly, no. For example in
can take :
However:
Lemma 2.
Assuming that:
Then one of the following is true:
-
either
is odd, say ,
and
-
or
is even, say ,
and .
For the even case: “Remove the last -set
with , and add
the first -set
without .”
After we prove this, we will have solved our problem, as in each case we certainly have
.
Proof.
Since
is not an initial segment of simplicial ordering, there exists
(in simplicial
ordering) with ,
.
For each :
cannot have ,
(as
is
-compressed). Also
cannot have ,
for the
same reason.
So .
Thus: for each , there
exists at most one earlier
with (namely
). Similarly,
for each there is
at most one later
with
(namely ).
So , with
the
predessor of
and .
Hence if
then is the
last -set,
and if then
is the
last -set
with .
□
Proof of Theorem 1.
Done by above. □
For and
, the
-neighbourhood
of is
.
Corollary 3.
Assuming that:
Proof.
Theorem 1 with induction on .
□
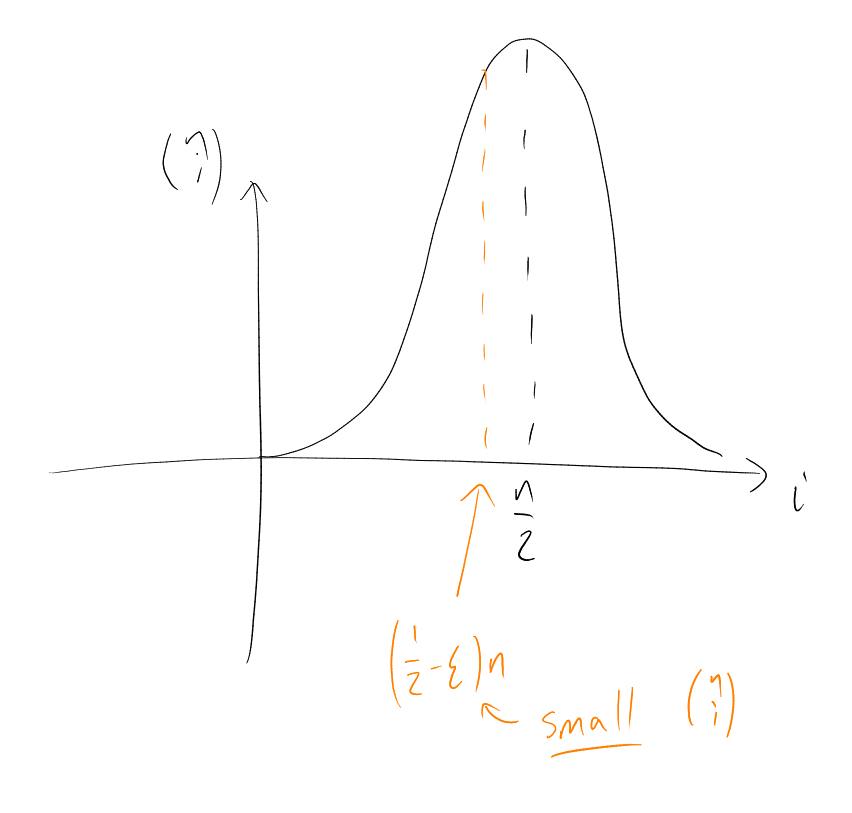
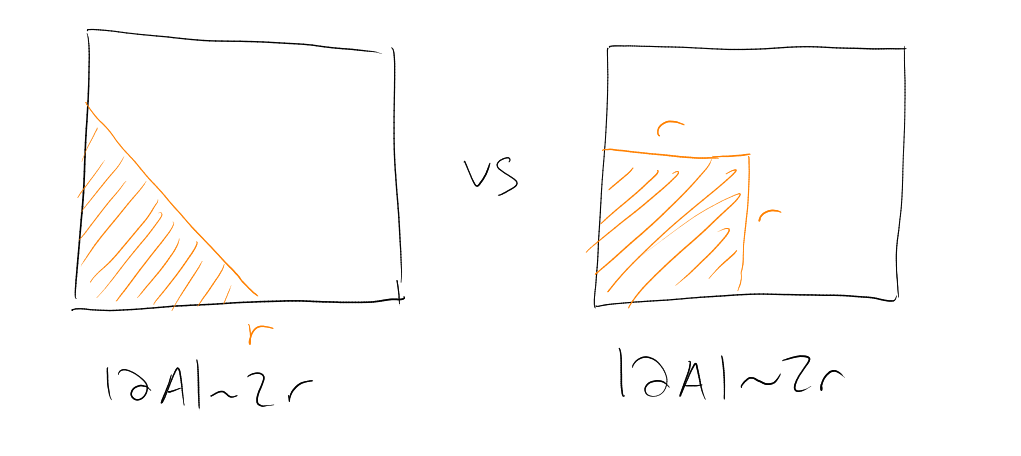
To get a feeling for the strength of Corollary 3, we’ll need some estimates on things like
.
“Going standard deviations
away from the mean .”
Proposition 4.
Assuming that:
Then |
|
“For fixed,
, this is an exponentially
small fraction of .”
Proof.
For :
so
|
|
Hence
|
|
(sum of a geometric progression).
Same argument tells us that
Thus
|
|
Theorem 5.
Assuming that:
Then .
“-sized sets have exponentially
large -neighbourhoods.”
Proof.
Enough to show that if
an integer then
Have , so by Harper’s
Theorem, we have ,
so
|
|
Remark.
Same would show, for “small” sets:
|
|
2.1 Concentration of measure
Say is
Lipschitz if
for all
adjacent.
For , say
is a Lévy mean
or median of
if
and
Now ready to show “every well-behaved function on the cube
is
roughly constant nearly everywhere”.
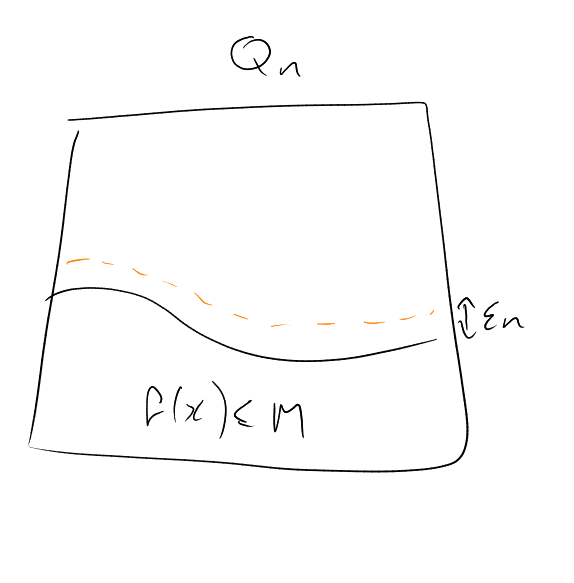
Theorem 6.
Assuming that:
Then |
|
for any .
Note.
This is the “concentration of measure” phenomenon.
Proof.
Let .
Then ,
so
ut is
Lipschitz, so
implies .
Thus
|
|
Similarly,
|
|
Hence
|
|
Let be a graph
of diameter
().
Definition ().
Write
|
|
So
small says “-sized
sets have large -neighbourhoods”.
Definition (Levy family).
Say a sequence of graphs is a Lévy family if
as ,
for each .
So Theorem 5 tells us that the sequence
is a Lévy family – even a normal Lévy family, meaning
grows exponentially
small in , for
each .
So have concentration of measure for any Lévy family.
Many naturally-occurring families of graphs are Lévy families.
Example.
, where
is made into a
graph by joining
to if
is a
transposition.
Can define similarly for
any metric measure space
(of finite measure and finite diameter).
We deduced concentration of measure from an isoperimetric inequality.
Conversely:
Proposition 7.
Assuming that:
-
,
and
are such that for any
Lipschitz function
with
median
we have
Then for all
with
, we
have
.
2.2 Edge-isoperimetric inequalities
For a subset of
vertices of a graph ,
the edge-boundary of
is
An inequality of the form: for
all is an edge-isoperimetric
inequality on .
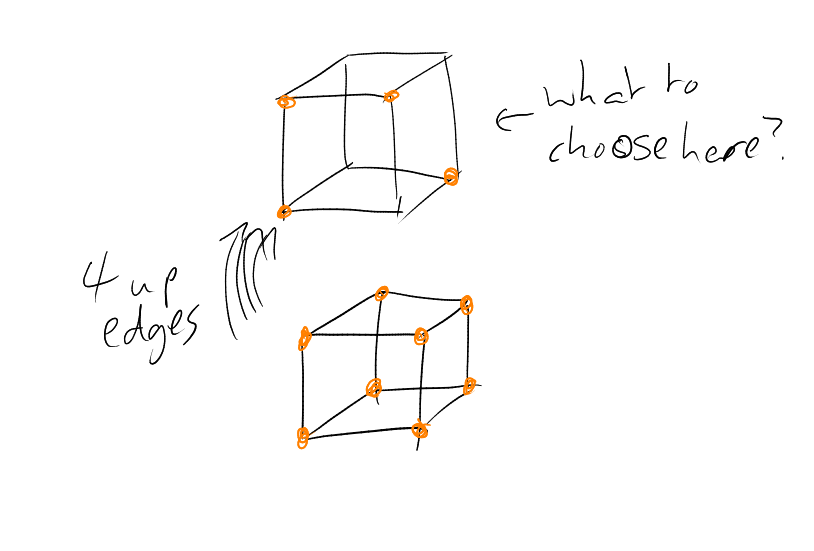
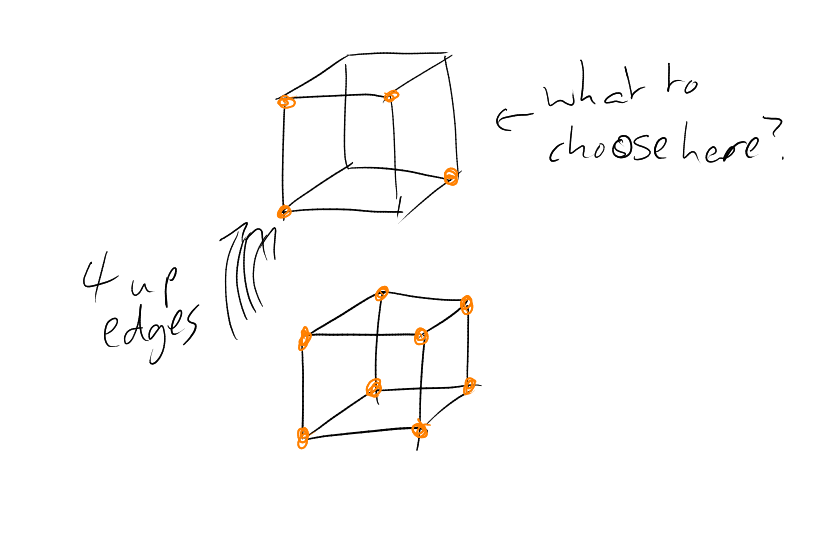
What happens in ?
Given , which
should we take,
to minimise ?
This suggests that maybe subcubes are best.
What if ? with
? Natural to
take . Suppose
we are in , and
considering , eg
. We might take the
whole of the bottom layer, and then stuff in the upper layer. Note that the size of the boundary will be the number of up
edges (which is ,
a constant), plus the number of edges in the top layer. So we just want to minimise the number of edges in the top
layer, i.e. find
with
with minimal boundary.
So we define: for ,
, say
in the binary
ordering on if
. Equivalently,
if and
only if .
“Go up in subcubes”.
Example.
In :
.
For ,
, we define
the -binary
compression by
giving its -sections:
so . Say
is
-binary
compressed if .
Theorem 8 (Edge-isoperimetric inequality in ).
Assuming that:
-
-
let
the initial segment of binary on
with
Then . In
particular: if
then
.
Remark.
Sometimes called the “Theorem of Harper, Lindsey, Bernstein & Hart”.
Proof.
Induction on .
trivial.
For ,
,
:
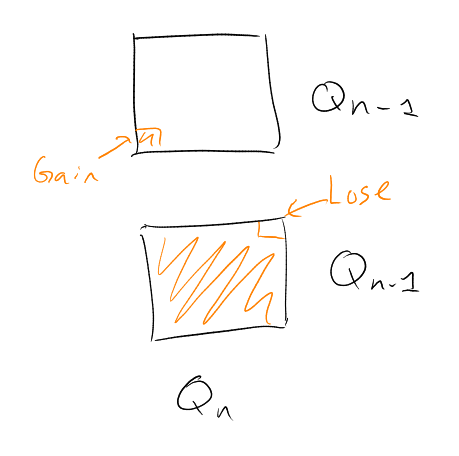
Claim: .
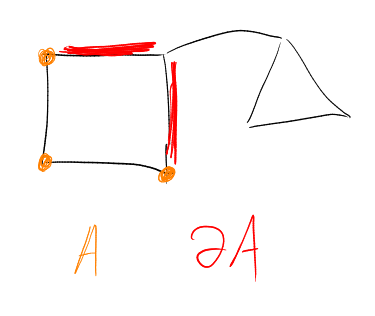
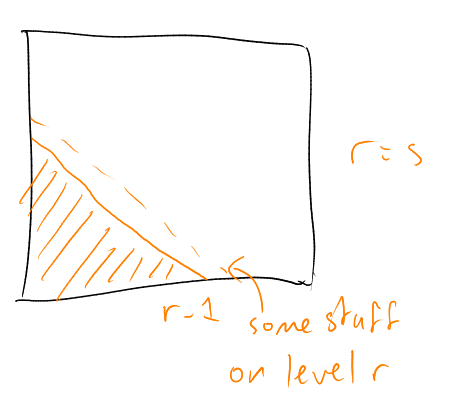
Proof of claim: write
for .
.image Have
Also
|
|
Now, and
(induction hypothesis).
Also, the sets
and
are nested (one is contained inside the other), as each is an initial segment of binary on
.
Whence we certainly have .
So .
Define a sequence
as follows: set .
Having defined ,
if is
-binary compressed
for all then stop
the sequence with .
If not, choose
with and put
. Must terminate,
as the function
is strictly decreasing.
The final family
satisfies ,
, and
is
-binary compressed
for all .
Note that need not be an initial
segment of binary, for example .
However:
Lemma 9.
Assuming that:
Then
(“downstairs minus the last point, plus the first upstairs point”).
(Then done, as clearly ,
since ).
Proof.
As
not an initial segment, there exists
with ,
.
Then for all :
cannot have ,
and cannot have
(as
is -binary
compressed).
Thus for each ,
there exists at most 1 earlier
(namely ).
Also for each
there is at most one later
(namely ).
Then
and
adjacent (since
is the unique element in
after ,
and
is the unique element not in
before ).
So ,
where
is the predecessor of
and .
So must have .
□
This concludes the proof of Theorem 8. □
Remark.
Vital in the proof of Theorem 8, and of Theorem 1, that the extremal sets (in dimension
) were
nested.
The isoperimetric number of a graph
is
|
|
is the “average
out-degree of ”.
Corollary 10.
is 1.
Proof.
Taking ,
we show
(as ).
To show ,
just need to show that if
is an initial segment of binary with
then .
But ,
so certainly .
□
2.3 Inequalities in the grid
For any , the grid
is the graph on
in which is
joined to if
for some we
have for
all and
.
“distance is -distance”.
Note that for
this is exactly .
Do we have analogues of Theorem 1 and Theorem 8 for the grid?
Starting with vertex-isoperimetric: which sets
(of given size) minimise ?
Example.
In :
For :
.
For :
.
This suggests we “go up in levels” according to
– e.g. we’d take .
What if ?
Guess: take plus
some points with ,
but which points?
Example.
In :
so “keep
large”.
This suggests in the simplicial order on ,
we set
if either
or and
, where
.
Example.
On :
,
,
,
,
,
,
,
,
.
On :
,
,
,
,
,
,
,
,
,
,
,
,
…
r
(), and
, the
-sections
of are
the sets
(or ) as
a subset of
defined by:
|
|
for each .
The -compression
of is
is defined by
giving its -sections:
|
|
Thus .
Say is
-compressed
if .
Theorem 11 (Vertex-isoperimetric inequality in the grid).
Assuming that:
Then . In
particular, if
then
.
Proof.
Induction on .
For
it is trivial: if ,
then .
Given
and :
fix .
Claim: .
Proof of claim: write
for . For
any , we
have
|
|
(where ).
Also,
Now, and
, and
(induction hypothesis).
But the sets ,
,
are nested (as each is an initial
segment of simplicial order on ).
Hence for
each .
Thus .
Among all
with and
, pick one that
minimises the quantity .
Then is
-compressed
for all .
Note however, that this time we will make use of this minimality property of
for more than just
deducing that
is -compressed
for all .
Case 1: . What we
know is precisely that
is a down-set ( is
a down-set if ,
)
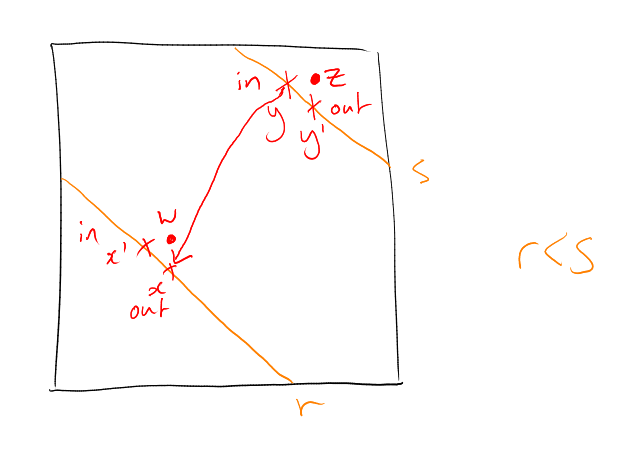
Let and
. May assume
, since
implies
would
imply .
If : then
. So
clearly .
If : cannot
have , because
then also
(as is a
down-set).
So there exists
with ,
,
and
(,
).
Similarly, cannot have ,
because then (as
is a down-set).
So there exists
with ,
,
and
. Now let
. From
we lost
point in the neighbourhood
(namely in the picture), and
gained point (the only point
that we can possibly gain is ),
so . This contradicts
minimality of .
This finishes the two dimensional case.
Case 2: .
For any
and any
with ,
. Have
(as
is
-compressed for any
, so apply with some
). So, considering
the -sections
of , we
have for
all .
Recall that .
So in fact
for all .
Thus
|
|
Similarly,
So to show , enough
to show that
and .
: define a set
as follows:
put , and for
set
. Then
, so
. Also,
is an initial segment of
simplicial order. So in fact ,
whence .
: define
a set as
follows: put
and for
set
( is the biggest it
could be given ).
Then , so
. Also,
is an initial segment of
simplicial order. So ,
whence .
□
Corollary 12.
Assuming that:
Then
for all
.
Remark.
Can check from Corollary 12 that, for
fixed, the sequence
is a Lévy family.
2.4 The edge-isoperimetric inequality in the grid
Which set (of given size)
should we take to minimise ?
Example.
In :
Suggests squares are best.
However...
So we have “phase transitions” at
and –
extremal sets are not nested. This seems to rule out all our compression methods.
And in ?
So in ,
up to ,
we get
of these phase transitions!
Note that if .
Then .
Theorem 13.
Assuming that:
Then |
|
“Some set of the form
is best.”
Called the “edge-isoperimetric inequality in the grid”.
The following discussion is non-examinable (until told otherwise).
Proof (sketch).
Induction on .
is trivial.
Given
with ,
where :
Wlog
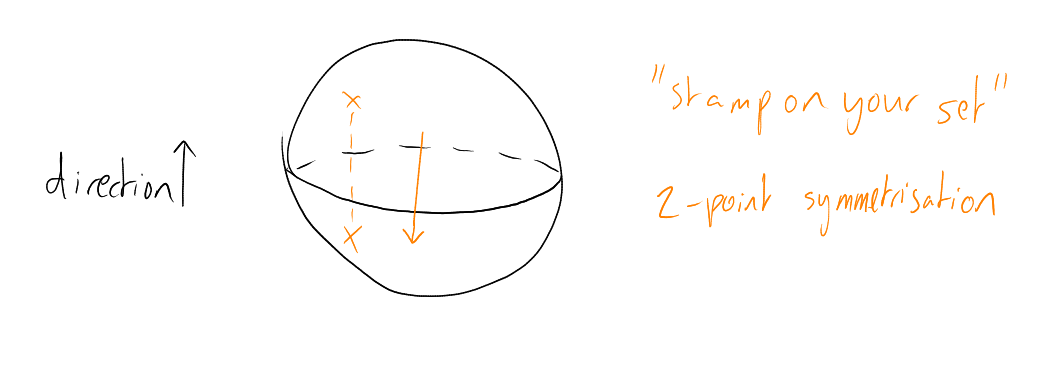
is a down-set (just down-compress, i.e. stamp on your set in direction
for each
). For any
, define
by giving
its -sections:
|
|
which will be a set of the form ,
or a complement. Write .
Do we have ?
Now, is
a down-set, so
|
|
and
The is because
not a down-set, as
extremal sets in dimension
are not nested.
Indeed, can have :
Idea: try to introduce a “fake” boundary :
want , with
on extremal
sets, such that
does decrease
(then done).
Try . Then
for all
, equality for extremal sets (as
equality for any down-set) and .
But: fails for
for all .
Could try to fix this by defining .
Also fails – for example if
is the “outer shell” of
then .
So far, have
where is the
extremal function in .
Now, is the pointwise minimum
of some functions of the form
and – each of which is a
concave function. Hence
itself is a concave function.
Consider varying ,
keeping constant
and keeping .
We obtain ,
where for some ,
So:
but is
still not a down-set.
Now vary, ,
keeping
fixed (
fixed) and .
This is a concave function of – as concave
+ concave + linear. Hence “make
as small or large as possible”.
i.e. ,
where one of the following holds:
-
for all
-
for all ,
for all
-
for all ,
for all .
But (miraculously), this
is a down-set!
Hence
|
|
So our “compression in direction ”
is: .
Now finish as before. □
Remark.
To make this precise, work instead in
(and then take a discrete approximation at the end).
End of non-examinable discussion.
Remark.
Very few isoperimetric inequalities are known (even approximately).
For example, “isoperimetric in a layer” – in the graph
, with
joined
if (i.e.
in
).
This is open. Nicest special case is ,
where it is conjectured that balls are best – i.e. sets of the form
.
3 Intersecting Families
3.1 -intersecting
families
is called
-intersecting
if for all
.
How large can a -intersecting
family be?
Example.
.
Could take
– has size .
Or – has
size .
Theorem 1 (Katona’s -intersecting Theorem).
Assuming that:
Then .
Proof.
For any :
have ,
so .
So, writing
for ,
have
– i.e.
disjoint from .
Suppose that .
Then, by Harper’s Theorem, we have
|
|
But
disjoint from ,
which has size
contradicting .
□
What about -intersecting
?
Might guess: best is .
Could also try ,
for .
Example.
For -intersecting
in:
-
:
,
,
.
-
:
,
,
.
-
:
,
,
.
Note that grows
quadratically,
linearly, and
constant – so
largest of these for
large.
Theorem 2.
Assuming that:
Then for sufficiently
large, we have .
Remark.
-
(1)
Bound we get on
would be
(crude) or
(careful).
-
(2)
Often called the “second Erdős-Ko-Rado Theorem”.
Idea of proof: “
has
degrees of freedom”.
Proof.
Extending
to a maximal -intersecting
family, we must have some
with
(if not, then by maximality have that ,
,
,
have
– whence ,
contradiction).
May assume that there exists
with –
otherwise all
have .
Whence .
So each
must meet
in
points. Thus
|
|
Note that the right hand side is a polynomial of degree
– so eventually
beaten by .
□
3.2 Modular Intersections
For intersecting families, we ban .
What if we banned ?
Example.
Want
with
odd for all distinct ?
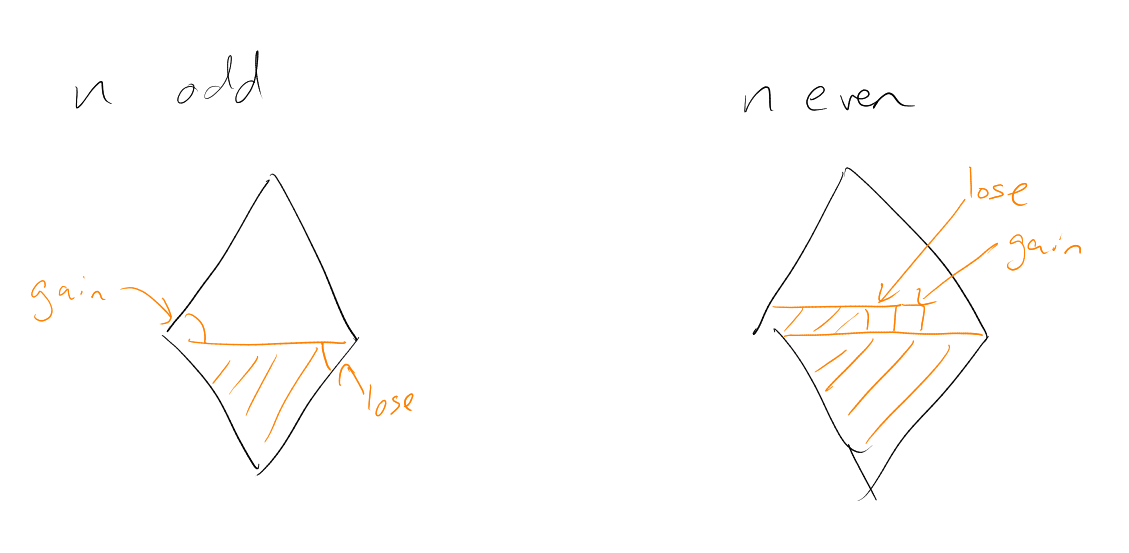
Try odd: can
achieve ,
by picture.
What if, still for
odd, had even
for all distinct ?
Can achieve ,
by picture.
This is only linear in .
Can we improve this?
Similarly if
even: For
even for all ,
can achieve
– picture
But for odd for
all (distinct):
can achieve
(as above). Can we improve this?
Seems to be that banning forces the
family to be very small (polynomial in ,
in fact a linear polynomial).
Remarkably, cannot beat linear.
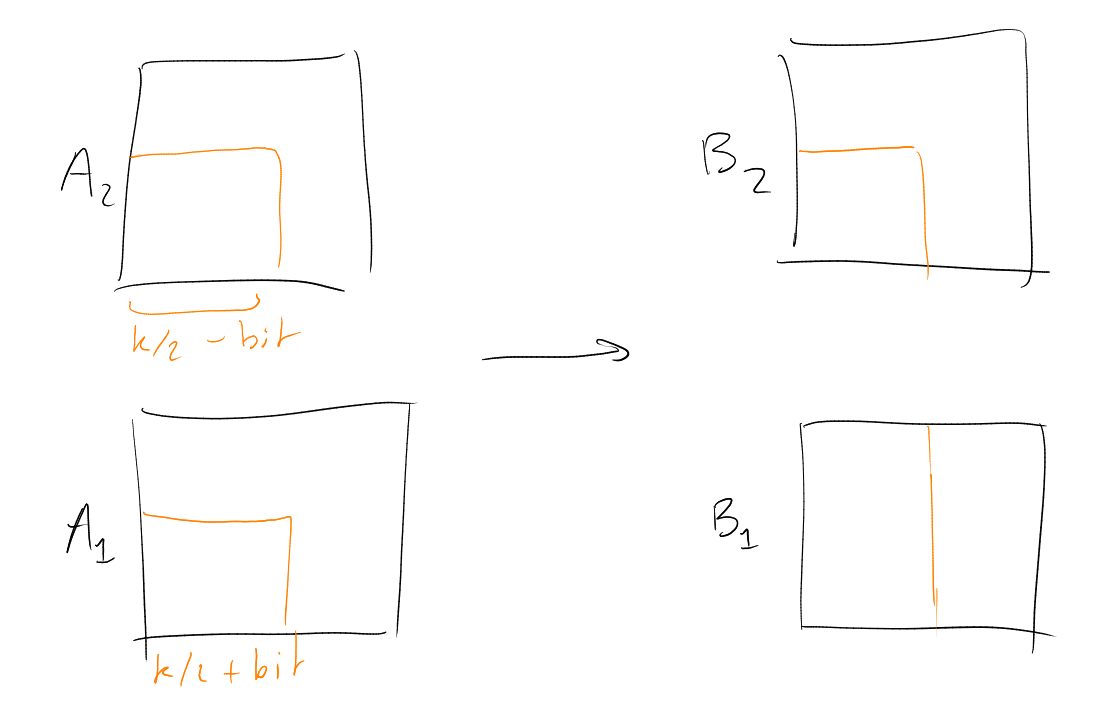
Proposition 3.
Assuming that:
Then .
Idea: Find
linearly independent vectors in a vector space of dimension
, namely
.
Proof.
View
as ,
the -dimensional
space over
(the field of order ).
By identifying
with ,
its characteristic sequence (e.g.
for ).
We have
for each ,
as
is odd (
is the usual dot-product).
Also,
for distinct
(as
even).
Hence the ,
are linearly independent (if ,
dot with
to get ).
□
Remark.
Hence also if ,
even, with
odd for
all distinct ,
then – just
add to each
and apply
Proposition 3 with .
Does this modulo
behaviour generalise?
Now show:
allowed values for
modulo implies
polynomial
of degree .
Theorem 4 (Frankl-Wilson Theorem).
Assuming that:
Then .
Remark.
-
(1)
This bound is a polynomial in
(as
vares)!
-
(2)
Bound is essentially best possible: can achieve
(see
picture).
-
(3)
Do need no .
Indeed, if
() then can
have with
(not a polynomial
in , as we can
choose any )
and all .
Idea: Try to find
linearly independent points in a vector space of dimension
, by somehow “applying
the polynomial
to ”.
Proof.
For each ,
let be the
matrix, with
rows indexed by ,
columns indexed by ,
with
|
|
for each ,
.
Let be the vector
space (over ) spanned
by the rows of .
So .
For , consider
(note each row
belongs to , as we
premultiplied by
a matrix). For ,
:
So
|
|
so all rows of
belong to .
Let (note each
row is in ).
For ,
have
Write the integer polynomial
as , with
– possible
because .
Let (each
row is in ).
Then for all :
|
|
So the submatrix of
spanned by the rows and columns corresponding to the elements of
is
|
|
Hence the rows of
corresponding to are
linearly independent over ,
so also over ,
so also over ,
so also over .
So .
□
Remark.
Do need prime.
Grolmusz constructed, for each ,
a value of and a
family such that
for all distinct
we have with
. This is not a
polynomial in .
Corollary 5.
Assuming that:
Then .
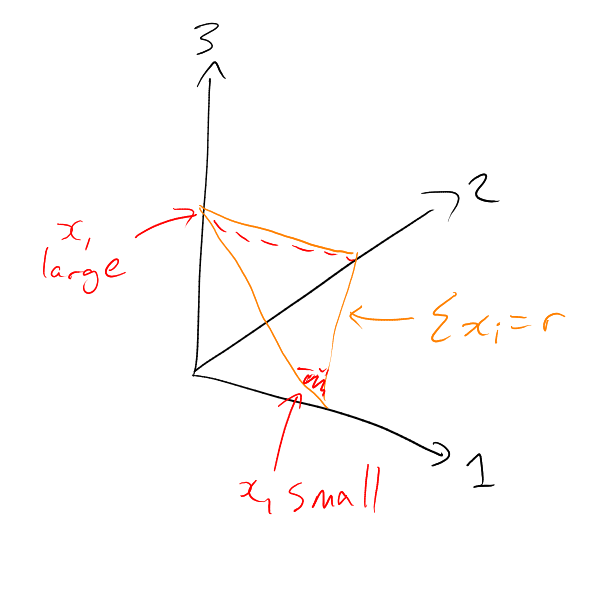
Two -sets in
typically meet
in about points
– but exactly
equaling is
very unlikely. But remarkably:
Corollary 6.
Assuming that:
Then .
Note.
is a tiny (exponentially
small) proportion of .
Indeed, (for
some )
whereas .
Proof.
Halving
if necessary, may assume that no
(any ).
Then
distinct implies ,
so .
So
by Corollary 5. □
3.3 Borsuk’s Conjecture
Let be a bounded
subset of .
How few pieces can we break
into such that each piece has smaller diameter than that of
?
The example of a regular simplex in
( points, all at
distance ) shows
that we may need
pieces.
Conjecture (Borsuk’s conjecture (1920s)).
pieces always sufficient.
Known for . Also known
for a smooth convex
body in or a symmetric
convex body in
(convex means
implies ).
However, Borsuk is massively false:
Theorem 7 (Kahn, Kalai 1995).
Assuming that:
Then there exists bounded
such that to break into pieces
of smaller diameter we need ,
for some constant
(not depending on ).
Note.
-
(1)
Our proof will show Borsuk’s conjecture (1920s) is false for .
-
(2)
We’ll prove it for
of the form ,
where
is prime. Then done for all
(with a different ,
e.g. because there exists a prime
with ).
Proof.
We’ll find
– in fact
for some .
We have already had two genuine ideas from this sentence: first that we think about having ,
and second that we go for .
Have ,
so :
|
|
So seek with
diameter , but
every subset of
with is
very small (hence we will need many pieces).
Identify with the
edge-set of , the
complete graph on
points.
For each let
be the complete bipartite
graph, with vertex classes .
Let . So
, and
.
Now
where .
This is minimised when ,
i.e. when .
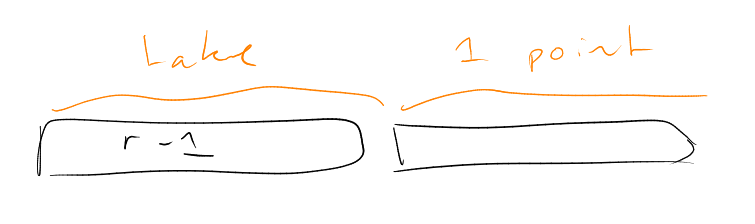
Now let have smaller
diameter than that of :
say . So must
have distinct:
(else diameter
of is the
diameter of ).
Thus
Conclusion: the number of pieces needed is
(for some ).
This is , for
some , which
is at least
for some .
□
˙
Index
antichain
boundary
chain
colexicographic
discrete cube
edge-boundary
grid
-compressed
Hamming ball
-binary
compressed
-compressed
-compression
intersecting
F
left-compressed
lexicographic
Lévy family
Lipschitz
median
neighbourhood
-section
-set
shadow
simplicial ordering
simplicial order
set system
-intersecting
-compression
-compressed