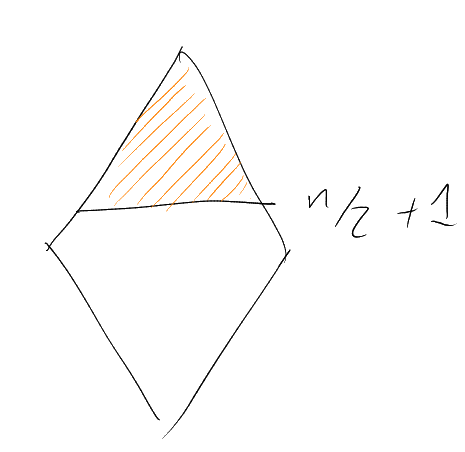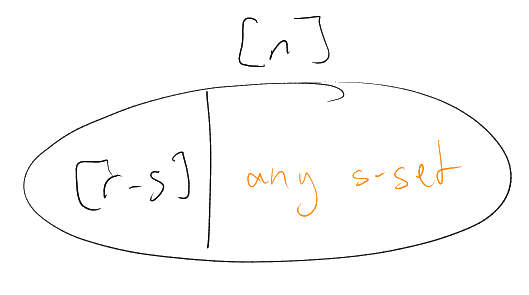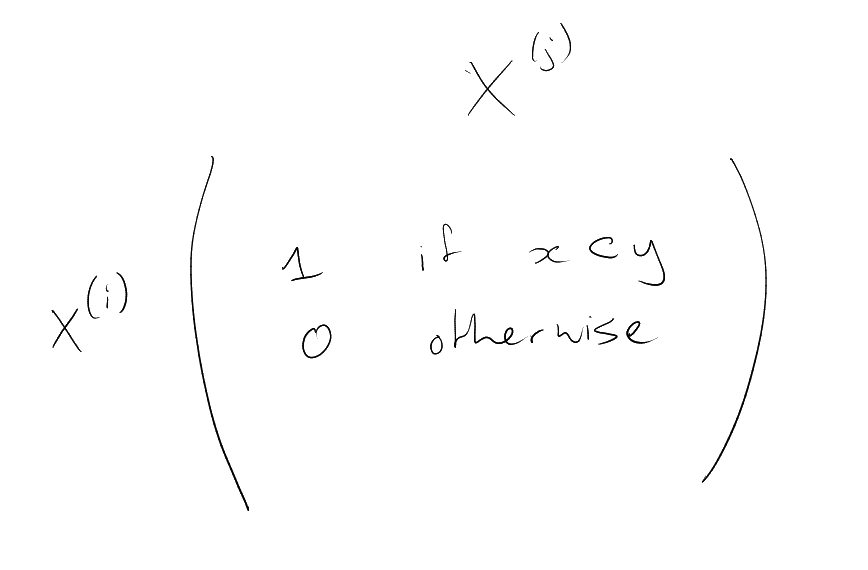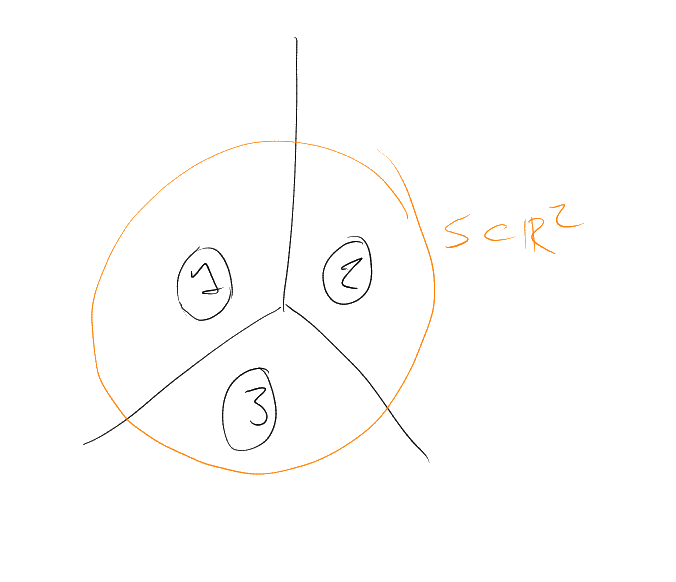Intersecting Families - Combinatorics

3 Intersecting Families

3.1 $t$ -intersecting families

$A \subset P (X)$ is called $t$ -intersecting if $| x \cap y | \geq t$ for all $x, y \in A$ .

How large can a $t$ -intersecting family be?

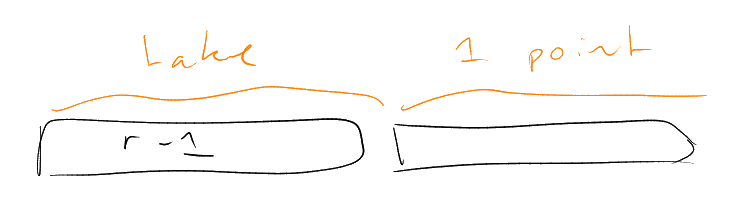
Example. $t = 2$ . Could take ${x : 1, 2 \in x}$ – has size $\frac{1}{4} 2^{n}$ . Or ${x : | x | \geq \frac{n}{2} + 1}$ – has size $\sim \frac{1}{2} 2^{n}$ .

Theorem 1 (Katona’s $t$ -intersecting Theorem). Assuming that:

$A \subset P (X)$ is $t$ -intersecting
$n + t$ even (to make the proof simpler – same proof works for odd)

Then

| A | \leq | X^{(\geq \frac{n + t}{2})} |

Proof. For any $x, y \in A$ : have $| x \cap y | \geq t$ , so $d (x, y^{c}) \geq t$ . So, writing $\bar{A}$ for ${y^{c} : y \in A}$ , have $d (A, \bar{A}) \geq t$ – i.e. $A_{(t - 1)}$ disjoint from $\bar{A}$ . Suppose that $| A | > | X^{(\geq \frac{n + t}{2})} |$ .

Then, by Harper’s Theorem, we have

| A_{(t - 1)} | \geq | X^{(\geq \frac{n + t}{2} - (t - 1))} | = | X^{(\geq \frac{n - t}{2} + 1)} | .

But $A_{(t - 1)}$ disjoint from $\bar{A}$ , which has size $> | X^{(\leq \frac{n - t}{2})} |$ contradicting $| A_{(t - 1)} | + | \bar{A} | \leq 2^{n}$ . □

What about $t$ -intersecting $A \subset X^{(r)}$ ?

Might guess: best is $A_{0} = {x \in X^{(r)} : [t] \subset x}$ .

Could also try $A_{α} = {x \in X^{(r)} : | x \cap [t + 2 α] | \geq t + α}$ , for $α = 1, 2, \dots, r - t$ .

Example. For $2$ -intersecting in:

${[7]}^{(4)}$ : $| A_{0} | = (\binom{5}{2}) = 10$ , $| A_{1} | = 1 + (\binom{4}{3}) (\binom{3}{1}) = 13$ , $| A_{2} | = (\binom{6}{4}) = 15$ .
${[8]}^{(4)}$ : $| A_{0} | = (\binom{6}{2}) = 15$ , $| A_{1} | = 1 + (\binom{4}{3}) (\binom{4}{1}) = 17$ , $| A_{2} | = (\binom{6}{4}) = 15$ .
${[9]}^{(4)}$ : $| A_{0} | = (\binom{7}{2}) = 21$ , $| A_{1} | = 1 + (\binom{4}{3}) (\binom{5}{1}) = 21$ , $| A_{2} | = (\binom{6}{4}) = 15$ .

Note that $| A_{0} |$ grows quadratically, $| A_{1} |$ linearly, and $| A_{2} |$ constant – so $| A_{0} |$ largest of these for $n$ large.

Theorem 2. Assuming that:

$A \subset X^{(r)}$ is $t$ -intersecting

Then for

n

sufficiently large, we have

| A | \leq | A_{0} | = (\binom{n - t}{r - t})

Remark.

(1) Bound we get on $n$ would be ${(16 r)}^{r}$ (crude) or $2 t r^{3}$ (careful).
(2) Often called the “second Erdős-Ko-Rado Theorem”.

Idea of proof: “ $A_{0}$ has $r - t$ degrees of freedom”.

Proof. Extending $A$ to a maximal $t$ -intersecting family, we must have some $x, y \in A$ with $| x \cap y | = t$ (if not, then by maximality have that $\forall x \in A$ , $\forall i \in x$ , $\forall j \notin x$ , have $x \cup j - i \in A$ – whence $A = X^{(r)}$ , contradiction).

May assume that there exists $z \in A$ with $x \cap y ⁄ \subset z$ – otherwise all $z \in A$ have $x \cap y \subset z$ . Whence $| A | \leq (\binom{n - t}{r - t}) = | A_{0} |$ .

So each $w \in A$ must meet $x \cup y \cup z$ in $\geq t + 1$ points. Thus

| A | \leq \underset{w on x \cup y \cup z}{\underset{⏟}{2^{3 r}}} (\underset{w off x \cup y \cup z}{\underset{⏟}{(\binom{n}{r - t - 1}) + (\binom{n}{r - t - 2}) + \dots + (\binom{n}{0})}}) .

Note that the right hand side is a polynomial of degree $r - t - 1$ – so eventually beaten by $| A_{0} |$ . □

3.2 Modular Intersections

For intersecting families, we ban $| x \cap y | = 0$ .

What if we banned $| x \cap y | \equiv 0 (m o d something)$ ?

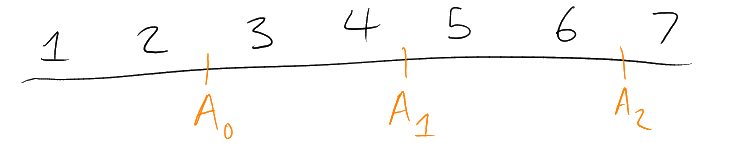
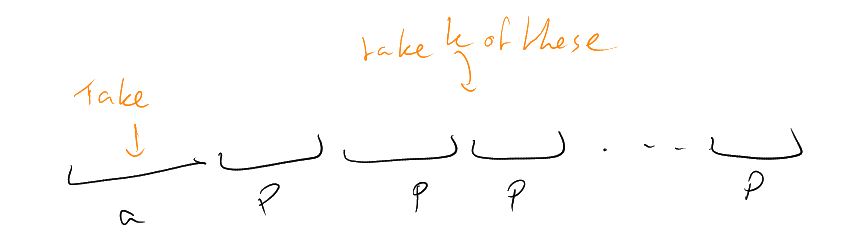
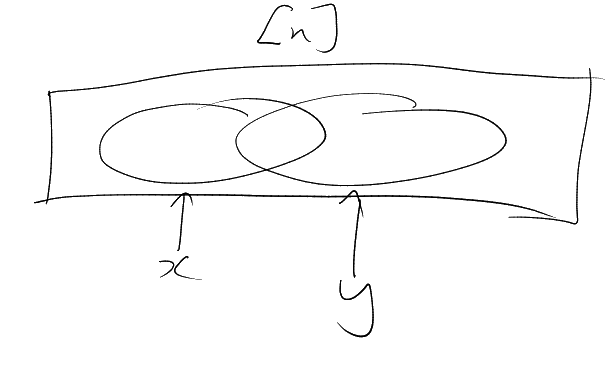
Example. Want $A \subset X^{(r)}$ with $| x \cap y |$ odd for all distinct $x, y \in A$ ?

Try $r$ odd: can achieve $| A | = (\binom{⌊ \frac{n - 1}{2} ⌋}{\frac{r - 1}{2}})$ , by picture.

What if, still for $r$ odd, had $| x \cap y |$ even for all distinct $x, y \in A$ ? Can achieve $n - r + 1$ , by picture.

This is only linear in $n$ . Can we improve this?

Similarly if $r$ even: For $| x \cap y |$ even for all $x, y \in A$ , can achieve $| A | = (\binom{⌊ \frac{n}{2} ⌋}{\frac{r}{2}})$ – picture

But for $| x \cap y |$ odd for all $x, y \in A$ (distinct): can achieve $n - r + 1$ (as above). Can we improve this?

Seems to be that banning $| x \cap y | = r (m o d 2)$ forces the family to be very small (polynomial in $n$ , in fact a linear polynomial).

Remarkably, cannot beat linear.

Proposition 3. Assuming that:

$r$ is odd
$A \subset X^{(r)}$ such that $| x \cap y |$ even for each distinct $x, y \in A$

Then

| A | \leq n

Idea: Find $| A |$ linearly independent vectors in a vector space of dimension $n$ , namely $Q_{n}$ .

Proof. View $P (X)$ as $ℤ_{2}^{n}$ , the $n$ -dimensional space over $ℤ_{2}$ (the field of order $2$ ). By identifying $x$ with $\bar{x}$ , its characteristic sequence (e.g. $1011000 \dots$ for ${1, 3, 4}$ ).

We have $(\bar{x}, \bar{x}) \neq 0$ for each $x$ , as $r$ is odd ( $(∙, ∙)$ is the usual dot-product).

Also, $(\bar{x}, \bar{y}) = 0$ for distinct $x, y \in A$ (as $| x \cap y |$ even).

Hence the $\bar{x}$ , $x \in A$ are linearly independent (if $\sum λ_{i} \bar{x_{i}} = 0$ , dot with $\bar{x_{j}}$ to get $λ_{j} = 0$ ). □

Remark. Hence also if $A \subset X^{(r)}$ , $r$ even, with $| x \cap y |$ odd for all distinct $x, y \in A$ , then $| A | \leq n + 1$ – just add $n + 1$ to each $x \in A$ and apply Proposition 3 with $X = [n + 1]$ .

Does this modulo $2$ behaviour generalise?

Now show: $s$ allowed values for $| x \cap y |$ modulo $p$ implies $| A | \leq$ polynomial of degree $s$ .

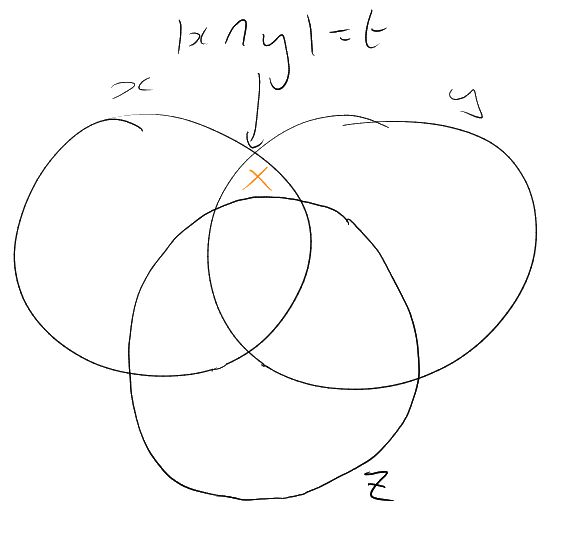
Theorem 4 (Frankl-Wilson Theorem). Assuming that:

$p$ is prime
$λ_{1}, \dots, λ_{s}$ ( $s \leq r$ )
$λ_{i} ⁄ \equiv r (m o d p)$ for each $i$
$A \subset X^{(r)}$ such that for all distinct $x, y \in A$ have $| x \cap y | \equiv λ_{i} (m o d p)$ for some $i$

Then

| A | \leq (\binom{n}{s})

Remark.

(1) This bound is a polynomial in $S$ (as $r$ vares)!
(2) Bound is essentially best possible: can achieve $| A | = (\binom{n}{n - r + s}) \sim (\binom{n}{s})$ (see picture).
(3) Do need no $λ_{i} \equiv r (m o d p)$ . Indeed, if $n = a + λ p$ ( $0 \leq a \leq p - 1$ ) then can have $A \subset^{(a + k p)}$ with $| A | = (\binom{λ}{k})$ (not a polynomial in $n$ , as we can choose any $k$ ) and all $| x \cap y | \equiv a (m o d p)$ .

Idea: Try to find $| A |$ linearly independent points in a vector space of dimension $(\binom{n}{s})$ , by somehow “applying the polynomial $(t - λ_{1}) \dots (t - λ_{s})$ to $| x \cap y |$ ”.

Proof. For each $i \leq j$ , let $M (i, j)$ be the $(\binom{n}{i}) \times (\binom{n}{j})$ matrix, with rows indexed by $X^{(i)}$ , columns indexed by $X^{(j)}$ , with

M {(i, j)}_{x y} = {\begin{matrix} 1 & if x \subset y \\ 0 & otherwise \end{matrix}

for each $x \in X^{(i)}$ , $y \in X^{(j)}$ .

Let $V$ be the vector space (over $ℝ$ ) spanned by the rows of $M (s, r)$ . So $\dim V \leq (\binom{n}{s})$ .

For $i \leq s$ , consider $M (i, s) M (s, r)$ (note each row belongs to $V$ , as we premultiplied $M (s, r)$ by a matrix). For $x \in X^{(i)}$ , $y \in X^{(r)}$ :

\begin{array}{l} {(M (i, s) M (s, r))}_{x y} & = # of s -sets z with x \subset z and z \subset y \\ = {\begin{matrix} 0 & if x ⁄ \subset y \\ (\binom{r - i}{s - i}) & if x \subset y \end{matrix} \end{array}

M (i, s) M (s, r) = (\binom{r - i}{s - i}) M (i, r)

so all rows of $M (i, r)$ belong to $V$ .

Let $M (i) = M {(i, r)}^{⊤} M (i, r)$ (note each row is in $V$ ).

For $x, y \in X^{(r)}$ , have

\begin{array}{l} M {(i)}_{x y} & = # i -sets z with z \subset x, z \subset y \\ = (\binom{| x \cap y |}{i}) \end{array}

Write the integer polynomial $(t - λ_{1}) \dots (t - λ_{s})$ as $\sum_{i = 0}^{s} a_{i} (\binom{t}{i})$ , with $a_{i} \in ℤ$ – possible because $t (t - 1) \dots (t - i + 1) = i! (\binom{t}{i})$ .

Let $M = \sum_{i = 0}^{s} a_{i} M (i)$ (each row is in $V$ ).

Then for all $x, y \in X^{(r)}$ :

M_{x y} = \sum_{i} a_{i} (\binom{| x \cap y |}{i}) = (| x \cap y | - λ_{i}) \dots (| x \cap y | - λ_{s}) .

So the submatrix of $M$ spanned by the rows and columns corresponding to the elements of $A$ is

(\begin{matrix} ⁄ \equiv 0 & 0 & \dots & 0 \\ 0 & ⁄ \equiv 0 & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & ⁄ \equiv 0 \end{matrix}) .

Hence the rows of $M$ corresponding to $A$ are linearly independent over $ℤ_{p}$ , so also over $ℤ$ , so also over $ℚ$ , so also over $ℝ$ .

So $| A | \leq \dim V \leq (\binom{n}{s})$ . □

Remark. Do need $p$ prime. Grolmusz constructed, for each $n$ , a value of $r \equiv 0 (m o d 6)$ and a family $A \subset {[n]}^{(r)}$ such that for all distinct $x, y \in A$ we have $| x \cap y | ⁄ \equiv 0 (m o d 6)$ with $| A | > n^{c \log n ∕ \log \log n}$ . This is not a polynomial in $n$ .

Corollary 5. Assuming that:

$A \subset {[n]}^{(r)}$ with $| x \cap y | ⁄ \equiv r (m o d p)$ , for each distinct $x, y \in A$ , where $p < r$ is prime

Then

| A | \leq (\binom{n}{p - 1})

Proof. We are allowed $p - 1$ values of $| x \cap y | (m o d p)$ , so done by Frankl-Wilson Theorem. □

Two $\frac{n}{2}$ -sets in $[n]$ typically meet in about $\frac{n}{4}$ points – but $| x \cap y |$ exactly equaling $\frac{n}{4}$ is very unlikely. But remarkably:

Corollary 6. Assuming that:

$p$ is prime, and let $A \subset {[4 p]}^{(2 p)}$ have $| x \cap y | \neq p$ for all distinct $x, y \in A$ (“this is not much of a constraint”)

Then

| A | \leq 2 (\binom{4 p}{p - 1})

Note. $(\binom{4 p}{p - 1})$ is a tiny (exponentially small) proportion of $(\binom{4 p}{2 p})$ . Indeed, $(\binom{n}{n ∕ 2}) \sim c \cdot \frac{2^{n}}{\sqrt{n}}$ (for some $c$ ) whereas $(\binom{n}{n ∕ 4}) \leq 2 e^{- n ∕ 32} 2^{n}$ .

Proof. Halving $| A |$ if necessary, may assume that no $x, x^{c} \in A$ (any $x \in {[4 p]}^{(2 p)}$ ).

Then $x, y \in A$ distinct implies $| x \cap y | \neq 0, p$ , so $| x \cap y | ⁄ \equiv 0 (m o d p)$ .

So $| A | \leq (\binom{4 p}{p - 1})$ by Corollary 5. □

3.3 Borsuk’s Conjecture

Let $S$ be a bounded subset of $ℝ^{n}$ .

How few pieces can we break $S$ into such that each piece has smaller diameter than that of $S$ ?

The example of a regular simplex in $ℝ^{n}$ ( $n + 1$ points, all at distance $1$ ) shows that we may need $n + 1$ pieces.

Conjecture (Borsuk’s conjecture (1920s)). $n + 1$ pieces always sufficient.

Known for $n = 1, 2, 3$ . Also known for $S$ a smooth convex body in $ℝ^{n}$ or a symmetric convex body in $ℝ^{n}$ (convex means $x \in S$ implies $- x \in S$ ).

However, Borsuk is massively false:

Theorem 7 (Kahn, Kalai 1995). Assuming that:

$n \in ℕ$

Then there exists bounded

S \subset ℝ^{n}

such that to break

S

into pieces of smaller diameter we need

\geq C^{\sqrt{n}}

, for some constant

c > 1

(not depending on

n

Note.

(1) Our proof will show Borsuk’s conjecture (1920s) is false for $n \geq 2000$ .
(2) We’ll prove it for $n$ of the form $(\binom{4 p}{2})$ , where $p$ is prime. Then done for all $n$ (with a different $c$ , e.g. because there exists a prime $p$ with $\frac{n}{2} \leq p \leq n$ ).

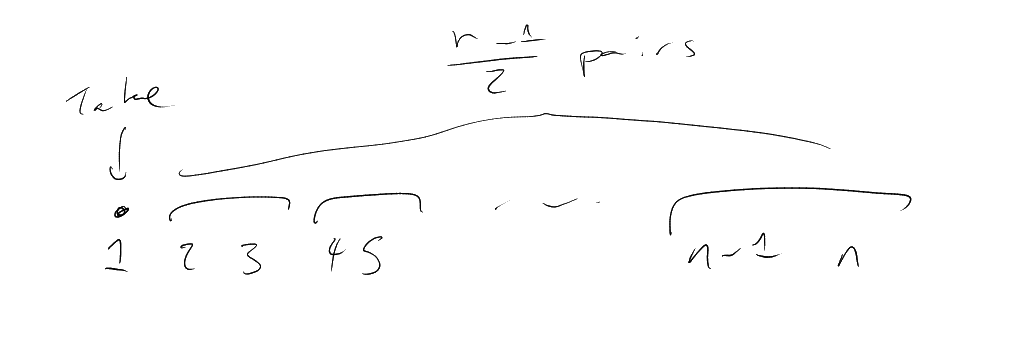
Proof. We’ll find $S \subset Q_{n} \subset ℝ^{n}$ – in fact $S \subset {[n]}^{(r)}$ for some $r$ . We have already had two genuine ideas from this sentence: first that we think about having $S \subset Q_{n}$ , and second that we go for $S \subset {[n]}^{(r)}$ .

Have $S \subset {[n]}^{(r)}$ , so $\forall x, y \in S$ :

∥ x - y ∥^{2} = # coordinates where x and y differ = 2 (r - | x \cap y |) .

So seek $S$ with diameter $\min | x \cap y | = k$ , but every subset of $S$ with $\min | x \cap y | > k$ is very small (hence we will need many pieces).

Identify $[n]$ with the edge-set of $K_{4 p}$ , the complete graph on $4 p$ points.

For each $x \in {[4 p]}^{(2 p)}$ let $G_{x}$ be the complete bipartite graph, with vertex classes $x, x^{c}$ . Let $S = {G_{x} : x \in {[4 p]}^{(2 p)}}$ . So $S \subset {[n]}^{(4 p^{2})}$ , and $| S | = \frac{1}{2} (\binom{4 p}{2 p})$ .

Now

\begin{array}{l} | G_{x} \cap G_{y} | & = | x \cap y | | x^{c} \cap y^{c} | + | x^{c} \cap y | | x \cap y^{c} | \\ = | x \cap y |^{2} + | x^{c} \cap y |^{2} \\ = d^{2} + {(2 p - d)}^{2} \end{array}

where $d = | x \cap y |$ .

This is minimised when $d = p$ , i.e. when $| x \cap y | = p$ .

Now let $S^{'} \subset S$ have smaller diameter than that of $S$ : say $S^{'} = {G_{x} : x \in A}$ . So must have $\forall x, y \in A$ distinct: $| x \cap y | \neq p$ (else diameter of $S^{'}$ is the diameter of $S$ ).

Thus

| A | \leq 2 (\binom{4 p}{p - 1}) .

Conclusion: the number of pieces needed is $\geq \frac{\frac{1}{2} (\binom{4 p}{2 p})}{2 (\binom{4 p}{p - 1})} \geq \frac{c \cdot 2^{4 p} ∕ \sqrt{p}}{e^{- p ∕ 8} 2^{4 p}}$ (for some $c$ ). This is $\geq {(c^{'})}^{p}$ , for some $c^{'} > 1$ , which is at least ${(c^{″})}^{\sqrt{n}}$ for some $c^{″} > 1$ . □

3 Intersecting Families

3.1 t-intersecting families

3.2 Modular Intersections

3.3 Borsuk’s Conjecture

3.1 $t$ -intersecting families