Introduction to
Additive Combinatorics
Daniel Naylor
Contents
1 Combinatorial methods
Definition 1.1 (Sumset).
Let
be an abelian group. Given ,
define the sumset
to be
|
|
and the difference set
to be
|
|
If and
are
finite, then certainly
|
|
Example 1.2.
Let .
Then
|
|
Lemma 1.3.
Assuming that:
Then , with equality
if and only if
is an arithmetic progression.
Proof.
Let
with .
Then
|
|
so . But
we could also have written
|
|
When ,
these two orderings must be the same. So
for all .
□
Exercise: If , then
with equality
if and only if
and are
arithmetic progressions with the same common difference.
Example 1.4.
Let
with prime.
Then .
Indeed,
(note that
means ).
But ,
|
|
Theorem 1.5 (Cauchy-Davenport).
Assuming that:
-
is a prime
-
nonempty
Then |
|
Proof.
Assume .
Without loss of generality assume that
and that .
Apply induction on .
The case
is trivial. Suppose ,
and let .
Since
and ,
there must exist
such that
but .
Let ,
so ,
,
.
But , so the inductive
hypothesis applies to
and .
Since
|
|
we have
|
|
This fails for general abelian groups (or even general cyclic groups).
Example 1.6.
Let be
(fixed, small) prime, and let
be a subspace. Then ,
so . In fact,
if is such
that ,
then
must be a coset of a subspace.
Example 1.7.
Let
be such that .
Then there exists
a subspace such that
and is contained
in a coset of .
See Example Sheet 1.
Definition 1.8 (Ruzsa distance).
Given finite sets
, we define the
Ruzsa distance
between
and by
|
|
Note that this is symmetric, but is not necessarily non-negative, so we cannot prove that it is a metric. It
does, however, satisfy triangle inequality:
Lemma 1.9 (Ruzsa’s triangle inequality).
Assuming that:
Then |
|
Proof.
Observe that
Indeed, writing each
as with
,
, the
map
is injective. The triangle inequality now follows from the definition. □
Definition 1.10 (Doubling / difference constant).
Given a finite
, we
write
for the doubling constant of
and
for the difference constant of .
Then Lemma 1.9 shows, for example, that
|
|
So , or
.
Notation.
Given
and , we
write
|
|
Theorem 1.11 (Plunnecke’s Inequality).
Assuming that:
Proof.
Choose a non-empty subset
such that the ratio
is minimised, and call this ratio .
Then ,
,
and ,
.
Claim: For every finite ,
.
Let’s complete the proof of the theorem assuming the claim. We first show that
,
. Indeed, the case
is trivial, and
is true by assumption.
Suppose and the
inequality holds for .
By the claim with ,
we get
|
|
But as in the proof of Ruzsa’s triangle inequality,
, we can
show
|
|
Hence ,
which completes the proof (assuming the claim).
We now prove the claim by induction on .
When
the statement follows from the assumptions. Suppose the claim is true for
, and
consider for
some .
Observe that
|
|
with .
By definition of ,
,
so
We apply this argument a second time, writing
|
|
where .
We conclude that
|
|
so
|
|
proving the claim. □
We are now in a position to generalise Example 1.7.
Theorem 1.12 (Freiman-Ruzsa).
Assuming that:
Then is contained
in a subspace
of size .
Proof.
Choose maximal
such that the translates
with are disjoint.
Such a set cannot
be too large: ,
, so by Plunnecke’s
Inequality, since ,
|
|
So . We
next show
Indeed, if
and ,
then by maximality of ,
for some
(and if ,
then clearly ).
It follows from ()
by induction that ,
|
|
since
|
|
Now let be the
subgroup generated by ,
which we can write as
|
|
where
is the subgroup generated by .
But every element of can
be written as a sum of
elements of with
coefficients amongst ,
hence .
To conclude, note that
|
|
where we use Plunnecke’s Inequality or even Ruzsa’s triangle inequality. □
Example 1.13.
Let
where
is a subspace of dimension
and
consists of
linearly independent vectors not in .
Then
|
|
and
|
|
But any subspace
containing must have
size at least , so the
exponential dependence on
is necessary.
Theorem 1.14 (Polynomial Freiman-Ruzsa, due to Gowers–Green–Manners–Tao 2024).
Assuming
that:
Then there exists a subspace
of size at most
such
that for some
,
|
|
where
and are
polynomial in .
Proof.
Omitted, because the techniques are not relevant to other parts of the course. See Entropy
Methods in Combinatorics next term. □
Definition 1.15.
Given we
define the additive energy between
and to
be
|
|
We refer to the quadruples
such that
as additive quadruples.
Example 1.16.
Let
be a subspace. Then .
On the other hand, if is chosen at
random from (each element chosen
independently with probability ),
then with high probability
|
|
Lemma 1.17.
Assuming that:
Then |
|
Proof.
Define (and notice
that this is the same as ).
Observe that
but
(As usual,
here means the indicator function). □
In particular, if ,
then
|
|
The converse is not true.
Example 1.18.
Let
be your favourite (class of) abelian group(s). Then there exist constants
such that for all
sufficiently large ,
there exists ,
with
satisfying
and .
Theorem 1.19 (Balog–Szemeredi–Gowers, Schoen).
Assuming that:
Then there exists
of size at least
such that ,
where
and are
polynomial in .
Idea: Find
such that such
that has many
representations as
with .
We first prove a technical lemma, using a technique called “dependent random choice”.
Definition 1.20 (gamma-popular differences).
Given
and
, let
|
|
be the set of -popular
differences of .
Lemma 1.21.
Assuming that:
-
is finite
-
-
Then there is a subset
of size such that for
all but a -proportion
of pairs ,
.
Proof.
Let .
Then
For , let
|
|
and set .
Then
Let .
Then
Hence there exists
such that
|
|
Let ,
,
. So
|
|
Find such
that is
large.
Given ,
let .
Then
|
|
Let .
Then
Therefore,
So there exists
such that ,
in which case we have
and .
□
Proof of Theorem 1.19.
Given
with , apply
Lemma 1.21 with
to otain of
size such that
for all but
of pairs ,
. In
particular, the bipartite graph
|
|
has at least
edges. Let .
Clearly, . For
any , there
are at least
elements
such that
().
Thus
has at least
|
|
representations of the form
with .
It follows that
Thus .
□
2 Fourier-analytic techniques
In this chapter we will assume that
is finite abelian.
comes equipped with
a group of characters,
i.e. homomorphisms .
In fact, is
isomorphic to .
See Representation Theory notes for more information about characters and proofs of this as well as some of
the facts below.
Example 2.1.
-
(i)
If ,
then for any ,
we have an associated character ,
where .
-
(ii)
If ,
then any
can be associated to a character .
Notation.
Given
nonempty, and any function ,
let
|
|
Lemma 2.2.
Assuming that:
Then |
|
and for all ,
|
|
Proof.
The first equality in eqch case is trivial. Suppose
. Then there
exists
with .
Then
So .
For the second part, note that given ,
there must by such
that , for otherwise
would act trivially on
, hence would also be
the dual group for ,
a contradiction. □
Definition 2.3 (Fourier transform).
Given ,
define its Fourier transform
by
It is easy to verify the inversion formula: for all ,
Indeed,
Given , the indicator or
characteristic function of ,
is
defined as usual.
Note that
|
|
The density of
in (often
denoted by ).
Definition (Characteristic measure).
Given non-empty ,
the characteristic measure
is defined by .
Note that .
Definition (Balanced function).
The balanced function
is given by
. Note
that .
Example 2.4.
Let
be a subspace. Then for ,
we have
where is the
annihilator of .
In other words, .
Example 2.5.
Let
be such that each
lies in independently
with probability .
Then with high probability
|
|
This follows from Chernoff’s inequality: Given
-valued independent
random variables
with mean ,
then for all ,
we have
|
|
Example 2.6.
Let
with .
Then
and .
Given ,
we write
|
|
Consequently,
|
|
Lemma 2.7.
Assuming that:
Then
-
(i)
(Parseval’s identity)
-
(ii)
(Plancherel’s identity)
Proof.
Exercise (hopefully easy). □
Definition 2.8 (Spectrum).
Let
and . Define
the -large
spectrum of
to be
|
|
Example 2.9.
By Example 2.4, if
with ,
then ,
|
|
Lemma 2.10.
Assuming that:
Then |
|
Proof.
By Parseval’s identity,
In particular, if
for ,
then
|
|
so .
Definition 2.11 (Convolution).
Given ,
we define their convolution
by
|
|
Example 2.12.
Given ,
|
|
In particular, .
Lemma 2.13.
Assuming that:
Then |
|
Proof.
Example 2.14.
|
|
In particular,
for any .
Theorem 2.15 (Bogolyubov’s lemma).
Assuming that:
Then there exists
of codimension
such that .
Proof.
Observe
|
|
so wish to find
such that
for all . Let
with
and let
. By
Lemma 2.10, .
Fix .
Note
since
for all
and
hence (in
fact, )
for all
and .
□
Example 2.16.
The set
(where counts the
number of 1s in ) has
density , but there is no
coset of any subspace
of codimension
such that .
Lemma 2.17.
Assuming that:
-
of density
-
-
Then there exists
of codimension
and
such that
|
|
Proof.
Let be
such that ,
and let .
Write for
for the
distinct
cosets
of .
Then
By triangle inequality, .
But note that
so , hence
there exists
such that .
Then .
□
Notation.
Given ,
write
|
|
Notation.
Given ,
write
to be distinguished from .
Lemma 2.18.
Assuming that:
-
prime
-
of density
-
Then the number of 3-term arithmetic progressions in
differs from
by at
most .
Proof.
The number of 3-term arithmetic progressions in
is
times
By Plancherel’s identity and Lemma 2.13, we have
but
by Parseval’s identity. □
Theorem 2.19 (Meshulam’s Theorem).
Assuming that:
Then .
Proof.
By assumption,
|
|
But as in (the proof of) Lemma 2.18,
|
|
so provided ,
i.e.
we have .
So by Lemma 2.17 with ,
there exists
of codimension 1 and
such that .
We iterate this observation: let ,
,
. At the
-th step, we are
given a set
of density
with no non-trivial 3 term arithmetic progressions. Provided that
, there
exists of
codimension ,
such
that
|
|
Set ,
has density ,
and is free of non-trivial 3 term arithmetic progressions.
Through this iteration, the density increases from
to
in at most
steps.
to
in at most
steps and so on.
So reaches
in at most
|
|
steps. The argument must end with ,
at which point we must have had ,
or else we could have continued.
But we may assume that
(or )
whence ,
or .
□
At the time of writing, the largest known subset of
containing no non-trivial 3 term arithmetic progressions has size
.
We will prove an upper bound of the form .
Theorem 2.20 (Roth’s theorem).
Assuming that:
Then .
Example 2.21 (Behrend’s example).
There exists
of size
at least
containing no non-trivial 3 term arithmetic progressions.
Lemma 2.22.
Assuming that:
Then one of the following holds:
-
(i)
(where the Fourier coefficient is computed in )
-
(ii)
There exists an interval
of length
such that
Proof.
We may assume that
since otherwise
so we would be in Case (ii) with .
Let . Note that all 3 term arithmetic
progressions of the form are in
fact arithmetic progressions in .
If or
were at least
, we would again be in case
(ii). So we may assume that .
Now as in Lemma 2.18 and Theorem 2.19,
where
and . So
as before,
|
|
provided that ,
i.e. .
(Check this is satisfied).
Hence
|
|
Lemma 2.23.
Assuming that:
Then there exists a partition of
into progressions
of length
such that
|
|
for all .
Proof.
Let
and consider .
By Pigeonhole, there exists such
that .
Set ,
so .
Divide
into residue classes modulo ,
each of which has size at least .
But each residue class can be divided into arithmetic progressions of the form
with .
The diameter of the image of each progression under
is .
□
Lemma 2.24.
Assuming that:
Then there exists a progression
of length at least
such that .
Proof.
Let , and use
Lemma 2.23 to partition
into progressions
of length
|
|
and . Fix
one from
each of the .
Then
So
|
|
Since
has mean zero,
|
|
hence there exists
such that
|
|
and so
|
|
Definition 2.25 (Bohr set).
Let
and . By the
Bohr set we
mean the set
|
|
We call
the rank of ,
and
its width or radius.
Example 2.26.
When ,
then for all
sufficiently small .
Lemma 2.27.
Assuming that:
Proposition 2.28 (Bogolyubov in a general finite abelian group).
Assuming that:
Then there exists
of size at most
such that .
Proof.
Recall .
Let , and note
that, for
and ,
. Hence,
for ,
|
|
and
|
|
3 Probabilistic Tools
All probability spaces in this course will be finite.
Theorem 3.1 (Khintchine’s inequality).
Assuming that:
-
-
independent random variables
-
Then |
|
Proof.
By nesting of norms, it suffices to prove the case
for some .
Write ,
and assume .
Note that in fact ,
hence .
By Chernoff’s inequality (Example 2.5), for all
we have
|
|
and so using the fact that
we have
We shall show by induction on
that . Indeed,
when ,
|
|
For ,
integrate by parts to find that
Corollary 3.2 (Rudin’s Inequality).
Let
be a linearly independent set and let .
Then for any ,
|
|
Corollary 3.3.
Let be a
linearly independent set and let .
Then for all ,
|
|
Proof.
Let
and write .
Then
which is bounded above by
where ,
using Hölder’s inequality.
By Rudin’s Inequality,
|
|
Recall that given
of density ,
we had .
This is best possible as the example of a subspace shows. However, in this case the large spectrum is highly
structured.
Theorem 3.4 (Special case of Chang’s Theorem).
Assuming that:
-
of density
-
Then there exists
of dimension
such that .
Proof.
Let be a maximal
linearly independent set. Let .
Clearly . By
Corollary 3.3, for all ,
|
|
so
|
|
Set
to get .
□
Definition 3.5 (Dissociated).
Let
be a finite abelian group. We say
is dissociated if
for ,
then .
Clearly, if ,
then is
dissociated if and only if it is linearly independent.
Theorem 3.6 (Chang’s Theorem).
Assuming that:
Then .
We may bootstrap Khintchine’s inequality to obtain the following:
Theorem 3.7 (Marcinkiewicz-Zygmund).
Assuming that:
Then |
|
Proof.
First assume the distribution of the ’s
is symmetric, i.e. for
all . Partition the
probability space
into sets , write
for the induced
measure on
such that all ’s
are symmetric and take at most 2 values. By Khintchine’s inequality, for each
,
so summing over all and taking
-th roots gives the symmetric
case. Now suppose the ’s
are arbitrary, and let
be such that and
are all independent. Applying
the symmetric case to ,
But then
concluding the proof. □
Theorem 3.8 (Croot-Sisask almost periodicity).
Assuming that:
Then there exists
and a set
such that
and
|
|
where for all
, and as a reminder,
is the characteristic
measure of .
Proof.
The main idea is to approximate
|
|
by ,
where
are sampled independently and uniformly from ,
and
is to be chosen later.
For each , define
. For each
, these are independent
random variables with mean ,
so by Marcinkiewicz-Zygmund,
By Hölder with ,
we get
so
|
|
Summing over all ,
we have
|
|
with
by Young / Hölder (
where ).
So we have
|
|
Choose so that the
RHS is at most .
whence
|
|
Write
|
|
By Markov inequality, since
|
|
we have
|
|
so . Let
|
|
Now ,
whence
|
|
By Lemma 1.17,
|
|
so there are at least
pairs such that
. In particular,
there exists
and of size
such that for
all , there
exists such
that for all ,
. But then
for each , by
the triangle inequality,
by definion of .
□
Theorem 3.9 (Bogolyubov again, after Sanders).
Assuming that:
Then there exists a subspace
of codimension
such tht .
Almost periodicity is also a key ingredient in recent work of Kelley and Meka, showing that any
containing no non-trivial 3 term arithmetic progressions has size
.
4 Further Topics
In , we
can do much better.
Theorem 4.1 (Ellenberg-Gijswijt, following Croot-Lev-Pach).
Assuming that:
Then .
Notation.
Let be the set of
monomials in whose degree
in each variable is at most .
Let be the vector
space over
whose basis is .
For any , write
for the set of
monomials in of (total)
degree at most , and
for the corresponding
vector space. Set .
Lemma 4.2.
Assuming that:
Then |
|
Proof.
Every can be written as a
linear combination of monomials in ,
so
|
|
for some coefficients .
Clearly at least one of
must have degree ,
whence
|
|
for some families of polynomials ,
.
Viewing
as a -matrix
,
we see that
can be written as the sum of at most
matrices, each of which has rank .
Thus .
But by assumption,
is a diagonal matrix whose rank equals .
□
Proposition 4.3.
Assuming that:
Then .
Proof.
Let be an integer to
be determined later. Let be
the space of polynomials in
that vanish on .
We have
|
|
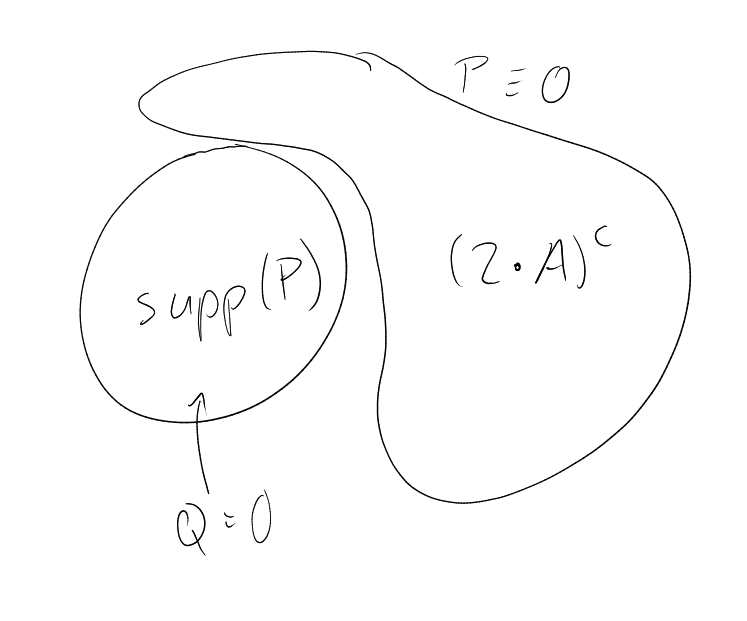
We claim that there exists
such that . Indeed, pick
with maximal support.
If , then there would be
a non-zero polynomial
vanishing on , in which
case , contradicting
the choice of .
Now by assumption,
|
|
So any polynomial that vanishes on
vanishes on .
By Lemma 4.2 we now have that,
Hence . But the
monomials in are in
bijection with the ones in
via , whence
. Thus
setting , we
have .
□
You will prove Theorem 4.1 on Example Sheet 3.
We do not have at present a comparable bound for 4 term arithmetic progressions. Fourier techniques also
fail.
Example 4.4.
Recall from Lemma 2.18 that given
,
|
|
But it is impossible to bound
|
|
by . Indeed,
consider .
By Problem 11(ii) on Sheet 1,
and
|
|
But given a 3 term arithmetic progression ,
by the identity
|
|
automatically
lies in ,
so
|
|
which is not close to .
Definition 4.5 (-norm).
Given , define
its -norm by
the formula
|
|
Problem 1(i) on Sheet 2 showed that ,
so this is indeed a norm.
Problem 1(ii) asserted the following:
Lemma 4.6.
Assuming that:
Then |
|
Note that
|
|
and thus by Parseval’s identity,
|
|
Hence
|
|
Moreover, if ,
then
|
|
We may therefore reformulate the first step in the proof of Meshulam’s Theorem as follows: if
, then
by Lemma 4.6,
|
|
It remains to show that if is non-trivial,
then there exists a subspace of
bounded codimension on which
has increased density.
Theorem 4.7 ( Inverse Theorem).
Assuming that:
-
-
-
-
Then there exists
such that
|
|
In other words,
for and
we say “
correlates with a linear phase function”.
Proof.
We have seen that
|
|
so
|
|
Definition 4.8 ( norm).
Given ,
define its
norm by
where and
denotes the
number of ones in .
It is easy to verify that
where .
Definition 4.9 ( inner product).
Given functions
for , define
their
inner product by
|
|
Observe that .
Lemma 4.10 (Gowers–Cauchy–Schwarz Inequality).
Assuming that:
Then |
|
Setting
for and
otherwise, it
follows that
hence .
Proposition 4.11.
Assuming that:
Then |
|
Proof.
We additionally assume
to make the proof easier to follow, but the same ideas are used for the general case. We additionally
assume ,
by rescaling, since the inequality is homogeneous.
Reparametrising, we have
Theorem 4.12 (Szemeredi’s Theorem for 4-APs).
Assuming that:
Then .
Idea: By Proposition 4.11 with ,
|
|
where
consists of
other terms in which between one and three of the inputs are equal to
.
These are controlled by
whence
|
|
So if contains no non-trivial 4
term arithmetic progressions and ,
then .
What can we say about functions with large
norm?
Example 4.13.
Let
be an symmetric
matrix with entries in .
Then
satisfies .
Theorem 4.14 ( inverse theorem).
Assuming that:
Then there exists a symmetric
matrix
with
entries in
and
such that
|
|
where is a
polynomial in .
In other words,
for and
we say “
correlates with a quadratic phase function”.
Proof (sketch).
Let
denote .
.
-
STEP 1:
Weak linearity. See reference.
-
STEP 2:
Strong linearity. We will spend the rest of the lecture discussing this in detail.
-
STEP 3:
Symmetry argument. Problem 8 on Sheet 3.
-
STEP 4:
Integration step. Problem 9 on Sheet 3.
STEP 1: If , then for
at least a -proportion
of ,
. So for each
such , there
exists such
that .
Proposition 4.15.
Assuming that:
-
-
-
-
Then there exists
with
and a
function
such that
-
(i)
;
-
(ii)
There are at least
quadruples
such that
and .
STEP 2: If and
are as above, then there
is a linear function
which coincides with
for many elements of .
Proposition 4.16.
Assuming that:
-
and
given as in Proposition
4.15
Then there exists
matrix with
entries in
and such
that
()
satisfies
for
elements .
Proof.
Consider the graph of ,
.
By Proposition 4.15,
has
additive quadruples.
By Balog–Szemeredi–Gowers, Schoen, there exists
with
and .
udefine
by
and note .
By Freiman-Ruzsa applied to ,
there exists a subspace
with
such that .
Denote by the projection
onto the first coordinates.
By construction, .
Moreover, since ,
|
|
We may thus partition
into cosets of some
subspace such that
is injective on each coset. By
averaging, there exists a coset
such that
|
|
Set ,
and define
accordingly.
Now
is injective and surjective onto .
This means there is an affine linear map
such that
for all .
□
Then do steps 3 and 4. □
What to do if you have lots of additive quadruples?
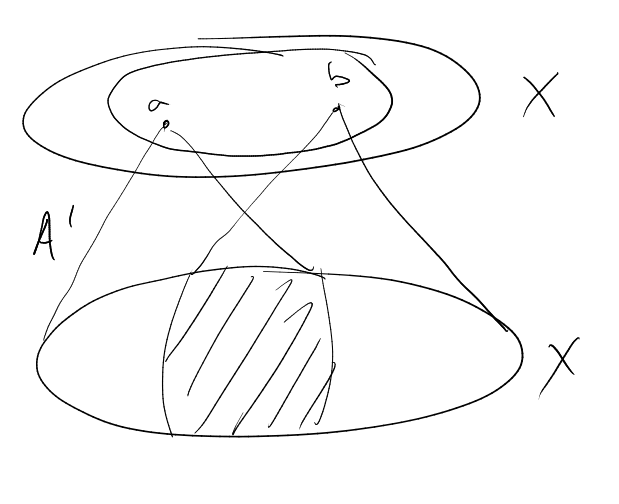
Balog-Szemeredi-Gowers
What to do if you have small doubling constant?
Freiman-Ruzsa (or Polynomial-Freiman-Ruzsa)
˙
Index
additive energy
additive quadruple
Bohr set
characteristic measure
Chernoff’s inequality
difference constant
dissociated
doubling constant
Parseval’s identity
Plancherel’s identity
Rusza distance
-large
spectrum of
sumset