Introduction to Additive Combinatorics

Introduction to Additive Combinatorics
Daniel Naylor

1Combinatorial methods
2Fourier-analytic techniques
3Probabilistic Tools
4Further Topics
Index

1 Combinatorial methods

Definition 1.1 (Sumset). Let $G$ be an abelian group. Given $A, B \subseteq G$ , define the sumset $A + B$ to be

A + B : = {a + b : a \in A, b \in B}

and the difference set $A - B$ to be

A - B : = {a + b : a \in A, b \in B} .

If $A$ and $B$ are finite, then certainly

\max {| A |, | B |} \leq | A + B | \leq | A | | B | .

Example 1.2. Let $A = [n] : = {1, 2, \dots, n} \subseteq ℤ$ . Then

| A + A | = | {2, \dots, 2 n} | = 2 n - 1 = 2 | A | - 1 .

Lemma 1.3. Assuming that:

$A \subseteq ℤ$ is finite.

Then

| A + A | \geq 2 | A | - 1

, with equality if and only if

A

is an arithmetic progression.

Proof. Let $A = {a_{1}, a_{2}, \dots, a_{n}}$ with $a_{1} < a_{2} < \dots < a_{n}$ . Then

a_{1} + a_{1} < a_{1} + a_{2} < a_{1} + a_{2} < \dots < a_{1} + a_{n} < a_{2} + a_{n} < \dots < a_{n} + a_{n},

so $| A + A | \geq 2 | A | - 1$ . But we could also have written

a_{1} + a_{1} < a_{1} + a_{2} < a_{2} + a_{2} < a_{2} + a_{3} < a_{2} + a_{4} < \dots < a_{2} + a_{n} < a_{3} + a_{n} < \dots < a_{n} + a_{n} .

When $| A + A | = 2 | A | - 1$ , these two orderings must be the same. So $a_{2} + a_{i} = a_{1} + a_{i + 1}$ for all $i = 2, \dots, n - 1$ . □

Exercise: If $A, B \subseteq ℤ$ , then $| A + B | \geq | A | + | B | - 1$ with equality if and only if $A$ and $B$ are arithmetic progressions with the same common difference.

Example 1.4. Let $A, B \subseteq ℤ ∕ p ℤ$ with $p$ prime. Then $| A + B | \geq p + 1 ⟹ A + B = ℤ ∕ p ℤ$ . Indeed, $g \in A + B ⟺ A \cap (g - B) \neq \emptyset$ (note that $g - B$ means ${g} - B$ ). But $\forall g \in ℤ ∕ p ℤ$ ,

| A \cap (g - B) | = | A | + | g - B | - | A \cup (g - B) | \geq | A | + | B | - p \geq 1 .

Theorem 1.5 (Cauchy-Davenport). Assuming that:

$p$ is a prime
$A, B \subseteq ℤ ∕ p ℤ$ nonempty

Then

| A + B | \geq \min {p, | A | + | B | - 1} .

Proof. Assume $| A | + | B | \leq p + 1$ . Without loss of generality assume that $1 \leq | A | \leq | B |$ and that $0 \in A$ . Apply induction on $| A |$ . The case $| A | = 1$ is trivial. Suppose $| A | \geq 2$ , and let $0 \neq a \in A$ .

Since ${a, 2 a, 3 a, \dots, (p - 1) a, p a} = ℤ ∕ p ℤ$ and $| A | + | B | \leq p + 1$ , there must exist $m \geq 0$ such that $m a \in B$ but $(m + 1) a \notin B$ . Let $B^{'} = B - m a$ , so $0 \in B^{'}$ , $a \notin B^{'}$ , $| B^{'} | = | B |$ .

But $1 \leq | A \cap B^{'} | < | A |$ , so the inductive hypothesis applies to $A \cap B^{'}$ and $A \cup B^{'}$ . Since

(A \cap B^{'}) + (A \cup B^{'}) \subseteq A + B^{'},

we have

| A + B | = | A + B^{'} | \geq | (A \cap B^{'}) + (A \cup B^{'}) | \geq | A \cap B^{'} | + | A \cup B^{'} | + 1 = | A | + | B | + 1 . □

This fails for general abelian groups (or even general cyclic groups).

Example 1.6. Let $p$ be (fixed, small) prime, and let $V \leq 𝔽_{p}^{n}$ be a subspace. Then $V + V = V$ , so $| V + V | = | V |$ . In fact, if $A \subseteq 𝔽_{p}^{n}$ is such that $| A + A | = | A |$ , then $A$ must be a coset of a subspace.

Example 1.7. Let $A \subseteq 𝔽_{p}^{n}$ be such that $| A + A | < \frac{3}{2} | A |$ . Then there exists $V \leq 𝔽_{p}^{n}$ a subspace such that $| V | < \frac{3}{2} | A |$ and $A$ is contained in a coset of $V$ . See Example Sheet 1.

Definition 1.8 (Ruzsa distance). Given finite sets $A, B \subseteq G$ , we define the Ruzsa distance $d (A, B)$ between $A$ and $B$ by

d (A, B) = \log \frac{| A - B |}{\sqrt{| A | | B |}}

Note that this is symmetric, but is not necessarily non-negative, so we cannot prove that it is a metric. It does, however, satisfy triangle inequality:

Lemma 1.9 (Ruzsa’s triangle inequality). Assuming that:

$A, B, C \subseteq G$ finite

Then

d (A, C) \leq d (A, B) + d (B, C) .

Proof. Observe that

| B | \cdot | A - C | \leq | A - B | \cdot | B - C | .

Indeed, writing each $d \in A - C$ as $d = a_{d} - c_{d}$ with $a_{d} \in A$ , $c_{d} \in C$ , the map

\begin{array}{l} ϕ : B \times (A - C) & \to (A - B) \times (B - C) \\ (b, d) & \mapsto (a_{d} - b, b - c_{d}) \end{array}

is injective. The triangle inequality now follows from the definition. □

Definition 1.10 (Doubling / difference constant). Given a finite $A \subseteq G$ , we write

σ (A) : = \frac{| A + A |}{| A |}

for the doubling constant of $A$ and

δ (A) : = \frac{| A - A |}{| A |}

for the difference constant of $A$ .

Then Lemma 1.9 shows, for example, that

\log δ (A) = d (A, A) \leq d (A, - A) + d (- A, A) = 2 \log σ (A) .

So $δ (A) \leq σ {(A)}^{2}$ , or $| A - A | \leq \frac{| A + A |^{2}}{| A |}$ .

Notation. Given $A \subseteq G$ and $l, m \in ℕ_{0}$ , we write

l A - m A : = \underset{l times}{\underset{⏟}{A + A + \dots + A}} - \underset{m times}{\underset{⏟}{A - A - \dots - A}} .

Theorem 1.11 (Plunnecke’s Inequality). Assuming that:

$A, B \subseteq G$ are finite sets
$| A + B | \leq K | A |$ for some $K \geq 1$

Then

\forall l, m \in ℕ_{0}

| l B - m B | \leq K^{l + m} | A | .

Proof. Choose a non-empty subset $A^{'} \subseteq A$ such that the ratio $\frac{| A^{'} + B |}{| A^{'} |}$ is minimised, and call this ratio $K^{'}$ . Then $| A^{'} + B | = K^{'} | A^{'} |$ , $K^{'} \leq K$ , and $\forall A^{″} \subseteq A$ , $| A^{″} + B | \geq K^{'} | A^{″} |$ .

Claim: For every finite $C \subseteq G$ , $| A^{'} + B + C | \leq K^{'} | A^{'} + C |$ .

Let’s complete the proof of the theorem assuming the claim. We first show that $\forall m \in ℕ_{0}$ , $| A^{'} + m B | \leq {K^{'}}^{m} | A^{'} |$ . Indeed, the case $m = 0$ is trivial, and $m = 1$ is true by assumption. Suppose $m > 1$ and the inequality holds for $m - 1$ . By the claim with $C = (m - 1) B$ , we get

| A^{'} + m B | = | A^{'} + B + (m - 1) B | \leq K^{'} | A^{'} + (m - 1) B | \leq {K^{'}}^{m} | A^{'} | .

But as in the proof of Ruzsa’s triangle inequality, $\forall l, m \in ℕ_{0}$ , we can show

| A^{'} | | l B - m B | \leq | A^{'} + l B | | A^{'} + m B | \leq {K^{'}}^{l} | A^{'} | {K^{'}}^{m} | A^{'} | = {K^{'}}^{l + m} | A^{'} |^{2} .

Hence $| l B - m B | \leq {K^{'}}^{l + m} | A^{'} | \leq {K^{'}}^{l + m} | A |$ , which completes the proof (assuming the claim).

We now prove the claim by induction on $| C |$ . When $| C | = 1$ the statement follows from the assumptions. Suppose the claim is true for $C$ , and consider $C^{'} = C \cup {x}$ for some $x \notin C$ . Observe that

A^{'} + B + C^{'} = (A^{'} + B + C) + ((A^{'} + B + x) ∖ (D + B + x))

with $D = {a \in A^{'} : a + B + x \subseteq A^{'} + B + X}$ .

By definition of $K^{'}$ , $| D + B | \geq K^{'} | D |$ , so

\begin{array}{l} | A^{'} + B + C^{'} | & \leq | A^{'} + B + C | + | A^{'} + B + x | - | D + B + x | \\ \overset{IH}{\leq} K^{'} | A^{'} + C | + K^{'} | A^{'} | - K^{'} | D | \\ = K^{'} (| A^{'} + C | + | A^{'} | - | D |) \end{array}

We apply this argument a second time, writing

A^{'} + C^{'} = (A^{'} + C) ⊔ ((A^{'} + x) ∖ (E + x))

where $E = {a \in A^{'} : a + x \in A^{'} + C} \subseteq D$ . We conclude that

| A^{'} + C^{'} | = | A^{'} + C | + | A^{'} + x | - | E + x | \geq | A^{'} + C | + | A^{'} | - | D |

| A^{'} + B + C^{'} | \leq K^{'} (| A^{'} + C | + | A^{'} | - | D |) \leq K^{'} | A^{'} + C^{'} |,

proving the claim. □

We are now in a position to generalise Example 1.7.

Theorem 1.12 (Freiman-Ruzsa). Assuming that:

$A \subseteq 𝔽_{p}^{n}$
$| A + A | \leq K | A |$ (i.e. $σ (A) \leq K$ )

Then

A

is contained in a subspace

H \leq 𝔽_{p}^{n}

of size

| H | \leq K^{2} p^{K^{4}} | A |

Proof. Choose $X \subseteq 2 A - A$ maximal such that the translates $x + A$ with $x \in X$ are disjoint. Such a set $X$ cannot be too large: $\forall x \in X$ , $x + A \subseteq 3 A - A$ , so by Plunnecke’s Inequality, since $| 3 A - A | \leq K^{4} | A |$ ,

| X | | A | = | ⋃_{x \in X} (x + A) | \leq | 3 A - A | .

So $| X | \leq K^{4}$ . We next show

2 A - A \subseteq X + A - A . (∗)

Indeed, if $y \in 2 A - A$ and $y \notin X$ , then by maximality of $X$ , $y + A \cap x + A \neq \emptyset$ for some $x \in X$ (and if $y \in X$ , then clearly $y \in X + A - A$ ).

It follows from ( $*$ ) by induction that $\forall l \geq 2$ ,

l A - A \subseteq (l - 1) X + A - A, (∗∗)

since

l A - A = A + \underset{\subseteq (l - 2) X + A - A}{\underset{⏟}{(l - 1) A - A}} \subseteq (l - 2) X + \underset{⏟}{2 A - A} \subseteq X + A - A \subseteq (l - 1) X + A - A .

Now let $H \leq 𝔽_{p}^{n}$ be the subgroup generated by $A$ , which we can write as

H = ⋃_{l \geq 1} (l A - A) \overset{(* *)}{\subseteq} Y + A - A

where $Y \leq 𝔽_{p}^{n}$ is the subgroup generated by $X$ .

But every element of $Y$ can be written as a sum of $| X |$ elements of $X$ with coefficients amongst $0, 1, \dots, p - 1$ , hence $| Y | \leq p^{| X |} \leq p^{K^{4}}$ . To conclude, note that

| U | \leq | Y | | A - A | \leq p^{K^{4}} \leq p^{K^{4}} K^{2} | A |,

where we use Plunnecke’s Inequality or even Ruzsa’s triangle inequality. □

Example 1.13. Let $A = V \cup R$ where $V \leq 𝔽_{p}^{n}$ is a subspace of dimension $K ≪ d ≪ n - K$ and $R$ consists of $K - 1$ linearly independent vectors not in $V$ .

Then

| A | = | V \cup R | = | V | + | R | = p^{n ∕ k} + K - 1 \sim p^{n ∕ k} = | V |

and

| A + A | = | (V \cup R) + (V \cup R) | = | V \cup (V + R) \cup (R + R) | \sim K | V | .

But any subspace $K \leq 𝔽_{p}^{n}$ containing $A$ must have size at least $p^{n ∕ K + (K - 1)} \sim | V | \cdot p^{K}$ , so the exponential dependence on $K$ is necessary.

Theorem 1.14 (Polynomial Freiman-Ruzsa, due to Gowers–Green–Manners–Tao 2024). Assuming that:

$A \subseteq 𝔽_{p}^{n}$
$| A + A | \leq K | A |$

Then there exists a subspace

K \leq 𝔽_{p}^{n}

of size at most

C_{1} (K) | A |

such that for some

x \in 𝔽_{p}^{n}

| A \cap (x + K) | \geq \frac{| A |}{C_{2} (K)},

where $C_{1} (K)$ and $C_{2} (K)$ are polynomial in $K$ .

Proof. Omitted, because the techniques are not relevant to other parts of the course. See Entropy Methods in Combinatorics next term. □

Definition 1.15. Given $A, B \subseteq G$ we define the additive energy between $A$ and $B$ to be

E (A, B) = | {(a, a^{'}, b, b^{'}) \in A \times A \times B \times B : a + b = a^{'} + b^{'}} | .

We refer to the quadruples $(a, a^{'}, b, b^{'})$ such that $a + b = a^{'} + b^{'}$ as additive quadruples.

Example 1.16. Let $V \leq 𝔽_{p}^{n}$ be a subspace. Then $E (V) = E (V, V) = | V |^{3}$ .

On the other hand, if $A \subseteq ℤ ∕ p ℤ$ is chosen at random from $ℤ ∕ p ℤ$ (each element chosen independently with probability $α > 0$ ), then with high probability

E (A) = E (A, A) = α^{4} p^{3} = α | A |^{3} .

Lemma 1.17. Assuming that:

$A, B \subseteq G$
both non-empty

Then

E (A, B) \geq \frac{| A |^{2} | B |^{2}}{| A + B |} .

Proof. Define $r_{A + B} (x) = | {(a, b) \in A \times B : a + b = x} |$ (and notice that this is the same as $| A \cap (x - B) |$ ). Observe that

\begin{array}{l} E (A, B) & = | {(a, a^{'}, b, b^{'}) \in A^{2} \times B^{2} : a + b = a^{'} + b^{'}} \\ = \sum_{x \in G} r_{A + B} {(x)}^{2} \\ = \sum_{x \in A + B} r_{A + B} {(x)}^{2} \\ \geq \frac{{(\sum_{x \in A + B} r_{A + B} (x))}^{2}}{| A + B |} & by Cauchy-Schwarz \end{array}

but

\begin{array}{l} \sum_{x \in G} | A \cup (x - B) | & = \sum_{x \in G} \sum_{y \in G} 𝟙_{A} (y) 𝟙_{x - B} (y) \\ = \sum_{x \in G} \sum_{y \in G} 𝟙_{A} (y) 𝟙_{B} (x - y) \\ = | A | | B | \end{array}

(As usual, $𝟙_{A}$ here means the indicator function). □

In particular, if $| A + A | \leq K | A |$ , then

E (A) = E (A, A) \geq \frac{| A |^{4}}{| A + A |} \geq \frac{| A |^{3}}{K} .

The converse is not true.

Example 1.18. Let $G$ be your favourite (class of) abelian group(s). Then there exist constants $𝜃, η > 0$ such that for all sufficiently large $n$ , there exists $A \subseteq G$ , with $| A | \geq n$ satisfying $E (A) \geq η | A |^{3}$ and $| A + A | \geq 𝜃 | A |^{2}$ .

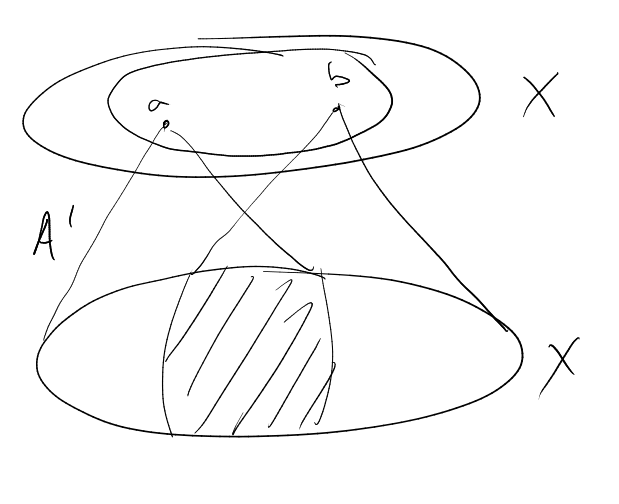
Theorem 1.19 (Balog–Szemeredi–Gowers, Schoen). Assuming that:

$A \subseteq G$ is finite
$E (A) \geq η | A |^{3}$ for some $η > 0$

Then there exists

A^{'} \subseteq A

of size at least

c_{1} (η) | A |

such that

| A^{'} + A^{'} | \leq \frac{| A^{'} |}{c_{2} (η)}

, where

c_{1} (η)

and

c_{2} (η)

are polynomial in

η

Idea: Find $A^{'} \subseteq A$ such that $\forall a, b \in A^{'}$ such that $a - b$ has many representations as $(a_{1} - a_{2}) + (a_{3} - a_{4})$ with $a_{i} \in A$ .

We first prove a technical lemma, using a technique called “dependent random choice”.

Definition 1.20 (gamma-popular differences). Given $A \subseteq G$ and $γ > 0$ , let

P_{γ} = {x \in G : | A \cap (x + A) | \geq γ | A |}

be the set of $γ$ -popular differences of $A$ .

Lemma 1.21. Assuming that:

$A \subseteq G$ is finite
$E (A) \geq η | A |^{3}$
$c > 0$

Then there is a subset

X \subseteq A

of size

| X | \geq η | A | ∕ 3

such that for all but a

(16 c)

-proportion of pairs

(a, b) \in X^{2}

a - b \in P_{c η}

Proof. Let $U = {x \in G : | A \cap (x + A) | \leq \frac{1}{2} η | A |}$ . Then

\begin{array}{l} \sum_{x \in U} | A \cap (x + A) |^{2} & = \frac{1}{2} η | A | \sum_{x} | A \cap (x + A) | \\ = \frac{1}{2} η | A |^{3} \\ = \frac{1}{2} E (A) \end{array}

For $0 \leq i \leq ⌈ \log_{2} η^{- 1} ⌉$ , let

Q_{i} = {x \in G : \frac{| A |}{2^{i + 1}} < | A \cap (x + A) | \leq \frac{| A |}{2^{i}}},

and set $δ_{i} = η^{- 1} 2^{- 2 i}$ . Then

\begin{array}{l} \sum_{i} δ_{i} | Q_{i} | & = \sum_{i} \frac{| Q_{i} |}{η^{2^{2 i}}} \\ = \frac{1}{η | A |^{2}} \sum_{i} \frac{| A |^{2}}{2^{2 i}} | Q_{i} | \\ = \frac{1}{η | A |^{2}} \sum_{i} \frac{| A |^{2}}{2^{2 i}} \sum_{x \notin U} 𝟙_{{\frac{| A |}{2^{i + 1}} < | A \cap (x + A) | \leq \frac{| A |}{2^{i}}}} \\ \geq \frac{1}{η | A |^{2}} \sum_{x \notin U} | A \cap (x + A) |^{2} \\ \geq \frac{1}{η | A |^{2}} \cdot \frac{1}{2} E (A) & (\sum_{x \in U} | A \cap (x + A) |^{2} \leq \frac{1}{2} E (A)) \\ = \frac{1}{2} | A | & (*) \end{array}

Let $S = {(a, b) \in A^{2} : a - b \notin P_{c η}}$ . Then

\begin{array}{l} \sum_{i} \sum_{(a, b) \in S} | (A - a) \cap (A - b) \cap Q_{i} | & \leq \sum_{(a, b) \in S} \underset{= \underset{by definition of S}{\underset{⏟}{| A \cap (a - b + A) | \leq c η | A |}}}{\underset{⏟}{| (A - a) \cap (A - b) |}} \\ \leq | S | \cdot c η | A | \\ \leq c η | A |^{3} \\ \leq 2 c η | A |^{2} \cdot \frac{1}{2} | A | \\ \overset{(*)}{\leq} 2 c η | A |^{2} \sum_{i} δ_{i} | Q_{i} | \end{array}

Hence there exists $i_{0}$ such that

\sum_{(a, b) \in S} | (A - a) \cap (A - b) \cap Q_{i_{0}} | \leq 2 c η | A |^{2} δ_{i_{0}} | Q_{i_{0}} | .

Let $Q = Q_{i_{0}}$ , $δ = δ_{i_{0}}$ , $λ = 2^{- i_{0}}$ . So

\sum_{(a, b) \in S} | (A - a) \cap (A - b) \cap Q | \leq 2 c η δ | A |^{2} | Q | . (∗∗)

Find $x$ such that $X = | A \cap (A + x) |$ is large.

Given $x \in G$ , let $X (x) = A \cap (x + A)$ . Then

𝔼_{x \in Q} | X (x) | = \frac{1}{| Q |} \sum_{x \in Q} | A \cap (x + A) | \geq \frac{1}{2} λ | A | .

Let $T (x) = {(a, b) \in X {(x)}^{2} : a - b \notin P_{c η}}$ . Then

\begin{array}{l} 𝔼_{X \in Q} | T (x) | & = 𝔼_{x \in Q} | {(a, b) \in {(A \cap (\underset{x \in A - a \cap A - b}{\underset{⏟}{x}} + A))}^{2} : a - b \notin P_{c η}} | \\ = \frac{1}{| Q |} \sum_{x \in Q} | {(a, b) \in S : x \in A - a \cap A - b} | \\ = \frac{1}{| Q |} \sum_{(a, b) \in S} | (A - a) \cap (A - b) \cap Q | \\ \leq \frac{1}{| Q |} 2 c η | A |^{2} δ | Q | \\ = 2 c η δ | A |^{2} \\ = 2 c λ^{2} | A |^{2} \end{array}

Therefore,

\begin{array}{l} 𝔼_{x \in Q} | X (x) |^{2} - {(16 c)}^{- 1} | T (x) | & \overset{C-S}{\leq} {(𝔼_{x \in Q} | X (x) |)}^{2} - {(16 c)}^{- 1} 𝔼_{x \in Q} | T (x) | \\ \leq {(\frac{λ}{2})}^{2} | A |^{2} - {(16 c)}^{- 1} 2 c λ^{2} | A |^{2} \\ = (\frac{λ^{2}}{4} - \frac{λ^{2}}{8}) | A |^{2} \\ = \frac{λ^{2}}{8} | A | \end{array}

So there exists $x \in Q$ such that $| X (x) |^{2} \geq \frac{λ^{2}}{8} | A |^{2}$ , in which case we have

| X | \geq \frac{λ}{\sqrt{8}} | A | \geq \frac{η}{3} | A |

and $| T (x) | \leq 16 c | X |^{2}$ . □

Proof of Theorem 1.19. Given $A \subseteq G$ with $E (A) \geq η | A |^{3}$ , apply Lemma 1.21 with $c = 2^{- 7}$ to otain $X \subseteq A$ of size $| X | \geq \frac{η}{3} | A |$ such that for all but $\frac{1}{8}$ of pairs $(a, b) \in X^{2}$ , $a - b \in P_{η ∕ 2^{7}}$ . In particular, the bipartite graph

G = (X \dot{\cup} X, {(x, y) \in X \times X : x - y \in P_{η ∕ 2^{7}}})

has at least $\frac{7}{8} | X |^{2}$ edges. Let $A^{'} = {x \in X : \deg (x) \geq \frac{3}{4} | X |}$ .

Clearly, $| A^{'} | \geq \frac{| X |}{8}$ . For any $a, b \in A^{'}$ , there are at least $\frac{| X |}{2}$ elements $y \in X$ such that $(a, y), (b, y) \in E (G)$ ( $a - y, b - y \in P_{η ∕ 2^{7}}$ ).

Thus $a - b = (a - y) - (b - y)$ has at least

\underset{choices for y}{\underset{⏟}{\frac{η}{6} | A |}} \cdot \frac{η}{2^{7}} | A | \cdot \frac{η}{2^{7}} | A | \geq \frac{η^{3}}{2^{17}} | A |^{3}

representations of the form $a_{1} - a_{2} - (a_{3} - a_{4})$ with $a_{i} \in A$ .

It follows that

\begin{array}{l} \frac{η^{3}}{2^{17}} | A |^{3} | A^{'} - A^{'} | & \leq | A |^{4} \\ ⟹ | A^{'} - A^{'} | & \leq 2^{17} η^{- 3} | A | \\ \leq 2^{22} η^{- 4} | A^{'} | \end{array}

Thus $| A^{'} + A^{'} | \leq 2^{44} η^{- 8} | A^{'} |$ . □

2 Fourier-analytic techniques

In this chapter we will assume that $G$ is finite abelian.

$G$ comes equipped with a group $Ĝ$ of characters, i.e. homomorphisms $γ : G \to ℂ$ . In fact, $Ĝ$ is isomorphic to $G$ .

See Representation Theory notes for more information about characters and proofs of this as well as some of the facts below.

Example 2.1.

(i) If $G = 𝔽_{p}^{n}$ , then for any $γ \in Ĝ = 𝔽_{p}^{n}$ , we have an associated character $γ (x) = e (γ \cdot x ∕ p)$ , where $e (y) = e^{2 π i y}$ .
(ii) If $G = ℤ ∕ N ℤ$ , then any $γ \in \hat{G} = ℤ ∕ N ℤ$ can be associated to a character $γ (x) = e (γ x ∕ N)$ .

Notation. Given $B \subseteq G$ nonempty, and any function $g : B \to ℂ$ , let

𝔼_{x \in B} g (x) = \frac{1}{| B |} \sum_{x \in B} g (x) .

Lemma 2.2. Assuming that:

$γ \in \hat{G}$

Then

𝔼_{x \in G} γ (x) = {\begin{matrix} 1 & if γ = 1 \\ 0 & otherwise \end{matrix},

and for all $x \in G$ ,

\sum_{γ \in \hat{G}} γ (x) = {\begin{matrix} | \hat{G} | & if x = 0 \\ 0 & otherwise \end{matrix} .

Proof. The first equality in eqch case is trivial. Suppose $γ \neq 1$ . Then there exists $y \in G$ with $γ (y) \neq 1$ . Then

\begin{array}{l} γ (y) 𝔼_{z \in G} γ (z) & = 𝔼_{z \in G} γ (y + z) \\ = 𝔼_{z^{'} \in G} γ (z^{'}) \end{array}

So $𝔼_{z \in G} γ (z) = 0$ .

For the second part, note that given $x \neq 0$ , there must by $γ \in \hat{G}$ such that $γ (x) \neq 1$ , for otherwise $\hat{G}$ would act trivially on $⟨ x ⟩$ , hence would also be the dual group for $G ∕ ⟨ x ⟩$ , a contradiction. □

Definition 2.3 (Fourier transform). Given $f : G \to ℂ$ , define its Fourier transform $\hat{f} : \hat{G} \to ℂ$ by

\hat{f} (γ) = 𝔼_{x \in G} f (x) \bar{γ (x)} .

It is easy to verify the inversion formula: for all $x \in G$ ,

f (x) = \sum_{γ \in \hat{G}} \hat{f} (γ) γ (x) .

Indeed,

\begin{array}{l} \sum_{γ \in \hat{G}} \hat{f} (γ) γ (x) & = \sum_{γ \in \hat{G}} 𝔼_{y \in G} f (y) \bar{γ (y)} γ (x) \\ = 𝔼_{y \in G} f (y) \underset{= | G | iff x = y}{\underset{⏟}{\sum_{γ \in \hat{G}} γ (x - y)}} \\ = f (x) & by Lemma 2.2 \end{array}

Given $A \subseteq G$ , the indicator or characteristic function of $A$ , $𝟙_{A} : G \to {0, 1}$ is defined as usual.

Note that

\hat{𝟙_{A}} (1) = 𝔼_{x \in G} 𝟙_{A} (x) 1 (x) = \frac{| A |}{| G |} .

The density of $A$ in $G$ (often denoted by $α$ ).

Definition (Characteristic measure). Given non-empty $A \subseteq G$ , the characteristic measure $μ_{A} : G \to [0, | G |]$ is defined by $μ_{A} (x) = α^{- 1} 𝟙_{A} (x)$ .

Note that $𝔼_{x \in G} μ_{A} (x) = 1 = \hat{μ_{A}} (1)$ .

Definition (Balanced function). The balanced function $f_{A} : G \to [- 1, 1]$ is given by $f_{A} (x) = 𝟙_{A} (x) - α$ . Note that $𝔼_{x \in G} f_{A} (x) = 0 = \hat{f_{A}} (1)$ .

Example 2.4. Let $V \leq 𝔽_{p}^{n}$ be a subspace. Then for $t \in \hat{𝔽_{p}^{n}}$ , we have

\begin{array}{l} \hat{𝟙_{V}} (t) & = 𝔼_{x \in 𝔽_{p}^{n}} 𝟙_{V} (x) e (- \frac{x \cdot t}{p}) \\ = \frac{| V |}{p^{n}} 𝟙_{V^{⊥}} (t) \end{array}

where $V^{⊥} = {t \in \hat{𝔽_{p}^{n}} : x \cdot t = 0 \forall x \in V}$ is the annihilator of $V$ . In other words, $\hat{𝟙_{V}} (t) = μ_{V^{⊥}} (t)$ .

Example 2.5. Let $R \subseteq G$ be such that each $x \in G$ lies in $R$ independently with probability $\frac{1}{2}$ . Then with high probability

\sup_{γ \neq 1} | \hat{𝟙_{R}} (γ) | = O (\sqrt{\frac{\log | G |}{| G |}}) .

This follows from Chernoff’s inequality: Given $ℂ$ -valued independent random variables $X_{1}, X_{2}, \dots, X_{n}$ with mean $0$ , then for all $𝜃 > 0$ , we have

ℙ (| \sum_{i = 1}^{n} X_{i} | \geq 𝜃 \sqrt{\sum_{i = 1}^{n} {∥ X_{i} ∥}_{L^{\infty} (ℙ)}^{2}}) \leq 4 \exp (- \frac{𝜃^{2}}{4}) .

Example 2.6. Let $Q = {x \in 𝔽_{p}^{n} : x \cdot x = 0} \subseteq 𝔽_{p}^{n}$ with $p > 2$ . Then

\frac{| Q |}{p^{n}} = \frac{1}{p} + O (p^{- \frac{n}{2}})

and $\sup_{t \neq 0} | \hat{𝟙_{Q}} (t) | = O (p^{- \frac{n}{2}})$ .

Given $f, g : G \to ℂ$ , we write

⟨ f, g ⟩ = 𝔼_{x \in G} f (x) \bar{g (x)} and ⟨ \hat{f}, \hat{g} ⟩ = \sum_{γ \in \hat{G}} \hat{f} (γ) \bar{\hat{g} (γ)} .

Consequently,

{∥ f ∥}_{L^{2} (G)}^{2} = 𝔼_{x \in G} | f (x) |^{2} and {∥ \hat{f} ∥}_{l^{2} (\hat{G})}^{2} = \sum_{γ \in \hat{G}} | \hat{f} (γ) |^{2} .

Lemma 2.7. Assuming that:

$f, g : G \to ℂ$

Then

(i) ${∥ f ∥}_{L^{2} (G)}^{2} = {∥ \hat{f} ∥}_{l^{2} (\hat{G})}^{2}$ (Parseval’s identity)
(ii) $⟨ f, g ⟩ = ⟨ \hat{f}, \hat{g} ⟩$ (Plancherel’s identity)

Proof. Exercise (hopefully easy). □

Definition 2.8 (Spectrum). Let $1 \geq ρ > 0$ and $f : G \to ℂ$ . Define the $ρ$ -large spectrum of $f$ to be

{Spec}_{ρ} (f) = {γ \in \hat{G} : | \hat{f} (γ) | \geq ρ {∥ f ∥}_{1}} .

Example 2.9. By Example 2.4, if $f = 𝟙_{V}$ with $V \leq 𝔽_{p}^{n}$ , then $\forall ρ > 0$ ,

{Spec}_{ρ} (𝟙_{V}) = {t \in \hat{𝔽_{p}^{n}} : | \hat{𝟙_{V}} (t) | \geq ρ \frac{| V |}{p^{n}}} = V^{⊥} .

Lemma 2.10. Assuming that:

$ρ > 0$

Then

| {Spec}_{ρ} (f) | \leq ρ^{- 2} \frac{{∥ f ∥}_{2}^{2}}{{∥ f ∥}_{1}^{2}} .

Proof. By Parseval’s identity,

\begin{array}{l} {∥ f ∥}_{2}^{2} & = {∥ \hat{f} ∥}_{2}^{2} \\ = \sum_{γ \in \hat{G}} | \hat{f} (γ) |^{2} \\ \geq \sum_{γ \in {Spec}_{ρ} (f)} | \hat{f} (γ) |^{2} \\ \geq | {Spec}_{ρ} (f) | {(ρ {∥ f ∥}_{1})}^{2} □ \end{array}

In particular, if $f = 𝟙_{A}$ for $A \subseteq G$ , then

{∥ f ∥}_{1} = α = \frac{| A |}{| G |} = {∥ f ∥}_{2}^{2},

so $| {Spec}_{ρ} (𝟙_{A}) | \leq ρ^{- 2} α^{- 1}$ .

Definition 2.11 (Convolution). Given $f, g : G \to ℂ$ , we define their convolution $f * g : G \to ℂ$ by

f * g (x) = 𝔼_{y \in G} f (y) g (x - y) \forall x \in G .

Example 2.12. Given $A, B \subseteq G$ ,

𝟙_{A} * 𝟙_{B} (x) = 𝔼_{y \in G} 𝟙_{A} (y) 𝟙_{B} (x - y) = 𝔼_{y \in G} 𝟙_{A} (y) 𝟙_{x - B} (y) = \frac{| A \cap (x - B) |}{| G |} = \frac{1}{| G |} r_{A + B} (x) .

In particular, $supp (𝟙_{A} * 𝟙_{B}) = A + B$ .

Lemma 2.13. Assuming that:

$f, g : G \to ℂ$

Then

\hat{f * g} (γ) = \hat{f} (γ) \hat{g} (γ) \forall γ \in \hat{G} .

Proof.

\begin{array}{l} \hat{f * g} (γ) & = 𝔼_{x \in G} f * g (x) \bar{γ (x)} \\ = 𝔼_{x \in G} 𝔼_{[\in y}] G f (y) g (\underset{u}{\underset{⏟}{x - y}}) \bar{γ (x)} \\ = 𝔼_{u \in G} 𝔼_{[\in y}] G f (y) g (u) \bar{γ (u + y)} \\ = \hat{f} (γ) \hat{g} (γ) □ \end{array}

Example 2.14.

𝔼_{x + y = z + w} f (x) f (y) \bar{f (z) f (w)} = ∥ \hat{f} ∥_{l^{4} (\hat{G})}^{4} .

In particular,

∥ \hat{𝟙_{A}} ∥_{l^{4} (\hat{G})}^{4} = \frac{E (A)}{| G |^{3}}

for any $A \subseteq G$ .

Theorem 2.15 (Bogolyubov’s lemma). Assuming that:

$A \subseteq 𝔽_{p}^{n}$ be a set of density $α$

Then there exists

V \leq 𝔽_{p}^{n}

of codimension

\leq 2 α^{- 2}

such that

V \subseteq A + A - A - A

Proof. Observe

2 A - 2 A = supp (\underset{= : g}{\underset{⏟}{𝟙_{A} * 𝟙_{A} * 𝟙_{- A} * 𝟙_{- A}}}),

so wish to find $V \leq 𝔽_{p}^{n}$ such that $g (x) > 0$ for all $x \in V$ . Let $S = {Spec}_{ρ} (𝟙_{A})$ with $ρ = \sqrt{\frac{α}{2}}$ and let $V = {⟨ S ⟩}^{⊥}$ . By Lemma 2.10, $codim (V) \leq | S | \leq ρ^{- 2} α^{- 1}$ . Fix $x \in V$ .

\begin{array}{l} g (x) & = \sum_{t \in \hat{𝔽_{p}^{n}}} \hat{g} (t) e (x \cdot t ∕ p) \\ = \sum_{t \in \hat{𝔽_{p}^{n}}} | \hat{𝟙_{A}} (t) |^{4} e (x \cdot t ∕ p) & by Lemma 2.13 \\ = α^{4} + \sum_{t \neq 0} | \hat{𝟙_{A}} (t) |^{4} e (x \cdot t ∕ p) \\ = α^{4} + \underset{(1)}{\underset{⏟}{\sum_{t \in S ∖ {0}} | \hat{𝟙_{A}} (t) |^{4} e (x \cdot t ∕ p)}} + \underset{(2)}{\underset{⏟}{\sum_{t \notin S} | \hat{𝟙_{A}} (t) |^{4} e (x \cdot t ∕ p)}} \end{array}

Note $(1) \geq {(ρ α)}^{4}$ since $x \cdot t = 0$ for all $t \in S$ and

\begin{array}{l} | (2) | & \leq \sup_{t \notin S} | \hat{𝟙_{A}} (t) |^{2} \sum_{t \notin S} | \hat{𝟙_{A}} |^{2} \\ \leq \sup_{t \in S} | \hat{𝟙_{A}} (t) |^{2} \sum_{t \notin S} | \hat{𝟙_{A}} |^{2} \\ \leq {(ρ α)}^{2} ∥ 𝟙_{A} ∥_{2}^{2} & by Parseval’s identity \\ = ρ^{2} α^{3} \end{array}

hence $g (x) > 0$ (in fact, $\geq \frac{α^{4}}{2}$ ) for all $x \in V$ and $codim (V) \leq 2 α^{- 2}$ . □

Example 2.16. The set $A = {x \in 𝔽_{2}^{n} : | x | \geq \frac{n}{2} + \frac{\sqrt{n}}{2}}$ (where $| x |$ counts the number of 1s in $x$ ) has density $\geq \frac{1}{8}$ , but there is no coset $C$ of any subspace of codimension $\sqrt{n}$ such that $C \subseteq A + A (= A - A)$ .

Lemma 2.17. Assuming that:

$A \subseteq 𝔽_{p}^{n}$ of density $α$
$ρ > 0$
$\sup_{t \neq 0} | \hat{𝟙_{A}} (t) | \geq ρ α$

Then there exists

V \leq 𝔽_{p}^{n}

of codimension

1

and

x \in 𝔽_{p}^{n}

such that

| A \cap (x + V) | \geq α (1 + \frac{ρ}{2}) | V | .

Proof. Let $t \neq 0$ be such that $| \hat{𝟙_{A}} (t) | \geq ρ α$ , and let $V = {⟨ t ⟩}^{⊥}$ . Write $v_{j} + V$ for $j \in [p] = {1, 2, \dots, p}$ for the $p$ distinct cosets $v_{j} + V = {x \in 𝔽_{p}^{n} : x \cdot t = j}$ of $V$ . Then

\begin{array}{l} \hat{𝟙_{A}} (t) & = \hat{f_{A}} (t) \\ = 𝔼_{x \in 𝔽_{p}^{n}} (𝟙_{A} (x) - α) e (- x \cdot t ∕ p) \\ = 𝔼_{j \in [p]} 𝔼_{x \in v_{j} + V} (𝟙_{A} (x) - α) e (- j ∕ p) \\ = 𝔼_{j \in [p]} (\underset{= a_{j}}{\underset{⏟}{\frac{| A \cap (v_{j} + V) |}{| v_{j} + V |} - α}}) e (- j ∕ p) \end{array}

By triangle inequality, $𝔼_{j \in [p]} | a_{j} | \geq ρ α$ . But note that $𝔼_{j \in [p]} a_{j} = 0$ so $𝔼_{j \in [p]} a_{j} + | a_{j} | \geq ρ α$ , hence there exists $j \in [p]$ such that $a_{j} + | a_{j} | \geq ρ α$ . Then $a_{j} \geq \frac{ρ α}{2}$ . □

Notation. Given $f, g, h : G \to ℂ$ , write

T_{3} (f, g, h) = 𝔼_{x, d \in G} f (x) g (x + d) h (x + 2 d) .

Notation. Given $A \subseteq G$ , write

2 \cdot A = {2 a : a \in A},

to be distinguished from $2 A = A + A = {a + a^{'} : a, a^{'} \in A}$ .

Lemma 2.18. Assuming that:

$p \geq 3$ prime
$A \subseteq 𝔽_{p}^{n}$ of density $α > 0$
$\sup_{t \neq 0} | \hat{𝟙_{A}} (t) | \leq 𝜀$

Then the number of 3-term arithmetic progressions in

A

differs from

α^{3} {(p^{n})}^{2}

by at most

𝜀 {(p^{n})}^{2}

Proof. The number of 3-term arithmetic progressions in $A$ is ${(p^{n})}^{2}$ times

\begin{array}{l} T_{3} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}) & = 𝔼_{x, d \in 𝔽_{p}^{n}} 𝟙_{A} (x) 𝟙_{(} x + d) 𝟙_{A} (x + 2 d) \\ = 𝔼_{x, y \in 𝔽_{p}^{n}} 𝟙_{A} (x) 𝟙_{A} (y) 𝟙_{A} (2 y - x) \\ = 𝔼_{y \in G} 𝟙_{A} (y) 𝔼_{x \in G} 𝟙_{A} (x) 𝟙_{A} (2 y - x) \\ = 𝔼_{y \in G} 𝟙_{A} (y) 𝟙_{A} * 𝟙_{A} (2 y) \\ = ⟨ 𝟙_{2 \cdot A}, 𝟙_{A} * 𝟙_{A} ⟩ \end{array}

By Plancherel’s identity and Lemma 2.13, we have

\begin{array}{l} = ⟨ \hat{𝟙_{2 \cdot A}}, {\hat{𝟙_{A}}}^{2} ⟩ \\ = \sum_{t} \hat{𝟙_{2 \cdot A}} (t) \bar{\hat{𝟙_{A}} {(t)}^{2}} \\ = α^{3} + \sum_{t \neq 0} \hat{𝟙_{2 \cdot A}} (t) \bar{\hat{𝟙_{A}} {(t)}^{2}} \end{array}

but

\begin{array}{l} | \sum_{t \neq 0} \hat{𝟙_{2 \cdot A}} (t) \hat{𝟙_{A}} {(t)}^{2} | & \leq \sup_{t \neq 0} | \hat{𝟙_{A}} (t) | \sum_{t \neq 0} | \hat{𝟙_{2 \cdot A}} (t) | | \hat{𝟙_{A}} (t) | \\ \overset{CS}{\leq} \sup_{t \neq 0} | \hat{𝟙_{A}} (t) | {(\sum_{t} | \hat{𝟙_{2 \cdot A}} (t) |^{2} \sum_{t} | \hat{𝟙_{A}} (t) |^{2})}^{\frac{1}{2}} \\ \leq 𝜀 ∥ \hat{𝟙_{2 \cdot A}} ∥_{2} ∥ \hat{𝟙_{A}} ∥_{2} \\ = 𝜀 \cdot α \end{array}

by Parseval’s identity. □

Theorem 2.19 (Meshulam’s Theorem). Assuming that:

$A \subseteq 𝔽_{p}^{n}$ a set containing no non-trivial 3 term arithmetic progressions

Then

| A | = O (\frac{p^{n}}{\log p^{n}})

Proof. By assumption,

T_{3} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}) = \frac{| A |}{{(p^{n})}^{2}} = \frac{α}{p^{n}} .

But as in (the proof of) Lemma 2.18,

| T_{3} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}) - α^{3} | \leq \sup_{t \neq 0} | \hat{𝟙_{A}} (t) | \cdot α,

so provided $p^{n} \geq 2 α^{- 2}$ , i.e. $T_{3} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}) \leq \frac{α^{3}}{2}$ we have $\sup_{t \neq 0} | \hat{𝟙_{A}} (t) | \geq \frac{α^{2}}{2}$ .

So by Lemma 2.17 with $ρ = \frac{α}{2}$ , there exists $V \leq 𝔽_{p}^{n}$ of codimension 1 and $x \in 𝔽_{p}^{n}$ such that $| A \cap (x + V) | \geq (α + \frac{α^{2}}{4}) | V |$ .

We iterate this observation: let $A_{0} = A$ , $V_{0} = 𝔽_{p}^{n}$ , $α_{0} = \frac{| A_{0} |}{| V_{0} |}$ . At the $i$ -th step, we are given a set $A_{i - 1} \subseteq V_{i - 1}$ of density $α_{i - 1}$ with no non-trivial 3 term arithmetic progressions. Provided that $p^{\dim (V_{i - 1})} \geq 2 α_{i - 1}^{- 2}$ , there exists $V_{i} \leq V_{i - 1}$ of codimension $1$ , $x_{i} \in V_{i - 1}$ such that

| (A - x_{i}) \cap V_{i} | \geq (α_{i - 1} + \frac{{(α_{i - 1})}^{2}}{4}) | V_{i} | .

Set $A_{i} = (A - x_{i}) \cap V_{i} \subseteq V_{i}$ , has density $\geq α_{i - 1} + \frac{{(α_{i - 1})}^{2}}{4}$ , and is free of non-trivial 3 term arithmetic progressions.

Through this iteration, the density increases from $α$ to $2 α$ in at most $\frac{α}{(\frac{α^{2}}{4})} = 4 \cdot α^{- 1}$ steps.

$2 α$ to $4 α$ in at most $\frac{2 α}{(\frac{{(2 α)}^{2}}{4})} = 2 α^{- 1}$ steps and so on.

So reaches $1$ in at most

4 α^{- 1} (1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots) \leq 8 α^{- 1}

steps. The argument must end with $\dim (V_{i}) \geq n - 8 α^{- 1}$ , at which point we must have had $p^{\dim (V_{i})} < 2 α_{i - 1}^{2} \leq 2 α^{- 2}$ , or else we could have continued.

But we may assume that $α \geq \sqrt{2} p^{- \frac{n}{4}}$ (or $α^{- 2} < 2 p^{\frac{n}{2}}$ ) whence $p^{n - 8 α^{- 1}} \leq p^{\frac{n}{2}}$ , or $\frac{n}{2} \leq 2 α^{- 1}$ . □

At the time of writing, the largest known subset of $𝔽_{3}^{n}$ containing no non-trivial 3 term arithmetic progressions has size ${(2.2202)}^{n}$ .

We will prove an upper bound of the form ${(2.756)}^{n}$ .

Theorem 2.20 (Roth’s theorem). Assuming that:

$A \subseteq [N] = {1, \dots, N}$
$A$ contains no non-trivial 3 term arithmetic progressions

Then

| A | = O (\frac{N}{\log \log N})

Example 2.21 (Behrend’s example). There exists $A \subseteq [N]$ of size at least $| A | \geq \exp (- c \sqrt{\log N}) N$ containing no non-trivial 3 term arithmetic progressions.

Lemma 2.22. Assuming that:

$A \subseteq [N]$ of density $α > 0$
$N > 50 α^{- 2}$
$A$ contains no non-trivial 3 term arithmetic progressions
$p$ a prime in $[\frac{N}{3}, \frac{2 N}{3}]$
let $A^{'} = A \cap [p] \subseteq ℤ ∕ p ℤ$

Then one of the following holds:

(i) $\sup_{t \neq 0} | \hat{𝟙_{A^{'}}} (t) | \geq \frac{α^{2}}{10}$ (where the Fourier coefficient is computed in $ℤ ∕ p ℤ$ )
(ii) There exists an interval $J \subseteq [N]$ of length $\geq \frac{N}{3}$ such that $| A \cap J | \geq α (1 + \frac{α}{400}) | J |$

Proof. We may assume that $| A^{'} | = | A \cap [p] | \geq α (1 - \frac{α}{200}) p$ since otherwise

\begin{array}{l} | A \cap [p + 1, N] | & \geq α N - (α (1 - \frac{α}{200}) p) \\ = α (N - p) + \frac{α^{2}}{200} p \\ \geq (α + \frac{α^{2}}{400}) (N - p) \end{array}

so we would be in Case (ii) with $J = [p + 1, N]$ . Let $A^{″} = A^{'} \cap [\frac{p}{3}, \frac{2 p}{3}]$ . Note that all 3 term arithmetic progressions of the form $(x, x + d, x + 2 d) \in A^{'} \times A^{″} \times A^{″}$ are in fact arithmetic progressions in $[N]$ .

If $| A^{'} \cap [\frac{p}{3}] |$ or $| A^{'} \cap [\frac{2 p}{3}, p] |$ were at least $\frac{2}{5} | A^{'} |$ , we would again be in case (ii). So we may assume that $| A^{″} | \geq \frac{| A^{'} |}{5}$ .

Now as in Lemma 2.18 and Theorem 2.19,

\begin{array}{l} \frac{α^{″}}{p} & = \frac{| A^{″} |}{p^{2}} \\ T_{3} (𝟙_{A^{'}}, 𝟙_{A^{″}}, 𝟙_{A^{″}}) \\ = α^{'} {(α^{″})}^{2} + \sum_{t} \bar{\hat{𝟙_{A^{'}}} (t) \hat{𝟙_{A^{″}}} (t)} \hat{𝟙_{2 \cdot A^{″}}} (t) \end{array}

where $α^{'} = \frac{| A^{'} |}{p}$ and $α^{″} = \frac{| A^{″} |}{p}$ . So as before,

\frac{α^{'} α^{″}}{2} \leq \sup_{t \neq 0} | 𝟙_{A^{'}} (t) | \cdot α^{″},

provided that $\frac{α^{″}}{p} \leq \frac{1}{2} α^{'} {(α^{″})}^{2}$ , i.e. $\frac{2}{p} \leq α^{'} α^{″}$ . (Check this is satisfied).

Hence

\sup_{t \neq 0} | \hat{𝟙_{A^{'}}} (t) | \geq \frac{α^{'} α^{″}}{2} \geq \frac{1}{2} {(α (1 - \frac{α}{200}))}^{2} \cdot \frac{2}{5} \geq \frac{α^{2}}{10} . □

Lemma 2.23. Assuming that:

$m \in ℕ$
$φ : [m] \to ℤ ∕ p ℤ$ be given by $x \mapsto t x$ for some $t \neq 0$
$𝜀 > 0$

Then there exists a partition of

[m]

into progressions

P_{i}

of length

l_{i} \in [\frac{𝜀 \sqrt{m}}{2}, 𝜀 \sqrt{m}]

such that

diam (φ (P_{i})) = \max_{x, y \in P_{i}} | φ (x) - φ (y) | \leq 𝜀 p

for all $i$ .

Proof. Let $u = ⌊ \sqrt{m} ⌋$ and consider $0, t, 2 t, \dots, u t$ . By Pigeonhole, there exists $0 \leq v < w \leq u$ such that $| w t - v t | = | (w - v) t | \leq \frac{p}{u}$ . Set $s = w - v$ , so $| s t | \leq \frac{p}{u}$ . Divide $[m]$ into residue classes modulo $s$ , each of which has size at least $\frac{m}{s} \geq \frac{m}{4}$ . But each residue class can be divided into arithmetic progressions of the form $a, a + s, \dots, a + d s$ with $𝜀 \frac{u}{2} < d \leq 𝜀 u$ . The diameter of the image of each progression under $φ$ is $| d s t | \leq d \frac{p}{u} \leq 𝜀 u \frac{p}{u} = 𝜀 p$ . □

Lemma 2.24. Assuming that:

$A \subseteq [N]$ of density $α > 0$
$p$ a prime in $[\frac{N}{3}, \frac{2 N}{3}]$
let $A^{'} = A \cap [p] \subseteq ℤ ∕ p ℤ$
$| \hat{𝟙_{A^{'}}} (t) | \geq \frac{α^{2}}{20}$ for some $t \neq 0$

Then there exists a progression

P \subseteq [N]

of length at least

α^{2} \frac{\sqrt{N}}{500}

such that

| A \cap P | \geq α (1 + \frac{α}{80}) | P |

Proof. Let $𝜀 = \frac{α^{2}}{40 π}$ , and use Lemma 2.23 to partition $[p]$ into progressions $P_{i}$ of length

\geq 𝜀 \sqrt{\frac{p}{2}} \geq \frac{α^{2}}{40 π} \frac{\sqrt{\frac{N}{3}}}{2} \geq \frac{α^{2} \sqrt{N}}{500}

and $diam (φ (P_{i})) \leq 𝜀 p$ . Fix one $x_{i}$ from each of the $P_{i}$ . Then

\begin{array}{l} \frac{α^{2}}{20} & \leq | \hat{f_{A^{'}}} (t) | \\ = | \frac{1}{p} \sum_{i} \sum_{x \in P_{i}} f_{A^{'}} (x) e (- x t ∕ p) | \\ = \frac{1}{p} | \sum_{i} \sum_{x \in P_{i}} f_{A^{'}} (x) e (- x i t ∕ p) + \sum_{i} \sum_{x \in P_{i}} f_{A^{'}} (x) (e (- x t ∕ p) - e (- x i t ∕ p)) | \\ \leq \frac{1}{p} \sum_{i} | \sum_{x \in P_{i}} f_{A^{'}} (x) | + \frac{1}{p} \sum_{i} \sum_{x \in P_{i}} | f_{A^{'}} (x) | | \underset{\begin{array}{c} \leq 2 π 𝜀 \\ since | t (x - x_{i}) | \leq 𝜀 p \end{array}}{\underset{⏟}{e (- x t ∕ p) - e (- x i t ∕ p)}} | \end{array}

\sum_{i} | \sum_{x \in P_{i}} f_{A^{'}} (x) | \geq \frac{α^{2}}{40} p .

Since $f_{A^{'}}$ has mean zero,

\sum_{i} (| \sum_{x \in P_{i}} f_{A^{'}} (x) | + \sum_{x \in P_{i}} f_{A^{'}} (x)) \geq \frac{α^{2}}{40} p,

hence there exists $i$ such that

| \sum_{x \in P_{i}} f_{A^{'}} (x) | + \sum_{x \in P_{i}} f_{A^{'}} (x) \geq \frac{α^{2}}{80} | P_{i} |

and so

\sum_{x \in P_{i}} f_{A^{'}} (x) \geq \frac{α^{2}}{160} | P_{i} | . □

Definition 2.25 (Bohr set). Let $Γ \subseteq \hat{G}$ and $ρ > 0$ . By the Bohr set $B (Γ, ρ)$ we mean the set

B (Γ, ρ) = {x \in G : | γ (x) - 1 | < ρ \forall γ \in Γ} .

We call $| Γ |$ the rank of $B (Γ, ρ)$ , and $ρ$ its width or radius.

Example 2.26. When $G = 𝔽_{p}^{n}$ , then $B (Γ, ρ) = {⟨ Γ ⟩}^{⊥}$ for all sufficiently small $ρ$ .

Lemma 2.27. Assuming that:

$Γ \subseteq \hat{G}$ of size $d$
$ρ > 0$

Then

| B (Γ, ρ) | \geq {(\frac{ρ}{8})}^{d} | G | .

Proposition 2.28 (Bogolyubov in a general finite abelian group). Assuming that:

$A \subseteq G$ of density $α > 0$

Then there exists

Γ \subseteq \hat{G}

of size at most

2 α^{- 2}

such that

A + A - A - A \supseteq B (Γ, ρ)

Proof. Recall $𝟙_{A} * 𝟙_{A} * 𝟙_{- A} * 𝟙_{- A} (x) = \sum_{γ \in \hat{G}} | \hat{𝟙_{A}} (γ) |^{4} γ (x)$ .

Let $Γ \in {Spec}_{\sqrt{\frac{α}{2}}} (𝟙_{A})$ , and note that, for $x \in B (Γ, \frac{1}{2})$ and $γ \in Γ$ , $Re (γ (x)) > 0$ . Hence, for $x \in B (Γ, \frac{1}{2})$ ,

Re \sum_{γ \in \hat{G}} | \hat{𝟙_{A}} (γ) |^{4} γ (x) = \underset{\geq α^{4}}{\underset{⏟}{Re \sum_{γ \in Γ} | \hat{𝟙_{A}} (γ) |^{4} γ (x)}} + Re \sum_{γ \notin Γ} | \hat{𝟙_{A}} (γ) |^{4} γ (x)

and

| Re \sum_{γ \notin Γ} | \hat{𝟙_{A}} (γ) |^{4} γ (x) | \leq \sup_{γ \notin Γ} | \hat{𝟙_{A}} (γ) |^{2} \sum_{γ \notin Γ} | \hat{𝟙_{A}} (γ) |^{2} \leq {(\sqrt{\frac{α}{2}} \cdot α)}^{2} \cdot α = \frac{α^{4}}{2} . □

3 Probabilistic Tools

All probability spaces in this course will be finite.

Theorem 3.1 (Khintchine’s inequality). Assuming that:

$p \in [2, \infty)$
$X_{1}, X_{2}, \dots, X_{n}$ independent random variables
$ℙ (X_{i} = x_{i}) = \frac{1}{2} = ℙ (X_{i} = - x_{i})$

Then

{∥ \sum_{i = 1}^{n} X_{i} ∥}_{L^{p} (ℙ)} = O (p^{\frac{1}{2}} {(\sum_{i = 1}^{n} ∥ X_{i} ∥_{L^{2} (ℙ)}^{2})}^{\frac{1}{2}}) .

Proof. By nesting of norms, it suffices to prove the case $p = 2 k$ for some $k \in ℕ$ . Write $X = \sum_{i = 1}^{n} X_{i}$ , and assume $\sum_{i = 1}^{n} ∥ X_{i} ∥_{L^{\infty} (ℙ)}^{2} = 1$ . Note that in fact $\sum_{i = 1}^{n} ∥ X_{i} ∥_{L^{2} (ℙ)}^{2} = \sum_{i = 1}^{n} ∥ X_{i} ∥_{L^{\infty} (ℙ)}^{2}$ , hence $\sum_{i = 1}^{n} ∥ X_{i} ∥_{L^{2} (ℙ)}^{2} = 1$ .

By Chernoff’s inequality (Example 2.5), for all $𝜃 > 0$ we have

ℙ (| X | \geq 𝜃) \leq 4 \exp (- \frac{𝜃^{2}}{4}),

and so using the fact that $ℙ (| X | \leq t) = \int_{0}^{t} ρ_{X} (s) d s$ we have

\begin{array}{l} ∥ X ∥_{L^{2 k} (ℙ)}^{2 k} & = \int_{0}^{\infty} t^{2 k} ρ_{X} (t) d t \\ = \int_{0}^{\infty} 2 k t^{2 k - 1} ℙ (| X | \geq t) d t & integration by parts \\ \leq \underset{= : I (K)}{\underset{⏟}{\int_{0}^{\infty} 8 k t^{2 k - 1} \exp (- \frac{t^{2}}{4}) d t}} \end{array}

We shall show by induction on $k$ that $I (K) \leq 2^{2 k} \frac{{(2 k)}^{k}}{4 k}$ . Indeed, when $k = 1$ ,

\int_{0}^{\infty} t \exp (- \frac{t^{2}}{4}) d t = {[- 2 \exp (- \frac{t^{2}}{4})]}_{0}^{\infty} = 2 \leq 2 .

For $k > 1$ , integrate by parts to find that

\begin{array}{l} I (K) & = \int_{0}^{\infty} \underset{u}{\underset{⏟}{t^{2 k - 2}}} \cdot \underset{v}{\underset{⏟}{t \exp (- \frac{t^{2}}{4})}} d t \\ = {[t^{2 k - 2} \cdot (- 2 \exp (- \frac{t^{2}}{4}))]}_{0}^{\infty} - \int_{0}^{\infty} (2 k - 2) t^{2 k - 3} (- 2 \exp (- \frac{t^{2}}{4})) d t \\ = 4 (k - 1) \int_{0}^{\infty} t^{2 (k - 1) - 1} \exp (- \frac{t^{2}}{4}) d t \\ = 4 (k - 1) I (K - 1) \\ \leq 4 (k - 1) 2^{2 (k - 1)} \frac{{(2 (k - 1))}^{k - 1}}{4 (k - 1)} \\ \leq 2^{2 k} \frac{{(2 k)}^{k}}{4 k} □ \end{array}

Corollary 3.2 (Rudin’s Inequality). Let $Γ \subseteq \hat{𝔽_{2}^{n}}$ be a linearly independent set and let $p \in [2, \infty)$ . Then for any $\hat{f} \in l^{2} (Γ)$ ,

{∥ \sum_{γ \in Γ} \hat{f} (γ) γ ∥}_{L^{P} (𝔽_{2}^{n})} = O (\sqrt{p} ∥ \hat{f} ∥_{l^{2} (Γ)}) .

Corollary 3.3. Let $Γ \subseteq \hat{𝔽_{2}^{n}}$ be a linearly independent set and let $p \in (1, 2]$ . Then for all $f \in L^{p} (𝔽_{2}^{n})$ ,

∥ \hat{f} ∥_{l^{2} (Γ)} = O (\sqrt{\frac{p}{p - 1}} ∥ f ∥_{L^{p} (𝔽_{2}^{n})}) .

Proof. Let $f \in L^{p} (𝔽_{2}^{n})$ and write $g = \sum_{γ \in Γ} \hat{f} (γ) γ$ . Then

\begin{array}{l} ∥ \hat{f} ∥_{l^{2} (Γ)}^{2} & = \sum_{γ \in Γ} | \hat{f} (γ) |^{2} \\ = {⟨ \hat{f}, \hat{g} ⟩}_{l^{2} (\hat{𝔽_{2}^{n}})} \\ = {⟨ f, g ⟩}_{L^{2} (𝔽_{2}^{n})} & by Plancherel’s identity \end{array}

which is bounded above by $∥ f ∥_{L^{p} (𝔽_{2}^{n})} ∥ g ∥_{L^{p^{'}} (𝔽_{2}^{n})}$ where $\frac{1}{p} + \frac{1}{p^{'}} = 1$ , using Hölder’s inequality.

By Rudin’s Inequality,

∥ g ∥_{L^{p^{'}} (𝔽_{2}^{n})} = O (\sqrt{p^{'}} ∥ \hat{g} ∥_{l^{2} (Γ)}) = O (\sqrt{\frac{p}{p - 1}} ∥ \hat{f} ∥_{l^{2} (Γ)}) . □

Recall that given $A \subseteq 𝔽_{2}^{n}$ of density $α > 0$ , we had $| {Spec}_{ρ} (𝟙_{A}) \leq ρ^{- 2} α^{- 1}$ . This is best possible as the example of a subspace shows. However, in this case the large spectrum is highly structured.

Theorem 3.4 (Special case of Chang’s Theorem). Assuming that:

$A \subseteq 𝔽_{2}^{n}$ of density $α > 0$
$ρ > 0$

Then there exists

H \leq \hat{𝔽_{2}^{n}}

of dimension

O (ρ^{- 2} \log α^{- 1})

such that

H \supseteq {Spec}_{ρ} (𝟙_{A})

Proof. Let $Γ \subseteq {Spec}_{ρ} (𝟙_{A})$ be a maximal linearly independent set. Let $H = ⟨ {Spec}_{ρ} (𝟙_{A}) ⟩$ . Clearly $\dim (H) = | Γ |$ . By Corollary 3.3, for all $p \in (1, 2]$ ,

{(ρ α)}^{2} | Γ | \leq \sum_{γ \in Γ} | \hat{𝟙_{A}} (γ) |^{2} = ∥ \hat{𝟙_{A}} ∥_{l^{2} (Γ)}^{2} = O (\frac{p}{p - 1} ∥ 𝟙_{A} ∥_{L^{p} (𝔽_{2}^{n})}^{2}),

| Γ | = O (ρ^{- 2} α^{- 2} α^{2 ∕ p} \frac{p}{p - 1}) .

Set $p = 1 + {(\log α^{- 1})}^{- 1}$ to get $| Γ | = O (ρ^{- 2} α^{- 2} (α^{2} \cdot e^{2}) (\log α^{- 1} + 1))$ . □

Definition 3.5 (Dissociated). Let $G$ be a finite abelian group. We say $S \subseteq G$ is dissociated if $\sum_{s \in S} 𝜀_{s} s = 0$ for $𝜀 \in {- 1, 0, 1}^{| S |}$ , then $𝜀 \equiv 0$ .

Clearly, if $G = 𝔽_{2}^{n}$ , then $S \subseteq G$ is dissociated if and only if it is linearly independent.

Theorem 3.6 (Chang’s Theorem). Assuming that:

$G$ a finite abelian group
$A \subseteq G$ be of density $α > 0$
$Λ \supseteq {Spec}_{ρ} (𝟙_{A})$ is dissociated

Then

| Λ | = O (ρ^{- 2} \log α^{- 1}

We may bootstrap Khintchine’s inequality to obtain the following:

Theorem 3.7 (Marcinkiewicz-Zygmund). Assuming that:

$p \in [2, \infty)$
$X_{1}, X_{2}, \dots, X_{n} \in Ł^{p} (ℙ)$ independent random variables
$𝔼 \sum_{i = 1}^{n} X_{i} = 0$

Then

{∥ \sum_{i = 1}^{n} X_{i} ∥}_{L^{p} (ℙ)} = O (p^{\frac{1}{2}} {∥ \sum_{i = 1}^{n} | X_{i} |^{2} ∥}_{L^{p ∕ 2} (ℙ)}^{\frac{1}{2}}) .

Proof. First assume the distribution of the $X_{i}$ ’s is symmetric, i.e. $ℙ (X_{i} = a) = ℙ (X_{i} = - a)$ for all $a \in ℝ$ . Partition the probability space $Ω$ into sets $Ω_{1}, Ω_{2}, \dots, Ω_{M}$ , write $ℙ_{j}$ for the induced measure on $Ω_{j}$ such that all $X_{i}$ ’s are symmetric and take at most 2 values. By Khintchine’s inequality, for each $j \in [M]$ ,

\begin{array}{l} {∥ \sum_{i = 1}^{n} X_{i} ∥}_{L^{p} (ℙ_{j})}^{p} & = O (p^{p ∕ 2} {(\sum_{i = 1}^{n} ∥ X_{i} ∥_{L^{2} (ℙ_{j})}^{2})}^{p ∕ 2}) \\ = O (p^{p ∕ 2} {∥ \sum_{i = 1}^{n} | X_{i} |^{2} ∥}_{L^{p ∕ 2} (ℙ_{j})}^{p ∕ 2}) \end{array}

so summing over all $j$ and taking $p$ -th roots gives the symmetric case. Now suppose the $X_{i}$ ’s are arbitrary, and let $Y_{1}, \dots, Y_{n}$ be such that $Y_{i} \sim X_{i}$ and $X_{1}, X_{2}, \dots, X_{n}, Y_{1}, Y_{2}, \dots, Y_{n}$ are all independent. Applying the symmetric case to $X_{i} - Y_{i}$ ,

\begin{array}{l} {∥ \sum_{i = 1}^{n} (X_{i} - Y_{i}) ∥}_{L^{p} (ℙ \times ℙ)} & = O (p^{\frac{1}{2}} {∥ \sum_{i = 1}^{n} | X_{i} - Y_{i} |^{2} ∥}_{L^{p ∕ 2} (ℙ \times ℙ)}^{\frac{1}{2}}) \\ = O (p^{\frac{1}{2}} {∥ \sum_{i = 1}^{n} | X_{i} - Y_{i} |^{2} ∥}_{L^{p ∕ 2} (ℙ)}^{\frac{1}{2}}) \end{array}

But then

\begin{array}{l} {∥ \sum_{i = 1}^{n} X_{i} ∥}_{L^{p} (ℙ)} = {∥ \sum_{i = 1}^{n} X_{i} - \underset{= 0}{\underset{⏟}{𝔼^{Y} \sum_{i = 1}^{n} Y_{i}}} ∥}_{L^{p} (ℙ)}^{p} \\ = 𝔼^{X} {| \sum X_{i} - 𝔼^{Y} \sum Y_{i} |}^{p} \\ = 𝔼^{X} {| 𝔼^{Y} \sum (X_{i} - Y_{i}) |}^{p} \\ \leq 𝔼^{X} 𝔼^{Y} {| \sum (X_{i} - Y_{i}) |}^{p} & by Jensen say \\ = {∥ \sum (X_{i} - Y_{i}) ∥}_{L^{p} (ℙ \times ℙ)}^{p} \end{array}

concluding the proof. □

Theorem 3.8 (Croot-Sisask almost periodicity). Assuming that:

$G$ a finite abelian group
$𝜀 > 0$
$p \in [2, \infty)$
$A, B \subseteq G$ are such that $| A + B | \leq K | A |$
$f : G \to ℂ$

Then there exists

b \in B

and a set

X \subseteq B - b

such that

| X | \geq 2^{- 1} K^{- O (𝜀^{- 2} p)} | B |

and

∥ τ_{x} f * μ_{A} - f * μ_{A} ∥_{L^{p} (G)} \leq 𝜀 ∥ f ∥_{L^{p} (G)} \forall x \in X,

where $τ_{x} g (y) = g (y + x)$ for all $y \in G$ , and as a reminder, $μ_{A}$ is the characteristic measure of $A$ .

Proof. The main idea is to approximate

f * μ_{A} (y) = 𝔼_{x} f (y - x) μ_{A} (x) = 𝔼_{x \in A} f (y - x)

by $\frac{1}{m} \sum_{i = 1}^{m} f (y - z_{i})$ , where $z_{i}$ are sampled independently and uniformly from $A$ , and $m$ is to be chosen later.

For each $y \in G$ , define $Z_{i} (y) = τ_{- z i} f (y) - f * μ_{A} (y)$ . For each $y \in G$ , these are independent random variables with mean $0$ , so by Marcinkiewicz-Zygmund,

\begin{array}{l} {∥ \sum_{i = 1}^{m} Z_{i} (y) ∥}_{L^{p} (ℙ)}^{p} & = O (p^{p ∕ 2} {∥ \sum_{i = 1}^{m} | Z_{i} (y) |^{2} ∥}_{L^{p ∕ 2} (ℙ)}^{p ∕ 2}) \\ = O (p^{p ∕ 2} 𝔼_{(z_{1}, \dots, z_{m}) \in A^{m}} {| \sum_{i = 1}^{m} | Z_{i} (y) |^{2} |}^{p ∕ 2}) \end{array}

By Hölder with $\frac{1}{p^{'}} + \frac{2}{p} = 1$ , we get

\begin{array}{l} {| \sum_{i = 1}^{m} | Z_{i} (y) |^{2} |}^{p ∕ 2} & \leq {(\sum_{i = 1}^{m} 1^{p^{'}})}^{\frac{1}{p^{'}} \cdot \frac{p}{2}} {(\sum_{i = 1}^{m} | Z_{i} (y) |^{2 \cdot p ∕ 2})}^{\frac{2}{p} \cdot \frac{p}{2}} \\ \leq {(\sum_{i = 1}^{m} 1^{p^{'}})}^{\frac{p}{2} - 1} {(\sum_{i = 1}^{m} | Z_{i} (y) |^{2 \cdot p ∕ 2})}^{\frac{2}{p} \cdot \frac{p}{2}} \\ = m^{p ∕ 2 - 1} \sum_{i = 1}^{m} | Z_{i} (y) |^{p} \end{array}

{∥ \sum_{i = 1}^{m} Z_{i} (y) ∥}_{L^{p} (ℙ)}^{p} = O (p^{p ∕ 2} m^{p ∕ 2 - 1} 𝔼_{(z_{1}, \dots, z_{m}) \in A^{m}} \sum_{i = 1}^{m} | Z_{i} (y) |^{p}) .

Summing over all $y \in G$ , we have

𝔼_{y \in G} {∥ \sum_{i = 1}^{m} Z_{i} (y) ∥}_{L^{p} (ℙ)}^{p} = O (p^{p ∕ 2} m^{p ∕ 2 - 1} 𝔼_{(z_{1}, \dots, z_{m}) \in A^{m}} \sum_{i = 1}^{m} 𝔼_{y \in G} | Z_{i} (y) |^{p})

with

\begin{array}{l} {(𝔼_{y \in G} | Z_{i} (y) |^{p})}^{\frac{1}{p}} & = ∥ Z_{i} ∥_{L^{p} (G)} \\ = ∥ τ_{- z_{i}} f - f * μ_{A} ∥_{L^{p} (G)} \\ \leq, ∥ τ_{- z_{i}} f ∥_{L^{p} (G)} + ∥ f * μ_{A} ∥_{L^{p} (G)} \\ \leq ∥ f ∥_{L^{p} (G)} + ∥ f ∥_{L^{q} (G)} ∥ μ_{A} ∥_{L^{1} (G)} \\ \leq 2 ∥ f ∥_{L^{p} (G)} \end{array}

by Young / Hölder ( $∥ f * g ∥_{L^{r} (G)} \leq ∥ f ∥_{L^{p} (G)} ∥ g ∥_{L^{q} (G)}$ where $1 + \frac{1}{r} = \frac{1}{p} + \frac{1}{q}$ ).

So we have

𝔼_{(z_{1}, \dots, z_{m}) \in A^{m}} 𝔼_{y \in G} {| \sum_{i = 1}^{m} Z_{i} (y) |}^{p} = O (p^{p ∕ 2} m^{p ∕ 2 - 1} \sum_{i = 1}^{m} {(2 ∥ f ∥_{L^{p} (G)})}^{p}) = O ({(4 p)}^{p ∕ 2} m^{p ∕ 2} ∥ f ∥_{L^{p} (G)}^{p}) .

Choose $m = O (𝜀^{- 2} p)$ so that the RHS is at most ${(\frac{𝜀}{4} ∥ f ∥_{L^{p} (G)})}^{p}$ . whence

𝔼_{(z_{1}, \dots, z_{m}) \in A^{m}} \underset{= (*)}{\underset{⏟}{𝔼_{y \in G} {| \frac{1}{m} \sum_{i = 1}^{m} τ_{- z i} f (y) - f * μ_{A} (y) |}^{p}}} = O ({(4 p)}^{p ∕ 2} m^{p ∕ 2} ∥ f ∥_{L^{p} (G)}^{p}) = {(\frac{𝜀}{4} ∥ f ∥_{L^{p} (G)})}^{p} .

Write

L = {z = (z_{1}, \dots, z_{m}) \in A^{m} : (*) \leq {(\frac{𝜀}{2} ∥ f ∥_{L^{p} (G)})}^{p}} .

By Markov inequality, since

𝔼 (*) \leq {(\frac{𝜀}{4} ∥ f ∥_{L^{p} (G)})}^{p} = 2^{- p} {(\frac{𝜀}{2} ∥ f ∥_{L^{p} (G)})}^{p},

we have

\frac{| A^{m} ∖ L |}{| A^{m} |} = ℙ ((*) \geq {(\frac{𝜀}{2} ∥ f ∥_{L^{p} (G)})}^{p}) \leq ℙ ((*) \geq 2^{p} 𝔼 (*)) \leq 2^{- p}

so $| L | \geq (1 - \frac{1}{2^{p}}) | A |^{m} \geq \frac{1}{2} | A |^{m}$ . Let

D = {\underset{m}{\underset{⏟}{(b, b, \dots, b)}} : b \in B} .

Now $L + D \subseteq {(A + B)}^{m}$ , whence

| L + D | \leq | A + B |^{m} \leq K^{m} | A |^{m} \leq 2 K^{m} | L | .

By Lemma 1.17,

E (L, D) \geq \frac{| L |^{2} | D |^{2}}{| L + D |} \geq \frac{1}{2} K^{- m} | D |^{2} | L |

so there are at least $\frac{| D |^{2}}{2 K^{m}}$ pairs $(d_{1}, d_{2}) \in D \times D$ such that $r_{L - L} (d_{2} - d_{1}) > 0$ . In particular, there exists $b \in u b$ and $X \subseteq B - b$ of size $| X | \geq \frac{| D |}{2 K^{m}} = \frac{| B |}{2 K^{m}}$ such that for all $x \in X$ , there exists $l_{2} (x) \in L$ such that for all $i \in [m]$ , $l_{1} {(x)}_{i} - l_{2} {(x)}_{i} = x$ . But then for each $x \in X$ , by the triangle inequality,

\begin{array}{l} ∥ τ_{- x} f * μ_{A} - f * μ_{A} ∥_{L^{p} (G)} & \leq {∥ τ_{- x} f * μ_{A} - τ_{- x} (\frac{1}{m} \sum_{i = 1}^{m} τ_{- l_{2} {(x)}_{i}} f) ∥}_{L^{p} (G)} \\ + {∥ τ_{- x} (\frac{1}{m} \sum_{i = 1}^{m} τ_{- l_{2} (x_{i})} f) - f * μ_{A} ∥}_{L^{p} (G)} \\ = {∥ f * μ_{A} - \frac{1}{m} \sum_{i = 1}^{m} τ_{- l_{2} {(x)}_{i}} f ∥}_{L^{p} (G)} \\ + {∥ \frac{1}{m} \sum_{i = 1}^{m} τ_{- x - l_{2} {(x)}_{i}} f - f * μ_{A} ∥}_{L^{p} (G)} \\ \leq 2 \cdot \frac{𝜀}{2} ∥ f ∥_{L^{p} (G)} \end{array}

by definion of $L$ . □

Theorem 3.9 (Bogolyubov again, after Sanders). Assuming that:

$A \subseteq 𝔽_{p}^{n}$ of density $α > 0$

Then there exists a subspace

V \leq 𝔽_{p}^{n}

of codimension

O (\log^{4} α^{- 1})

such tht

V \subseteq A + A - A - A

Almost periodicity is also a key ingredient in recent work of Kelley and Meka, showing that any $A \subseteq [N]$ containing no non-trivial 3 term arithmetic progressions has size $| A | \leq \exp (- C \log^{\frac{1}{11}} N) N$ .

4 Further Topics

In $𝔽_{p}^{n}$ , we can do much better.

Theorem 4.1 (Ellenberg-Gijswijt, following Croot-Lev-Pach). Assuming that:

$A \subseteq 𝔽_{3}^{n}$ contains no non-trivial 3 term arithmetic progressions

Then

| A | = o {(2.756)}^{n}

Notation. Let $M_{n}$ be the set of monomials in $x_{1}, \dots, x_{2}$ whose degree in each variable is at most $2$ . Let $V_{n}$ be the vector space over $𝔽_{3}$ whose basis is $M_{n}$ . For any $d \in [0, 2 n]$ , write $M_{n}^{d}$ for the set of monomials in $M_{n}$ of (total) degree at most $d$ , and $V_{n}^{d}$ for the corresponding vector space. Set $m_{d} = \dim (V_{n}^{d}) = | M_{n}^{d} |$ .

Lemma 4.2. Assuming that:

$A \subseteq 𝔽_{3}^{n}$
$P \in V_{n}^{d}$ is a polynomial
$P (a + a^{'}) = 0$ for all $a \neq a^{'} \in A$

Then

| {a \in A : P (2 a) \neq 0} | \leq 2 m_{d ∕ 2} .

Proof. Every $P \in V_{n}^{d}$ can be written as a linear combination of monomials in $M_{n}^{d}$ , so

P (x + y) = \sum_{\begin{array}{c} m, m^{'} \in M_{n}^{d} \\ \deg (m m^{'}) \leq d \end{array}} c_{m, m^{'}} m (x) m^{'} (y)

for some coefficients $c_{m, m^{'}}$ . Clearly at least one of $m, m^{'}$ must have degree $\leq \frac{d}{2}$ , whence

P (x + y) = \sum_{m \in M_{n}^{d ∕ 2}} m (x) F_{m} (y) + \sum_{m^{'} \in M_{n}^{d ∕ 2}} m^{'} (y) G_{m^{'}} (x),

for some families of polynomials ${(F_{m})}_{m \in M_{n}^{d ∕ 2}}$ , ${(G_{m^{'}})}_{m^{'} \in M_{n}^{d ∕ 2}}$ .

Viewing ${(P (x + y))}_{x, y \in A}$ as a $| A | \times | A |$ -matrix $C$ , we see that $C$ can be written as the sum of at most $2 m_{d ∕ 2}$ matrices, each of which has rank $1$ . Thus $rank (C) \leq 2 m_{d ∕ 2}$ . But by assumption, $C$ is a diagonal matrix whose rank equals $| {a \in A : P (a + a) \neq 0} |$ . □

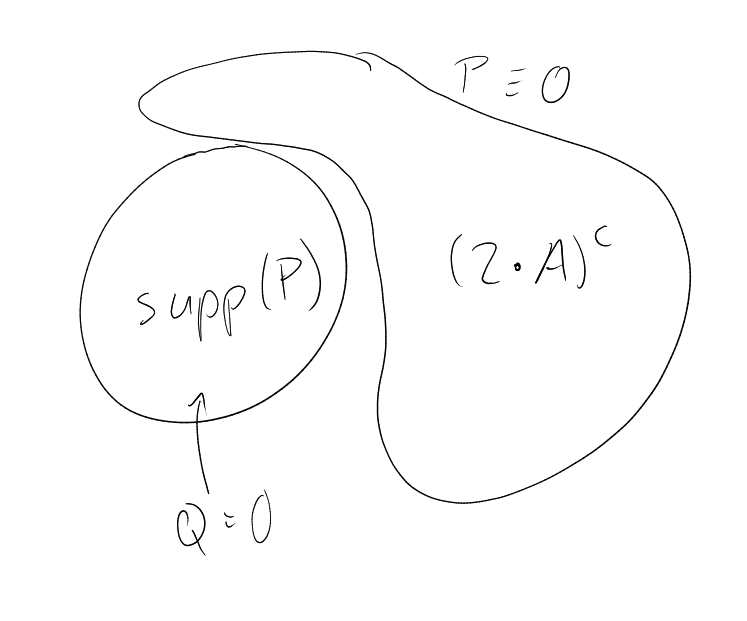
Proposition 4.3. Assuming that:

$A \subseteq 𝔽_{3}^{n}$ a set containing no non-trivial 3 term arithmetic progressions

Then

| A | \leq 3 m_{2 n ∕ 3}

Proof. Let $d \in [0, 2 n]$ be an integer to be determined later. Let $W$ be the space of polynomials in $V_{n}^{d}$ that vanish on ${(2 \cdot A)}^{c}$ . We have

\dim (W) \geq \dim (V_{n}^{d}) - | {(2 \cdot A)}^{c} | = m_{d} - (3^{n} - | A |) .

We claim that there exists $P \in W$ such that $| supp (P) | \geq \dim (W)$ . Indeed, pick $P \in W$ with maximal support. If $| supp (P) | < \dim (W)$ , then there would be a non-zero polynomial $Q \in W$ vanishing on $supp (P)$ , in which case $supp (P + Q) ⊋ supp (P)$ , contradicting the choice of $P$ .

Now by assumption,

{a + a^{'} : a \neq a^{'} \in A} \cap 2 \cdot A = \emptyset .

So any polynomial that vanishes on ${(2 \cdot A)}^{c}$ vanishes on ${a + a^{'} : a \neq a^{'} \in A}$ . By Lemma 4.2 we now have that,

\begin{array}{l} | A | - (3^{n} - m_{d}) & = m_{d} - (3^{n} - | A |) \\ \leq \dim (W) \\ \leq | supp (P) | \\ = | {x \in 𝔽_{3}^{n} : P (x) \neq 0} | \\ = | {a \in A : P (2 a) \neq 0} | \\ \leq 2 m_{d ∕ 2} \end{array}

Hence $| A | \geq 3^{n} - m_{d} + 2 m_{d ∕ 2}$ . But the monomials in $M_{n} ∖ M_{n}^{d}$ are in bijection with the ones in $M_{2 n - d}$ via $x_{1}^{α_{1}} \dots x_{n}^{α_{n}} \mapsto x_{1}^{2 - α_{1}} \dots x_{n}^{2 - α_{n}}$ , whence $3^{n} - m_{d} = m_{2 n - d}$ . Thus setting $d = \frac{4 n}{3}$ , we have $| A | \leq m_{2 n ∕ 3} + 2 m_{2 n ∕ 3} = 3 m_{2 n ∕ 3}$ . □

You will prove Theorem 4.1 on Example Sheet 3.

We do not have at present a comparable bound for 4 term arithmetic progressions. Fourier techniques also fail.

Example 4.4. Recall from Lemma 2.18 that given $A \subseteq G$ ,

| T_{3} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}) - α^{3} | \geq \sup_{γ \neq 1} | \hat{𝟙_{A}} (γ) | .

But it is impossible to bound

T_{4} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}, 𝟙_{A}) - α^{4} = 𝔼_{x \in d} 𝟙_{A} (x) 𝟙_{A} (x + d) 𝟙_{A} (x + 2 d) 𝟙_{A} (x + 3 d) - α^{4}

by $\sup_{γ \neq 1} | \hat{𝟙_{A}} (γ) |$ . Indeed, consider $Q = {x \in 𝔽_{p}^{n} : x \cdot x = 0}$ . By Problem 11(ii) on Sheet 1,

\frac{| Q |}{p^{n}} = \frac{1}{p} + O (p^{- n ∕ 2})

and

\sup_{t \neq 0} | \hat{𝟙_{Q}} (t) | = O (p^{- n ∕ 2}) .

But given a 3 term arithmetic progression $x, x + d, x + 2 d \in Q$ , by the identity

x^{2} - 3 {(x + d)}^{2} + 3 {(x + 2 d)}^{2} - {(x + 3 d)}^{2} = 0 \forall x, d,

$x + 3 d$ automatically lies in $Q$ , so

T_{4} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}, 𝟙_{A}) = T_{3} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}) = {(\frac{1}{p})}^{3} + O (p^{- n ∕ 2})

which is not close to ${(\frac{1}{p})}^{4}$ .

Definition 4.5 ( $U^{2}$ -norm). Given $f : G \to ℂ$ , define its $U^{2}$ -norm by the formula

∥ f ∥_{U^{2} (G)}^{4} = 𝔼_{x, a, b \in G} f (x) \bar{f (x + a) f (x + b)} f (x + a + b) .

Problem 1(i) on Sheet 2 showed that $∥ f ∥_{U^{2} (G)} = ∥ \hat{f} ∥_{l^{4} (\hat{G})}$ , so this is indeed a norm.

Problem 1(ii) asserted the following:

Lemma 4.6. Assuming that:

$f_{1}, f_{2}, f_{3} : G \to ℂ$

Then

| T_{3} (f_{1}, f_{2}, f_{3}) | \leq \min_{i \in [3]} ∥ f_{i} ∥_{U^{2} (G)} \cdot \prod_{j \neq i} ∥ f_{j} ∥_{L^{\infty} (G)} .

Note that

\sup_{γ \in \hat{G}} | \hat{f} (γ) |^{4} \leq \sum_{γ \in \hat{G}} | \hat{f} (γ) |^{4} \leq \sup_{γ \in \hat{G}} | \hat{f} (γ) |^{2} \sum_{γ \in \hat{G}} | \hat{f} (γ) |^{2}

and thus by Parseval’s identity,

∥ f ∥_{U^{2} (G)}^{4} = ∥ \hat{f} ∥_{l^{\infty} (\hat{G})}^{4} \leq ∥ \hat{f} ∥_{l^{\infty} (\hat{G})}^{2} ∥ f ∥_{L^{2} (G)}^{2} .

Hence

∥ \hat{f} ∥_{l^{\infty} (\hat{G})} \leq ∥ \hat{f} ∥_{l^{4} (\hat{G})} = ∥ f ∥_{U^{2} (G)} \leq ∥ \hat{f} ∥_{l^{\infty} (\hat{G})}^{\frac{1}{2}} ∥ f ∥_{L^{2} (G)}^{\frac{1}{2}} .

Moreover, if $f = f_{A} A = 𝟙_{A} - α$ , then

T_{3} (f, f, f) = T_{3} (𝟙_{A} - α, 𝟙_{A} - α, 𝟙_{A} - α) = T_{3} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}) - α^{3} .

We may therefore reformulate the first step in the proof of Meshulam’s Theorem as follows: if $p^{n} \geq 2 α^{- 2}$ , then by Lemma 4.6,

\frac{α^{3}}{2} \leq | \frac{α}{p^{n}} - α^{3} | = | T_{3} (f_{A} A, f_{A} A, f_{A} A) | \leq ∥ f_{A} A ∥_{U^{2} (𝔽_{p}^{n})} .

It remains to show that if $∥ f_{A} A ∥_{U^{2} (𝔽_{p}^{n})}$ is non-trivial, then there exists a subspace $V \leq 𝔽_{p}^{n}$ of bounded codimension on which $A$ has increased density.

Theorem 4.7 ( $U^{2}$ Inverse Theorem). Assuming that:

$f : 𝔽_{p}^{n} \to ℂ$
$∥ f ∥_{L^{\infty} (𝔽_{p}^{n})} \leq 1$
$δ > 1$
$∥ f ∥_{U^{2} (𝔽_{p}^{n})} \geq δ$

Then there exists

b \in 𝔽_{p}^{n}

such that

| 𝔼_{x \in 𝔽_{p}^{n}} f (x) e (- x \cdot b ∕ p) | \geq δ^{2} .

In other words, $| ⟨ f, ϕ ⟩ | \geq δ^{2}$ for $ϕ (x) = e (- x \cdot b ∕ p)$ and we say “ $f$ correlates with a linear phase function”.

Proof. We have seen that

∥ f ∥_{U^{2} (𝔽_{p}^{n})}^{2} \leq ∥ \hat{f} ∥_{l^{\infty} (\hat{𝔽_{p}^{n}})} ∥ f ∥_{L^{2} (𝔽_{p}^{n})} \leq ∥ \hat{f} ∥_{l^{\infty} (\hat{𝔽_{p}^{n}})},

δ^{2} \leq ∥ \hat{f} ∥_{l^{\infty} (\hat{𝔽_{p}^{n}})} = \sup_{t \in \hat{𝔽_{p}^{n}}} | 𝔼_{x} f (x) e (- x \cdot t ∕ p) | . □

Definition 4.8 ( $U^{3}$ norm). Given $f : G \to ℂ$ , define its $U^{3}$ norm by

\begin{array}{l} ∥ f ∥_{U^{3} (G)}^{8} & : = 𝔼_{_{\in} x, a, b, c} f (x) \bar{f (x + a) f (x + b) f (x + c)} \\ f (x + a + b) f (x + b + c) f (x + a + c) \bar{f (x + a + b + c)} \\ = 𝔼_{x, h_{1}, h_{2}, h_{3} \in G} \prod_{𝜀 \in {0, 1}^{3}} C^{| 𝜀 |} f (x + 𝜀 \cdot h) \end{array}

where $C g (x) = \bar{g (x)}$ and $| 𝜀 |$ denotes the number of ones in $𝜀$ .

It is easy to verify that $𝔼_{c \in G} ∥ Δ_{c} f ∥_{U^{2} (G)}^{4}$ where $Δ_{c} g (x) = g (x) \bar{g (x + c)}$ .

Definition 4.9 ( $U^{3}$ inner product). Given functions $f_{𝜀} : G \to ℂ$ for $𝜀 \in {0, 1}^{3}$ , define their $U^{3}$ inner product by

{⟨ {(f_{𝜀})}_{𝜀 \in {0, 1}^{3}} ⟩}_{U^{3} (G)} = 𝔼_{x, h_{1}, h_{2}, h_{3} \in G} \prod_{𝜀 \in {0, 1}^{3}} C^{| 𝜀 |} f_{𝜀} (x + 𝜀 \cdot h) .

Observe that ${⟨ f, f, f, f, f, f, f, f ⟩}_{U^{3} (G)} = {∥ f ∥_{U^{3} (G)}}^{8}$ .

Lemma 4.10 (Gowers–Cauchy–Schwarz Inequality). Assuming that:

$f_{𝜀} : G \to ℂ$ , $𝜀 \in {0, 1}^{3}$

Then

| {⟨ {(f_{𝜀})}_{𝜀 \in {0, 1}^{3}} ⟩}_{U^{3} (G)} \leq \prod_{𝜀 \in {0, 1}^{3}} ∥ f_{𝜀} ∥_{U^{3} (G)} .

Setting $f_{𝜀} = f$ for $𝜀 \in {0, 1}^{2} \times {0}$ and $f_{𝜀} = 1$ otherwise, it follows that $∥ f ∥_{U^{2} (G)}^{4} \leq {∥ f ∥_{U^{3} (G)}}^{4}$ hence $∥ f ∥_{U^{2} (G)} \leq ∥ f ∥_{U^{3} (G)}$ .

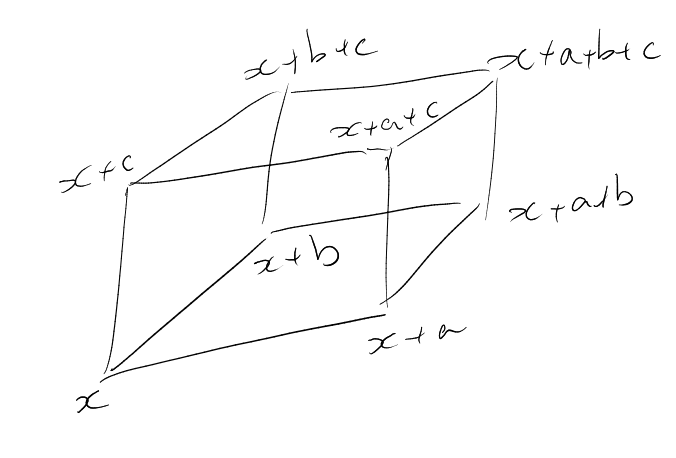
Proposition 4.11. Assuming that:

$f_{1}, f_{2}, f_{3}, f_{4} : 𝔽_{5}^{n} \to ℂ$

Then

T_{4} (f_{1}, f_{2}, f_{3}, f_{4}) \leq \min_{i \in [4]} ∥ f_{i} ∥_{U^{3} (G)} \prod_{j \neq i} ∥ f_{j} ∥_{L^{\infty} (𝔽_{5}^{n})} .

Proof. We additionally assume $f = f_{1} = f_{2} = f_{3} = f_{4}$ to make the proof easier to follow, but the same ideas are used for the general case. We additionally assume $∥ f ∥_{L^{\infty} (𝔽_{5}^{n})} \leq 1$ , by rescaling, since the inequality is homogeneous.

Reparametrising, we have

\begin{array}{l} T_{4} (f, f, f, f) & = 𝔼_{a, b, c, d \in 𝔽_{5}^{n}} f (3 a + 2 b + c) f (2 a + b - d) f (a - c - 2 d) f (- b - 2 c - 3 d) \\ | T_{4} (f, f, f, f) |^{8} & \leq (𝔼_{a, b, c} | 𝔼_{d} f (2 a + b - d) f (a - c - 2 d) f (- b - 2 c - 3 d) |^{2})^{4} \\ = (𝔼_{d, d^{'}} 𝔼_{a, b} f (2 a + b + d) \bar{f (2 a + b - d^{'})} \\ 𝔼_{c} f (a - c - 2 d) \bar{f (a - c - 2 d^{'})} f (- b - 2 c - 3 d) \bar{f (- b - 2 c - 3 d^{'})})^{4} \\ \leq (𝔼_{d, d^{'}} 𝔼_{a, b} | 𝔼_{c} f (a - c - 2 d) \bar{f (a - c - 2 d^{'})} f (- b - 2 c - 3 d) \bar{f (- b - 2 c - 3 d^{'})} |^{2})^{2} \\ = (𝔼_{c, c^{'}, d, d^{'}} 𝔼_{a} f (a - c - 2 d) \bar{f (a - c^{'} - 2 d)} \bar{f (a - c - 2 d^{'})} f (a - c^{'} - 2 d^{'}) \\ 𝔼_{b} f (- b - 2 c - 3 d) \bar{f (- b - 2 c^{'} - 3 d)} \bar{f (- b - 2 c - 3 d^{'})} f (- b - 2 c^{'} - 3 d^{'}))^{2} \\ \leq 𝔼_{c, c^{'}, d, d^{'}, a} | 𝔼_{b} f (- b - 2 c - 3 d) \bar{f (- b - 2 c^{'} - 3 d)} \bar{f (- b - 2 c - 3 d^{'})} f (- b - 2 c^{'} - 3 d^{'}) |^{2} \\ = 𝔼_{b, b^{'}, c, c^{'}, d, d^{'}} f (- b - 2 c - 3 d) \bar{f (- b^{'} - 2 c - 3 d)} \bar{f (- b - 2 c^{'} - 3 d)} f (- b^{'} - 2 c^{'} - 3 d) \\ \bar{f (- b - 2 c - 3 d^{'})} f (- b^{'} - 2 c - 3 d^{'}) f (- b - 2 c^{'} - 3 d^{'}) \bar{f (- b^{'} - 2 c^{'} - 3 d^{'})} □ \end{array}

Theorem 4.12 (Szemeredi’s Theorem for 4-APs). Assuming that:

$A \subseteq 𝔽_{5}^{n}$ a set containing no non-trivial 4 term arithmetic progressions

Then

| A | = o (5^{n})

Idea: By Proposition 4.11 with $f = f_{A} = 𝟙_{A} - α$ ,

T_{4} (\underset{f_{A} + α}{\underset{⏟}{𝟙_{A}}}, \underset{f_{A} + α}{\underset{⏟}{𝟙_{A}}}, \underset{f_{A} + α}{\underset{⏟}{𝟙_{A}}}, \underset{f_{A} + α}{\underset{⏟}{𝟙_{A}}}) - α^{4} = T_{4} (f_{A}, f_{A}, f_{A}, f_{A}) + \dots

where $\dots$ consists of $14$ other terms in which between one and three of the inputs are equal to $f_{A}$ .

These are controlled by

∥ f_{A} ∥_{U^{2} (𝔽_{5}^{n})} \leq ∥ f_{A} ∥_{U^{3} (G)},

whence

| T_{4} (𝟙_{A}, 𝟙_{A}, 𝟙_{A}, 𝟙_{A}) - α^{4} | \leq 15 ∥ f_{A} ∥_{U^{3} (G)} .

So if $A$ contains no non-trivial 4 term arithmetic progressions and $5^{n} > 2 α^{- 3}$ , then $∥ f_{A} ∥_{U^{3} (G)} \geq \frac{α^{4}}{30}$ .

What can we say about functions with large $U^{3}$ norm?

Example 4.13. Let $M$ be an $n \times n$ symmetric matrix with entries in $𝔽_{5}$ . Then $f (x) = e (x^{⊤} M x ∕ 5)$ satisfies $∥ f ∥_{U^{3} (G)} = 1$ .

Theorem 4.14 ( $U^{3}$ inverse theorem). Assuming that:

$f : 𝔽_{5}^{n} \to ℂ$
$∥ f ∥_{L^{\infty} (𝔽_{5}^{n})} \leq 1$
$∥ f ∥_{U^{3} (G)} \geq δ$ for some $δ > 0$

Then there exists a symmetric

n \times n

matrix

M

with entries in

𝔽_{5}

and

b \in 𝔽_{5}^{n}

such that

| 𝔼_{x} f (x) e ((x^{⊤} M x + b^{⊤} x) ∕ p) | \geq c (δ)

where $c (δ)$ is a polynomial in $δ$ . In other words, $| ⟨ f, ϕ ⟩ | \geq c (δ)$ for $ϕ (x) = e ((x^{⊤} M x + b^{⊤} x) ∕ p)$ and we say “ $f$ correlates with a quadratic phase function”.

Proof (sketch). Let $Δ_{h} f (x)$ denote $f (x) \bar{f (x + h)}$ .

$∥ f ∥_{U^{3} (G)} = {(𝔼_{h} ∥ Δ_{h} f ∥_{U^{2}}^{4})}^{\frac{1}{8}}$ .

STEP 1: Weak linearity. See reference.
STEP 2: Strong linearity. We will spend the rest of the lecture discussing this in detail.
STEP 3: Symmetry argument. Problem 8 on Sheet 3.
STEP 4: Integration step. Problem 9 on Sheet 3.

STEP 1: If ${∥ f ∥_{U^{3} (G)}}^{8} = 𝔼_{h} ∥ Δ_{h} ∥_{U^{2}}^{4} \geq δ^{8}$ , then for at least a $\frac{δ^{8}}{2}$ -proportion of $h \in 𝔽_{5}^{n}$ , $\frac{δ^{8}}{2} \leq ∥ Δ_{h} f ∥_{U^{2}}^{4} \leq ∥ \hat{Δ_{h} f} ∥_{l^{\infty}}^{2}$ . So for each such $h \in 𝔽_{5}^{n}$ , there exists $t_{h}$ such that $| \hat{Δ_{h} f} (t_{h}) |^{2} \geq \frac{δ^{8}}{2}$ .

Proposition 4.15. Assuming that:

$f : 𝔽_{5}^{n} \to ℂ$
$∥ f ∥_{\infty} \leq 1$
$∥ f ∥_{U^{3} (G)} \geq δ$
$| 𝔽_{5}^{n} | = Ω_{δ} (1)$

Then there exists

S \subseteq 𝔽_{5}^{n}

with

| S | = Ω_{δ} (| 𝔽_{5}^{n} |)

and a function

ϕ : S \to \hat{𝔽_{5}^{n}}

such that

(i) $| \hat{Δ_{h} f} (ϕ (h)) | = Ω_{δ} (1)$ ;
(ii) There are at least $Ω_{δ} (| 𝔽_{5}^{n} |^{3})$ quadruples $(s_{1}, s_{2}, s_{3}, s_{4}) \in S^{4}$ such that $s_{1} + s_{2} = s_{3} + s_{4}$ and $ϕ (s_{1}) + ϕ (s_{2}) + ϕ (s_{4})$ .

STEP 2: If $S$ and $ϕ$ are as above, then there is a linear function $ψ : 𝔽_{5}^{n} \to \hat{𝔽_{5}^{n}}$ which coincides with $ϕ$ for many elements of $S$ .

Proposition 4.16. Assuming that:

$S$ and $ϕ$ given as in Proposition 4.15

Then there exists

n \times n

matrix

M

with entries in

𝔽_{5}

and

b \in 𝔽_{5}^{n}

such that

ψ (x) = M x + b

(

ψ : 𝔽_{5}^{n} \to \hat{𝔽_{5}^{n}}

) satisfies

ψ (x) = ϕ (x)

for

Ω_{δ} (| 𝔽_{5}^{n} |)

elements

x \in S

Proof. Consider the graph of $ϕ$ , $Γ = {(h, ϕ (h)) : h \in S} \subseteq 𝔽_{5}^{n} \times \hat{𝔽_{5}^{n}}$ . By Proposition 4.15, $Γ$ has $Ω_{δ} (| 𝔽_{5}^{n} |^{3})$ additive quadruples.

By Balog–Szemeredi–Gowers, Schoen, there exists $Γ^{'} \subseteq Γ$ with $| Γ^{'} | = Ω_{δ} (| Γ |) = Ω_{δ} (| 𝔽_{5}^{n} |)$ and $| Γ^{'} + Γ^{'} | = O_{δ} (| Γ^{'} |)$ . udefine $S^{'} \subseteq S$ by $Γ^{'} = {(h, ϕ (h)) : h \in S^{'}}$ and note $| S^{'} | = Ω_{δ} (| 𝔽_{5}^{n} |)$ .

By Freiman-Ruzsa applied to $Γ^{'} \subseteq 𝔽_{5}^{n} \times \hat{𝔽_{5}^{n}}$ , there exists a subspace $H \leq 𝔽_{5}^{n} \times \hat{𝔽_{5}^{n}}$ with $| H | = O_{δ} (| Γ^{'} |) = O_{δ} (| 𝔽_{5}^{n} |)$ such that $Γ^{'} \subseteq H$ .

Denote by $π : 𝔽_{5}^{n} \times \hat{𝔽_{5}^{n}} \to 𝔽_{5}^{n}$ the projection onto the first $n$ coordinates. By construction, $π (H) \supseteq S^{'}$ . Moreover, since $| S^{'} | = Ω_{δ} (| 𝔽_{5}^{n} |)$ ,

| \ker (π |_{H}) | = \frac{| H |}{| Im (π |_{H}) |} = \frac{O_{δ} (| 𝔽_{5}^{n} |)}{| S^{'} |} = O_{δ} (1) .

We may thus partition $H$ into $O_{δ} (1)$ cosets of some subspace $H^{*}$ such that $π |_{H}$ is injective on each coset. By averaging, there exists a coset $x + H^{*}$ such that

| Γ^{'} \cap (x + H^{*}) | = Ω_{δ} (| Γ^{'} |) = Ω_{δ} (| 𝔽_{5}^{n} |) .

Set $Γ^{″} = Γ^{'} \cap (x + H^{*})$ , and define $S^{″}$ accordingly.

Now $π |_{x +^{*}}$ is injective and surjective onto $V : = Im (π |_{x + H^{*}})$ . This means there is an affine linear map $ψ : V \to \hat{𝔽_{5}^{n}}$ such that $(h, ψ (h)) \in Γ^{″}$ for all $h \in S^{″}$ . □