Review of First Order Logic - Model Theory

0 Review of First Order Logic

0.1 Languages

\underset{language}{\underset{⏟}{L}} = \underset{function symbols}{\underset{⏟}{F}} \cup \underset{relation symbols}{\underset{⏟}{R}} \cup \underset{constant symbols}{\underset{⏟}{C}} .

Example.

$L_{group} = {*, e}$ , with example sentences $x \cdot x = e$ , $\exists y, x \cdot y = e$ .
$L_{rings} = {+, \times, 0, 1}$ : $x^{2} + x + 1 = 0$ .
$L_{o} = {<}$ : $\forall x \forall y ((x < y \land y < x) \to x = y)$ .

Convention: all languages include $=$ .

0.2 Structures

Definition. Given a language $L$ , an $L$ -structure is a triple

M = ⟨ M, \hat{F}, \hat{R}, \hat{C} ⟩ .

$M$ is an underlying set.

Convention: $M \neq \emptyset$ .

$\hat{F}$ : for every $n$ -ary $f \in F$ we have $\hat{f} \in \hat{F}$ a function $\hat{f} : m^{n} \to m$ .

$\hat{R}$ : for every $n$ -ary $R \in R$ , we have $\hat{R} \in \hat{R}$ , which is a subset of $M^{n}$ .

$\hat{C}$ : for every $c \in C$ , we have $ĉ \in \hat{C}$ , with $ĉ \in M$ .

$⟨ ℂ, +, 0 ⟩$ and $⟨ ℂ, \times, 1 ⟩$ are both $L_{group}$ -structures.
$⟨ ℚ, < ⟩$ and $⟨ ℚ, x + y = 3 ⟩$ are both $L_{o}$ -structures.

0.3 Formulas / sentences

Terms: made of variables, constant symbols and function symbols in a ‘sensible way’
$x + y x + 1 + 1 \cdot + x | \cdot \cdot .$
Atomic formulas: Plugging terms into one relation symbol
$x + y x + 1 + 1 = 0 = = + 1 \cdot 0$
Formulas:
- Boolean combinations ( $\neg, \land, \lor, \to, \leftrightarrow$ )
- Quantifiers ( $\exists, \forall$ )
in a ‘sensible way’:
$\exists y (x + y x + 1 + 1 = 0 \lor x = 1) \forall x + \land 0 .$

A formula with $n$ free variables defines a subset of $M^{n}$ .

Example. $L_{o}$ -structure $⟨ ℚ, < ⟩$ .

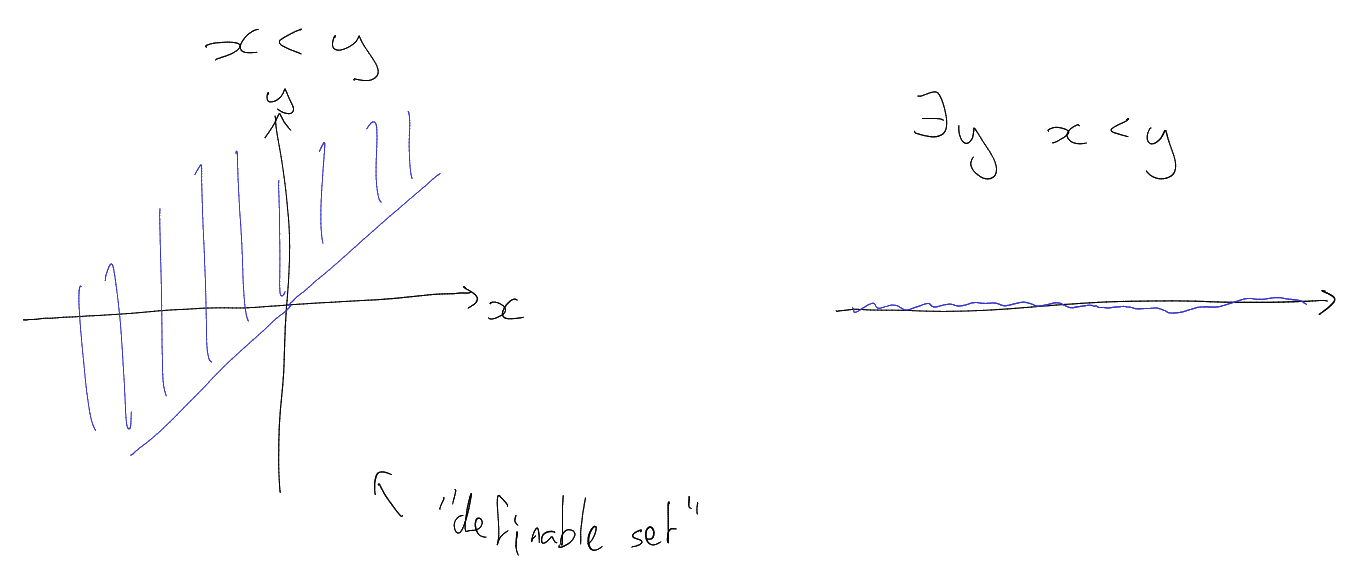
Formulas with no free variables are called sentences.

In an $L$ -structure $M$ , these are either:

True: $M ⊨ σ$
False: $M ⁄ ⊨ σ$

In formula $ϕ (\bar{x})$ with free variables, we can plug a tuple $\underset{̲}{a} \in M^{n}$ . We say $M$ satisfies $ϕ (\underset{̲}{x})$ at $\underset{̲}{a}$ , and we write $M ⊨ ϕ (\underset{̲}{a})$ (models / satisfies) if $ϕ (\underset{̲}{a})$ is true in $M$ .

Definition. A set of sentences $Σ$ is satisfiable in $M$ if for all $σ \in Σ$ , $M ⊨ σ$ .

Theorem (Compactness Theorem). Let $Σ$ be a set of $L$ -sentences. $Σ$ is satisfiable if and only if every finite subset of $Σ$ is satisfiable.

( $Σ$ is satisfiable if there is an $L$ -structure $M$ such that $Σ$ is satisfiable in $M$ )

Corollary (Upward Löwenheim Skolem). Any theory that has either:

arbitrary large finite models
at least one infinite model

has arbitrarily large models.