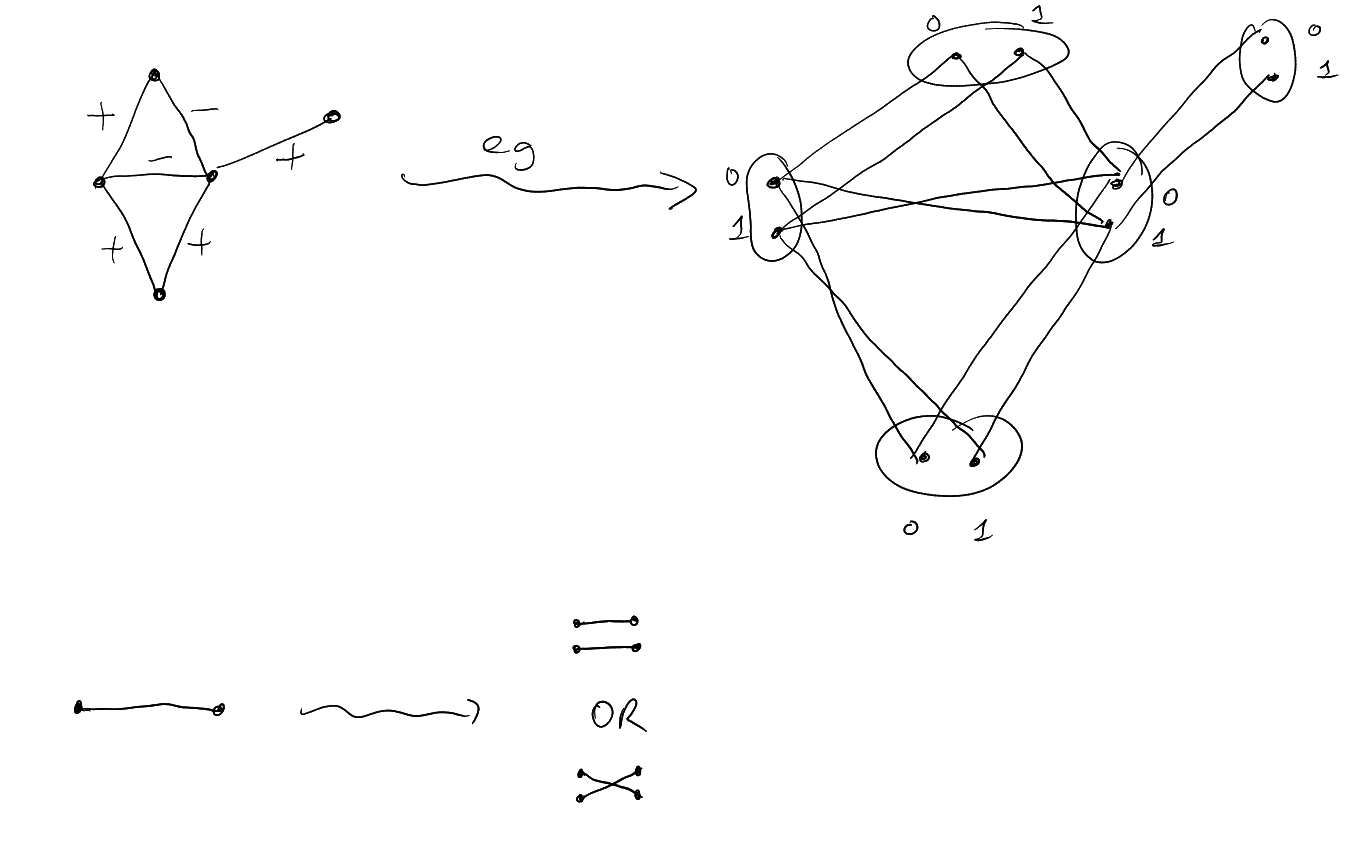
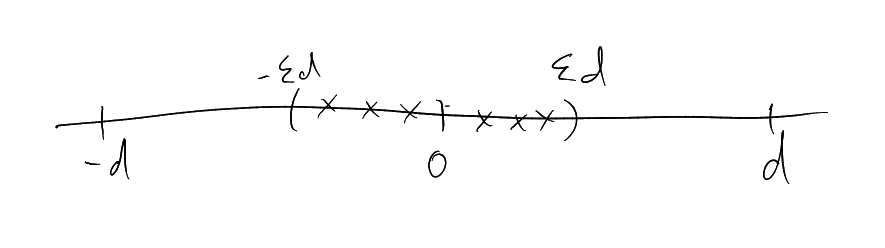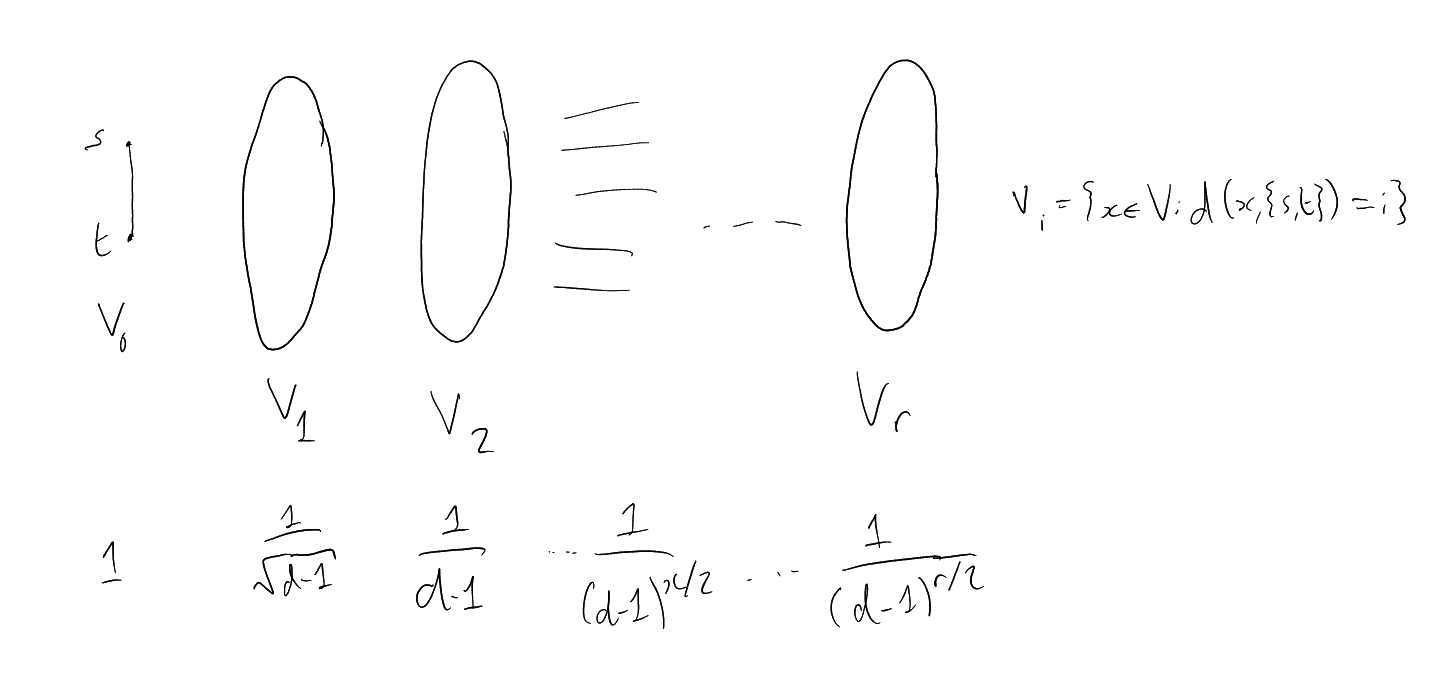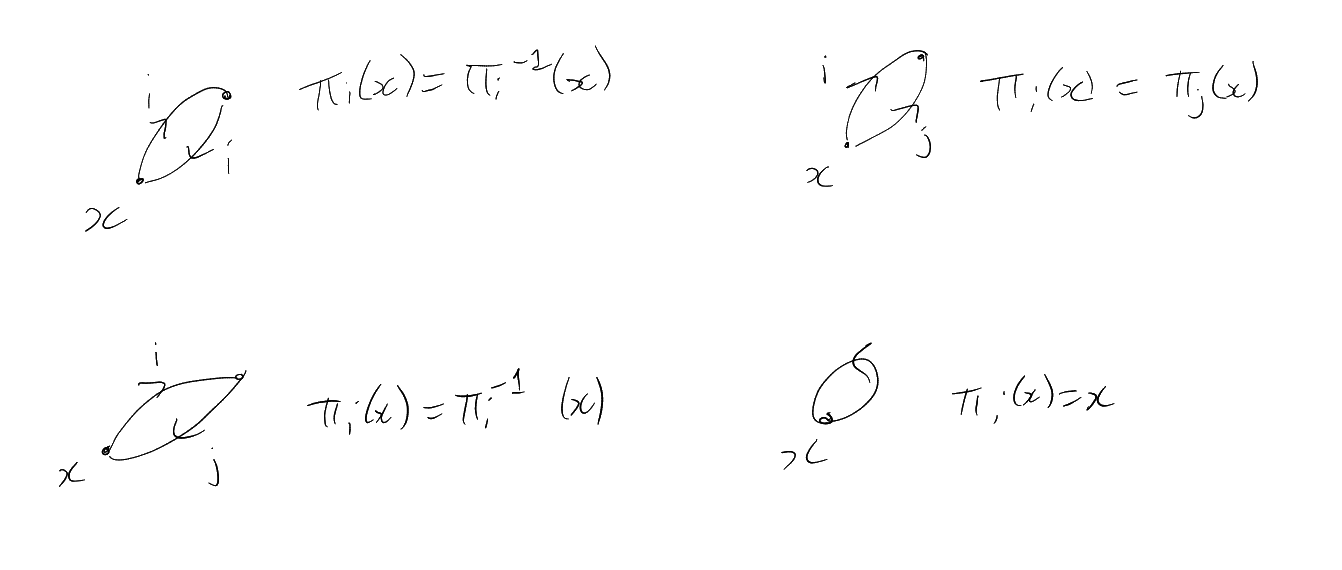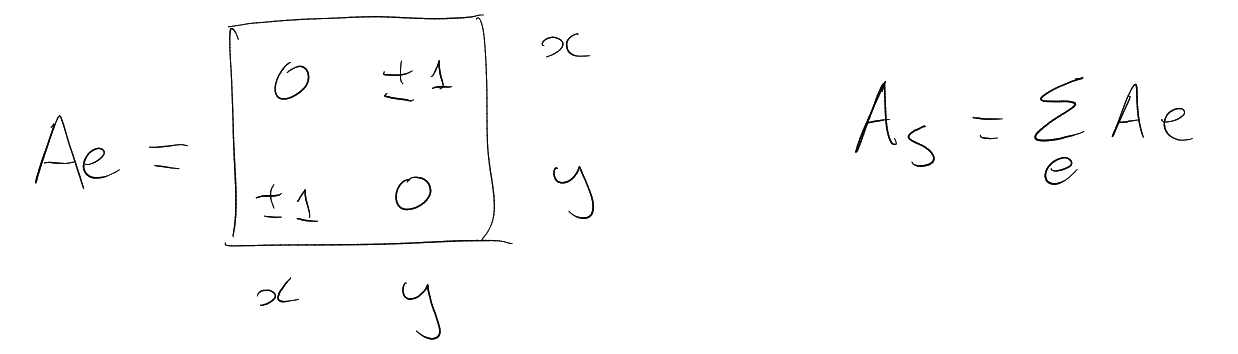4 Loewner order
Definition 4.1 (Loewner order).
For ,
matrices, write
if
is positive semidefinite. In particular,
if and only if
is positive semidefinite.
.
if and
only if ,
.
This is indeed an order:
implies
If , then
.
|
|
if and
only if .
If is a graph,
then .
Definition 4.2 (eps-approximation).
is an -approximation
of if
Lemma 4.3.
Given the definition
(for symmetric),
we have .
Proof.
,
,
,
|
|
|
|
Proof.
.
.
□
Definition ((d,eps)-expander).
,
is a -expander
if
is an -approximation
of .
Equivalent:
|
|
, where
is the all ones
matrix (). If
, then
. In this
case, .
So for
.
|
|
|
|
|
|
For ,
.
So is a
-expander if
and only if
for all .
Lemma 4.5 (Expander Mixing Lemma).
Assuming that:
Then ,
|
|
Proposition 4.6.
Assuming that:
Then the following are equivalent:
-
(i)
is a -graph
-
(ii)
,
for
-
(iii)
for
-
(iv)
for
-
(v)
-
(vi)
is -expander
(also -expander)
-
(vii)
-
(viii)
Lemma 4.7 (Expander Mixing Lemma).
Assuming that:
Then
Proof.
𝟙𝟙𝟙𝟙,
𝟙𝟙.
𝟙𝟙𝟙𝟙𝟙
.
|
𝟙𝟙𝟙𝟙 |
𝟙𝟙𝟙𝟙𝟙𝟙𝟙𝟙
To get the better bound, we should consider functions which are perpendicular to
: balanced
function
𝟙.
𝟙𝟙.
So
|
|
If is an
-graph
and an
independent set, then
|
|
.
Hoffman bound: .
Fix . How small can
be such that there
is an infinite family
of -graphs?
Note
has in
each entry of the diagonal, so
|
|
So .
So , so
|
|
as
.
Alon-Boppana Theorem: .
Claim: There exist families of -graphs
with .
They are called Ramanujan graphs. We will probably not prove existence of these.
Call -Ramanujan
if .
Theorem 4.8 (Friedman).
Assuming: - ,
Then:
|
|
Maxcut in -graph:
Diameter, vertex expansion. ,
.
|
|
.
Exercise: Diameter .
Vertex expansion
-graph
. Have
for all ,
|
|
.
If
,
,
then
,
,
fixed.
,
.
for
some .
Hence
if .
(by
considering ball around start and end).
Why aren’t Cayley graphs of abelian groups expanders?
Let be an abelian
group and a set of
generators of size .
Let .
Let .
Then
This is not exponential in ,
so the Cayley graph can’t be an expander.
Theorem 4.9 (Alon-Boppana).
Assuming that:
Proof 1.
Pick edge ,
pick .
,
|
|
|
|
.
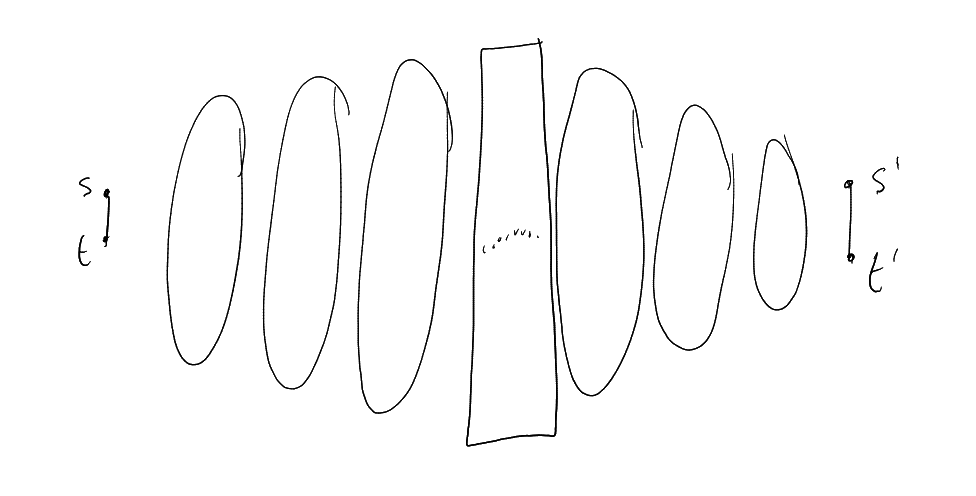
Suppose has 2
deges at distance .
,
as
above. .
|
|
Let .
Corollary 4.10.
For all ,
there are finitely many -graphs
with .
.
|
|
For Alon-Boppana:
Proof 2.
.
Note that
|
|
is at least
|
|
( is an infinite
-regular
tree). The latter is at least
|
|
Exercise: finish details. □
4.1 One-sided expanders
Goal is to find:
graphs with
vertices, -regular
such that .
Reminder: (Friedman) If
uniform random -regular
graph then
|
|
|
|
Theorem 4.11.
Assuming that:
Then there is
such
that there are
-regular
graphs (or multi-graphs)
on
vertices
with
for all
sufficiently large
.
Graphs
are as follows:
Lemma 4.12.
There is
such that
|
|
Lemma 4.13.
If
is -regular, then
there exists
such that
Proof.
If then
there exists ,
, there
exists ,
and
and
,
.
|
|
.
|
|
Fact 1:
if .
Proof: It is equivalent to
|
|
Compare the product term by term.
Fact 2: .
Proof:
Using these:
|
|
So
Decompose as .
Choose small
so that is
small. Choose
large so that .
Now .
Now let , so
this is .
Also, term
goes to .
□
For the lemma about :
These are the bad things. Use Bonferroni inequalities (the partial sum of inclusion exclusion principle
inequalities).
-graph
: number of
vertices, -regular,
,
.
Ramanujan graph: -graph.
-
Petersen -graph.
-
Complete (bipartite),
big :(.
-
Paley ,
.
big :(.
Alon-Boppana: For every
fixed , there are
finitely many -graphs.
Bipartite: -graph,
vertices,
-regular,
for
.
Theorem 4.14 (Lubotsky-Phillips-Sanak / Margoulis).
Assuming that:
-
prime
-
-
arbitrarily large
Then there exists a -graph.
Goal:
Theorem 4.15 (Marcus, Spielman, Srivastava).
Assuming that:
Then there are -bipartite
graphs for arbitrarily large .
Strategy: Bilu and Linial. Lifts of graphs:
Definition 4.16 (2-lift).
A 2-lift of a graph
is a graph ĜÊ
with
(and no other vertices or edges).
Definition 4.17 (Signing).
is a signing of
if
|
|
and
(symmetric). So can think of
as a function .
𝟙.
𝟙. Have
,
.
Lemma 4.18.
The eigenvalues of Ĝ
are the eigenvalues of (old)
together with the eigenvalues of
(new).
Proof.
Let .
Then
|
Ĝ |
Let .
Now
|
Ĝ |
Conjecture 4.19 (Bilu, Linial).
If
is -regular, then there
exists a signing whose
eigenvalues are in .
Theorem 4.20 (Bilu, Linial).
Can find signings
with eigenvalues
satisfying .
Theorem 4.21 (Marcusm, Spielman, Srivastava).
Assuming that:
Then there exists a signing with eigenvalues
with .
Theorem 4.21 implies Theorem 4.15.
-
Start with .
-
Keep applying Theorem 4.21 to find signing.
-
Build lift with that signing.
-
2-lift of bipartite graph is bipartite.
-
Spectrum of adjacency matrix of bipartite graph is symmetric around .
□
Notation.
For ,
let be
the number of inversions.
Theorem 4.21: .
For :
,
.
where
is the number
of matchings of size
in
.
is the matching
polynomial of .
Heilman-Lieb-Godsil:
-
is real rooted for all .
-
If
has degree ,
then
has roots in .
Last time, when working on ,
we showed:
Theorem 4.22 (Godsil-Gutman, 80s).
|
|
where
|
|
where is the number
of matchings in
with
edges.
Fact: is
real rooted.
Theorem 4.23 (Heilman-Lieb, 72).
Assuming that:
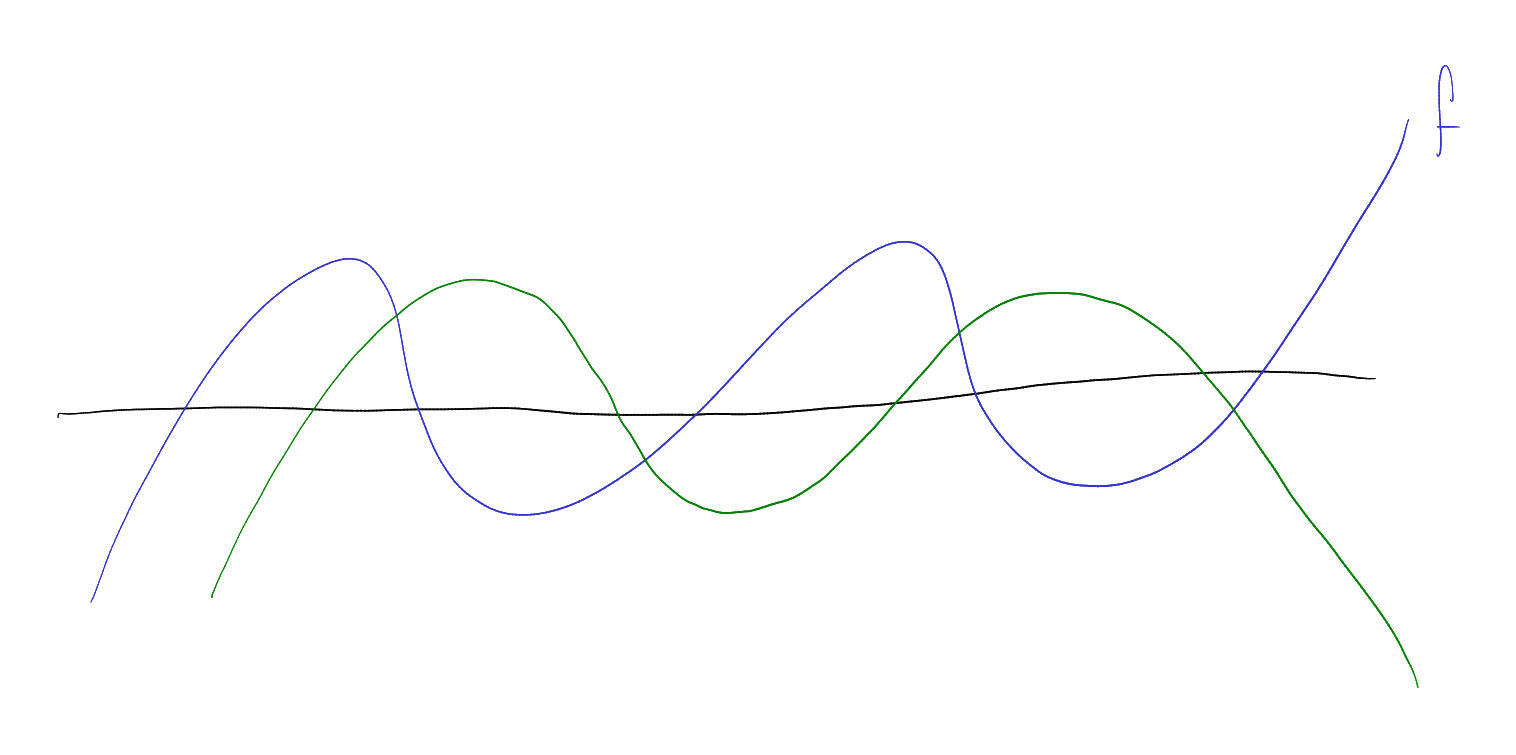
If only we could say that
is an average of ,
.
Hopelessly false:
Definition 4.24 (Interlacing).
Let
be a real rooted polynomial of degree
with roots and
a real rooted
polynomial of degree
with roots .
We say
interlaces if
|
|
Example.
If is real
rooted, then so is ,
and also
interlaces .
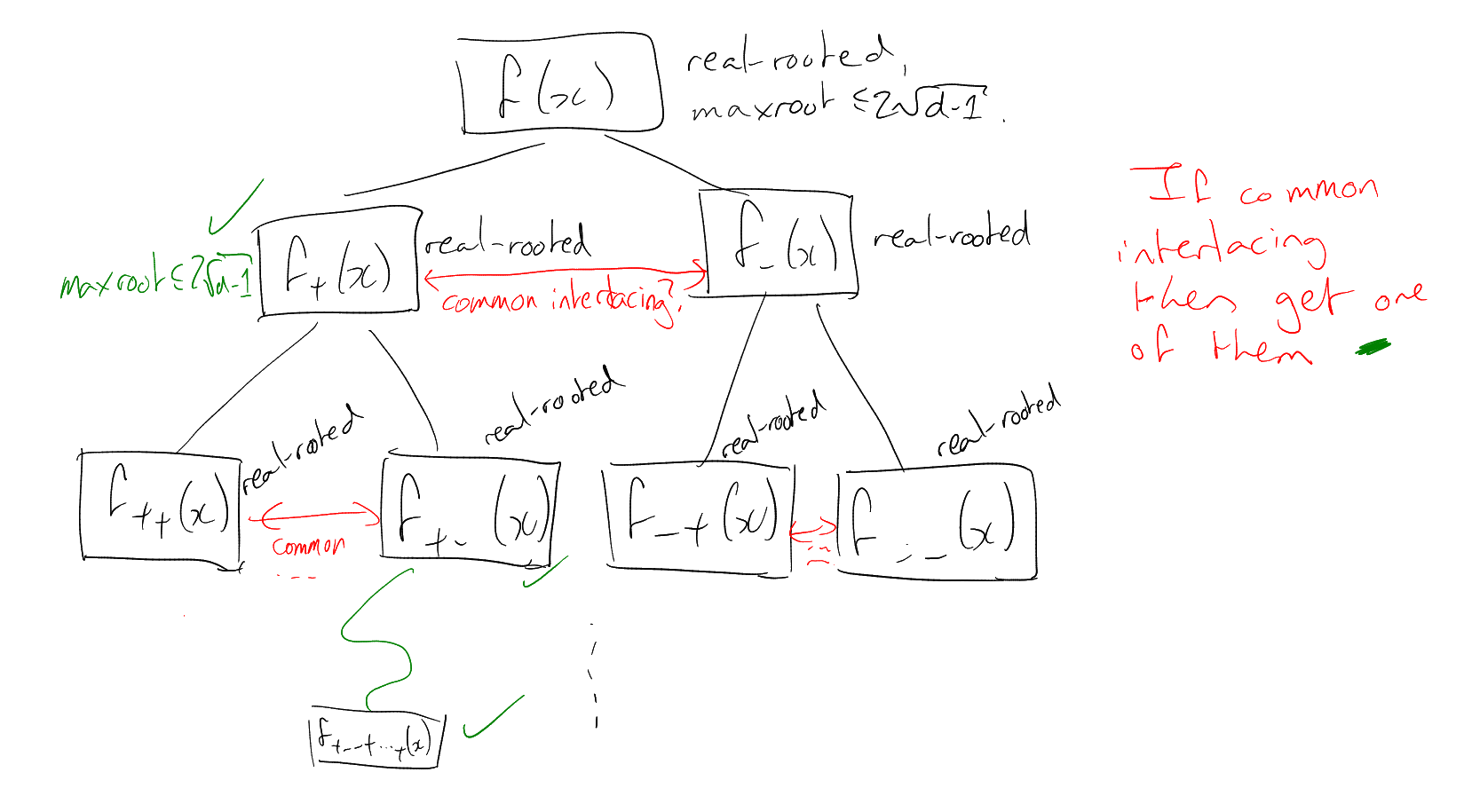
Definition 4.25 (Common interlacement).
We say that real rooted polynomials
,
of degree
have a common interlacement
if there is a polynomial
of degree such
that and
both interlace
. In other words,
if the roots of
and are
and
respectively, then they have a common interlacement if and only if there are some
such
that
|
|
Theorem 4.26 (Fell 80).
Assuming that:
-
,
are real rooted
-
both degree ,
monic
Then
and
have a common interlacing if and only if every convex combination of
and
are real
rooted.
Proof.
Assume
and
without repeated or common roots (general case requires more work and details checking).
-
Let
for .
We know these are real rooted, and waht to show that ,
have a common interlacement. Let
be the -th
root of .
includes .
Claim:
are disjoint.
Suppose not. Let
be a root of
and . So
there exists
such that .
|
|
so ,
contradiction as we assumed no common roots.
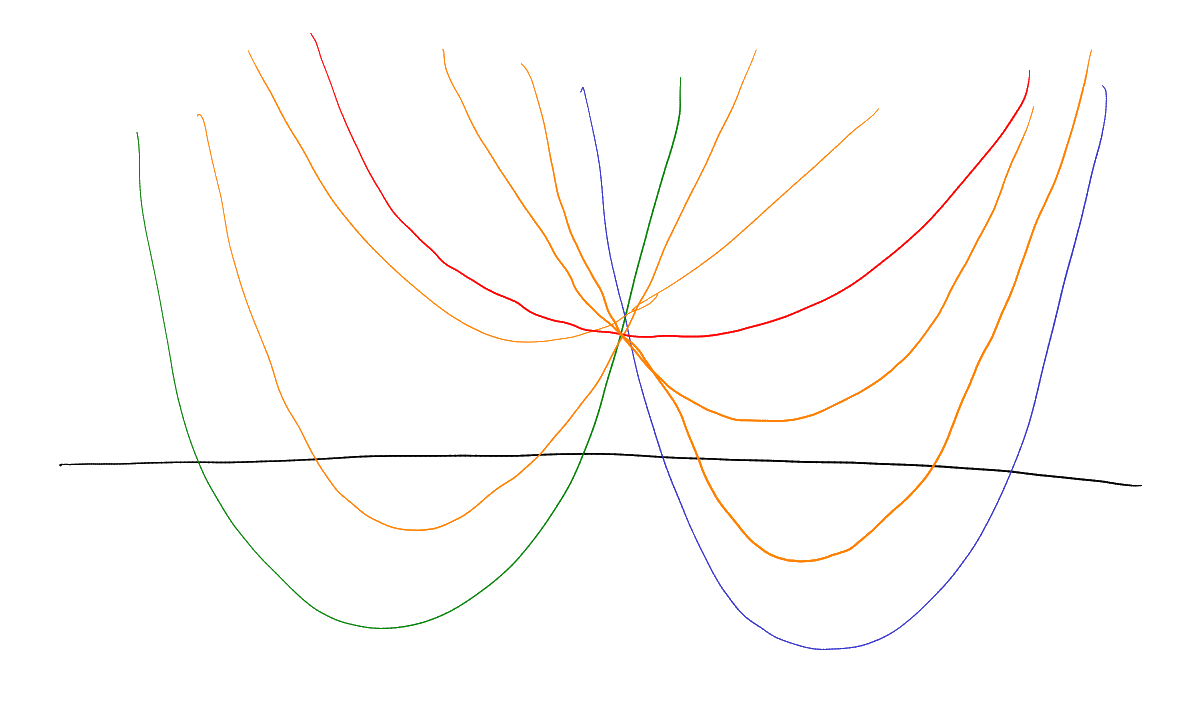
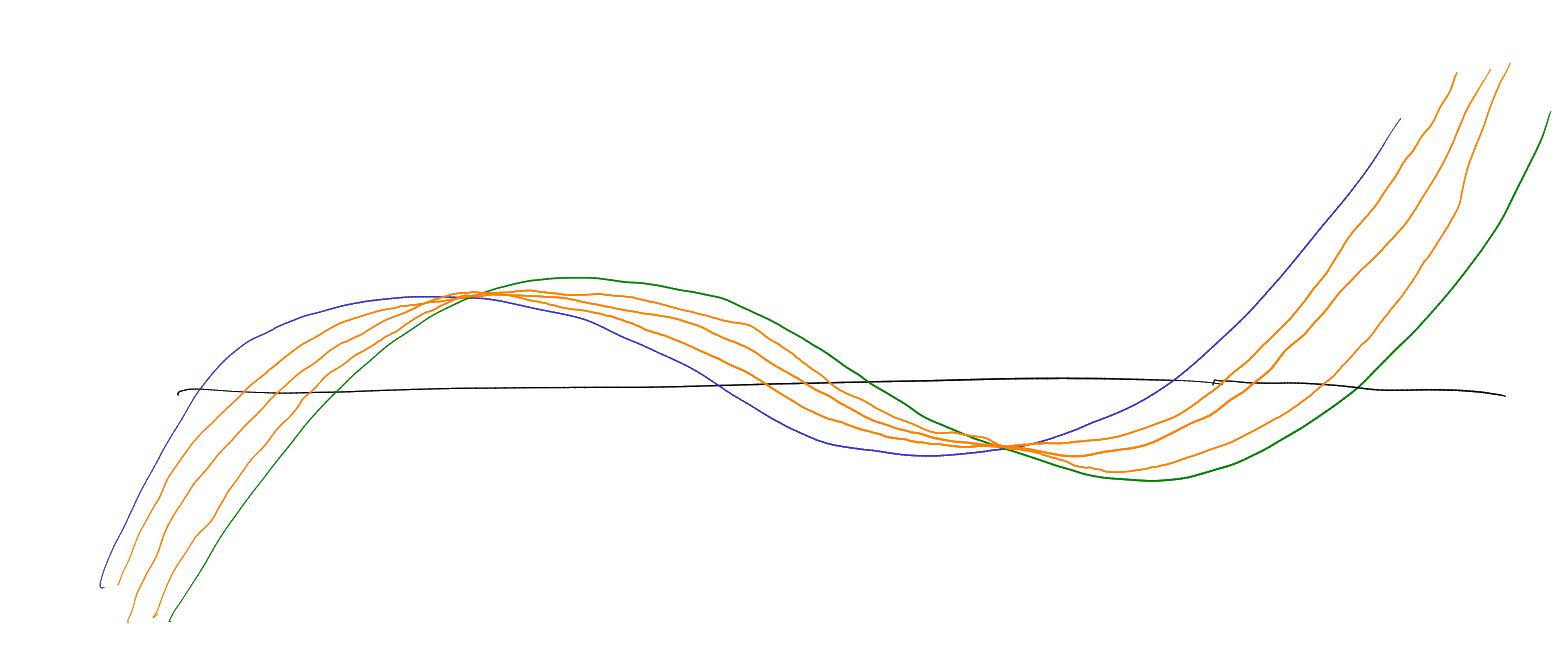
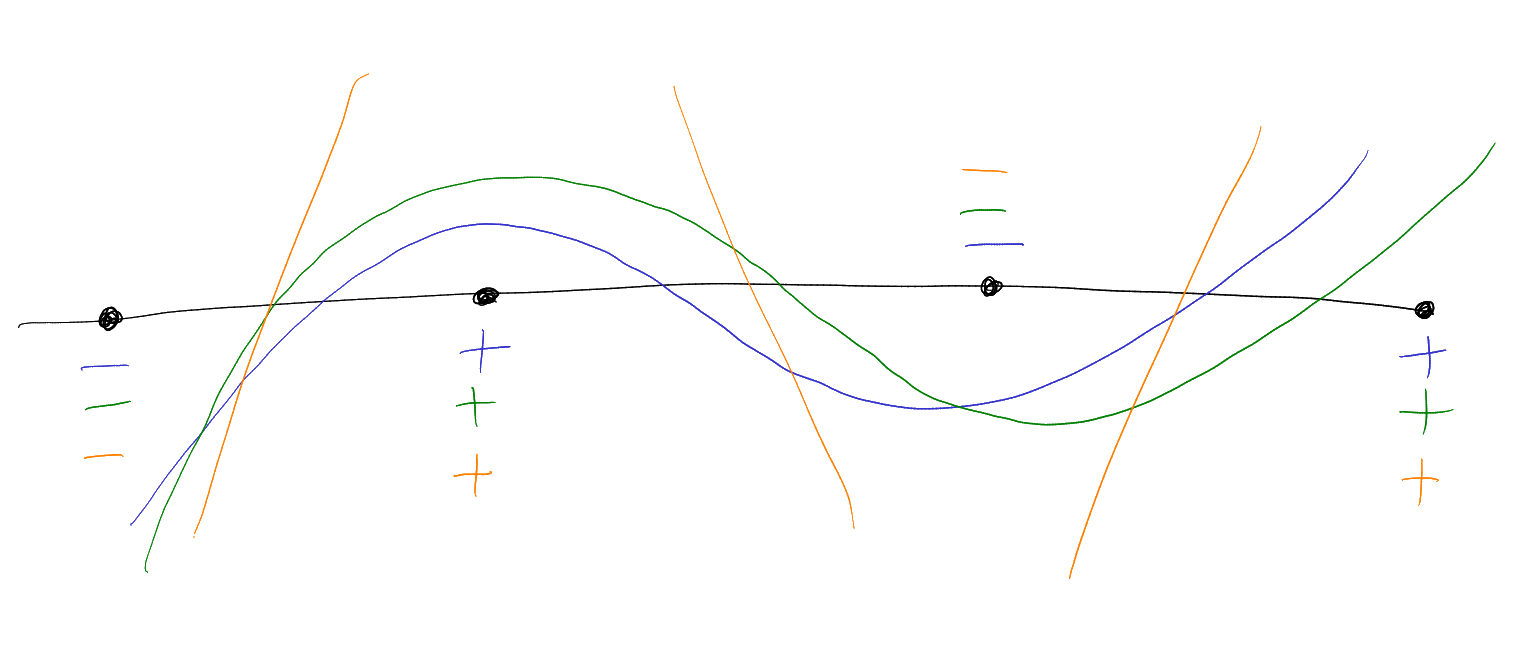
-
The dots represent the roots of the polynomial that interlaces them. By monicness, we get the blue and green
s and
s.
Then get the orange ones, and use intermediate value theorem. □
Corollary 4.27.
Assuming that:
Then for all
|
|
Approach to Theorem 4.21:
,
. For
, then
|
|
“Method of interlacing families of polynomials”
Theorem 4.28 (Marcus, Spielman, Srivastava (real rooted)).
For every
the
following polynomial is real rooted
|
|
Theorem 4.28 implies Theorem 4.21:
|
|
|
|
Theorem 4.29 (Marcus, Spielman, Srivastava (matrix)).
Assuming that:
Theorem 4.29 implies Theorem 4.28:
is
is real rooted
if and only if
is real rooted. This equals
Note
|
|
Done.
Definition 4.30 (Real stable).
A polynomial
is real stable if
for all ,
.
Notice that for a single variable,
is real stable if and only if real rooted.
Proposition 4.31 (Stable iff real rooted).
is real stable if and only if for all ,
, the
polynomial
is real rooted.
Proof.
-
If
not stable, then there exists
with ,
,
.
Then ,
.
-
Suppose ,
,
with
. Assume
.
.
.
□
Proposition 4.32 (Stability of real stable).
Assuming that:
Then the following are also:
-
,
.
-
,
.
-
.
-
,
.
-
.
-
.
-
.
.
-
If
are real stable, then so is .
Proposition 4.33 (Mother of all stable polynomials).
Assuming that:
Then is
real stable.
Proof.
Let ,
.
Assume positive definite instead of positive semi definite.
is positive
definite, and
is symmetric. So
The roots are eigenvalues of a real symmetric matrix, hence real. □
Proof of Theorem 4.29.
Say
equals with
probability , and
equals with
probability .
We will use Cauchy Binet:
|
|
|
|
is real stable since
is a covariance matrix.
So the earlier thing is real stable. So
is real stable. So
|
|
is real stable. Take ,
. Then
is real stable. □
Theorem 4.34 (Godsil).
Assuming that:
Then
where is the number of
closed walks of length
from in the
path tree of
.
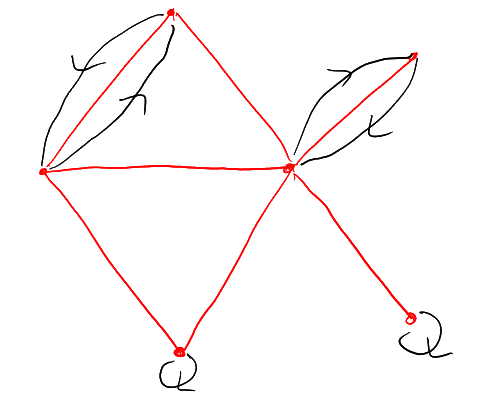
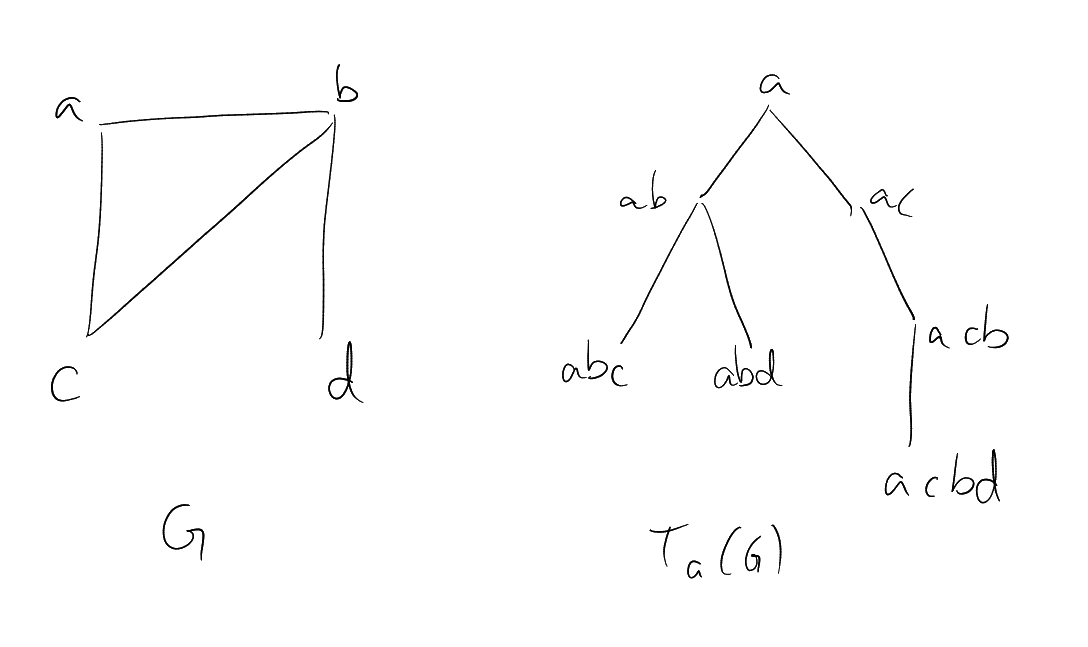
Definition 4.35 (Path tree).
Example:
Proof of ?? implies Theorem 4.23.
.
.
.
Take .
□
Proof of ??.
Hence
Claim:
.
Why? A tree-like walk in
that visits
exactly
times is determined by:
-
A sequence
of neighbours of .
-
A sequence
of walks in
where .
□